Способ контроля шероховатости поверхности изделия

Способ контроля шероховатости поверхности изделия

Иллюстрации

Показать все

Реферат

Изобретение относится к области измерительной техники, а именно к способам и устройствам для контроля шероховатости поверхности изделия, и может быть использовано в машиностроении, энергетике, авиации и других областях техники.

Известен способ контроля шероховатости поверхности сравнением с образцовой деталью и рабочими образцами шероховатости поверхности [1]. Сравнение исследуемой поверхности с образцами шероховатости поверхности выполняют органолептически, то есть по зрительному и осязательному ощущениям. На основании этого сравнения эксперт дает заключение о соответствии или несоответствии испытуемой поверхности установленным образцам. Образцы шероховатости поверхности (ГОСТ 9378-60) изготавливают для различных видов обработки (точения, растачивания, фрезерования, строгания, шлифования и т.д.) из стали, чугуна и металлизированных неметаллических материалов (позитивные реплики). При этом шероховатость образцовой поверхности определятся по известным методикам согласно ГОСТ 2789-73 "Шероховатость поверхности: параметры, характеристики, обозначения", например по профилограммам, снятым с помощью профилографа. Для сравнения применяют также и образцовые детали, аттестуемые с помощью стандартных приборов [1] по верхней и нижней границам допустимых значений стандартизированных параметров шероховатости поверхности.

Основным недостатком данного способа, как показывает производственный опыт и лабораторные наблюдения, является то, что заключения эксперта являются правильными, если к оценке предъявляются сравнительно грубые требования: например, требуется установить, что по высотным параметрам образцовая и исследуемая поверхности отличаются не более чем в два раза. При этом предполагается, что эксперт обладает достаточным навыком. В противном случае оценка становится еще более грубой, и вероятность ошибочных заключений возрастает. Кроме того, использование эксперта для проведения оценки требует определенных временных затрат и не позволяет автоматизировать процесс измерения шероховатости поверхности изделия непосредственно на этапе его изготовления.

В качестве прототипа принят способ измерения параметров шероховатости, основанный на цифровой обработке изображения исследуемой поверхности, введенного при помощи сканера или видеокамеры в ЭВМ [2]. В этом способе предлагается с помощью пакета прикладных программ в среде MathCad 2000 определять стандартные параметры шероховатости поверхности по изображению этой поверхности. При этом в качестве высотной характеристики микрорельефа поверхности принимается яркость (интенсивность) изображения этой поверхности в данной точке.

К недостаткам известного способа можно отнести:

1) невысокое быстродействие, так как по исходному полутоновому изображению непосредственно вычисляются стандартные параметры шероховатости;

2) необходимо использовать источник излучения, когерентный как во времени, так и в пространстве, что накладывает определенные ограничения на применение данного способа;

3) в качестве высотной характеристики исследуемого рельефа поверхности принимается яркость (интенсивность) изображения в данной точке, то есть амплитуда видеосигнала. Однако на интенсивность отраженного светового потока, попадающего в поле зрения объектива видеокамеры, значительное влияние может оказывать не только рельеф поверхности, но и общий уровень освещенности в помещении, стабильность источника освещения, угол наклона падающего светового потока на исследуемую поверхность, перпендикулярность оптической оси объектива исследуемой поверхности, различные блики от посторонних источников освещения, что существенно может исказить получаемые результаты. Кроме того, из радиотехники известно, что амплитудная модуляция из всех известных обладает наименьшей помехоустойчивостью.

Техническим результатом изобретения является повышение быстродействия и независимость получаемых результатов от интенсивности, жестких требований к стабильности, когерентности источника падающего светового потока, угла его падения на исследуемую поверхность и перпендикулярности оптической оси объектива исследуемой поверхности в широких диапазонах их изменения.

Технический результат достигается тем, что по предложенному способу исходное полутоновое изображение вначале преобразуется в бинарное, затем по бинарному изображению вычисляют двумерную автокорреляционную функцию, для которой после этого определяют среднее значение амплитуды переменной составляющей и для заданной вероятности определяют доверительный интервал, в который попадает средняя величина амплитуды переменной составляющей и, следовательно, максимальное и минимальное ее значения, затем по найденным значениям амплитуд переменной составляющей автокорреляционной функции, с использованием предварительно найденной зависимости среднего арифметического отклонения профиля от амплитуды переменной составляющей автокорреляционной функции для образцовых поверхностей, находят среднее значение арифметического отклонения профиля, а также минимальное и максимальное его значения с заданной вероятностью их определения.

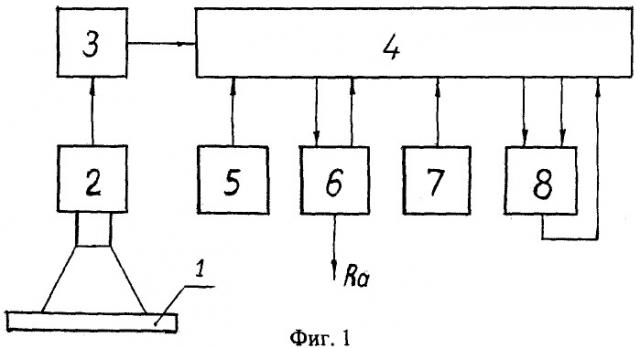
Сущность предложенного способа определения шероховатости поверхности раскрывает следующее устройство, принцип действия которого поясняется фигурой 1, где 1 - исследуемая поверхность, 2 - телевизионная передающая камера с ПЗС-матрицей, 3 - аналогово-цифровой преобразователь, 4 - запоминающее устройство, 5 - устройство для задания координат окна и его размеров для преобразования исходного полутонового изображения поверхности в бинарное, а также для задания размеров эталона в бинарном изображении, 6 - цифровое вычислительное устройство, 7 - устройство для задания координат текущего фрагмента бинарного изображения, 8 - коррелятор.

Определение шероховатости исследуемой поверхности по предложенному способу осуществляется следующим способом.

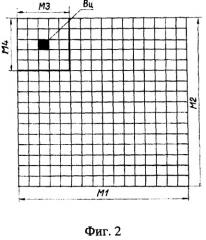
Вначале участок размером L1×L2 исследуемой поверхности 1 считывают по строкам и столбцам строчно-кадровым растром, например, телевизионной передающей камерой с ПЗС-матрицей 2. ТВ-камера матричного типа преобразует оптические сигналы с поля зрения в электрические видеосигналы. С помощью аналогово-цифрового преобразователя 4 видеосигналы переводятся в цифровые дискретные значения и записываются в запоминающее устройство 4. Таким образом, в запоминающем устройстве будет сформирован кадр исходного изображения анализируемой поверхности формата M1×M2 точек дискретизации - пикселей. Далее, с помощью устройства 5 в исходном полутоновом кадре, начиная с левого верхнего угла, задаются размеры окна преобразования M3×M4 пикселя - фиг.2. Этот фрагмент исходного изображения поступает в цифровое вычислительное устройство 6, где вычисляется средний уровень яркости в окне В_ср, а затем центральный элемент окна В_ц преобразуется по правилу: В_ц=1, если В_ц≥В_ср и В_ц=0, если В_ц<В_ср. Новое значение В_ц заносится в запоминающее устройство. После этого окно в исходном изображении с помощью устройства 5 смещается на один пиксель по горизонтали (можно по вертикали), также поступает в устройство 6 и выполняются те же самые действия. Таким окном сканируется весь кадр исходного изображения и в результате такой обработки в запоминающем устройстве будет сформирован бинарный кадр изображения исследуемой поверхности формата M5×M6, представляющий из себя матрицу, состоящую только из 0 и 1. Размеры матрицы определяются из соотношений: M5=M1-M3+1, M6=M2-M4+1.

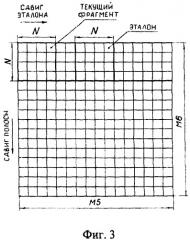
Для вычисления двумерной автокорреляционной функции в бинарном изображении с помощью устройства 5, начиная с первой строки, выделяется полоса шириной в N пикселей и по центру этой полосы задается эталон размером N×N пикселей. Этот эталон записывается в отдельную область запоминающего устройства 4. Затем с помощью устройства 7 эталон и выделенная полоса, начиная с крайней левой позиции - фиг.3, поступают в устройство 8 - коррелятор. Устройство 7 обеспечивает также перемещение эталона по выделенной полосе с шагом в 1 пиксель. При каждом совмещении эталона и текущего фрагмента бинарного изображения в корреляторе подсчитывается количество совпавших по своему значению одноименных пикселей между ними. Этой сумме придается смысловое значение коэффициента автокорреляции. Для получения нормированного значения коэффициента автокорреляции К полученная сумма делится на площадь эталона, то есть на S=N×N пикселей. Найденные значения К также сохраняются в запоминающем устройстве 4. Закончив вычисление коэффициентов автокорреляции в первой полосе, задается с помощью устройства 7 следующая полоса в бинарном изображении того же формата, что и предыдущая, но смещенная вниз на один пиксель. В этой полосе по центру задается новый эталон, но с теми же размерами, что и предыдущий, и выполняются те же самые действия для вычисления коэффициента автокорреляции и т.д. Таким образом, обработав весь бинарный кадр по отмеченной методике, в запоминающем устройстве будет сформирована матрица размерностью M7×M8 коэффициентов автокорреляции или двумерная дискретная автокорреляционная функция. При этом размеры матрицы определяются из соотношений M7=M5-N+1 и M8=M6-N+1. После этого найденные значения коэффициентов автокорреляции поступают в цифровое вычислительное устройство 6 для дальнейшей обработки. Для введения количественной оценки, на основании которой можно с заданной вероятностью надежно распознать оптико-электронным методом неизвестную шероховатость исследуемой поверхности, в предлагаемом способе используются следующие вычисления. В автокорреляционной матрице определяется среднее значение коэффициента автокорреляции К_ср. Затем из каждого элемента автокорреляционной матрицы вычитается найденное значение К_ср и подсчитывается сумма всех разностей по абсолютной величине. Затем эта сумма делится на размер автокорреляционной матрицы D=M7×M8:

Полученной таким образом оценке U можно придать смысловое значение средней амплитуды переменной составляющей двумерной автокорреляционной функции. По вычисленному значению U с заданной вероятностью P определяют доверительный интервал I_β, в который попадает эта случайная величина и, следовательно, минимальное U_min и максимальное U_max ее значения. После этого с использованием найденных значений U, U_min и U_max определяется шероховатость исследуемой поверхности, например параметр Ra, мкм, то есть среднее арифметическое отклонение профиля от средней линии согласно ГОСТ 2789-73 "Шероховатость поверхности". При этом для образцовых поверхностей с известными значениями шероховатости, которые определяются известными стандартными методами, например с помощью профилографа, предварительно по рассмотренной выше методике вычисляются зависимости Ra=f(U) и I_β=f(U) и заносятся в память цифрового вычислительного устройства. Используя зависимость Ra=f(U), определяют среднее арифметическое отклонение профиля Ra, мкм, исследуемой поверхности, а также минимальное и максимальное его значения для заданной вероятности определения случайной величины U.

В качестве примера рассмотрим использование данного способа для определения шероховатости цилиндрической поверхности бомбинированного ролика подшипника ступицы колеса автомобиля ВАЗ. Внешний вид ролика приведен на фиг.4. Для ролика режим шлифования был следующий: скорость абразивного круга 50 м/с, скорость ведущего круга 70 м/с, снимаемый припуск 0,01 мм, скорость продольной подачи 300 м/мин, работа с охлаждением и периодической правкой алмазным карандашом.

Для исследования были изготовлены методом бесцентрового шлифования на станке СВА АКМ 25/1 абразивными кругами на вулканитовой основе три образца из стали ШХ15 с различной шероховатостью поверхности. Исследуемые образцы были изготовлены на том же оборудовании и по той же технологии, что и ролик. Для этих же образцов на профилографе модели SJ-201P были записаны профилограммы и определены стандартные параметры шероховатости: образец №1 имел Ra=0,56 мкм, образец №2 - Ra=0,13 мкм и образец №3 - Ra=0,084 мкм. Найденные значения среднего арифметического отклонения профиля представляют собой средние значения, вычисленные по 10 измерениям для каждого образца.

Оптико-электронная система комплекса (фиг.1.) была настроена таким образом, что анализируемая поверхность эталонных образцов имела размер 3×2,5 мм. Формат видеокадра, записываемого в запоминающее устройство, составлял 320×240 пикселей. Видеоизображения этих поверхностей приведены на фиг.5.

Характерные изменения уровня яркости по строке видеокадра поверхностей исследуемых образцов приведены на фиг.6.

На фиг.7 приведены бинарные изображения поверхностей исследуемых образцов. Средний уровень яркости видеосигнала для преобразования исходного изображения подсчитывался в окне 21×21 пиксель.

После обработки всего бинарного кадра для исследуемых образцов получались двумерные автокорреляционные поверхности, характерный вид которых при размере эталона 64×64 пикселя приведен на фиг.8. Характерные изменения нормированных корреляционных сигналов приведены на фиг.9.

Из приведенных зависимостей видно, что с увеличением шероховатости увеличивается частота колебаний автокорреляционной функции и увеличивается доля регулярной составляющей. При этом для поверхности с наилучшей шероховатостью (образец №3) наблюдается резкое падение амплитуды корреляционного сигнала от места взятия эталона.

Выполнив рассмотренные в предлагаемом способе вычисления для нахождения средней амплитуды U переменной составляющей автокорреляционной функции для различных размеров эталонов, были получены результаты, приведенные в табл.1.

Таблица 1
Зависимость средней амплитуды переменной составляющей автокорреляционной функции от размера эталона
Ra, мкм	Средняя амплитуда U
Эталон 2×2	Эталон 4×4	Эталон 8×8	Эталон 16×16	Эталон 32×32	Эталон 64×64
0,084	U=70,8	U=44,8	U=26,9	U=15,9	U=9,6	U=6,1
σ=3,6	σ=2,1	σ=1,4	σ=1,2	σ=1,1	σ=0,8
0,13	U=76,2	U=54,3	U=37,1	U=24,2	U=16,3	U=11,4
σ=8,4	σ=5,6	σ=4,8	σ=3,7	σ=2,8	σ=2,7
0,56	U=79,6	U=56,0	U=38,1	U=26,7	U=21,0	U=17,2
σ=9,8	σ=6,4	σ=5,1	σ=4,6	σ=3,5	σ=3,2

Анализ приведенных данных показывает существенное влияние размера эталона как на среднюю амплитуду переменной составляющей автокорреляционной функции (АКФ), так и на ее среднеквадратичное отклонение (СКО). При этом наилучшее различие по амплитуде и СКО для образцов с различной шероховатостью наблюдается при использовании эталона размером 64×64 пикселя. Для этого случая на фиг.10 приведен график зависимости среднего арифметического отклонения профиля исследуемых поверхностей от средней амплитуды переменной составляющей АКФ.

Как видно из приведенного графика, с увеличением среднего арифметического отклонения профиля от средней линии возрастает и средняя амплитуда переменной составляющей в автокорреляционной функции. Для получения аналитической зависимости Ra=f(U) в данной работе был использован интерполяционный метод Лагранжа [2], который позволил получить уравнение для Ra в виде:

Для определения доверительных интервалов I_β, в которые попадает случайная величина U, зададим вероятность распознавания шероховатости поверхности равной P=0,99. Проведенными исследованиями было установлено, что образец №1 имел среднеквадратичное отклонение от U, равное σ=3,2, образец №2 - σ=2,7 и образец №3 - σ=0,8 (см. табл.1), а сама случайная величина U подчиняется нормальному закону распределения. В этом случае число среднеквадратичных отклонений t_β, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания случайной величины U в полученный интервал была P=0,99, имеет значение 2,576 [3]. Для каждого образца было обработано по 30 изображений с различных участков исследуемой поверхности, т.е. n=30. Тогда среднеквадратичное отклонение оценки для U определяется по формуле [3]:

Следовательно, для образца №1 имеем σ_T=0,58, для образца №2 - σ_T=0,49 и для образца №3 - σ_T=0,15. Через величины t_β и σ_T доверительный интервал выражается в виде:

Округляя вычисленные значения I_β·σ_T в сторону увеличения, получим:

для образца №1 - I_β=1,5,…15,7≤U≤18,7;

для образца №2 - I_β=1,3,…10,1≤U≤12,7;

для образца №3 - I_β=0,4,…5,7≤U≤6,5.

Как видно из приведенных данных, доверительные интервалы для U с увеличением шероховатости возрастают и, что очень важно, не перекрываются. График зависимости I_β=f(U) приведен на фиг.11. Как видно из приведенного графика, зависимость I_β=f(U) имеет нелинейный характер. Используя и в этом случае интерполяционный метод Лагранжа, получили для доверительного интервала аналитическое выражение в виде:

Таким образом, определяя с использованием оптико-электронного комплекса и рассмотренной выше методики определения средней амплитуды колебания переменной составляющей автокорреляционной функции U, можно с использованием аналитических зависимостей (1), (3) и (4) вычислять среднее арифметическое отклонение профиля исследуемой поверхности от средней линии, а также диапазон изменений Ra с заданной вероятностью их определения.

Бинарное изображение участка цилиндрической поверхности ролика - позиция "а", а также результаты преобразования этого изображения по рассмотренной выше методике - позиции "б" и "в", приведены на фиг.12.

В связи с тем, что цилиндрическая поверхность ролика из-за своей кривизны по-разному отображается в фокальной плоскости видеосистемы, для вычисления U был взят центральный участок поверхности размером 239×80 пикселей. Обработка 30 бинарных изображений автокорреляционных поверхностей дала значение U=7,32. Подставляя это значение в формулу (4), получаем I_β=0,66. Следовательно, U_min=6,66 и U_max=7,98. Используя найденные значения в формуле (1), получим: Ra=0,089 мкм, Ra_min=0,087 мкм и Ra_max=0,09 мкм. Найденные значения среднеарифметического отклонения профиля цилиндрической поверхности ролика вполне согласуются со значениями, определенными с помощью профилографа модели SJ-201P.

Используемая литература

1. Дунин-Барковский И.В., Карташова А.Н. Измерение и анализ шероховатости, волнистости и некруглости поверхности. М.: Машиностроение, 1987. - 232 с.

2. Яковлев А.В. Разработка параметров шероховатости поверхности, оцениваемых на плоскости по ее изображению / Методы и устройства передачи и обработки информации. Межвуз. сб. науч. тр. - Вып.3. / Под. ред. В.В.Ромашова, В.В.Булкина. - СПб.: Гидрометеоиздат, с.203-207, 2003.

3. Мышкис А.Д. Лекции по высшей математике. М.: Наука, 1969. - 640 с.

4. Вентцель Е.С. Теория вероятностей. М.: Наука, 1969. - 576 с.

Способ контроля шероховатости поверхности изделия, основанный на формировании исходного полутонового изображения исследуемой поверхности, отличающийся тем, что полутоновое изображение преобразуют в бинарное, затем по бинарному изображению вычисляют двумерную автокорреляционную функцию, для которой после этого определяют среднее значение амплитуды переменной составляющей автокорреляционной функции и для заданной вероятности определяют доверительный интервал, в который попадает средняя амплитуда переменной составляющей и по нему находят максимальное и минимальное ее значения, затем по найденным значениям амплитуды переменной составляющей автокорреляционной функции, с использованием предварительно найденной зависимости среднего арифметического отклонения профиля от амплитуды переменной составляющей автокорреляционной функции для образцовых поверхностей, находят среднее значение арифметического отклонения профиля для исследуемой поверхности, а также минимальное и максимальное его значения с заданной вероятностью их определения.