Способ тестопригодной реализации логических преобразователей

Способ тестопригодной реализации логических преобразователей

Иллюстрации

Показать все

Реферат

Изобретение относится к области автоматики и цифровой вычислительной техники и может быть использовано для создания сложных логических преобразователей (комбинационных автоматов) с высокой степенью готовности к динамическому функциональному тестированию при их электронном переключении из рабочего режима в режим тестирования как на этапе их производства, так и на этапе их эксплуатации.

Известен способ и вариант его технической реализации, обеспечивающий тестопригодность логических преобразователей, реализованных в виде двухуровневых программируемых логических матриц (ПЛМ), логическим базисом которых является основной элементный базис из логических элементов И, ИЛИ, НЕ [1].

ПЛМ содержит входной дешифратор «1→2», матрицу многовходовых элементов И, матрицу многовходовых элементов ИЛИ и дополнительные схемы, распределенные по узлам ПЛМ. Во входной дешифратор добавлены две линии управления; к столбцам матрицы И дополнительно подключаются выходы разрядов дополнительного регистра сдвига; в матрицу И и в матрицу ИЛИ дополнительно вводятся один столбец и одна строка соответственно для дополнения до нечетности подключений к каждой строке и каждому столбцу; к строкам и столбцам дополнительно подключаются наборы из элементов неравнозначности (сумма по модулю 2). Линии управления, которые подключаются к дешифраторам, используются для активизации какой-либо одной или одновременно всех строк матрицы И. Дополнительный регистр сдвига предназначен для активизации какого-либо одного столбца матрицы или всех столбцов одновременно. Если активизированы все строки матрицы и только один из столбцов, то проверяется правильность формирования i-го терма (i-й элементарной конъюнкции) путем проверки на нечетность числа переменных i-го терма дополнительным столбцом из последовательно включенных элементов неравнозначности. Если активизирована единственная строка матрицы и все ее столбцы, то проверяется на нечетность количество вхождений переменной данного типа в различные термы дополнительной строкой из последовательно соединенных элементов неравнозначности. Таким образом, данный способ тестирования двухуровневой ПЛМ заключается во введении такой структурной и функциональной избыточностей в двухуровневую ПЛМ, которая позволяет проводить последовательную проверку целостности структуры как незапрограммированной, так и запрограммированной ПЛМ путем предварительного обеспечения и последующего определения нечетности числа переменных в каждом терме (т.е. в каждом столбце матрицы) и нечетности вхождения каждой переменной в различные термы (т.е. в каждой строке матрицы), при этом реализуемая логическим преобразователем логическая функция исходно представляется и программируется в виде дизъюнктивной нормальной формы. Недостатками данного способа тестопригодной реализации логических преобразователей и устройств на его основе является невозможность проверки правильности функционирования логических преобразователей на предельных рабочих частотах, а также наличие значительного количества дополнительных узлов и коммутаций, приводящих к снижению общей надежности функционирования логических преобразователей.

Наиболее близким по технической сути является способ тестопригодной реализации логических преобразователей, описанный в [2].

Данный способ состоит в том, что он включает первоначальное получение исходного математического описания рабочего закона функционирования n-входовых логических преобразователей в тестопригодном логическом базисе Жегалкина, затем разработку и реализацию структурной схемы логического преобразователя из элемента генератор логической 1 (Gl), m k-местных логических элементов И (&) и последовательной цепочки из (m-1) элементов неравнозначности (⊕), определение в последующем количества и структуры n тестовых сигналов и структуры эталонного сигнала и их генерирование внешними техническими средствами.

Данный способ тестопригодной реализации логического преобразователя, базируется на том, что математическое описание в виде полинома Жегалкина (ПЖ) не содержит ортогональных конъюнкций. В этой связи представляется возможным все схемы, реализующие элементарные конъюнкции, параллельно и стандартно тестировать при помощи (n+1) тестовых наборов (один набор из всех 1 и n наборов «бегущий 0»). Все элементы, осуществляющие последовательную операцию ⊕, также тестируются стандартно с помощью четырех тестовых наборов, один из которых состоит из одних единиц, второй из всех нулей, третий из одного нуля и остальных единиц, а четвертый является инверсией третьего. Таким образом, данный способ тестопригодной реализации, позволяет тестировать логические преобразователи, реализующие логическую функцию от n аргументов и не содержащие неисправностей на входах, с помощью стандартных тестовых векторов, структура которых инвариантна к реализуемой логической функции [2, 3]. В том случае, если входные переменные входят в ПЖ четное число раз, то потребуется не более ((n+4)+n) тестовых наборов [3].

Недостатком данного способа тестопригодной реализации логических преобразователей является то, что, по сути, тестируется при минимальном количестве тестовых наборов неправильность реализации логической функции, а лишь исправность формирующей структуры и в предположении, что в логическом преобразователе могут возникать только одиночные и только константные неисправности. Иначе говоря, такой способ тестопригодной реализации ориентирован на готовность к оперативному статическому тестированию целостности структуры логического преобразователя минимальным количеством n разрядных тестовых наборов стандартной структуры, причем порядок следования этих наборов может быть произвольным. Вместе с этим эталонный сигнал, который может формироваться только с использованием внешнего запоминающего устройства, проверяет правильность функционирования логического преобразователя на ((n+4)+n) входных наборах, максимальное количество которых равно 2ⁿ. Для более эффективного динамического функционального тестирования произвольных логических преобразователей необходимо в псевдослучайном порядке и на предельно возможной частоте подавать на их входы все возможные 2ⁿ тестовых набора и одновременно с ними формировать соответствующий эталонный сигнал (т.е. реализовать исчерпывающее динамическое функциональное тестирование), что не обеспечивается при данном способе тестопригодной реализации логических преобразователей.

Изобретения направлено на повышение тестопригодности логических преобразователей для их динамического функционального тестирования на предельной рабочей частоте.

Это достигается тем, что k-местные операции логического умножения реализуют последовательно цепочками из (k-1) двухместных логических элементов с электронно перестраиваемой логической функцией, которые в рабочем режиме последовательно реализуют логическую функцию И над k аргументами, а в режиме тестирования последовательно реализуют логическую функцию равнозначности над теми же аргументами, после чего с помощью дополнительного внешнего сигнала управления организуют режим тестирования логического преобразователя n тестовыми М-последовательностями из одного и того же замкнутого класса и эталонной М-последовательностью, которую алгоритмически формируют из n тестовых М-последовательностей и одновременно с ними генерируют внешними техническими средствами на предельно возможной рабочей частоте логического преобразователя.

Для осуществления предлагаемого изобретения закон функционирования n-входового логического преобразователя исходно должен быть задан полиномом Жегалкина, общий вид которого может быть представлен следующим образом:

где x_i - i-я входная логическая переменная;

C_i - j-й коэффициент, указывающий на необходимость реализации соответствующей конъюнкции при C_j=1;

x_ix_f…x_s - некоторая конъюнкция логических переменных;

m=2ⁿ; Cj={0,1}, j=0,(2ⁿ-1); х_i={0,1}, i=1, n.

Сочетание переменных в правой части (1), например C_(m-1)x₁x₂…x_n, следует понимать как их логическое произведение, т.е.

C_(m-1)x₁x₂…x_n=C_(m-1)&x₁&x₂&…&x_n

В зависимости от того, какую именно логическую функцию должен реализовывать логический преобразователь, для выражения (1) должны быть предварительно определены значения соответствующих коэффициентов C_j, что может быть осуществлено широко известным методом неопределенных коэффициентов [4].

Рассмотрим осуществление заявляемого способа тестопригодной реализации логического преобразователя, закон функционирования которого изначально задается следующим полиномом Жегалкина:

Функции (2) соответствует такая логическая функция, которая принимает логическое значение, равное 1, только на одном единственном наборе значений логических переменных, когда каждая переменная равна логическому 0.

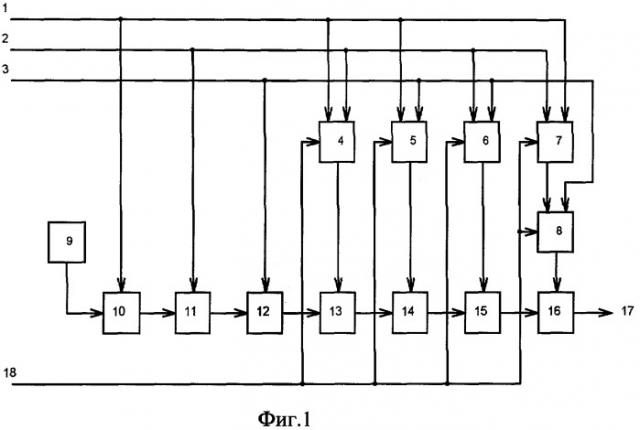
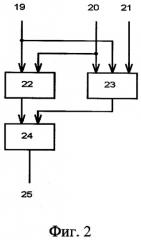
На фиг.1 представлена структурная схема тестопригодного логического преобразователя, которая разработана на основе выражения (2), а на фиг.2 - структурная схема логического элемента VAR с электронно перестраиваемой логической функцией.

Входные логические переменные x₁, x₂, x₃ подаются соответственно на входы логического преобразователя 1, 2, 3 и в соответствии с реализуемой логической функцией подключаются к первому 19 и/или к второму 20 входам элементов VAR 4, 5, 6, 7, 8. Выход элемента VAR 7 подключается к входу 19 элемента VAR 8, образуя таким образом их последовательную цепочку. На вход 18 поступает дополнительный сигнал управления u, который подключается к третьим входам 21 всех элементов 4, 5, 6, 7, 8. Первые входы элементов неравнозначности 10, 11, 12, 13, 14, 15, 16 соответственно соединены с первым, вторым, третьим входами логического преобразователя и выходами элементов 4, 5, 6, 8. Выходы элементов 10, 11, 12, 13, 14, 15 соответственно соединяются со вторыми входами элементов 11, 12, 13, 14, 15, 16. Выход элемента 16 соединен с выходом 17 логического преобразователя. Второй вход элемента 10 соединен с выходом элемента 9, реализующего логическую функцию генератора логической 1.

При u=1 реализуется рабочий режим функционирования логического преобразователя в соответствии с заданной логической функцией (в данном случае F(x₁,х₂,х₃)), что обеспечивается настройкой элементов 4, 5, 6, 7, 8 на последовательную реализацию конъюнкции переменных, поступающих на входы 19 и 20. При u=0 структура логического преобразователя реконфигурируется путем одновременной электронной перестройки элементов 4, 5, 6, 7, 8 на реализацию логической функции равнозначности (⊗) над логическими переменными, поступающими на входы 19 и 20. Логическое уравнение, задающее закон функционирования элементов 4, 5, 6, 7, 8 при поступлении на их входы 19 и 20 переменных a и b соответственно и на вход 21 сигнала управления u, имеет следующий вид:

где y - выходной сигнал, формируемый на выходах 25 элементов 4, 5, 6, 7, 8, в которых элемент 22 реализует логическую функцию И над входными сигналами a и b, элемент 23 реализует логическую функцию ИЛИ-НЕ над сигналами a и b, а также над сигналом управления u, а элемент 24 реализует функцию ИЛИ над сигналами с выходов элементов 22 и 23.

В результате настройки элементов 4, 5, 6, 7, 8 на реализацию функции равнозначности закон функционирования логического преобразователя задается уравнением, содержащим только операции неравнозначности и равнозначности. Такое уравнение получают из исходного математического описания путем формальной замены в нем всех операций логического И на операции равнозначности с последующим приведением их к операциям неравнозначности, что применительно к функции F(x₁,х₂,х₃), выражается следующим логическим уравнением:

Так как справедливы [4] следующие соотношения:

то соотношение (3) преобразуется к линейной функции, тождественно равной 0, т.е. F'(x₁,х₂,х₃)=0. В зависимости от реализуемой логической функции в рабочем режиме логический преобразователь в режиме тестирования (при отсутствии в нем неисправностей) реализует одну из возможных линейных логических функций, общий вид которых соответствует соотношению (5):

где коэффициенты В_i={0,1}, i=0,n; x_j={0,1}, j=1,n.

Коэффициенты B_i не вычисляются, они автоматически находятся из выражений вида (3) с использованием соотношений (4).

В режиме тестирования логического преобразователя переменные x_j (j=1,n) заменяются на псевдослучайные последовательности максимальной длины (M-последовательности), которые могут генерироваться на предельных частотах внешним n-разрядным регистром сдвига с линейной обратной связью [3]. Множество M всех M-последовательностей, генерируемых n-разрядным регистром сдвига, состоит из 2(2ⁿ-l) M-последовательностей, отличающихся друг от друга величиной циклического сдвига и/или инверсными значениями битовых сигналов. Тогда каждой М-последовательности можно присвоить номер, соответствующий ее циклическому сдвигу относительно какой-либо M-последовательности, произвольно выбранной за первую. Тогда M={M₁,M₂,…M_S}, S=2(2ⁿ-1). Специфической особенностью M_S из M является то, что для них выполняются все соотношения (3), а также и соотношение (4), при этом эталонная реакция М_Э правильно функционирующего логического преобразователя будет также принадлежать множеству M и может алгоритмически формироваться из n тестовых M-последовательностей, что обеспечивает возможность одновременного формирования тестовых и эталонной M-последовательностей на предельной рабочей частоте логического преобразователя. Как видно из структурной схемы, представленной на фиг.1, и соотношения (3), любая константная неисправность, кроме неисправностей на входах, будет искажать выходную функцию логического преобразователя в режиме тестирования M-последовательностями и, следовательно, будет обнаружена при несовпадении выходного сигнала логического преобразователя с M_Э. Предлагаемый способ тестопригодной реализации логических преобразователей также эффективен и для обнаружения неисправностей типа коротких замыканий. При коротких замыканиях проводников в цифровой схеме в точках замыкания реализуются над логическими (двоичными) сигналами так называемые монтажное И или монтажное ИЛИ. Если электрический сигнал логического 0 подавляет электрический сигнал логической 1, то реализуется монтажное И. Если электрический сигнал логической 1 подавляет электрический сигнал логического 0, то реализуется монтажное ИЛИ. С учетом этого, а также уникальной особенности M-последовательностей, заключающейся в том, что любые две различные M-последовательности из одного и того же класса отличаются в половине своих (2ⁿ-1) разрядов, следует, что любые неисправности типа коротких замыканий будут обнаруживаться, так как при возникновении монтажных И или ИЛИ выходная функция логического преобразователя будет отличной от M_Э. Достоверное тестирование по данному способу необходимо проводить путем сравнения эталонного тестового сигнала с реально формируемым на выходе логического преобразователя с запаздыванием, величина которого определяется как τ=rt_зп, где r - количество последовательно включенных элементов неравнозначности, a t_зп - время задержки их переключения.

Техническим результатом от использования заявляемого изобретения является повышение тестопригодности логических преобразователей, реализованных в элементном базисе Жегалкина, за счет обеспечения их готовности к динамическому функциональному тестированию на максимальной рабочей частоте, когда создаются наилучшие условия для проявления скрытых потенциальных константных неисправностей и неисправностей типа коротких замыканий между линиями электрических связей.

Источники информации

1. Киносита К., Асада К., Карацу О. Логическое проектирование СБИС.- М.: Мир.- 1988. 309 с.

2. Горяшко А.П. Синтез диагностируемых схем вычислительных устройств. - М.: Наука. 1987. - 288 с.

3. Ярмолик В.Н. Контроль и диагностика цифровых узлов ЭВМ. - Мн.: Наука и техника, 1988. - 240 с.

4. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. - М.: Физматлит, 2005. - 460 с.

Способ тестопригодной реализации логических преобразователей, включающий первоначальное получение исходного математического описания рабочего закона функционирования n-входовых логических преобразователей в тестопригодном логическом базисе Жегалкина, затем разработку и реализацию структурной схемы логического преобразователя из элемента генератор логической 1, k-разрядных логических элементов И, реализующих k-аргументные функции И, и последовательной цепочки из (m-1) элементов неравнозначности, определение в последующем количества и структуры n тестовых сигналов и структуры эталонного сигнала и их генерирование внешними техническими средствами, отличающийся тем, что с помощью дополнительного внешнего сигнала управления организуют рабочий режим работы и режим тестирования логического преобразователя, причем в рабочем режиме k-аргументные функции И реализуют последовательными цепочками из (k-1) двухвходовых логических элементов И, каждый из которых в режиме тестирования электронно и одновременно достраивают до двухразрядных логических элементов равнозначности, которые реализуют k-разрядные логические функции равнозначности над входными аргументами в качестве которых в режиме тестирования используют n тестовых М-последовательностей из одного и того же замкнутого класса, при этом эталонную М-последовательность алгоритмически формируют из n тестовых М-последовательностей, причем тестовые и эталонную М-последовательности одновременно генерируют внешним n-разрядным регистром сдвига с линейной обратной связью на предельно возможной рабочей частоте логического преобразователя.