Способ картографического отображения двумерных распределений, заданных в цифровой форме

Способ картографического отображения двумерных распределений, заданных в цифровой форме

Иллюстрации

Показать все

Реферат

Изобретение относится к области геодезии и картографии, в частности к картографическому моделированию при структурно-тектонических, геофизических, геохимических и т.п. исследованиях, при поисково-разведочных работах, инженерно-геологических изысканиях и т.д.

Известен оптический способ построения карт плотности распределения заданных графическим способом элементов (пятен, точек и линий) на исследуемой площади, включающий преобразование изображений дискретных графических распределений в непрерывную полутоновую форму с дальнейшим их представлением в форме изолиний - эксинденсит (Авторское свидетельство SU №365562, 1970 [1]).

Однако данный способ не предусматривает обработку данных, заданных в цифровой форме.

Известен также способ картографического отображения двумерных распределений, заданных в цифровой форме, включающий преобразование изображений дискретных графических распределений в непрерывную полутоновую форму с дальнейшим их представлением в форме изолиний - эксинденсит, в котором с целью повышения точности при оптическом моделировании кодируют цифровые значения признака в заданной точке планшета оптическими символами - разновеликими пятнами с оптической плотностью, пропорциональной величине признака (Авторское свидетельство SU №64011, 1978 [2]), что обеспечивает отображение двумерных распределений, заданных в цифровой форме.

Однако в большинстве случаев картографического отображения необходимо построение трехмерной модели рельефа, заданной в аналитическом виде при отображении результатов экологического состояния регионов (см., например, Патент RU №2079891, заявка №92007530 от 23.11.1992), результатов ситуационного мониторинга объектов хозяйственной деятельности, например морских газонефтяных месторождений и терминалов, включая подводные исследования с отображением рельефа местности, что известными способами не обеспечивается.

Известен также способ построения трехмерной модели рельефа в виде кусочных сплайн-функций двух переменных. Исходной информацией служит типографская карта местности. Способ реализуется посредством геопространственной информационной системы (ГИС) (Берлянт A.M. Картография. - М.: Аспект Пресс, 2002. - 336 с. [3]).

Эффективность аналитической обработки данных в геопространственных информационных системах в значительной степени зависит от возможностей, обеспечиваемых цифровой моделью рельефа (ЦМР), определяемой как совокупности высотных отметок, взятых в узлах некоторой регулярной или нерегулярной сети точек с заданными координатами [3]. В автоматизированных системах ЦМР служит основой получения прямой и косвенной информации о рельефе местности. Например, получение информации о морфометрических данных, включая вычисление углов наклона и экспозиции склонов; анализ видимости/невидимости; построение трехмерных изображений; профилей поперечного сечения; оценку формы склонов через кривизну их поперечного и продольного сечения; вычисление положительных и отрицательных объемов; генерацию линий сети тальвегов и водоразделов, образующих каркасную сеть рельефа, его структурных линий и иных особых точек рельефа: локальных минимумов (впадин) и локальных максимумов (вершин), седловин, бровок, линий обрывов и иных нарушений «гладкости» поверхности и т.д.

Источниками исходных данных для создания ЦМР, например, суши служат топографические карты, аэрофотоснимки, космические снимки, данные альтиметрических измерений, морские навигационные карты, данные промерных гидрографических работ. При этом принята следующая технология построения ЦМР (Суворов С.Г., Дворецкий Е.М., Коваленко С.А. Методика создания цифровых моделей рельефа повышенной точности // Информация и космос. №1, 2005 - с.52-54 [4]). Вся доступная информация оцифровывается. Полученные от разнообразных источников данные сводятся в единый набор координат точек и высот в них. Этот набор триангулируется (обычно методом Делоне). Процедура триангуляции дает систему непересекающихся треугольников, покрывающих рассматриваемую область поверхности земли (TIN-модель). В результате чего рельеф представляется многогранной (элементарная грань - треугольник) поверхностью с высотными отметками (отметками глубин) в узлах треугольной сети. Каждая грань этой поверхности описывается либо линейной функцией (полиэдральная модель), либо полиномиальной поверхностью, коэффициенты которой определяются по значениям в вершинах граней-треугольников. Эта технология в различных вариантах реализована во всех применяемых на практике ГИС.

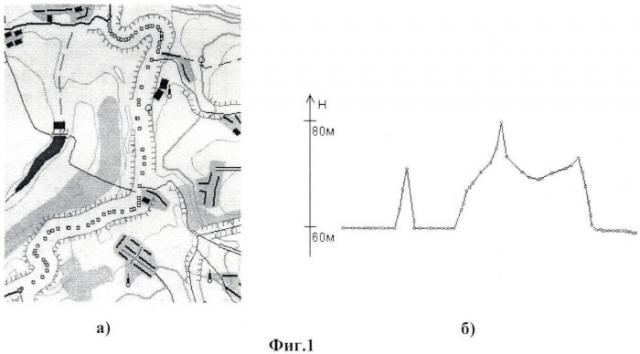
При этом цель построения ЦМР - получение адекватной прямой и косвенной информации о рельефе в автоматизированных системах - не достигается. Источником всех недостатков этой технологии является этап триангуляции. При этом рельеф представляется в виде непрерывной функции, но с разрывами уже в соответствующей функции первого дифференциала на ребрах триангуляции (т.е. негладкая функция). Это противоречит модели рельефа, которая принята при построении топографических или навигационных карт, где поверхность рельефа представляется гладкой функцией. Кроме того, истинное назначение триангуляции - это задать порядок (сеть) по степени близости и взаимному расположению на множестве точек в плоскости, следовательно, при этом не учитывается взаимоотношение высот (глубин) между точками, что приводит к искажению пространственного направления и смещению в местоположении структурных линий рельефа. К основным видам структурных линий рельефа относятся гребневые и килевые линии, линии выпуклого и вогнутого перегибов. Под гребневыми линиями, или водоразделами, понимают линии плановой корреляции точек с максимальными высотами. Килевые линии (тальвеги, русла) соединяют точки с минимальными высотами. Кроме того, результат триангуляции резко и непредсказуемо изменится при изменении исходного набора точек, т.е. при удалении, добавлении точки (точек) или при изменении координат в исходном массиве точек. Это свойство триангуляции не позволяет «управлять» (редактировать) построением локальной формы рельефа. Кроме того, если ЦМР при этом построена с использованием триангуляции, то результаты вычислений дифференциалов рельефа различных порядков не являются достоверными. Можно констатировать, что в этой области геоинформатики существует проблемная ситуация, выражающаяся в том, что технология построения ЦМР с использованием процедуры триангуляции не позволяет достичь требуемой цели. Этот вывод иллюстрируется на фиг.1. Из чертежа следует, что по данным построенной с помощью триангуляции ЦМР воды реки должны течь в гору.

Разрешить сложившуюся проблемную ситуацию можно путем применения таких средств построения ЦМР, которые не используют процедуру триангуляции и которые приводят к построению всюду гладкой поверхности.

Задачей заявляемого технического решения является расширение функциональных возможностей при картографическом отображении с одновременным повышением достоверности отображения картографической информации.

Поставленная задача решается за счет того, что в способе картографического отображения двухмерных распределений, заданных в цифровой форме, включающим преобразование изображений дискретных графических распределений в непрерывную полутоновую форму с дальнейшим их представлением в форме изолиний - эксинденсит, в котором при оптическом моделировании кодируют цифровые значения признака в заданной точке планшета оптическими символами - разновеликими пятнами с оптической плотностью, пропорциональной величине признака, построение рельефа местности, в котором построение рельефа местности выполняют путем интерполяции точек высот (глубин) в виде двумерных нерегулярных рациональных фундаментальных сплайнов, путем построения двумерной сплайн-функции, определяемой как тензорное произведение одномерных сплайнов.

Сущность способа поясняется чертежами (фиг.1, 2, 3).

Фиг.1а. Участок топографической карты. График значений высот вдоль русла реки по ЦМР, построенной с использованием триангуляции [5], где позицией 1 обозначено русло реки.

Фиг.1б. График значений высот вдоль русла реки по ЦМР, построенной с использованием триангуляции (Ястребов А.И., Демиденко А.Г. Повышение качества моделей рельефа местности, создаваемых по цифровым топографическим картам // Геопрофи. №3, 2005. - С.15-18 [5]).

Фиг.2. Основное окно программного модуля «Редактора цифровой модели рельефа v.0».

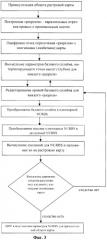
Фиг.3. Общая блок-схема реализации способа.

Заявляемый способ включает интерполяцию точек высот (глубин) методами двумерных сплайн-функций, а конкретно в виде двумерных нерегулярных рациональных фундаментальных сплайнов (NURBS) (Голованов Н.Н. Геометрическое моделирование. - М.: Физматлит, 2002. - 472 с. [6]), математические выражения которых не приводятся по причине отсутствия достаточного места. Преимуществом предлагаемого способа является выполнение интерполяции точек высот в виде двумерных рациональных двумерных сплайн-функций NURBS, что позволяют построить гладкую поверхность для любой формы рельефа, даже для обрывов с отрицательным углом наклона. Во-вторых, поверхность рельефа задается аналитической зависимостью, т.е. конечным набором параметров фиксированного набора функций (полиномиальных сплайнов). Аналитическая форма задания рельефа, т.е. в виде суперпозиции аналитических функций от двух переменных, позволяет использовать весь аппарат дифференциальной геометрии для описания морфометрических свойств рельефа, например вычисления значения функции (высоту, глубину) или ее дифференциала (уклон) в любой точке (точках) области задания функции. В-третьих, NURBS обеспечивают возможность локального редактирования формы поверхности. Кроме того, для одной и той же области земли объем массива данных ЦМР при использовании NUBRS будет как минимум на порядок меньше, чем при традиционном точечном представлении. Следовательно, применение NURBS повышает эффективность автоматизированных геопространственных систем за счет уменьшения времени обработки и требуемого объема памяти. Применение NURBS в вычислительной технике уже давно свершившийся факт - в графических пакетах всех операционных систем встроены алгоритмы обработки и визуализации NURBS, например в графических пакетах низкого уровня: DirectX и OpenGL для Windows. Однако при построении ЦМР возникают препятствия, связанные с эффектом возникновения в некоторых ситуациях нарушения монотонности в изменении поверхности - локальное появление ложных осцилляций. В заявляемом способе это препятствие устраняется либо путем добавления новых точек в массив для интерполяции, либо путем использования методов изогеометрической аппроксимации сплайнами (Квасов Б.И. Методы изогеометрической аппроксимации сплайнами. - М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2006. - 416 с. [7]). В первом случае разрешение проблемы связано с повышением значимости работы эксперта в итерационной процедуре построения NURBS, во втором с существенным усложнением математических алгоритмов технологии.

В предлагаемом способе реализована технология построения ЦМР на основе NURBS в виде итерационной экспертной автоматизированной процедуры. В качестве языка программирования использован язык MatLab. Основное окно программного модуля представлено на фиг.2. В этой системе качество построения ЦМР определяется путем экспертного сравнения положения изолиний, вычисленных по NURBS, с положением соответствующих изогипс (изобат) на исходной карте.

В конкретной реализации предлагаемого способа источником информации о рельефе служат растровые карты.

В общем случае при аппроксимации профиля рельефа одномерными сплайнами следует задавать значения двух первых производных в конечных точках разреза. Однако такая информация неизвестна, и получить ее на практике нельзя. Поэтому в качестве базового сплайна для аппроксимации профиля рельефа по разрезу использован простейший кубический сплайн с нулевыми граничными производными. Ввиду того, что не существует никаких явно заданных двумерных сплайнов, так как нельзя построить бесконечную систему алгебраических уравнений для согласования двух первых производных по всем направлениям на смежных границах двух кусков сплайновой поверхности, то построение двумерной сплайн-функции производится с использованием тензорного произведения одномерных сплайнов (Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. - Л.-М.: Наука, 1980. - 350 с. [8]). Согласование первых двух дифференциалов ЦРМ для смежных прямоугольных участков карты обеспечивается перекрытием областей задания смежных NURBS.

Таким образом, технология построения ЦМР в аналитическом виде на основе NURBS позволяет исключить этап триангуляции и тем самым исключить недостатки существующих технологий. Предлагаемая реализация технологии может быть адаптирована к другим типам исходной информации, и в нее могут быть включены более сложные типы базовых сплайнов.

Источники информации

1. Авторское свидетельство SU №365562, 1970.

2. Авторское свидетельство SU №640113, 1978.

3. Берлянт A.M. Картография. - М.: Аспект Пресс, 2002. - 336 с.

4. Суворов С.Г., Дворецкий Е.М., Коваленко С.А. Методика создания цифровых моделей рельефа повышенной точности // Информация и космос. №1, 2005. - С.52-54.

5. Ястребов А.И., Демиденко А.Г. Повышение качества моделей рельефа местности, создаваемых по цифровым топографическим картам // Геопрофи. №3, 2005. - С.15-18.

6. Голованов Н.Н. Геометрическое моделирование. - М.: Физматлит, 2002. - 472 с.

7. Квасов Б.И. Методы изогеометрической аппроксимации сплайнами. - М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2006. - 416 с.

8. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функций. - Л.-М.: Наука, 1980. - 350 с.

Способ картографического отображения двухмерных распределений, заданных в цифровой форме, включающий преобразование изображений дискретных графических распределений в непрерывную полутоновую форму с дальнейшим их представлением в форме изолиний - эксинденсит, в котором при оптическом моделировании кодируют цифровые значения признака в заданной точке планшета оптическими символами -разновеликими пятнами с оптической плотностью, пропорциональной величине признака, построение рельефа местности, отличающийся тем, что построение рельефа местности выполняют путем интерполяции точек высот и/или глубин в виде двумерных нерегулярных рациональных фундаментальных сплайнов, путем построения двумерной сплайн-функции, определяемой как тензорное произведение одномерных сплайнов.