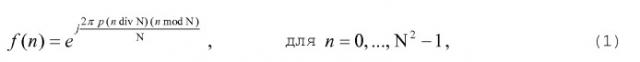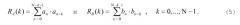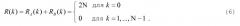Способ и устройство для обработки первичных и вторичных сигналов синхронизации для беспроводной связи

Способ и устройство для обработки первичных и вторичных сигналов синхронизации для беспроводной связи

Иллюстрации

Показать все

Реферат

Настоящая заявка испрашивает приоритет предварительной патентной заявки США № 60/828,055, озаглавленной «Способ и устройство для P-SCH и S-SCH последовательностей для Е-UTRA», поданной 3 октября 2007, переуступленной правопреемнику настоящей заявки и включенной в настоящий документ посредством ссылки.

Область техники

Настоящее раскрытие относится в общем к связи, более конкретно к способам синхронизации для беспроводной связи.

Уровень техники

Системы беспроводной связи широко используются для предоставления различного коммуникационного контента, такого как голос, видео, пакетные данные, передача сообщений, широковещание и т.д. Эти беспроводные системы могут быть системами множественного доступа, способными поддерживать множество пользователей путем совместного использования доступных ресурсов системы. Примеры таких систем множественного доступа включают в себя системы множественного доступа с кодовым разделением (CDMA), системы множественного доступа с временным разделением (TDMA), системы множественного доступа с частотным разделением (FDMA), системы ортогонального FDMA (OFDMA) и системы FDMA с одной несущей (SC-FDMA).

Система беспроводной связи может включать в себя любое число базовых станций, которые могут поддерживать коммуникацию для любого количества единиц пользовательского оборудования (UE). UE (например, сотовый телефон) может находиться в пределах зоны покрытия связью ни одной, одной или множества базовых станций в любой данный момент. UE могло быть только что включено или могло потерять покрытие связью и, таким образом, может не знать, какие базовые станции могут приниматься. UE может выполнить поиск ячейки, чтобы обнаружить базовые станции и получить информацию временных характеристик (хронирования) и другую информацию для обнаруженных базовых станций.

Каждая базовая станция может передать сигналы синхронизации, чтобы помочь UE выполнять поиск ячейки. Вообще, сигнал синхронизации может быть любым сигналом, который позволяет приемнику обнаруживать передатчик и получать временные характеристики и/или другую информацию. Сигналы синхронизации представляют непроизводительные затраты и должны передаваться с максимально возможной эффективностью. Кроме того, сигналы синхронизации должны позволить UE выполнять поиск ячейки максимально быстро и эффективно.

Сущность изобретения

Описаны способы обеспечения поиска ячейки посредством UE в системе беспроводной связи. В одном аспекте последовательность первичного кода синхронизации (PSC) может генерироваться на основе последовательности Frank и последовательности постоянной амплитуды, которая повторяется многократно. Последовательность Frank может обеспечить хороший показатель по сдвигу частоты и оценке канала. Последовательность постоянной амплитуды может обеспечить хороший показатель по частичной корреляции. Последовательность постоянной амплитуды может быть основана на последовательности Golay, М-последовательности, псевдослучайной (PN) последовательности и т.д. В одном варианте повторяемая последовательность постоянной амплитуды длины N² может быть получена путем повторения N раз последовательности постоянной амплитуды длины N. Последовательность PSC длины N² может генерироваться на основе последовательности Frank длины N² и повторяемой последовательности постоянной амплитуды длины N².

В другом аспекте набор последовательностей PSC может генерироваться на основе комплементарных последовательностей, имеющих хорошие апериодические свойства корреляции и эффективные реализации. В одном варианте последовательности PSC A+B и B+A могут быть сформированы на основе комплементарных последовательностей Golay A и B, где "+" обозначает конкатенацию. Обнаружение последовательностей PSC A+B и B+A может быть эффективно выполнено с намного меньшим количеством арифметических операций, чем для других типов последовательностей PSC.

В еще одном аспекте набор последовательностей вторичного кода синхронизации (SSC) может генерироваться на основе набора базовых последовательностей и различных символов модуляции для схемы модуляции. Базовые последовательности могут быть последовательностями CAZAC (постоянной амплитуды с нулевой автокорреляцией), PN-последовательностями, комплементарными последовательностями и т.д. Каждая базовая последовательность может модулироваться каждым из М возможных символов модуляции для схемы модуляции, чтобы получить М различных последовательностей SSC. UE может получить оценку канала, основанную на обнаруженном PSC, и может выполнить когерентное обнаружение с оценкой канала, чтобы определить символ модуляции, посланный в базовой последовательности.

Различные аспекты и признаки раскрытия описаны ниже детально.

Краткое описание чертежей

Фиг.1 - система беспроводной связи.

Фиг.2 - приведенная в качестве примера передача PSC и SSC.

Фиг.3 - коррелятор комплементарной последовательности Golay.

Фиг.4 - блок-схема узла B и UE.

Фиг.5 - блок-схема процессора данных передачи (ТХ) в узле В.

Фиг.6A и 6B - блок-схемы двух генераторов сигнала PSC.

Фиг.6C - блок-схема генератора сигнала SSC.

Фиг.7 - блок-схема процессора синхронизации в UE.

Фиг.8-19 - процессы и устройства для генерации сигналов PSC и SSC узлом B и для обнаружения сигналов PSC и SSC посредством UE.

Детальное описание

Методы, описанные здесь, могут использоваться для различных систем беспроводной связи, таких как CDMA, TDMA, FDMA, OFDMA, SC-FDMA и другие системы. Термины "система" и "сеть" часто используются взаимозаменяемым образом. Система CDMA может реализовывать такую технологию радиосвязи, как Универсальный наземный радиодоступ (UTRA), cdma2000 и т.д. UTRA включает в себя широкополосный CDMA (W-CDMA) и LCR (Низкая скорость элементарных посылок). Технология cdma2000 включает в себя стандарты IS-2000, IS-95 и IS-856. Система TDMA может реализовывать такую технологию радиосвязи, как Глобальная система мобильной связи (GSM). Система OFDMA может реализовывать такую технологию радиосвязи, как Е-UTRA (Развитый UTRA), UMB (Ультраширокополосная мобильная технология), IEEE 802.11 (Wi-Fi), IEEE 802.16 (WiMAX), IEEE 802.20, Flash-OFDM®, и т.д. UTRA, E-UTRA и GSM являются частью Универсальной Мобильной Телекоммуникационной Системы (UMTS). 3GPP LTE (Долгосрочное развитие стандарта 3GPP) является планируемым выпуском UMTS, который использует Е-UTRA, применяющий OFDMA в нисходящей линии и SC-FDMA в восходящей линии. UTRA, Е-UTRA, GSM, UMTS и LTE описаны в документах организации 3GPP ("Проект партнерства третьего поколения"). cdma2000 и UMB описаны в документах организации 3GPP2 ("Проект 2 партнерства третьего поколения"). Эти различные технологии радиосвязи и стандарты известны в технике.

Фиг.1 показывает систему беспроводной связи 100 с множеством узлов В 110. Узел B может быть неподвижной станцией, используемой для связи с UE, и может также упоминаться как усовершенствованный узел B (eNB), базовая станция, пункт доступа и т.д. Каждый узел B 110 обеспечивает покрытие связью для конкретной географической области. Полная зона покрытия каждого узла B 100 может быть разделена на множество (например, три) меньших областей. В 3GPP термин "ячейка" может относиться к наименьшей зоне покрытия узла B и/или подсистемы узла B, обслуживающей эту зону покрытия. В других системах термин "сектор" может относиться к наименьшей зоне покрытия и/или подсистеме, обслуживающей эту зону покрытия. Для ясности в нижеследующем описании используется 3GPP концепция ячеек.

UE 120 могут быть рассредоточены по системе. UE может быть стационарным или мобильным и может также упоминаться как мобильная станция, терминал, терминал доступа, абонентский блок, станция и т.д. UE может быть сотовым телефоном, персональным цифровым помощником (PDA), беспроводным модемом, устройством беспроводной связи, переносным устройством, ноутбуком, беспроводным телефоном и т.д. UE может осуществлять связь с одним или более узлами В посредством передач по нисходящей линии и восходящей линии. Передача информации по нисходящей линии (или по прямой линии связи) относится к линии связи от узлов к UE, а восходящая линия (или обратная линия связи) относится к линии связи от UE к узлам В. На фиг.1 сплошная линия с двойными стрелками указывает на связь между узлом B и UE. Прерывистая линия с единственной стрелкой указывает UE, принимающее сигнал нисходящей линии от узла B. UE может выполнить поиск ячейки, основываясь на сигналах нисходящей линии, переданных узлами В.

В системе 100 узлы В 110 могут периодически передавать сигналы синхронизации, чтобы позволить UE 120 обнаруживать узлы В и получать информацию, такую как временные характеристики (хронирование), сдвиг частоты, идентификатор (ИД) ячейки и т.д. Сигналы синхронизации могут генерироваться и передаваться по-разному. В одном варианте, который описан подробно ниже, каждый узел B периодически передает сигнал PSC и сигнал SSC. Сигнал PSC может генерироваться на основе последовательности PSC и посылаться на первичном канале синхронизации (P-SCH). Сигнал SSC может генерироваться на основе последовательности SSC и посылаться на вторичном канале синхронизации (S-SCH). PSC и SSC могут также упоминаться под другими названиями, такими как первичная и вторичная последовательности синхронизации.

На фиг.2 показана приведенная в качестве примера передача PSC и SSC в соответствии с одной схемой. График времени передачи для нисходящей линии может быть разделен на блоки радиокадров. Каждый радиокадр может иметь предопределенную продолжительность, например 10 миллисекунд (мс). В схеме, показанной на фиг.2, PSC посылается вблизи начала и середины радиокадра, а SSC посылается непосредственно перед PSC. Вообще, PSC может посылаться с любой частотой, например любое количество раз в каждом радиокадре. SSC может также посылаться с любой частотой, которая может быть той же самой или отличающейся от частоты посылки PSC. SSC может посылаться рядом с PSC (например, или непосредственно перед, или после PSC) так, чтобы оценка канала, полученная из PSC, могла использоваться для когерентного обнаружения SSC, как описано ниже.

В одной схеме все ячейки могут передавать ту же самую последовательность PSC, чтобы позволить UE обнаруживать эти ячейки. Различные ячейки могут передавать различные последовательности SSC, чтобы позволить UE идентифицировать эти ячейки и, возможно, получать дополнительную информацию из ячеек. Число последовательностей SSC может зависеть от числа поддерживаемых идентификаторов (ИД) ячеек и/или другой информации, посылаемой в SSC.

UE может выполнять поиск ячейки (например, при включении питания) с использованием двухэтапного процесса обнаружения. В одной схеме двухэтапный процесс обнаружения может включать:

1. Стадию обнаружения PSC -

a. Обнаружить ячейки, основываясь на PSC, переданном ячейками,

b. Получить временные характеристики символа и, возможно, временные характеристики для каждой обнаруженной ячейки, и

c. Оценить сдвиг частоты и отклик канала для каждой обнаруженной ячейки; и

2. Стадию обнаружения SSC -

a. Идентифицировать каждую обнаруженную ячейку, основываясь на SSC, переданном ячейкой, и

b. Получить временные характеристики кадра, если не обеспечено стадией обнаружения PSC.

UE может также получить другую информацию (например, информацию циклического префикса, информацию передающей антенны и т.д.), основываясь на PSC и SSC.

Поиск ячейки может быть относительно сложным и может потреблять значительную мощность питания от батареи для переносного устройства. Для стадии обнаружения PSC временные характеристики символа/кадра могут быть неизвестными, так что UE может коррелировать принятый сигнал с локально генерированной последовательностью PSC при различных гипотезах временных характеристик (или смещений времени), чтобы обнаружить последовательность PSC, переданную ячейкой. Для стадии обнаружения SSC временные характеристики символа/кадра могут быть известными из стадии обнаружения PSC, но может иметься множество гипотез SSC (например, ИД ячейки) для проверки. UE может коррелировать принятый сигнал с различными последовательностями-кандидатами SSC, чтобы обнаружить последовательность SSC, переданную ячейкой. Последовательности PSC и SSC могут быть разработаны, чтобы уменьшить сложность обнаружения PSC и SSC посредством UE.

Низкая сложность и высокая эффективность обнаружения желательны как для PSC, так и для SSC. Для повышения эффективности обнаружения SSC, UE может выполнять когерентное обнаружение SSC для каждой обнаруживаемой ячейки, основываясь на оценке канала, полученной из PSC для той ячейки. PSC может, таким образом, разрабатываться так, чтобы иметь хорошие свойства автокорреляции, обеспечивать хорошие характеристики по сдвигу частоты и оценке канала и иметь низкую сложность обнаружения.

Последовательность CAZAC может использоваться для PSC. Некоторые примерные последовательности CAZAC включают в себя последовательность Frank, последовательность Chu, обобщенную ЛЧМ-подобную последовательность (GCL) и т.д. Последовательность CAZAC может обеспечить нулевую автокорреляцию, которая имеет большое значение для корреляции последовательности CAZAC с самой собой при нулевом сдвиге и нулевые значения для всех сдвигов. Свойство нулевой автокорреляции выгодно для того, чтобы точно оценить отклик канала и уменьшить время поиска временных характеристик. Однако последовательности GCL и Chu имеют неоднозначность между сдвигом времени и сдвигом частоты, что означает, что ошибка хронирования в приемнике вызывает соответствующее линейное изменение фазы во временной области или эквивалентный сдвиг частоты в частотной области. Таким образом, эффективность оценки сдвига частоты может быть ухудшена, так как не было бы известно, обусловлен ли обнаруженный сдвиг частоты в приемнике ошибкой частоты или ошибкой хронирования в приемнике. Последовательность Frank ухудшила эффективность частичной корреляции. Частичная корреляция относится к корреляции принятого сигнала с частью последовательности вместо всей последовательности. Частичная корреляция может обеспечить повышенную эффективность обнаружения по полной корреляции (которая является корреляцией по всей последовательности), когда большой сдвиг частоты присутствует в приемнике. Частичная корреляция может быть выполнена по подходящей продолжительности времени, которая может быть определена на основе максимального ожидаемого сдвига частоты в приемнике. Однако пик автокорреляции для последовательности Frank может быть широким для частичной корреляции. Для хороших показателей работы PSC должен обеспечить хорошую способность оценки канала без потенциальной проблемы в оценке сдвига частоты и в отсутствие проблем с частичной корреляцией.

В одном аспекте последовательность PSC может генерироваться на основе последовательности Frank и последовательности постоянной амплитуды, которая повторяется многократно. Последовательность Frank может обеспечить высокую эффективность по сдвигу частоты и оценке канала. Последовательность постоянной амплитуды может обеспечить высокую эффективность по частичной корреляции.

Последовательность Frank f(n) может быть выражена как:

где N и p могут быть любыми положительными целочисленными значениями, относительно простыми друг к другу, и N² - длина последовательности Frank.

В уравнении (1) p - индекс последовательности для последовательности Frank. Различные последовательности Frank могут генерироваться с различными значениями р.

Последовательность постоянной амплитуды может быть любой последовательностью, имеющей постоянную амплитуду и хорошие свойства автокорреляции. Например, последовательность постоянной амплитуды может быть основана на последовательности Golay, комплементарной последовательности Golay, М-последовательности максимальной длины, PN-последовательности и т.д. Последовательности Golay и комплементарные последовательности Golay различных длин могут генерироваться способом, известным в технике. М-последовательность является PN-последовательностью максимальной длины 2^L - 1 и генерируется на основе примитивного полинома, где L может быть любым целочисленным значением. Последовательность постоянной амплитуды длины 2^L может быть получена из М-последовательности длины 2^L - 1, добавляя или +1 или -1 к М-последовательности так, чтобы количество «+1» было равно количеству «-1». Вообще, длина последовательности постоянной амплитуды может быть любым целочисленным делителем N², так чтобы длина последовательности Frank была целым кратным длины последовательности постоянной амплитуды.

В одной схеме последовательность постоянной амплитуды длины N повторена N раз, чтобы получить повторяющуюся последовательность постоянной амплитуды длины N², следующим образом:

где c_i(n) является i-й копией последовательности постоянной амплитуды, для i = 0,…, N-1,

при с₀(n) = c₁(n) =… = c_i(n) =… = c_N-1(n), и

c(n) - повторяющаяся последовательность постоянной амплитуды длины N².

Последовательность PSC может тогда генерироваться следующим образом:

p(n) = f(n)·c(n), для n=0,…, N²-1, (3)

где p(n) является последовательностью PSC длины N².

В одной иллюстративной схеме последовательность PSC длины 64 может генерироваться умножением последовательности Frank длины 64 на повторяющуюся последовательность постоянной амплитуды длины 64. Повторяющаяся последовательность постоянной амплитуды может быть получена повторением комплементарной последовательности Golay длины 8 {1, 1, 1, -1, 1, 1, -1, 1} восемь раз.

Произведение последовательности Frank длины N² и повторяющейся последовательности постоянной амплитуды (например, генерированной N повторениями последовательности постоянной амплитуды длины N с хорошим свойством автокорреляции) может улучшить частичную корреляцию и эффективность объединения энергии. Повторяющаяся последовательность постоянной амплитуды может подавить помехи многолучевого распространения, что может способствовать повышению эффективности частичной корреляции. После коррекции сдвига временных характеристик и частоты точная оценка канала (из-за свойства CAZAC последовательности Frank) может быть получена путем удаления последовательности PSC, как описано ниже.

В другом аспекте ряд последовательностей PSC может генерироваться на основе комплементарных последовательностей, имеющих хорошие апериодические свойства корреляции и эффективные реализации. Пара комплементарных последовательностей A и B может быть выражена как:

A=[a₀ a₁ … a_N-1] и (4)

В=[b₀ b₁ … b_N-1],

где a_n и b_n являются n-м элементом комплементарных последовательностей A и B соответственно.

Апериодическая функция автокорреляции R_A(k) для последовательности A и апериодическая функция автокорреляции R_B(k) для последовательности B могут быть выражены как:

Для комплементарных последовательностей A и B сумма их апериодических функций корреляции равна нулю для всех положений, кроме положения при нулевой задержке, следующим образом:

Последовательности PSC могут генерироваться на основе различных типов комплементарных последовательностей, таких как комплементарные последовательности Golay (GCS), иерархические комплементарные последовательности Golay и т.д. Комплементарные последовательности Golay имеют хорошие апериодические свойства корреляции, как показано в уравнениях (5) и (6). Кроме того, для бинарных комплементарных последовательностей Golay длины N, коррелятор GCS может быть эффективно реализован с использованием только 2log₂(N) комплексных сложений, как описано ниже.

Комплементарные последовательности Golay различных длин могут генерироваться по-разному. Прямой способ конструирования для генерации различных пар комплементарных последовательностей Golay любой длины N описан Marcel J.E. Golay в статье "Complementary Series", IRE Trans. Inform. Theory, IT-7:82-87, 1961. N различных пар комплементарных последовательностей Golay длины N могут также быть получены умножением пары комплементарных последовательностей Golay длины N на N×N матрицу Адамара.

Последовательности PSC могут генерироваться на основе комплементарных последовательностей A и B различными способами. В одной схеме пара последовательностей PSC PSC₁ и PSC₂ длины 2N может генерироваться следующим образом:

PSC₁ = A + B, и (7)

PSC₂ = B + A.

В схеме, показанной в уравнении (7), PSC₁ генерируется конкатенацией комплементарной последовательности А с комплементарной последовательностью B, и PSC₂ генерируется конкатенацией комплементарной последовательности В с комплементарной последовательностью А. Например, последовательности PSC длины 64 могут генерироваться конкатенацией комплементарных последовательностей A и B длины 32.

В другой схеме пара последовательностей PSC длины N может генерироваться следующим образом:

PSC₁ = A, и (8)

PSC₂ = B.

В схеме, показанной в уравнении (8), последовательности PSC длины 64 могут генерироваться на основе комплементарных последовательностей A и B длины 64. Использование более длинных комплементарных последовательностей A и B для PSC может уменьшить сложность обнаружения. Более длинные комплементарные последовательности длиной 64 могут также иметь более низкий уровень бокового лепестка, чем у комплементарных последовательностей длиной 32, используемых для схемы согласно уравнению (7).

Другие последовательности PSC могут также генерироваться, например PSC₁=А+A и PSC₂=B+B. В любом случае для последовательностей PSC, генерированных на основе комплементарных последовательностей Golay A и B, коррелятор GCS может быть эффективно реализован с использованием свойств комплементарных последовательностей Golay.

Фиг.3 показывает схему коррелятора GCS 300, который может использоваться, чтобы выполнить скользящую корреляцию для комплементарных последовательностей Golay A и B. Коррелятор GCS 300 включает в себя S секций, где S = log₂(N) и N является длиной комплементарных последовательностей Golay. Например, S=5 секций могут использоваться для корреляции комплементарных последовательностей Golay длины N = 32.

Первая секция принимает входные выборки r(n). Каждая последующая секция s, для s=2,…, S, принимает результаты частичной корреляции a_s-1(n) и b_s-1(n) от предшествующей секции и предоставляет результаты частичной корреляции a_s(n) и b_s(n) на следующую секцию. Последняя секция S предоставляет результаты корреляции А(n) и B(n) для комплементарных последовательностей Golay A и B соответственно.

Каждая секция включает в себя блок задержки 322, умножитель 324 и сумматоры 326 и 328. Для секции s блок задержки 322 принимает a_s-1(n) от предшествующей секции s-l и обеспечивает задержку D_s выборок. Умножитель 324 принимает b_s-1(n) от предшествующей секции s-l и умножает b_s-1(n) на вес W*_s. Сумматор 326 суммирует выходы блока задержки 322 и умножителя 324 и предоставляет a_s(n) в следующую секцию. Сумматор 328 вычитает выход умножителя 324 из выхода блока задержки 322 и предоставляет b_s(n) в следующую секцию.

После начальной задержки N-1 элементарных посылок последняя секция S предоставляет одну пару результатов корреляции А(n) и B(n) для каждой входной выборки r(n). Сумматор 326 в последней секции S обеспечивает результат корреляции А(n) для корреляции N самых последних входных выборок с комплементарной последовательностью Golay A. Сумматор 328 в последней секции S обеспечивает результат корреляции B(n) для корреляции N самых последних входных выборок с комплементарной последовательностью Golay B.

Задержки от D₁ до D_S и веса от W₁ до W_S для S секций могут быть определены на основе определенных комплементарных последовательностей Golay A и B, выбранных для использования. В одной схеме задержки от D₁ до D_S для S секций могут быть такими, что D₁=N/2 для первой секции и D_s=D_s-1/2 для каждой последующей секции. Веса от W₁ до W_S для S секций могут быть такими, что W_s ∈ {+1,-1} для бинарных комплементарных последовательностей Golay. Различные задержки от D₁ до D_S и веса от W₁ до W_S могут использоваться для различных пар комплементарных последовательностей Golay A и B.

Выходная секция включает в себя блоки задержки 332 и 334 и сумматоры 336 и 338. Блоки задержки 332 и 334 задерживают результаты корреляции А(n) и B(n) соответственно на N периодов выборок. Сумматор 336 суммирует результат корреляции А(n) с сумматора 326 с задержанным результатом корреляции В(n-N) c блока задержки 334 и обеспечивает заключительный результат корреляции для PSC₁=А+B. Сумматор 338 суммирует результат корреляции В(n) с сумматора 328 с задержанным результатом корреляции А(n-N) c блока задержки 332 и обеспечивает заключительный результат корреляции для PSC₂ =В+А.

Для схемы, соответствующей уравнению (7), коррелятор GCS 300 может выполнить корреляцию для каждой половины PSC, чтобы получить результаты частичной корреляции А(n) и B(n) для этой половины PSC. Поскольку веса от W₁ до W_S равны +1 или -1, сложность корреляции определяется числом комплексных сложений/вычитаний. Для каждой половины PSC с N = 32, коррелятор GCS 300 может выполнить корреляцию для обеих комплементарных последовательностей A и для B с только 2log₂(32)=10 комплексными сложениями. Два результата частичной корреляции А(n) и B(n) могут быть получены для второй половины PSC для данной гипотезы n хронирования. Два результата частичной корреляции А(n-N) и B(n-N) могут быть получены для первой половины PSC для той же самой гипотезы хронирования в предшествующий период n-N выборки и сохранены в блоках задержки 332 и 334. Еще одно суммирование может тогда быть выполнено сумматором 336, чтобы объединить два результата частичной корреляции А(n) и B(n-N), чтобы получить заключительный результат корреляции для PSC₁=А+B. Еще одно суммирование может быть выполнено сумматором 338, чтобы объединить два результата корреляции B(n) и А(n-N), чтобы получить заключительный результат корреляции для PSC₂=В+А.

Для схемы, показанной в уравнении (7), частичная корреляция может быть выполнена для каждой половины PSC, чтобы противодействовать большому сдвигу частоты в приемнике. Сложность для получения грубого хронирования может быть уменьшена с использованием результатов частичной корреляции. Для каждой гипотезы хронирования результаты частичной корреляции определяются для последовательностей A+0 и 0+B и могут использоваться, чтобы исключить многих кандидатов. Например, если результаты частичной корреляции ниже порога, то полная корреляция для последовательностей A+B и A+B может быть пропущена. Те же самые методы обнаружения могут также использоваться для схемы A+A и B+B.

Результаты частичной корреляции для каждой половины PSC являются комплексными значениями и могут использоваться, чтобы оценить сдвиг частоты. Сдвиг фазы θ(n) может быть оценен на основе результатов частичной корреляции следующим образом:

где "*" обозначает комплексное сопряжение. Уравнение (9a) может использоваться, если обнаруживается A+B, а уравнение (9b) может использоваться, если обнаруживается B+A.

Оценка сдвига частоты может быть получена на основе оценки сдвига фазы следующим образом:

где T_GCS - длительность комплементарных последовательностей Golay в секундах.

Сложность обнаружения последовательностей PSC A+B и B+A, по существу, та же самая. Один информационный бит может быть передан путем передачи A+B или B+A. Например, A+B может быть передано для передачи битового значения '1', и B+A может быть передано для передачи битового значения '0'. Информационный бит может указать одну из двух возможных длин циклического префикса или может передать другую информацию. С еще двумя суммированиями могут быть проверены обе гипотезы A+B и B+A, и информационный бит может быть восстановлен из успешной гипотезы. Если PSC передается многократно в радиокадре, то может передаваться более одного информационного бита путем передачи различных комбинаций последовательностей PSC в одном радиокадре.

Для схемы последовательностей PSC A и B, соответствующей уравнению (8), один информационный бит может быть передан путем передачи A или B. Например, PSC может передаваться дважды в одном радиокадре, А с последующим B может передаваться для передачи битового значения '1', и B с последующим A может передаваться для передачи битового значения '0'. Один информационный бит может также быть включен для схемы с PSC=C+A при PSC, передаваемом один или два раза в одном кадре.

Можно показать, что N·log₂(N)! различных пар комплементарных последовательностей Golay длины N могут генерироваться для данного N. Если одна пара комплементарных последовательностей Golay используется для всех ячеек, то эта пара GCS может быть выбрана так, чтобы иметь (i) низкий уровень бокового лепестка в апериодических автокорреляциях, или низкие R_A(k) и R_B(k) для k=1,…, N-1, (ii) низкую взаимную корреляцию между двумя комплементарными последовательностями Golay и (iii) низкие вариации в частотной характеристике, чтобы обеспечить хороший показатель оценки канала.

Множество пар комплементарных последовательностей Golay могут также использоваться для генерации большего количества последовательностей PSC. Например, две пары комплементарных последовательностей Golay (A₁, В₁) и (A₂, B₂) могут использоваться для генерации четырех последовательностей PSC, от PSC₁ до PSC₄, следующим образом:

С четырьмя последовательностями PSC ячейки в системе могут быть разделены на четыре группы 1-4, причем каждая ячейка принадлежит только одной группе. Группы 1-4 могут быть связаны с PSC₁-PSC₄ соответственно. Ячейки в каждой группе могут использовать последовательность PSC для той группы. Сложность обнаружения может быть уменьшена путем повторного использования результатов частичной корреляции, чтобы получить заключительные результаты корреляции для различных PSC. Например, результат частичной корреляции A₁(n) для комплементарной последовательности Golay А₁ для более поздней половины PSC₁ может быть повторно использован как результат частичной корреляции A₁(n-N) для комплементарной последовательности Golay А₁ для более ранней половины PSC₃.

Вообще, ячейки могут быть разделены в любое число групп, и достаточное число последовательностей PSC может генерироваться для этих групп. Разделение ячеек во множество групп может позволить UE получать более точную оценку канала, так как оценка канала, полученная для данной последовательности PSC, будет испытывать помехи только от ячеек, использующих эту PSC (вместо всех ячеек, если только одна PSC будет использоваться всеми ячейками).

Последовательности PSC, генерируемые на основе комплементарных последовательностей Golay, могут иметь намного более низкую сложность обнаружения, чем последовательности PSC, генерированные на основе PN-последовательностей или комплексных последовательностей. Для каждой гипотезы хронирования полная корреляция для последовательности PSC длиной 64 может быть выполнена с (i) 12 комплексными сложениями для комплементарных последовательностей Golay, (ii) 63 комплексными сложениями для PN-последовательности или (iii) 64 комплексными умножениями и 63 комплексными сложениями для комплексной последовательности.

Для всех последовательностей PSC, описанных выше, множество последовательностей PSC могут передаваться в одном радиокадре и могут неравномерно размещаться в радиокадре. Например, одна последовательность PSC может быть передана в начале или вблизи начала радиокадра длительностью 10 миллисекунд, а другая последовательность PSC может быть передана приблизительно спустя 4,5 миллисекунды от начала радиокадра. В этом случае UE может выполнять параллельный поиск шаблона и может выполнять поиск по всем возможным комбинациям неравномерно разнесенных шаблонов и выбирать лучшего кандидата на каждую гипотезу.

SSC может использоваться для передачи ИД ячейки и/или другой информации. Большой набор последовательностей SSC может быть определен, и соседним ячейкам могут назначаться различные последовательности SSC, которые могут использоваться, чтобы отличить эти ячейки. Например, большой набор ортогональных или псевдоортогональных последовательностей может использоваться для последовательностей SSC. Эти ортогональные или псевдоортогональные последовательности могут генерироваться на основе последовательности Chu или GCL с различными индексами последовательности, PN-последовательностей частотной области и т.д. Различные сдвиги времени могут также использоваться, чтобы генерировать множество псевдоортогональных последовательностей. Набор ортогональных или псевдоортогональных последовательностей должен быть выбран на основе корреляционных свойств и сложности. В любом случае, независимо от конкретного типа ортогональных или псевдоортогональных последовательностей, выбранных для использования, сложность обнаружения может быть высокой для большого размера набора, так как сложность пропорциональна числу последовательностей в наборе. Сложность обнаружения может быть уменьшена при использовании малого размера набора, но это может не обеспечить достаточное число ИД ячеек.

В еще одном аспекте модулированные по фазе последовательности могут использоваться, чтобы получить больший размер набора и/или уменьшить сложность обнаружения для SSC. Набор базовых последовательностей может генерироваться на основе последовательности CAZAC с различными индексами последовательности, различных PN-последовательностей, различных комплементарных последовательностей и т.д. Последовательность CAZAC может быть последовательностью Chu, последовательностью Frank, последовательностью GCL и т.д. Каждая базовая последовательность может модулироваться различными возможными символами модуляции из выбранной схемы модуляции, чтобы получить различные возможные последовательности SSC. Если используется двоичная фазовая манипуляция (BPSK), то каждая базовая последовательность может модулироваться двумя возможными символами BPSK (например, +1 и -1), чтобы получить две последовательности SSC. Если используется квадратурная фазовая манипуляция (QPSK), то каждая базовая последовательность может модулироваться четырьмя возможными символами QPSK (например, 1+j, -1+j, 1-j и -1-j), чтобы получить четыре последовательности SSC. Число последовательностей SSC может, таким образом, быть увеличено в М раз, где М - число символов модуляции для выбранной схемы модуляции.

Для стадии обнаружения SSC, UE может сначала коррелировать принятый сигнал с различными возможными базовыми последовательностями. Сложность обнаружения может быть уменьшена в 1/М, так как число базовых последовательностей равно 1/М, умноженному на число последовательностей SSC. Альтернативно, больший набор последовательностей SSC может поддерживаться для данной сложности обнаружения. В любом случае, после обнаружения конкретной базовой последовательности из корреляции с различными возможными базовыми последовательностями, когерентное обнаружение может быть выполнено для обнаруженной базовой последовательности с оценкой канала, полученной из PSC, чтобы определить, какая из М возможных последовательностей SSC была послана. Это когерентное обнаружение или идентификация на основе модулированной фазы может быть выполнена с минимальными дополнительными операциями.

Набор из Q модулированных по фазе последовательностей SSC может иметь показатели, подобные соответствующим показателям набора из Q ортогональных или псевдоортогональных последовательностей. Однако сложность обнаружения может быть уменьшена в 1/М (например, 1/4 для QPSK или 1/2 для BPSK), или может быть разрешено в М раз больше гипотез. Более высокий порядок модуляции (например, 8-PSK, 16-QAM и т.д.) может также использоваться, чтобы дополнительно уменьшить сложность обнаружения или дополнительно увеличить число последовательностей SSC.

Фиг.4 показывает блок-схему узла B 110 и UE 120, которые являются одним из узлов В и одним из U