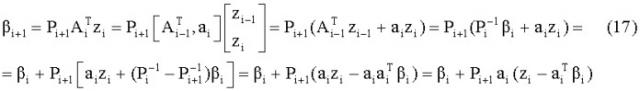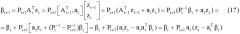Способ идентификации аэродинамических характеристик летательного аппарата по результатам испытаний

Способ идентификации аэродинамических характеристик летательного аппарата по результатам испытаний

Иллюстрации

Показать все

Реферат

Изобретение относится к области авиации, а именно к способам идентификации аэродинамических характеристик при проведении исследований летательных аппаратов. Способ включает оценивание параметров математической модели движения ЛА - аэродинамических характеристик и направлен на повышение точности идентификации.

Известен способ определения параметров математической модели по результатам испытаний, см. «Теория управления» К.Спиди, Р.Браун, Д.Гудвин. М.: Мир. 1973, стр.55.

Задача оценивания аэродинамических характеристик летательного аппарата на основе идентификации математической модели движения ЛА имеет простое решение в случае использования метода наименьших квадратов (МНК) и линейной по параметрам математической модели. В методе наименьших квадратов параметры модели определяются из условия обращения в минимум суммы квадратов невязок уравнений движения, взятых в дискретной последовательности равноотстоящих моментов времени на заданном интервале наблюдения векторов состояния и управления ЛА. Невязка обусловливается неточностью выбора структуры модели, неучтенным взаимодействием среды и системы, ошибками и помехами измерений. Независимо от физического происхождения невязок они определяются как разность между правой и левой частями математической модели, полученную при подстановке в математическое выражение модели измеренных в эксперименте значений элементов векторов состояния и управления летательного аппарата.

Пусть наблюдаемые переменные x и y связаны линейной зависимостью вида

и получены из эксперимента n пар значений x_i и y_i (r=1,…,n), тогда на основе критерия наименьших квадратов находят наилучшие значения констант a и b и оценивают их точность.

При подстановке какой-либо пары значений в уравнение (1) будет иметь место невязка, обусловленная ошибкой измерения, т.е.

В соответствии с принципом метода наименьших квадратов для определения наилучших значений a и b следует потребовать выполнения условия

где

т.е. подобрать такие значения a и b, при которых условие (3) выполняется. Для нахождения минимума функции U(a, b) берутся частные производные от U по а и b приравниваются нулю

Решают систему уравнений относительно а и b, получают

Найденные значения a и b определяют ту прямую, которая в среднем лучше всего отвечает критерию наименьших квадратов.

Рекуррентная формула - соотношение вида

позволяет вычислять члены последовательности, если заданы ее первые p членов.

В случае, когда рекуррентное соотношение линейно (возвратная последовательность) задача описания множества всех последовательностей удовлетворяющих данному рекуррентному соотношению имеет аналогию с решением обыкновенного линейного дифференциального уравнения с постоянными коэффициентами.

Однако МНК предназначен для постобработки материалов летных испытаний и не может быть использован в системах реального времени, т.е. не обладает записью соотношений в рекуррентной форме.

Известен способ обработки результатов летных испытаний (взят за прототип), см. «Теория управления» К.Спиди, Р.Браун, Д.Гудвин. М.: Мир. 1973, стр.84. Рекуррентное оценивание по методу наименьших квадратов.

Проводят некоторое количество измерений, так что система содержит i скалярных уравнений. Записывают систему в виде

Проводят измерения в i момент времени и получают

Или в блочном виде:

где индексы i и i+1, соответствующие β, показывают число уравнений в системе, которую для оценки β решают в смысле минимума среднеквадратической ошибки.

Из уравнений (9, 10) следует

где

и

Из преобразования над матрицами следует, что Р_i+1 допускает представление в виде

Уравнения (15, 16) рекуррентные, что позволяет вычисление P_i+1 при известном P_i. Тем не менее для вычисления P_i+1 используют (16), а не (15), так как множитель скалярный и поэтому допускает простейшее обращение.

Получают

Данные формулы позволяют вычисление новой оценки параметра β_i+1, если заданы предыдущая оценка β_i, оценка P_i и информация об , z_i по измерениям в момент времени t. Для оценивания по рекуррентной схеме вычисляют матрицу P₀ и β₀, воспользовавшись вышеприведенными соотношениями.

Однако данный способ предполагает накопление измерений и уточнения оценок с приходом «новой» по времени информации, а «старая» информация не удаляется из матрицы, содержащей экспериментальные данные, поэтому интервал наблюдений расширяется, кроме того, отмечается необходимость введения обобщенных критериев для выбора базового интервала для обработки.

Известен способ определения автоматизированной оценки в полете суммарной силы тяги двигателей летательного аппарата, пат. №2364846 от 14.03.08 г., включающий измерения самолетными датчиками - акселерометрами продольной и нормальной перегрузок в центре масс ЛА, скоростного напора, скорости полета ЛА в дискретные равноотстоящие моменты времени. При этом проводят измерения на неустановившихся режимах полета, в которых скоростной напор воздушного потока изменяется быстро по отношению к исходному в балансировочном режиме, в качестве которого принимают горизонтальный полет на заданной высоте. Определяют оценку суммарной тяги во время полета, используя аэродинамические соотношения вектора состояния ЛА, уравнение движения ЛА в продольной плоскости по осям координат с помощью ЭВМ.

Однако данный способ предполагает накопление измерений и уточнение оценок с приходом "новой" по времени информации, а "старая" информация не удаляется из матрицы, содержащей экспериментальные данные, поэтому интервал наблюдений расширяется, увеличиваются временные затраты на обращение матрицы, отсутствуют критерии для управления величиной базового интервала обработки, что снижает точность результатов идентификации аэродинамических характеристик ЛА.

Технический результат.

Технический результат, на создание которого направленно данное изобретение, заключается в увеличении достоверности описания математической модели движения летательного аппарата (ЛА), повышении точности оценок параметров математической модели (ММ) движения ЛА - аэродинамических коэффициентов за счет предложенного критерия оценки точности результатов идентификации, который используется для управления величиной базового интервала обработки, в сокращении временных затрат на обращение матрицы при уменьшении или увеличении базового интервала, а также в возможности применения в системах реального времени.

Существенные признаки.

Способ идентификации аэродинамических характеристик летательного аппарата по результатам испытаний, включающий проведение комплекса измерений параметров движения на неустановившихся режимах полета летательного аппарата (ЛА), обеспечение автоматического цифрового анализа измерительной информации, оценивание аэродинамических характеристик на основе идентификации математической модели движения ЛА на скользящем базовом интервале переменной длины, путем считывания последовательности измерений на скользящем базовом интервале - r, включающем (2l+1) измерений каждого из рассматриваемых параметров, представление их математической моделью из (2l+1) скалярных уравнений

S=ZC+ε,

где S - измеряемый вектор зависимой переменной, размерностью (2l+1)×1, Z - матрица измерений, состоящая из (2l+1) строк и m столбцов, C - вектор коэффициентов математической модели (MM), размерностью (m×1), ε - вектор невязок уравнений модели, размерностью (2l+1)×1, оценивание текущих значений коэффициентов C_r математической модели на r интервале, вводят скользящий базовый интервал переменной длины, изменяют интервал обработки путем исключения из рассмотрения наиболее «старой» по времени информации и добавления «новой», рассчитывают критерий точности вектора коэффициентов на измененном интервале, определяют промежуточный результат матрицы измерений , соответствующий расширению интервала обработки на одно измерение «справа», осуществляют переход матрицы Z_r к матрице добавлением одной строки, элементы которой относят к (r+l+1) измерению параметров (Z₁...Z_m), осуществляют переход от матрицы к матрице Z_r+1 путем исключения из матрицы первой строки, содержащей измерения параметров (Z₁…Z_m), относящиеся к (r-l) измерению, причем матрице Z_r соответствуют столбцы S_r и ε_r, содержащие (2l+1) элементов, производят вычисление текущей оценки , характеризующей оценку адекватности ММ реальному объекту при увеличении или уменьшении базового интервала, и принимают соответствующее решение о числе наблюдений на интервале,

,

где T - операция транспонирования;

проводят вычисления в рекуррентной постановке значений на скользящем базовом интервале фиксированной длины в следующей последовательности:

а) рассчитывают P_r и оценки , из условия минимума суммы квадратов невязок

,

,

,

где

,

,

tr - след матрицы,

б) добавляют "новую" информацию в момент времени (r+l+1) в матрицу измерений Z в виде строки α_r+l+1 и "новое" значение s_r+l+1 в вектор S и по формулам в рекуррентной постановке рассчитывают ,

в) удаляют "старую" информацию в момент времени (r-1) из матрицы измерений Z в виде строки α_r-1 и значение s_r-1 из вектора S и по формулам в рекуррентной постановке рассчитывают P_r+1, и , соответствующие перемещенному базовому интервалу на одно измерение,

,

,

,

каждое изменение интервала обработки (величины скользящего базового интервала) сопровождают вычислениями и , изменение интервала обработки осуществляют добавлением "новой" или удалением "старой" информации до тех пор пока не будет получено удовлетворительное совпадение достигнутых текущих оценок с допустимыми их значениями, заданными на основе экспертных знаний, затем по результатам сравнения выбирают величину базового интервала для обработки результатов измерений в системе реального времени.

Способ поясняется на чертежах.

Для пояснения сущности данного способа на фиг.1 приводится схема управления величиной скользящего базового интервала, где изображены:

1. Оценка параметров модели;

2. Расчет критерия

3. Уменьшение базового интервала;

4. Увеличение базового интервала;

5. Принятие решения;

6. Выбор величины базового интервала.

На фиг.2 представлены переходные процессы исходного экспериментального режима: нормальная перегрузка - n_y угловая скорость тангажа - ω_z, производная угловой скорости тангажа - , угол отклонения стабилизатора (поверхность управления в продольной плоскости ЛА) - φ_cm.

На фиг.3 приведены результаты оценивания коэффициентов аэродинамических моментов на скользящем базовом интервале фиксированной величины - , и в зависимости от - номера отсчета N (времени).

Способ реализуется следующим образом.

По результатам испытаний летательных аппаратов (ЛА) проводят измерения параметров испытаний системы, математическая модель которой состоит из 2l+1 скалярных уравнений

S=ZC+ε,

где S - измеряемый вектор зависимой переменной, размерностью (2l+1)×1, Z - матрица измерений, состоящая из (2l+1) строк и m столбцов, C - вектор коэффициентов математической модели (MM), размерностью (m×1), ε - вектор невязок уравнений модели, размерностью (2l+1)×1, оценивают текущие значения коэффициентов C_r математической модели на r интервале,

вводят скользящий базовый интервал переменной длины, содержащий (2l+1) измерений

,

где T - операция транспонирования.

Переход от матрицы Z_r к матрице осуществляют добавлением одной строки, элементы которой относятся к (r+l+1) измерению параметров (Z₁…Z_m).

- промежуточный результат, соответствующий расширению интервала обработки на одно измерение «справа».

Переход от матрицы к матрице Z_r+1 осуществляют путем исключения из матрицы первой строки измерения параметров (Z₁…Z_m), относящихся к (r-l) измерению.

Матрице Z_r соответствуют столбцы S_r и ε_r, содержащие по (2l+1) элементов. Рекуррентное оценивание на скользящем базовом интервале фиксированной длины проводят по следующим формулам:

где T - операция транспонирования; - оценка коэффициентов MM по методу наименьших квадратов; α - строка матрицы Z,

проводят рекуррентное вычисление на скользящем базовом интервале фиксированной длины текущей оценки в соответствии с формулами:

,

где

,

tr - след матрицы.

Адаптация базового интервала проходит поэтапно с расчетом показателя точности .

В случае существенного изменения параметров ММ при увеличении времени наблюдения вводят в рассмотрение скользящий базовый интервал (СБИ) переменной длины, адаптируемый к экспериментальным данным. Изменение информации на СБИ осуществляют путем исключения из рассмотрения наиболее «старой» (по времени) информации и добавления «новой». Изменение интервала обработки осуществляют на основе сравнения расчетной текущей оценки и допустимым ее значением , получаемым на основе экспертных знаний (см. фиг.1).

Рекуррентное вычисление текущих оценок , и на скользящем базовом интервале переменной длины при уменьшении базового интервала проводят по следующим формулам:

Рекуррентное вычисление текущих оценок и на скользящем базовом интервале переменной длины при увеличении базового интервала проводят по следующим формулам:

,

Величину скользящего базового интервала, на котором получена текущая оценка удовлетворяющая допустимому значению точности (см. фиг.1), используют в качестве величины базового интервала для дальнейшей обработки результатов измерений в системе реального времени.

Таким образом, предложенный способ обеспечивает повышение оценки точности результатов идентификации, сокращение временных затрат на обращение матрицы при уменьшении или увеличении базового интервала, а также в возможности применения в системах реального времени.

Пример.

Проводят в полете измерения параметров движения на неустановившемся режиме продольного короткопериодического движения самолета, см. фиг.2, на которой представлены переходные процессы исходного экспериментального режима:

нормальная перегрузка - n_y, угловая скорость тангажа - ω_z, производная угловой скорости тангажа - угол отклонения стабилизатора (поверхность управления в продольной плоскости ЛА) - φ_cm.

Экспериментальный режим соответствует уравнению продольного короткопериодического движения самолета в продольной плоскости в приращениях относительно установившегося прямолинейного горизонтального полета

где c₁, c₂ и с₃ - коэффициенты аэродинамических моментов,

Δn_y, Δω_z, Δφ_cm - приращение значений измеряемых параметров.

Далее уравнение записывают на базовом интервале r, содержащем 2l+1 измерение, в соответствии с заявленной математической моделью

S=ZC+ε,

где матрицы S, Z, C, s имеют следующий вид

В системе автоматизированной обработки проводят цифровой анализ измерений исходного экспериментального режима, оценивают аэродинамические характеристики ЛА по результатам испытаний в соответствии с предложенным способом идентификации с использованием приведенной выше математической модели движения ЛА. Определяют величину скользящего базового интервала на основе сравнения расчетных текущих оценок с допустимым ее значением (см. фиг.1). Получают величину скользящего базового интервала (для приведенного примера скользящий базовый интервал состоит из 64 равноотстоящих моментов времени). На скользящем базовом интервале постоянной длины получают следующие коэффициенты аэродинамического продольного момента

,

где

- производная коэффициента продольного момента m_z по углу атаки d;

- производная коэффициента продольного момента m_z по угловой скорости изменения угла атаки ;

- производная коэффициента продольного момента m_z по угловой скорости ω_z;

- производная коэффициента продольного момента m_z по углу отклонения стабилизатора φ_cm;

φ_cm - угол отклонения стабилизатора;

- производная коэффициента подъемной силы C_y по углу атаки α;

G - вес ЛА;

q - скоростной напор воздушного потока;

S - площадь крыла;

g - ускорение силы тяжести;

V - скорость полета;

b_a - средняя аэродинамическая хорда крыла,

J_z - момент инерции ЛА относительно оси координат z.

На фиг.3 приведены результаты оценивания коэффициентов аэродинамических моментов , и в зависимости от номера отсчета (времени).

Способ идентификации аэродинамических характеристик летательного аппарата по результатам испытаний, включающий проведение комплекса измерений параметров движения на неустановившихся режимах полета летательного аппарата (ЛА), обеспечение автоматического цифрового анализа измерительной информации, оценивание аэродинамических характеристик на основе идентификации математической модели движения ЛА на скользящем базовом интервале переменной длины, путем считывания последовательности измерений на скользящем базовом интервале - r, включающем (2l+1) измерений каждого из рассматриваемых параметров, представление их математической моделью из (2l+1) скалярных уравненийS=ZC+ε,где S - измеряемый вектор зависимой переменной с размерностью (2l+1)×1;Z - матрица измерений, состоящая из (2l+1) строк и m столбцов;С - вектор коэффициентов математической модели (ММ) с размерностью (m×1);ε - вектор невязок уравнений модели с размерностью (2l+1)×1,оценивание текущих значений коэффициентов C_r математической модели на r интервале, отличающийся тем, что вводят скользящий базовый интервал переменной длины, изменяют интервал обработки путем исключения из рассмотрения наиболее «старой» по времени информации и добавления «новой», рассчитывают критерий точности вектора коэффициентов на измененном интервале, определяют промежуточный результат матрицы измерений соответствующий расширению интервала обработки на одно измерение «справа», осуществляют переход матрицы Z_r к матрице добавлением одной строки, элементы которой относят к (r+l+1) измерению параметров (Z₁…Z_m), осуществляют переход от матрицы к матрице Z_r+1 путем исключения из матрицы первой строки, содержащей измерения параметров (Z₁…Z_m), относящиеся к (r-l) измерению, причем матрице Z_r соответствуют столбцы S_r и ε_r, содержащие (2l+1) элементов, производят вычисление текущей оценки , характеризующей оценку адекватности ММ реальному объекту при увеличении или уменьшении базового интервала, и принимают соответствующее решение о числе наблюдений на интервале, , гдеТ - операция транспонирования;проводят вычисления в рекуррентной постановке значений на скользящем базовом интервале фиксированной длины в следующей последовательности:рассчитывают P_r и оценки , из условия минимума суммы квадратов невязок , ,где , tr - след матрицы,добавляют "новую" информацию в момент времени (r+l+1) в матрицу измерений Z в виде строки α_r+l+1 "новое" значение s_r+l+1 в вектор S и по формулам в рекуррентной постановке рассчитывают , удаляют "старую" информацию в момент времени (r-1) из матрицы измерений Z в виде строки α_r-1 и значение s_r-1 из вектора S и по формулам в рекуррентной постановке рассчитывают P_r+1, и , соответствующие перемещенному базовому интервалу на одно измерение, , , , каждое изменение интервала обработки (величины скользящего базового интервала) сопровождают вычислениями и , изменение интервала обработки осуществляют добавлением "новой" или удалением "старой" информации до тех пор, пока не будет получено удовлетворительное совпадение достигнутых текущих оценок с допустимыми их значениями, заданными на основе экспертных знаний, затем по результатам сравнения выбирают величину базового интервала для обработки результатов измерений в системе реального времени.