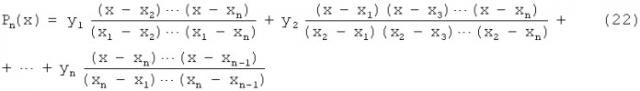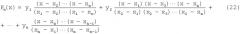Способ теплового контроля сопротивления теплопередаче многослойной конструкции в нестационарных условиях теплопередачи

Способ теплового контроля сопротивления теплопередаче многослойной конструкции в нестационарных условиях теплопередачи

Иллюстрации

Показать все

Реферат

Изобретение относится к области измерительной техники, в частности к тепловому неразрушающему контролю объектов, и может быть использовано для технической диагностики неоднородных конструкций, например, зданий и сооружений по сопротивлению теплопроводности.

Из уровня техники известны способы теплового неразрушающего контроля неоднородных многослойных объектов, какими, в частности, являются здания и сооружения, см. патент РФ №2219534. Для осуществления известного способа определяют временной интервал, необходимый для получения достоверного результата. В течение этого времени периодически измеряют температуру и плотность теплового потока на наружной и внутренней поверхностях объекта. Задают значение теплопроводности нужного слоя. Используя модель, определяют возможную температуру и плотность для каждого заданного значения теплопроводности. Проводят тепловизионное обследование, измеряют температуры внутренних и наружных поверхностей. Сравнивают теоретические и полученные измерением результаты. Выбирают для дальнейших расчетов значение теплопроводности из числа заданных, которое может обеспечить условия сравнения. Способ позволяет определить локальные сопротивления теплопередаче обследуемых участков и найти более рациональное решение по обеспечению требуемого сопротивления, если оно окажется не соответствующим нормативному.

Однако известный способ не применим для исследования нестационарных процессов, имеющих место в реальных условиях эксплуатации зданий и сооружений.

В Российской Федерации на практике используется способ определения качества объектов по анализу их сопротивления теплопередаче - см. ГОСТ 26254-84. Здания и сооружения. Методы определения сопротивления теплопередаче ограждающих конструкций. Введен постановлением Государственного комитета СССР по делам строительства от 2 августа 1984 года №127, УДК 624.01.001.006.354[1]. Описанный здесь способ заключается в создании теплового потока через контролируемый объект, одномоментном измерении величины теплового потока (q) и температуры (Tн, Tв) на противоположных сторонах контролируемого объекта и определении качества объекта по его сопротивлению теплопередаче в соответствии с формулой

Данный метод контроля прост, нагляден, имеет большую производительность. Однако имеет недостаток, который ограничивает область его применения и значительно снижает точность получаемых результатов. Он заключается в том, что в соответствии с классическим определением сопротивления теплопередаче, метод применим только при условии стационарного процесса теплопередачи через контролируемый объект. Т.е. только при условии равенства потоков, входящих в объект на одной поверхности qн и выходящих qв из объекта на другой поверхности: qн=qв=q.

На практике эти условия практически никогда не соблюдаются. Например, при контроле строительных конструкций разница температуры наружного воздуха в ночное и дневное время достигает 10-15 град.С. Это вызывает нестационарные процессы теплопередачи в исследуемых конструкциях и делает метод неприменимым.

Решение этой проблемы предложено в монографии Будадин О.Н. и др. Тепловой неразрушающий контроль изделий. М.: Наука, 2002, с.139-145. Оно заключается в решении обратной задачи нестационарной теплопроводности в многослойной среде. Метод универсален и в настоящее время находит широкое применение на практике. Однако широкое его применение сдерживается рядом недостатков, которые заключаются в следующем:

- имеется существенная нелинейная зависимость точности получаемых результатов от погрешности входных данных - результатов первичных измерений. Это приводит к необходимости обеспечивать малые значения погрешности результатов первичных измерений, что требует применения специальных измерительных приборов, квалифицированных операторов и т.п. Помимо этого требуется соблюдение специальных климатических условий при проведении измерений;

- наличие ошибки входных данных может привести к случаю, когда обратная задача не сходится, т.е. будет отсутствовать решение;

- решением обратной задачи, как правило, является не само сопротивление теплопередаче, а величина теплопроводности одного из слоев, обычно слоя с наименьшим сопротивлением теплопередаче - теплоизоляционного слоя;

- в результате решения обратной задачи в силу специфических особенностей математического аппарата и физических принципов получаются кроме основного решения (глобального минимума функции «невязки») несколько локальных минимумов (ложных решений). Это приводит к необходимости выбора нужного «истинного» решения на основе других дополнительных входных данных и др.;

- перед применением метода обратной задачи необходимо провести цикл трудоемких исследований корректности, единственности, сходимости и устойчивости решения.

Изобретение направлено на устранение перечисленных недостатков.

Технический результат, достигаемый при его использовании по сравнению с ближайшим аналогом - способом по патенту РФ №2219534, заключается в повышении достоверности и производительности определения качества исследуемого объекта в нестационарных условиях теплопередачи.

Технический результат достигается за счет того, что в способе теплового контроля сопротивления теплопередаче многослойной конструкции в нестационарных условиях теплопередачи, включающем тепловизионное обследование одной из поверхностей исследуемого объекта, сравнение теоретических и полученных измерением результатов и выбор для дальнейших расчетов значения теплопроводности из числа заданных, которое может обеспечить условия сравнения, перед тепловизионным обследованием конструкции определяют время тепловой инерции теплопередачи, а также дискретность разрешения тепловизора, исходя из минимального дефекта, тепловизионное обследование проводят путем измерения температурного поля T(x, y) поверхности с пространственным периодом (шагом - Δa), определяемым размерами минимального дефекта конструкции:

где Δx_дmin, Δy_дmin - геометрические размеры минимального дефекта контролируемой конструкции,

- измеряют значения температуры T_н(t_i), T_в(t_i) на противоположных сторонах конструкции в области с координатами контура L(x, y) вблизи точки с координатами x₀, y₀, с временными интервалами τ_тн и τ_тв, соответственно, в течение интервалов времени:

а) на наружной поверхности Δτ_из ^нар=(0…τ_из), на внутренней поверхности Δτ_из ^вн=(Δτ_ин…(Δτ_ин+τ_из));

б) измеряют значения теплового потока на внутренней стороне конструкции q_в(t_j) с временным интервалом τ_q последовательно во времени в течение интервала времени Δτ_из ^вн=(Δτ_ин…(Δτ_ин+τ_из));

- накапливают по каждому измерению значения температуры T_н(t_i), T_в(t_i) на противоположных сторонах конструкции и значения теплового потока q_в(t_j),

- определяют сопротивление теплопередаче (R) многослойной конструкции в точке контролируемого участка поверхности исследуемого объекта с координатами (x₀, y₀):

где N₁ = (целое число) от Δτ_из ^вн/τ_тв,

N₂ = (целое число) от τ_из/τ_тн,

N₃ = (целое число) от Δτ_из ^вн/τ_q,

i, j, k - индексы суммирования, и определяют термическое сопротивление по всей поверхности исследуемого объекта в произвольных координатах (x, y):

R(x, y)=aT(х, y)+b,

где

a=[R(x₀₁, y₀₁)-R(x₀₂, y₀₂]/[T(x₀₁, y₀₁)-T(x₀₂, У₀₂)]

b=R(x₀₁, y₀₁)-aT(x₀₁, y₀₁).

Технический результат усиливается за счет того, что геометрические размеры минимального дефекта контролируемой конструкции Δx_дmin, Δy_дmin измеряют следующим образом:

- производят послойную препарацию образцов контролируемой конструкции,

- измеряют размеры всех дефектов, содержащихся в образце, выявленных в результате препарации: Δx_дi, Δy_дi,

- определяют размеры минимального дефекта контролируемой конструкции (Δx_дmin, Δy_дmin), решая систему уравнений:

где

δ - вероятность того, что (Δx_дi, Δy_дi)≥(Δx_дmin, Δy_дmin);

p(ΔX_i) - функция распределения величин Δx_дi, Δy_дi.

Координаты контура на поверхности контролируемого объекта определяют следующим образом:

- измеряют разброс температурного поля по различным участкам исследуемой поверхности по результатам тепловизионного обследования с точностью, определяемой величиной изменения температуры (ΔTдеф), обусловленной минимальным дефектом конструкции,

- по результатам проведенных измерений определяют те участки поверхности L(x, y), в области которых выполняется условие:

где

L(x, y) - контур области,

(x, y) - координаты контура области,

Tмах - наибольшая температура внутри области L(x, y),

Tmin - наименьшая температура внутри области L(x, y),

ΔTдеф - изменение температуры поверхности, обусловленной минимальным дефектом,

Dуч - размер участка L(x, y) по исследуемой поверхности,

Hконстр - толщина исследуемой конструкции,

Hконстр=H₁+H₂+…+H_n,

n - количество слоев конструкции.

Временной интервал проведения измерений температуры и теплового потока в области определенных участков L(x, y) в точке с координатами (x₀, y₀) определяют путем измерения времени тепловой инерции (τ_ин) исследуемой конструкции, измеряя время прохождения теплового импульса между поверхностями конструкции.

Оптимальный интервал последовательного измерения температуры (τ_тн) (τ_тв) и теплового потока (τ_q) на исследуемой конструкции определяют путем решения уравнения

f(T) - плотность распределения длительности во времени информационного сигнала,

τ - временной интервал измерения,

P - вероятность пропуска информационного сигнала

T₀ - временная разрешающая способность измерительных датчиков,

η - текущая переменная.

Температурные поля и тепловой поток измеряют измерителем температуры самопишущим или электронным измерителем плотности тепловых потоков, пятиканальным или тепловым зондом.

Координаты (x₀, y₀) определяются путем решения системы уравнений:

Проводят тепловизионное обследование наружной поверхности исследуемого объекта.

Время прохождения теплового импульса между поверхностями конструкции определяют путем расчетов, исходя из теплотехнических характеристик материалов слоев конструкции, по формуле

где k_n - определяется из решения уравнения

Fo - критериальное число Фурье;

y - безразмерная координата пластины;

Bi - критерий Био,

n - индекс суммирования.

Сущность изобретения и возможность достижения технического результата будут более понятны из последующего описания со ссылками на позиции чертежей.

На фиг.1 приведены фотографии конструкций с реальными дефектами в виде областей нарушения сплошности (расслоения).

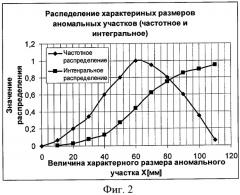
На фиг.2 приведены, в качестве примера, гистограммы распределения размеров областей нарушения сплошности p(ΔX_i). Таким образом осуществляется измерение геометрических размеров минимального дефекта контролируемой конструкции Δx_дmin, Δy_дmin.

На фиг.3 приведена, в качестве примера, термограмма одной из поверхностей исследуемого объекта.

На фиг.4 приведена функциональная схема регистрации термограммы для измерения температурного поля T(x, y).

На фиг.5 отмечен контур области L(x, y).

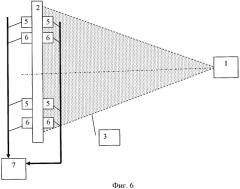
На фиг.6 показана схема проведения экспериментальных исследований.

На фиг.7 (а, б) приведены реальные реализации во времени температуры на наружной и внутренней поверхностях многослойной конструкции.

На фиг.8 приведен состав конструкции, на которой проводились экспериментальные исследования с теплотехническими и геометрическими характеристиками слоев.

На фиг.9 приведен график прогрева (распространения теплового фронта) контролируемого объекта.

На фиг.10 приведен состав конструкции для модельного эксперимента.

На фиг.11 приведены в виде графиков результаты модельного эксперимента.

На фигурах приняты следующие обозначения:

1 - тепловизионная система,

2 - объект контроля - многослойная конструкция,

3 - поле обзора тепловизионной системы,

4 - мгновенной линейное поле зрения (геометрическая разрешающая способность) тепловизионной системы,

5 - контактные микропроцессорные контактные преобразователи температуры (датчики температуры),

6 - контактные микропроцессорные контактные преобразователи теплового потока (датчики теплового потока),

7 - электронный блок сбора и обработки информации,

A_деф - размеры минимального дефекта ((геометрическая разрешающая способность),

S - расстояние от тепловизионной системы до объекта контроля,

L - толщина исследуемого слоя,

t₁, t₂, t₃, t₄ и t₅ - моменты времени, характеризующие температурные распределения в слое толщиной L,

X₁, Х₂, Х₃, X₄ и L - значения глубины прогрева, соответствующие моментам времени t₁, t₂, t₃, t₄ и t₅,

Tc - температура среды (воздуха) на внешней поверхности,

Tнар.пов. - температура на наружной поверхности,

Tвн.пов. - температура на внутренней поверхности,

Tв - температура среды (воздуха) на внутренней поверхности,

qвнутр - плотность теплового потока на внутренней поверхности,

qнаружн - плотность теплового потока на наружной поверхности,

Δτ_ин - время тепловой инерции конструкции.

Время прохождения теплового импульса между поверхностями конструкции возможно определять расчетным способом исходя из теплотехнических характеристик материалов слоев конструкции. Это может быть осуществлено, например, следующим образом.

Примем физическую модель рассматриваемого объекта в виде однородной неограниченной пластины шириной L. В начальный момент времени внутренняя поверхность пластины вводится в соприкосновение с источником тепловой мощности с температурой t_c1.

Введем следующие ограничения:

1. Соприкосновение источника тепловой мощности с нагреваемым участком поверхности исследуемого объекта осуществляется столь быстро, что данный процесс соприкосновения можно считать мгновенным.

2. Температура источника тепловой мощности с начала и до конца процесса остается неизменной.

3. Тепловая мощность источника постоянна в течение всего процесса.

4. Протяженность источника тепловой мощности вдоль поверхности исследуемого объекта много больше, чем толщина исследуемого объекта.

Указанным ограничениям в наилучшей степени удовлетворяет компактный проточный теплообменник, тепловая инерционность которого значительно меньше тепловой инерционности исследуемого объекта.

Введем также следующие допущения:

1. Тепловой поток через исследуемый объект одномерный и однородный по сечению.

2. Теплофизические параметры материала исследуемого объекта постоянны.

3. Коэффициент теплоотдачи от источника к прилегающей поверхности исследуемого объекта остается неизменным в любой момент времени.

4. Вплоть до завершения первой стадии нестационарного теплового режима внешнюю (противоположную соприкасающейся с источником тепла) поверхность исследуемого объекта можно считать теплоизолированной.

Математическая модель описываемого объекта в рамках описанной физической модели может быть представлена краевой задачей, включающей уравнение теплопроводности

с граничными условиями

и начальным условием

где t - температура пластины; θ - время [c].

Введем безразмерные переменные

где Fo - критериальное число Фурье; y - безразмерная координата пластины;

Bi - критерий Био; θ - безразмерная температура пластины.

Преобразуем (1-4) к виду

Решим задачу методом разделения переменных. Представим температуру как произведение двух функций, первая из которых зависит только от переменной у, а вторая - только от переменной Fo.

После подстановки (10 в (6)-(9) задача распадется на две.

1)

где k - введенный нами параметр.

2)

Решение уравнения (11) будет равно

Подставим (15) в (12) и (13), тогда

kA=0⇒A=0, Y(y)=B cos ky при y=0,

- kB sin k=-BiB cos k при y=1.

Отсюда получим

Это трансцендентное уравнение имеет бесчисленное множество корней и может быть решено графически или численно.

С учетом решения уравнения (14) запишем общее решение как сумму всех частных решений

Постоянные C_n могут быть определены из начального условия (13)

где

Тогда, с учетом (18)-(20), перепишем (17)

Выражение (21) с учетом (5) позволяет вычислить распределение температуры в пластине в любой момент времени при данных теплофизических свойствах пластины и среды.

В качестве примера (фиг.3) приведена термограмма одной из поверхностей исследуемого объекта. Данная термограмма зарегистрирована с пространственным периодом (шагом - Δа), определяемым размерами минимального дефекта конструкции:

На основе данной термограммы измеряют температурное поле T(x, y) исследуемой поверхности.

На фиг.4 приведена функциональная схема регистрации термограммы для измерения температурного поля T(x, y). Регистрация осуществляется следующим образом.

Тепловизионная система размещается перед контролируемой поверхностью на расстоянии, обеспечивающем:

- во первых - одновременное наблюдение максимальной площади контролируемой поверхности с учетом поля обзора тепловизионной системы,

- во-вторых - достоверную регистрацию минимального по размерам локального участка изменения температуры (возможного дефектного участка) поверхности контролируемой поверхности.

При этих условиях расстояние от тепловизионной системы до контролируемой поверхности определяется следующим образом:

S≥Aдеф/(2Ntg(γ/2)),

где S - расстояние от тепловизионной системы до фурменной зоны,

Aдеф - характерный размер участка с локальным изменением температуры (дефектный участок),

N - коэффициент, определяющий достоверность регистрации локального участка (обычно на практике принимают N=3-10),

γ - угол мгновенного линейного поля зрения оптической системы тепловизионного прибора (угловая разрешающая способность. Обычно, на практике, γ=5-10 угл. мин),

tg - тригонометрическая функция «тангенс».

По результатам измерения температурного поля T(x, y) исследуемой поверхности измеряют разброс температурного поля по различным участкам исследуемой поверхности с точностью, определяемой величиной изменения температуры (ΔTдеф), обусловленной минимальным дефектом конструкции, и температурного поля T(x, y) исследуемой поверхности. Определяют координаты контура поверхности L(x, y), в области которых выполняется условие:

где

L(x, y) - контур области,

(x, y) - координаты контура области,

Tмах - наибольшая температура внутри области L(x, y),

Tmin - наименьшая температура внутри области L(x, y),

ΔTдеф - изменение температуры поверхности, обусловленной минимальным дефектом,

Dуч - размер участка L(x, y) по исследуемой поверхности,

Hконстр - толщина исследуемой конструкции,

Hконстр=H₁+H₂+…+H_n,

n - количество слоев конструкции,

Температурные поля и теплововй поток измеряют с использованием измерителя самопишущего ИС-203.2 ООО «ТехноАс», г.Коломна, Электронного измерителя плотности тепловых потоков пятиканального ИТП-МГ4.03 «ПОТОК» и зондов, выпускаемых ООО «Стройприбор», г.Челябинск.

На фиг.5 отмечен контур области L(x, y). Координаты контура определяются, например, с использованием математических моделей построения по точкам и воспроизведения кривых.

Анализ формы объектов представляет собой одну из основных задач распознавания образов и имеет определенное значение для решения задач машинной графики в интерактивном режиме. Анализ формы оказывается полезным во всех случаях, когда требуется принять некоторое решение на основе формы наблюдаемых объектов.

Рассмотрим два подхода к распознаванию формы объектов.

При использовании первого подхода рассматриваем объект в целом и принимаем решение, исходя из его общей структуры.

При втором подходе исследуется контур силуэта: обычно определяются углы, выступы, впадины и другие точки с высокими значениями кривизны.

Дальнейший анализ контура проводится несколькими способами. Простейшая методология предусматривает получение несложного представления контура, например, в цепном коде. При использовании более развитой методологии контур аппроксимируется участками гладких кривых (например, В-сплайнами). Последнее предпочтительно в тех случаях, когда данные зашумлены, а также при использовании признаков, отражающих особенности значительной части контура. Первый подход более уместен при работе с данными, отличающимися низким уровнем шума, и использовании локальных признаков. Широкое применение аппроксимации многоугольниками объясняется не только связанной с ней возможностью обнаруживать максимумы кривизны, но и тем, что ее реализация оказывается проще реализации других методов построения кривых по точкам.

Отыскание кривой, проходящей через заданное множество точек, составляет задачу интерполирования, а отыскание кривой, проходящей вблизи заданного множества точек - задачу аппроксимации. Разработан метод, предусматривающий использование кусочно-полиномиальных функций различных типов. При решении задач аппроксимации уделяется внимание выбору критерия, характеризующего качество приближения.

Для решения поставленной задачи разработан метод интерполирования с помощью многочленов.

Пусть (x₁, y₁), (x₂, y₂), …, (x_n, y_n) - последовательность точек, заданных на плоскости, причем x=x при i=j. Для таких точек можно непосредственно написать формулу интерполяционного многочлена (n-1)-ной степени:

интерполяционный многочлен можно представить в более строгом виде:

Из приведенного выражения следует, что значение y умножается на дробь, равную 1 при x=x и 0 при остальных значениях x, принимаемых им в заданных координатах. Частному случаю n=2 соответствует уравнение линии, соединяющей две точки:

Определяют геометрические координаты точки (x₀, y₀) области L(x, y) путем решения системы уравнений:

В районе центра определенных участков L(x, y) с координатами (x₀, y₀) устанавливают на наружной и внутренней поверхностях датчики температуры и теплового потока, которые с определенным выше временным интервалом регистрируют и сохраняют в памяти значения температуры и теплового потока. При этом количество датчиков практически не ограничено.

На фиг.6 показана схема проведения экспериментальных исследований и состав конструкции с теплотехническими и геометрическими характеристиками.

На наружную и внутреннюю поверхность контролируемого изделия (2) устанавливаются датчики температуры и теплового потока (5, 6), которые в течение заданного времени (времени тепловой инерции контролируемого объекта) - τ_ин регистрируют с периодом (τ_и), значения температуры T_н(t), T_в(t) на противоположных сторонах конструкции и теплового потока q_в(t) - значения теплового потока на внутренней поверхности. Датчики устанавливаются по всей выделенной области L(x, y) в близи точки с координатами (x₀, y₀). В качестве примера, некоторые реализации представлены на фиг.7. Под наружной поверхностью конструкции будем понимать поверхность, обращенную к внешней климатической среде. Измеренные значения температур и теплового потока собираются и суммируются в блоке (7).

В блоке (7) определятся сопротивление теплопередачи (R) многослойной конструкции в точке контролируемого участка поверхности исследуемого объекта с координатами (x₀, y₀):

где N₁ = (целое число) от Δτ_из ^вн/τ_тв,

N₂ = (целое число) от τ_из/τ_тн,

N₃ = (целое число) от Δτ_из ^вн/τ_q,

i, j, k - индексы суммирования,

На фиг.7 приведены экспериментальные, полученные с реальной многослойной конструкции, временные истории (значения в различные последовательные моменты времени) температуры и теплового потока, замеренные на поверхности.

На фиг.8 - приведен состав многослойной конструкции на которой проводились экспериментальные исследования с теплотехническими и геометрическими характеристиками слоев.

Далее осуществляется регистрация температурного поля T(x, y) с поверхности контролируемого объекта (фиг.3)

На основе измеренного температурного поля T(x, y) определяют термическое сопротивление по всей поверхности исследуемого объекта в произвольных координатах (x, y):

R(x, y)=aT(x, y)+b,

где

a=[R(x₀₁, y₀₁)-R(x₀₂, y₀₂]/[T(x₀₁, y₀₁)-T(x₀₂, y₀₂)];

b=R(x₀₁, y₀₁)-aT(x₀₁, y₀₁).

Процесс прогрева плоского слоя изображен на фиг.9, где по оси абсцисс отложено расстояние от внутренней поверхности исследуемого объекта до определенной точки внутри исследуемого объекта, а по оси ординат - температура в этой точке. На фиг.9 каждому моменту времени t_i соответствует своя координата X_i, больше которой слой материала остается изотермическим и сохраняющим начальную температуру, в то время как в пределах изменения координаты 0≤X<X_i температурное поле уже выше начального. В пределах этого слоя 0≤X<X_i температура убывает от значения T_i до T₀. На фиг.9 представлено пять линий, характеризующих температурные распределения в слое толщиной L для моментов времени t₁, t₂, t₃, t₄ и t₅. Соответствующие этим моментам времени значения глубины прогрева составляют соответственно X₁, X₂, Х₃, Х₄ и L. Поскольку L соответствует полной толщине исследуемого слоя, то момент времени t₅ соответствует длительности полного нагрева исследуемого слоя.

Таким образом, на основе рассмотренной модели можно вычислить время прогрева с любой заданной точностью. В качестве примера примем, что время прогрева наступило, если температура на изолированной поверхности равна t=t₀+Δt₃, где 0.01°C≤Δt₃≤2°C. Это будет соответствовать значению числа Фурье Fo₁. Выбор диапазона предварителен и соответствует априорному представлению о чувствительности применяемой методики измерений температур.

Для обоснования предлагаемого способа проведен модельный (численный) эксперимент. Он заключается в следующем.

Моделируется процесс контроля трехслойной конструкции, состав и характеристики которой приведены на фиг.10.

В соответствии с формулой определялось время тепловой инерции конструкции. Для этого на одной из поверхностей моделировался температурный перепад (фиг.11) и рассчитывалась зависимость температурного фронта на противоположной стороне от времени (фиг.11). Из фиг.11 видно, что время инерции составляет, ориентировочно, Δτ_ин=25 часов. Далее на стороне, которую примем за наружную, моделировались суточные колебания температуры в виде синусоидальных колебаний с трендом в виде повышения температуры на 4°C в сутки. Рассчитывались значения температуры и теплового потока на внутренней поверхности в течение 4-х суток. Результаты моделирования в виде графиков приведены на фиг.11.

Расчет сопротивления теплопередаче в соответствии с заявляемой формулой показал, что R=3,145. Учитывая, что расчетное значение сопротивления теплопередаче на основании известных геометрических и теплофизических характеристик слоев составляет R_расч=3,08, ошибка модельного эксперимента составляет 1,8%, что вполне сопоставимо с погрешностью практических измерений и достаточно для практического применения.

Проведен натурный эксперимент определения сопротивления теплопередаче реальной стены строительной конструкции в реальных климатических условиях (фиг.8, 9).

В таблице 1 приведены сравнительные характеристики значения сопротивления теплопередаче в реперной зоне, определенные в соответствии с заявляемым способом и ближайшим аналогом и рассчитанные на основании конструкции стены (фиг.8). Также в таблице 1 приведена погрешность определения сопротивления теплопередаче (R) в соответствии с настоящим изобретением и ближайшим аналогом по сравнению с величиной, рассчитанной на основании конструкции стены по известной формуле:

где i - номер слоя многослойной конструкции,

δ - толщина i-го слоя,

λ - теплопроводность материала i-го слоя,

P - количество слоев.

Таблица 1.
№№ п/п	Способ определения величины сопротивления теплопередаче	Значения величины сопротивления теплопередаче	Погрешность (%) относительно п.3	Примечание
1	2	3	4	5
1	Изобретение	0,68	4,2%
2	Известный способ (ближайший аналог)	0,92	29,6%
3	Способ на основании прямого расчета по известным теплотехническим и геометрическим характеристикам конструкции	0,71

Отличие определенного сопротивления теплопередаче от истинного, определенного на основании известных теплотехнических и геометрических характеристик слоев строительной конструкции, обусловлено наличием случайных шумов и помех, содержащихся в экспериментальных данных. Возможно снижение погрешности (менее 4,2%) за счет применения специальных методов шумоподавления (например, методов фильтрации).

Результаты расширенного сравнения эксплуатационных и технических характеристик способов: заявляемого, принятого в качестве прототипа и принятого в качестве аналога приведены в таблице 2.

Таблица 2.
№ пп	Параметр	Численные значения параметра
Способ по предлагаемому изобретение	Способ - ближайший аналог	Способ-аналог
1	2	3	4	5
1	Определение сопротивления теплопередаче	Оперативный точный метод	Путем решения обратной задачи - метод трудоемкий и неоднозначный	Контроль без учета нестационарности процесса - погрешность до 100%
2	Погрешность результатов контроля	Не более 5% (возможно снижение погрешности до 3%)	До 30% (снижение погрешности практически невозможно)	До 100% (снижение погрешности принципиально невозможно)
3	Однозначность получаемых результатов контроля	Метод обеспечивает единственность решения (результата)	Возможно (вероятность 30%) вторичные решения - локальные минимумы	Метод обеспечивает единственный результат, но с недопустимой погрешностью (100%)
4	Допустимая погрешность входных данных	До 15%	До 5%	До 5%
5	Квалификация оператора	Средняя и низкая (на уровне среднетехнического образования)	Высокая (один из операторов - расчетчик должен иметь высшее образование)	Не определяется
6	Производительность контроля	Съем информации - 3 день(определяется временем	Съем информации - 3-7 дн.	Не определяется

		тепловой инерции конструкции). Расчет - 15 мин.	Расчет - 1 день.
7	Трудоемкость контроля	2 чел. (съем информации и расчет)	3 человека: 2 чел. - съем информации, 1 чел. - расчет.	Не определяется
8	Достоверность определения показателя назначения	Не менее 0,99 (определяется погрешностью входных данных)	0,7-0,85 (определяется погрешностью входных данных, градиентом метода «невязки», наличием локальных минимумов и т.п.)	Не определяется
9	Вероятность отсутствия решения	Отсутствует	Имеется вследствие величины погрешности входных данных	Не определяется
10	Вычислительные мощности и сложность математического аппарата	Низкие	Высокая из-за необходимости решения обратной задачи нестационарной теплопроводности	Не определяется

Подтверждено, что изобретение обеспечивает следующие технические преимущества перед аналогами:

- позволяет оперативно оценить качество контролируемых объектов, регистрировать это для оформления юридических документов (акта приемки-сдачи работ субподрядных организаций и т.д.) и последующего анализа причин несоответствия фактического состояния объектов их нормативным значениям и сокращает время ремонта, например, за счет сокращения сроков оперативного контроля качества ремонта, и повышает качество ремонта за счет повышения ответственности исполнителя работы;

- значительно повышает (до 99%) достоверность результатов контроля технического состояния строительных объектов (выявления дефектов и энергоэффективность);

- снижает возможность аварий строительных конструкций (нет данных) за счет своевременного выявления дефектов;

- повышает надежность эксплуатации строительных объектов (с последующим выходом на определение остаточного ресурса и рекомендации по повышению надежности эксплуатации);

- обеспечивает прогрессивное развитие бесконтактных способов контроля и автоматизации выявления (диагностики) дефектов в строительных конструкциях.

1. Способ теплового контроля сопротивления теплопередаче многослойной конструкции в нестационарных условиях теплопередачи, включающий тепловизионное обследование одной из поверхностей исследуемого объекта, отличающийся тем, что перед тепловизионным обследованием конструкции определяют время тепловой инерции (Δτ_ин) и дискретность разрешения тепловизора, и проводят тепловизионное обследование одной из поверхностей, исходя из размеров минимального дефекта путем измерения температурного поля Т(х, y) поверхности с пространственным периодом Δа, определяемым размерами минимального дефекта конструкции: где Δх_дmin, Δy_дmin - геометриче