Способ опредения составов нонвариантных равновесных фаз многокомпонентных водно-солевых систем

Способ опредения составов нонвариантных равновесных фаз многокомпонентных водно-солевых систем

Иллюстрации

Показать все

Реферат

Область техники.

Изобретение относится к области применения физико-химического анализа для определения составов нонвариантных равновесных фаз при изучении растворимости в многокомпонентных водно-солевых системах при постоянной температуре.

Уровень техники

Известны изотермические методы определения составов равновесных фаз в водно-солевых системах [Аносов В.Я., Погодин С.А. Основные начала физико-химического анализа. М.-Л.: Изд-во АН СССР, 1947; Аносов В.Я., Озерова М.И., Фиалков Ю.А. Основы физико-химического анализа. М.: Наука, 1976], такие как метод сечения [Никурашина Н.И., Мерцлин Р.В. Метод сечений, приложение его к изучению многофазного состояния многокомпонентных систем. Саратов: Изд-во Саратов, ун-та, 1969] и прогностический метод [Мазунин С.А. Основы физико-химического анализа: Учеб. пособие по спецкурсу / Перм. ун-т. - Пермь, 2000. - Ч.2. Многокомпонентные водно-солевые системы.], которые позволяют определить состав равновесной жидкой фазы, вычислить оптимальный состав исходной смеси компонентов (далее ИСК), соотношение исходных компонентов в донной фазе по составам равновесной жидкой фазы и ИСК, используя математические уравнения.

Наиболее близким аналогом для заявляемого способа является комбинированный метод изучения изотерм растворимости трех- и более компонентных водно-солевых систем эвтонического или перитонического типов, включающий математическое прогнозирование состава нонвариантного раствора по максимальным содержаниям солевых компонентов в нонвариантных растворах оконтуривающих систем, экспериментальное определение химическим анализом составов нонвариантных равновесных жидких фаз, образующихся из исходных смесей компонентов оптимального состава, измерения легко определяемого физического свойства жидкой фазы после установления равновесия в известных исходных смесях компонентов, располагающихся строго по изогидрическим сечениям фигуры состава, построение графиков "состав-свойство" и определения составов не менее двух точек на всех границах фазовых областей.

Твердые фазы, насыщающие нонвариантные растворы, устанавливают по точкам пересечения предельных нод, приходящих в одну и ту же твердую фазу, задаваемых координатами, экспериментально определенных составов нонвариантных жидких фаз, границ в оконтуривающих системах и вершин нонвариантных областей изогидрических разрезов системы без изоляции, разделения и дополнительной идентификации составных частей донных фаз. При этом ориентация границ нонвариантной области к сторонам солевой (безводной) концентрационной фигуры разреза позволяет определить тип фазового взаимодействия в системе. Параллельность этих границ сторонам концентрационной фигуры изогидрического разреза свидетельствует о кристаллизации из нонвариантного раствора безводных солевых компонентов. Не параллельность границ нонвариантной области сторонам концентрационной фигуры изогидрического разреза свидетельствует об образовании новой твердой фазы или кристаллогидратов в системе.

При наличии новой твердой фазы исходную систему триангулируют на ряд подсистем, включающих новую твердую фазу как исходных компонент. Изучение нонвариантных составов равновесных фаз в подсистемах проводят в той же указанной выше последовательности. [Мазунин С.А., Фролова С.И., Кистанова Н.С. Пат. 2324933 (2007) // БИ 2008, №14].

Данный метод не позволяет при увеличении числа компонентов в системах определить составы нонвариантных растворов с одинаковой точностью в связи с добавлением количества ионов и увеличением суммарной аналитической погрешности их определений. Кроме того, установленные составы равновесных твердых фаз в рамках комбинированного метода также имеют некоторые существенные погрешности и не исключают образование ограниченного ряда твердых растворов [Мазунин С.А., Фролова С.И., Кистанова Н.С. Пат. 2324932 (2007) // БИ 2008, №14].

Раскрытие изобретения

Задачей создания изобретения является получение на основе математического прогнозирования нонвариантного раствора надежных экспериментальных данных о составах нонвариантных равновесных фаз в многокомпонентных водно-солевых системах и их оптимальных разрезах без уменьшения точности с увеличением числа компонентов в системах и уменьшение трудоемкости экспериментальных операций.

Поставленная задача является первоочередной и решается с помощью признаков, указанных в формуле изобретения, общих с прототипом, таких как математическое прогнозирование состава нонвариантного раствора и определение направлений оптимальных сечений и разрезов, экспериментальное установление составов на всех границах нонвариантной области, измерением легко определяемого физического свойства жидкой фазы после установления равновесия в известных ИСК, располагающихся строго по сечениям фигуры состава и построения графиков "состав-свойство".

Отличительные существенные признаки заключаются в следующем. Предлагаемый способ предназначен для четырех- и более компонентных систем и позволяет исключить химический способ определения составов нонвариантных жидких фаз. Математическое прогнозирование нонвариантного раствора последовательным вычислением промежуточных составов по данным о содержании воды в нонвариантных растворах оконтуривающих систем, вычисление которых осуществляется по уравнению прямой, соединяющей составы нонвариантных растворов от максимального содержания воды через промежуточные составы к более меньшим, позволяет выбрать направления оптимальных сечений и разрезов для исследования границ нонвариантной области, посредством перспективного проецирования предполагаемого состава нонвариантного раствора из углов солевых компонентов на противолежащие оконтуривающие грани. Эти проекции определяют составы гомогенных растворов в оконтуривающих системах, добавление к которым одной твердой фазы, не содержащейся в растворе, образуют направления оптимальных сечений, ИСК которых готовятся двумя взвешиваниями. Исследования этих сечений дают наиболее точные результаты определения составов произвольно расположенных реперных точках на всех гранях нонвариантной области. Если проекции предполагаемого состава нонвариантного раствора находятся в гетерогенных областях оконтуривающих систем, исследуются изогидрические разрезы, ИСК в которых составляют тремя взвешиваниями из раствора и двух солей. По составам не менее двух реперных точек на каждой границе нонвариантной области вычисляют основные коэффициенты, равные отношениям содержаний компонента, который отсутствует в составах равновесных твердых фаз на соответствующих плоскостях или предельных нодах нонвариантной области системы, к содержанию воды. Сопоставляя относительно друг друга отличия коэффициентов, лежащих на одной границе, и определив, что они не превышают нескольких тысячных долей единицы, считают, что их составы выражены в истинной системе координат, вычисляют средние значения коэффициентов на каждой границе, а по ним состав нонвариантного раствора и подтверждают равновесные ему твердые фазы.

Если коэффициенты, лежащие на одной границе, отличаются более чем несколькими тысячными долями единицы, то все или некоторые составы равновесных твердых фаз, насыщающих нонвариантный раствор, не находятся в вершинах предполагаемых составов твердых фаз. В этом случае находят координаты точек пересечения границ нонвариантных областей друг с другом или с плоскостями и ребрами фигуры состава системы. В полученных точках пересечения вычисляют молярные соотношения всех компонентов, которые представляют собой приблизительные составы равновесных твердых фаз. Округляют полученные соотношения молей компонентов в равновесных составах твердых фаз до ближайших разумных значений, основанных на литературных данных о составах существующих твердых фаз, и проводят триангуляцию исходной системы на подсистемы, опираясь на известные данные о фазовых равновесиях в оконтуривающих системах. В каждой подсистеме пересчитывают все аналитические составы произвольно расположенных реперных точек на всех границах нонвариантных областей на истинные концентрации [Аносов В.Я., Погодин С.А. Основные начала физико-химического анализа. - М.-Л.: Изд-во АН СССР, 1947. - 83 с.] с учетом определенных и округленных молярных составов равновесных твердых фаз или известных составов химических соединений и кристаллогидратов в оконтуривающих системах. Для всех составов на границах нонвариантных областей снова вычисляют коэффициенты, равные отношениям содержаний компонента, который отсутствует в составах равновесных твердых фаз на соответствующих плоскостях или предельных нодах нонвариантной области системы, к содержанию воды.

С целью определения составов нонвариантного раствора в истинной системе координат и подтверждения равновесных ему твердых фаз снова сопоставляют отличия коэффициентов, лежащих на соответствующих границах нонвариантной области, относительно друг друга. Если все отличия не превышают нескольких тысячных долей единицы, вычисляют средние значения коэффициентов на каждой границе и состав нонвариантного раствора, который затем переводят в аналитические концентрации, общепринятые в справочных изданиях.

Вышеперечисленная совокупность существенных признаков позволяет получить следующий технический результат: получение наиболее точных данных о фазовых равновесиях в системе без использования методов химического анализа, исключающих даже гипотетическую возможность появления неизученных фазовых областей, значительное увеличение точности математического прогноза состава нонвариантного раствора, отсутствие потери точности и надежности определения состава нонвариантного раствора при увеличении числа компонентов в системах любого типа, уменьшение трудоемкости процесса экспериментального изучения нонвариантных фазовых равновесий.

Ниже приведены примеры осуществления изобретения.

Пример 1. Определение составов равновесных нонвариантных фаз в пятерной водно-солевой системе простого эвтонического типа с кристаллизацией безводных индивидуальных исходных солевых компонентов без изоляции твердых фаз.

Демонстрацию доказательства отсутствия в системе новой твердой фазы и определения составов равновесных твердых фаз проводим на примере простой пятерной системы эвтонического типа: NH₄H₂PO₄-(NH₄)₂HPO₄-NH₄Cl-(NH₄)₂SO₄-H₂O при 25°C.

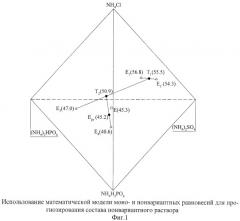
Исходные данные для определения составов нонвариантных равновесных фаз в системе NH₄H₂PO₄-(NH₄)₂HPO₄-NH₄Cl-(NH₄)₂SO₄-H₂O при 25°C и построения математической модели фазовых областей сведены в табл.1 и изображены на фиг.1.

Таблица 1
Исходные данные для прогнозирования состава нонвариантного раствора в системе NH4H2PO4-(NH4)2HPO4-NH4Cl-(NH4)2SO4-H2O при 25°C
Точка	Состав, мас.%	Примечание: Твердая фаза или коэффициент
NH4H2PO4	(NH4)2HPO4	NH4Cl	(NH4)2SO4	H2O
E1	0.00	9.24	10.20	23.73	56.83	(NH4)2HPO4+(NH4)2SO4+NH4Cl
T1	2.99	4.51	13.13	23.85	55.53	0.511475115
E2	5.84	0.00	15.92	23.96	54.28	NH4H2PO4+NH4Cl+(NH4)2SO4
T2	10.73	15.07	12.39	10.93	50.89	0.541762549
E3	17.27	23.99	11.77	0.00	46.97	(NH4)2HPO4+NH4Cl+NH4H2PO4
Epr	14.90	18.57	5.50	15.86	45.17	0.55622569
Е4	18.23	21.37	0.00	19.8	40.6	NH4H2PO4+(NH4)2HPO4+(NH4)2SO4
E	12.83	17.69	7.71	16.44	45.33	NH4H2PO4+(NH4)2HPO4+NH4Cl+(NH4)2SO4

Наиболее простой и адекватной моделью составов жидких фаз моно- и нонвариантных равновесий в системе NH₄H₂PO₄-(NH₄)₂HPO₄-NH₄Cl-(NH₄)₂SO₄-H₂O при 25°C является плоскость, если составы используются в мас.%. Поэтому состав нонвариантного раствора вычисляем по следующей методике.

Расположим составы нонвариантных растворов оконтуривающих четверных систем по убыванию содержания в них воды и последовательно вычислим координаты ряда промежуточных точек по уравнению прямой. Состав первой точки T₁ вычисляем между эвтоническими растворами E₁ и Е₂, с наибольшими содержаниями воды, обратно пропорционально ее количеству в этих растворах. Состав точки Т₂ вычисляем аналогично, по содержанию воды в точках T₁ и Е₃. Предполагаемый нонвариантный раствор E_pr вычисляем между точками Т₂ и Е₄ (табл.1, фиг.1).

Найденный состав предполагаемого эвтонического раствора (E_pr) перспективно проецируем на оконтуривающие четверные системы NH₄ ⁺||Н₂РО₄ ^-, HPO₄ ^2-, Cl^--H₂O, NH₄ ⁺||H₂PO₄ ^- SO₄ ^2-, Cl^--H₂O, NH₄ ⁺||SO₄ ^2-, HPO₄ ^2-, Cl^--H₂O, NH₄ ⁺||H₂PO₄ ^-, HPO₄ ^2-, SO₄ ^2--H₂O. Проекции E_pr находятся в гомогенной области двух оконтуривающих систем: NH₄||H₂PO₄ ^-, HPO₄ ^2-, Cl^--H₂O и NH₄ ⁺||H₂PO₄ ^-, HPO₄ ^2-, SO₄ ^2--Н₂O при 25°C, что позволяет использовать сечения типа «раствор трех солей» - «четвертая соль». Данный тип сечений позволяет определить составы на гранях нонвариантной области (a₁ и b₁ в табл.2), составляя исходные смеси компонентов (ИСК) двумя взвешиваниями, что уменьшает трудоемкость и увеличивает точность получаемых результатов, так как все приготовленные ИСК находятся строго на одной прямой.

Для определения составов фигуративных точек на других гранях нонвариантной области (d₁, d₂, c₁, с₂, f₁, f₂ в табл.2) используем сечения в изогидрическом разрезе, с содержанием воды 40 мас.%.

Все составы ИСК изученных сечений изогидрического разреза готовили взвешиванием раствора двух солей, к которым прибавляли две оставшиеся соли.

Экспериментально по функциональным кривым "состав-свойство" найдены точки излома на границах нонвариантной области, составы которых сведены в табл.2. В них найдены отношения содержаний компонента (основные коэффициенты), который отсутствует в составах равновесных твердых фаз на соответствующих плоскостях нонвариантной области системы, к содержанию воды.

Таблица 2
Исходные данные для прогнозирования состава нонвариантного раствора в системе NH4H2PO4-(NH4)2HPO4-NH4Cl-(NH4)2SO4-H2O при 25°C
Репер ная точка	Состав, мас.%	Грань	Основные коэффициенты
NH4ClA	(NH4)2HPO4 B	NH4H2PO4 C	(NH4)2SO4 D	H2O	{A}/{H2O}	{B}/{H2O}	{C/{H2O}	{C}/{H2O}
d2	9.70	20.02	15.82	14.44	40.03	ABC				0.3606
b1	9.13	18.39	13.90	15.65	42.93	ABC				0.3646
c1	8.83	21.66	11.32	18.20	40.00	ABD			0.2830
f1	9.38	22.77	11.33	16.52	40.00	ABD			0.2833
c2	8.83	15.52	17.45	18.20	40.00	ACD		0.3880
f2	9.38	15.71	18.39	16.52	40.00	ACD		0.3928
a1	6.77	19.67	16.35	17.88	39.33	BCD	0.1721
d1	6.72	19.98	15.78	17.51	40.00	BCD	0.1680
Средние значения коэффициентов	c1=0.1701	c2=0.3904	c3=0.2831	c4=0.3626

Сопоставив отличия коэффициентов, лежащих на одной границе, относительно друг друга, определили, что они отличаются не более чем на 0.005. Таким образом, составы всех точек приведены в истинной системе координат и равновесными твердыми фазами, насыщающими нонвариантный раствор, являются исходные безводные солевые компоненты.

По экспериментальным средним основным коэффициентам вычисляем состав нонвариантного раствора (E, см. табл.1, фиг.1). Состав эвтонического раствора вычисляем по следующим формулам (1-5):

где: c₁={NH₄Cl}/{H₂O}; c₂={(NH₄)₂HPO₄}/{H₂O}; c₃={NH₄H₂PO₄}/{H₂O} с₄={(NH₄)₂SO₄}/{H₂O}; {NH₄Cl}, {(NH₄)₂HPO₄}, {NH₄H₂PO₄} и {(NH₄)₂SO₄} - содержание (мас.%) хлорида, гидрофосфата, дигидрофосфата, сульфата аммония и воды в среднем эвтоническом растворе (E). Экспериментально найденный состав этого раствора хорошо согласуется с предполагаемым составом, вычисленным по математической модели.

Пример 2. Определение составов нонвариантных равновесных фаз в водно-солевой системе Na₂SO₄-Na₂CO₃-NaCl-H₂O с кристаллизацией инконгруэнтно растворимого химического соединения Na₂CO₃·2Na₂SO₄ и образованием кристаллогидрата Na₂C₃·H₂O без изоляции твердых фаз.

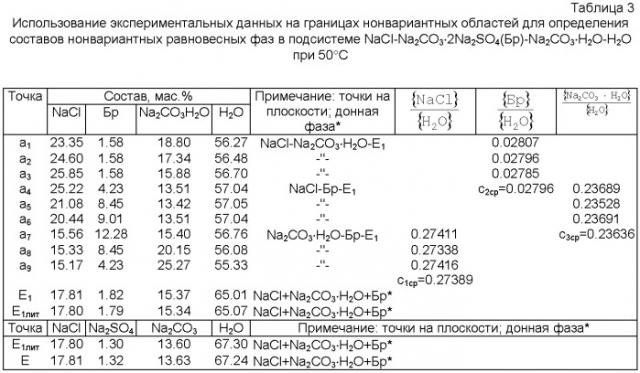
Демонстрацию процедуры определения в четверной системе составов нонвариантных фаз проведем на примере диаграммы состояния Na₂SO₄-Na₂CO₃-NaCl-H₂O при 50°C [Здановский А.Б., Ляховская Е.И., Шлеймович Р.Э. Справочник экспериментальных данных по растворимости многокомпонентных водно-солевых систем. Л.: ГХИ, 1954. - Т.2. - С.694], в которой образуется кристаллогидрат состава Na₂CO₃H₂O - моногидрат карбоната натрия и химическое соединение - беркеит (Бр: Na₂CO₃·2Na₂SO₄) в тройной оконтуривающей системе Na₂SO₄-Na₂CO₃-H₂O при 50°C.

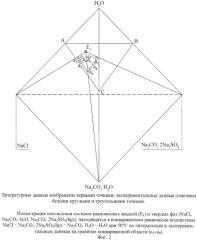
Исходные литературные и экспериментальные данные для определения составов нонвариантных равновесных фаз в системе Na₂SO₄ - Na₂CO₃ - NaCl - H₂O при 50°С сведены в табл.3, 4 и изображены на фиг.2, 3.

Основываясь на данных о фазовых равновесиях в тройной оконтуривающей системе Na₂SO₄-Na₂CO₃-H₂O при 50°С, триангулируем исходную четверную систему на две четверные подсистемы NaCl-Na₂CO₃·2Na₂SO₄(Бp)-Na₂CO₃·H₂O-H₂O и NaCl-Na₂CO₃·2Na₂SO₄(Бр)-Na₂SO₄-H₂O. Для нахождения составов нонвариантных равновесных фаз в каждой подсистеме экспериментально определяем составы ИСК (фиг.2, точки a₁÷a₉, фиг.3, точки b₁÷b₈ соответственно), находящиеся на всех границах нонвариантных областей при помощи сечений изогидрических разрезов (59 мас.% воды). Для чего приготовленные ИСК в исследованных сечениях доводим до равновесия, измеряем показатель преломления жидких фаз, строим функциональные кривые "состав-свойство" и на них находим точки изломов на границах нонвариантных областей, пересчитав их на истинные координаты в каждой соответствующей подсистеме.

Для нахождения составов нонвариантных равновесных фаз в подсистеме NaCl-Na₂CO₃·2Na₂SO₄(Бр)-Na₂CO₃·H₂O-H₂O при 50°C экспериментально определяем составы ИСК (фиг.2, точки a₁÷a₉, табл.3), находящиеся на всех границах нонвариантной области (точки a₁÷a₃ на грани NaCl-Na₂CO₃·H₂O-E₁, на которой в равновесных твердых фазах отсутствует беркеит; точки a₁÷a₆ на грани NaCl-Na₂CO₃·2Na₂SO₄(Бр)-E₁, на которой в равновесных твердых фазах отсутствует моногидрат карбоната натрия; точки a₇÷a₉ на грани Na₂CO₃·H₂O-Na₂CO₃-2Na₂SO₄(Бр)-E₁, на которой в равновесных твердых фазах отсутствует хлорид натрия), при помощи сечений изогидрического разреза (59 мас.% воды). Вычисляем отношения содержаний беркеита к воде в точках a₁÷a₃ (c₂); моногидрата карбоната натрия к воде в точках a₄÷a₆ (с₃); хлорида натрия к воде в точках a₇÷a₉ (c₃), сравнивая значения необходимых коэффициентов, определяем, что отличия в коэффициентах c₂ и c₃ составляют 0.002, а коэффициентов c₁ - 0.001. Следовательно, равновесными твердами фазами, насыщающими нонвариантный раствор E₁, являются моногидрат карбоната натрия, хлорид натрия и беркеит. Далее вычисляем средний состав эвтонического раствора в истинных координатах по формулам:

где: c_{1 ср.}={NaCl}/{H₂O}; c_{2 ср.}={Na₂CO₃·2Na₂SO₄(Бр)}/{H₂O}; с_{3 ср.}={Na₂CO₃·H₂O}/{H₂O}; {NaCl}, (Na₂CO₃·2Na₂SO₄(Бр)}, {Na₂CO₃·H₂O} и {H₂O} - содержание (мас.%) хлорида натрия, беркеита и моногидрата карбоната натрия и воды в среднем составе эвтонического раствора (E₁). Пересчитываем состав эвтонического раствора (E₁) в аналитические координаты. Установленный средний экспериментальный состав эвтонического раствора незначительно отличается от литературных данных.

Для нахождения составов нонвариантных равновесных фаз в подсистеме NaCl-Na₂CO₃·2Na₂SO₄(Бр)-Na₂SO₄-H₂O при 50°C экспериментально определяем составы ИСК (фиг.3, точки b₁÷b₈, табл.4), находящиеся на всех границах нонвариантной области (точки b₁÷b₃ на грани NaCl-Na₂SO₄-Е₂, на которой в равновесных твердых фазах отсутствует беркеит; точки b₄÷b₆ на грани NaCl-Na₂CO₃·2Na₂SO₄(Бр)-Е₂, на которой в равновесных твердых фазах отсутствует сульфат натрия; точки b₇÷b₈ на грани Na₂SO₄-Na₂CO₃·2Na₂SO₄(Бр)-Е₂, на которой в равновесных твердых фазах отсутствует хлорид натрия), при помощи сечений изогидрического разреза (59 мас.% воды). Вычисляем отношения содержаний беркеита к воде в точках b₁÷b₃ (с₅); сульфата натрия к воде в точках b₄÷b₆ (c₆); хлорида натрия к воде в точках b₇÷b₈ (c₄), сравнивая значения необходимых коэффициентов, определяем, что отличия в коэффициентах с₄, с₅ и с₆ составляют допустимую величину тысячных долей. Следовательно, равновесными твердами фазами, насыщающими нонвариантный раствор Е₂, являются сульфат натрия, хлорид натрия и беркеит. Далее вычисляем средний состав эвтонического раствора в истинных координатах по формулам:

где: с_{4 ср.}={NaCl}/{H₂O}; с_{5 ср.}={Na₂CO₃·2Na₂SO₄(Бр)}/{H₂O}; с_{6 ср.}={Na₂SO₄}/{H₂O}; {NaCl}, {Na₂CO₃·2Na₂SO₄(Бр)}, {Na₂SO₄} и {H₂O} - содержание (мас.%) хлорида натрия, беркеита и сульфата натрия и воды в среднем составе эвтонического раствора (Е₂). Пересчитываем состав эвтонического раствора (Е₂) в аналитические координаты. Установленный средний экспериментальный состав эвтонического раствора незначительно отличается от литературных данных.

Данное описание и примеры рассматриваются как материал, иллюстрирующий изобретение, сущность которого и объем патентных притязаний определены в нижеследующей формуле изобретения, совокупностью существенных признаков и их эквивалентами.

Способ определения составов нонвариантных равновесных фаз многокомпонентных водно-солевых систем, включающий прогнозирование состава нонвариантного раствора, экспериментальное определение составов смесей на границах нонвариантной области и нонвариантных жидких фаз оптимальными исходными смесями компонентов, располагающимися строго в определенном порядке, по измерениям физического свойства жидкой фазы после установления равновесия с помощью функциональной зависимости "состав-свойство", отличающийся тем, что для всех экспериментальных точек, произвольно расположенных на всех границах нонвариантной области по средним отношениям содержаний компонента, который отсутствует в составах равновесных твердых фаз на соответствующих плоскостях или предельных нодах нонвариантной области системы, к содержанию воды, вычисляют состав нонвариантной жидкой фазы и определяют равновесные твердые фазы, используя истинные координаты.