Способ получения двумерного радиолокационного изображения объекта при многочастотном импульсном зондировании

Способ получения двумерного радиолокационного изображения объекта при многочастотном импульсном зондировании

Иллюстрации

Показать все

Реферат

Изобретение относится к области исследования радиолокационных характеристик объекта и получения его радиолокационных изображений (РЛИ) при использовании многочастотного импульсного зондирования и синтезирования апертуры антенны.

Методы получения РЛИ объекта основаны на цифровой обработке комплексной огибающей отраженного от него сигнала, измеренного в широкой полосе частот зондирующих импульсов РЛС при различных ракурсах наблюдения объекта.

Комплексная огибающая отраженного от объекта сигнала имеет вид

,

где А - амплитуда отраженного сигнала,

R - расстояние от РЛС до объекта,

λ - длина волны зондирующего сигнала,

φ_о - скачок фазы, возникающий при отражении от объекта,

π=3,1415926535.

Модель исследуемого объекта - совокупность локальных рассеивающих центров (РЦ), у которых эффективная площадь рассеяния (ЭПР) и координаты в связанной с объектом системе отсчета являются постоянными в течение времени измерения отраженного сигнала.

Известен [Патент RU 2372627 С1. МПК: G01S 13/89 (2006.01), 10.11.2009] способ получения двумерного радиолокационного изображения в большом диапазоне изменения величин эффективных площадей рассеивания локальных рассеивающих центров при многочастотном импульсном зондировании, включающий излучение импульсов с изменением несущей частоты от импульса к импульсу с шагом Δf в полосе частот ΔF, прием отраженных сигналов, измерение комплексных огибающих Ф отраженных сигналов и запоминание их в течение времени синтезирования в секторе углов наблюдения Δψ, образование матрицы комплексных огибающих и преобразование ее с помощью быстрого двумерного преобразования Фурье в двумерную матрицу синтезированных откликов, определение величины порога по уровню первых боковых лепестков наиболее интенсивного отклика, сравнение величин откликов с порогом для выделения превышающих порог элементов матрицы, совокупность которых принимают за радиолокационное изображение объектов, отличающийся тем, что измеряют частоту f(t_nm) зондирующих импульсов, момент времени t_nm запоминают, где n - номер шага перестройки частоты, m - номер повторного цикла перестройки, измеряют в земной системе отсчета в момент времени t_nm координаты центра антенны радиолокационной станции (РЛС) и выбранного центра синтезирования на объекте, измеряют относительно земной системы отсчета угол наблюдения ψ(t_nm) связанной с объектом системы отсчета с началом в центре синтезирования, вычисляют пространственные частоты

где с - скорость света, ψ₀ - угол между линией, соединяющей фазовый центр антенны РЛС с центром синтезирования, и осью z земной системы отсчета, фазы измеренных комплексных огибающих отраженных сигналов корректируют к расстоянию от центра антенны РЛС до точки синтезирования, полученные после коррекции значения комплексных огибающих размещают в элементы двумерной матрицы с номерами (k, l), где

int[^*] - функция определения целой части числа, d - шаг изменения значений пространственных частот, матрицу подвергают двумерному дискретному преобразованию Фурье и по полученной матрице синтезированных откликов в координатах (х, z) связанной с объектом системы отсчета определяют оценки координат и ЭПР РЦ с большими значениями ЭПР, затем уточняют эти оценки по минимуму функции энергии матрицы комплексных огибающих, корректируют исходную матрицу комплексных огибающих путем изъятия информации о РЦ с большими значениями ЭПР и повторно синтезируют матрицу откликов, получая РЛИ с РЦ, имеющими малые значения ЭПР.

Основным достоинством указанного способа синтезирования двумерных РЛИ, в отличие от использовавшихся ранее ([Патент RU 2099743 С1. МПК: G01S 13/89, 20.12.1997], [Нестеров С.М. и др. Особенности формирования двумерных радиолокационных изображений объектов ступенчатыми ЛЧМ сигналами. «Радиотехника», 2001, №5]), является обеспечение повышения разрешающей способности РЛИ и точности оценок РЦ при расширении сектора углов поворота объекта относительно линии визирования, что достигается за счет формирования матрицы комплексных огибающих в координатах пространственных частот. Поскольку значения пространственных частот и координат РЦ в записи фазы комплексных огибающих связаны линейным образом, то в результате преобразования Фурье отраженный сигнал, определенный в области пространственных частот, преобразуется в область декартовых координат без искажения при увеличении полосы частот и сектора углов поворота.

Описанный способ взят в качестве прототипа.

Недостатком указанного способа является нереализуемость заложенной в измеренной информации потенциальной точности разрешения РЦ. Так, по результатам моделирования [Патент RU 2372627 С1. МПК: G01S 13/89 (2006.01), 10.11.2009] в первично синтезированном РЛИ с вероятностью, близкой к 1, разрешаются РЦ объекта в диапазоне изменения ЭПР не более 12 дБ. Расширение этого диапазона достигается использованием дополнительной математической обработки первичного РЛИ, заключающейся в уточнении оценок РЦ с большими значениями ЭПР, и повторном синтезировании РЛИ по матрице комплексных огибающих с изъятой информацией о РЦ с большими ЭПР. В результате удается расширить диапазон ЭПР разрешаемых РЦ до 20 дБ. Дальнейшее расширение этого диапазона способом-прототипом проблематично.

Подобный результат объясняется тем, что в прототипе не обеспечивается формирование двумерных РЛИ с достижимой для заданной полосы частот разрешающей способностью. При формировании РЛИ в прототипе задается как полоса частот, так и размер интервала углов синтезирования. То есть не учитывают, что заданная полоса частот определяет размер сектора углов, для которого реализуется достижимая разрешающая способность двумерного РЛИ, и что синтезирование такого РЛИ обеспечивается при условии выявления требуемых пределов изменения и значений пространственных частот, которые зависят от заданной полосы частот, связанного с ней размера сектора углов наблюдения, а также заданных размеров области синтезирования РЛИ.

В способе-прототипе задают полосу частот и интервал изменения углов, по измеренным углам и частотам рассчитывают возможные значения пространственных частот, по которым получают номера матрицы комплексных огибающих, используя шаг d изменения значений пространственных частот, задаваемый произвольным образом. После чего в элементы матрицы с вычисленными таким образом номерами заносят измеренные значения комплексных огибающих.

При подобном формировании матрицы комплексных огибающих в один и тот же элемент матрицы могут заноситься разные измеренные значения, в результате чего не вся измеренная и значимая информация будет использована при построении РЛИ. Поэтому, при попытке записи нового измеренного значения в уже заполненный элемент матрицы, в прототипе уменьшают шаг d и пропорционально увеличивают тем самым размер матрицы. На практике это приводит к формированию матрицы комплексных огибающих, размеры которой в несколько раз больше необходимых, причем некоторые элементы этой большой матрицы оказываются незаполненными, что, с одной стороны, ухудшает качество получаемых РЛИ, а с другой, из-за увеличения объема вычислений, ограничивает возможность реализации режима формирования РЛИ в реальном масштабе времени.

Для формирования матрицы комплексных огибающих, обеспечивающей достижимую для заданной полосы частот разрешающую способность синтезируемых РЛИ, предлагается решать обратную задачу: получив значения пространственных частот, вычислить по ним соответствующие значения частоты и угла, а затем выбрать из измеренных соответствующие им значения комплексных огибающих. При этом требуется вычислить требуемые размер интервала углов наблюдения и диапазон изменения пространственных частот (в этой связи необходимо отметить ошибку авторов, полагающих, что диапазон изменения координат f_x, f_z равен , где f_max - максимальное значение частоты в полосе ее перестройки. Очевидно, что такой диапазон изменения f_x, f_z соответствует полосе частот с максимальным значением частоты, равным , и минимальным, равным 0).

В результате перечисленных недостатков прототипа падает разрешающая способность формируемого РЛИ, изображение расфокусируется, и в целом способ не обеспечивает достижения потенциальной точности разрешения РЦ.

Предлагается способ, позволяющий избежать указанных недостатков.

Способ решает задачу получения двумерного РЛИ объекта с достижимой для заданной полосы частот разрешающей способностью, обеспечивая повышение точности определения координат и ЭПР РЦ в широком диапазоне изменения их ЭПР.

Технический результат, заключающийся в повышении точности определения координат и ЭПР РЦ в широком диапазоне изменения их ЭПР в соответствии с достижимой для заданной полосы частот зондирующего сигнала разрешающей способностью РЛИ, достигается путем вычисления размера Δψ половины сектора углов наблюдения, запоминания измеренных комплексных огибающих отраженных сигналов в секторе углов ±Δψ, вычисления по заданной полосе частот и полученному размеру сектора углов наблюдения пределов изменения пространственных частот и их значений, образования двумерной матрицы комплексных огибающих путем выбора из измеренных тех значений, которые соответствуют результатам вышеуказанных вычислений, что в целом позволяет синтезировать РЛИ объекта с достижимой для заданной полосы частот разрешающей способностью и обеспечивает разрешение РЦ объекта в более широком, по сравнению с прототипом, диапазоне изменения их ЭПР даже без используемой в прототипе дополнительной математической обработки.

Для достижения указанного технического результата в известном способе получения двумерного радиолокационного изображения объекта при многочастотном импульсном зондировании, включающем излучение импульсов с изменением несущей частоты f от импульса к импульсу с шагом Δf в полосе частот ΔF, измерение частоты f(t_nm) зондирующих импульсов в моменты времени t_nm, где n - номер шага перестройки частоты, m - номер повторного цикла перестройки, измерение в земной системе отсчета в те же моменты времени координат центра антенны радиолокационной станции (РЛС) и координат выбранного центра синтезирования на объекте, измерение относительно земной системы отсчета угла наблюдения ψ(t_nm) связанной с объектом системы отсчета с началом в центре синтезирования, прием отраженных сигналов, измерение комплексных огибающих Ф(t_nm) отраженных сигналов, корректировку фазы измеренных комплексных огибающих отраженных сигналов по расстоянию от центра антенны РЛС до точки синтезирования, запоминание измеренных комплексных огибающих отраженных сигналов в течение времени синтезирования в угловом секторе, образование двумерной матрицы комплексных огибающих в координатах пространственных частот , и преобразование ее с помощью быстрого двумерного преобразования Фурье в двумерную матрицу синтезированных откликов, определение величины порога по уровню первых боковых лепестков наиболее интенсивного отклика, сравнение величин откликов с порогом для выделения превышающих порог элементов матрицы, определение радиолокационного изображения объектов в виде совокупности выделенных элементов матрицы, согласно изобретению

определяют размер Δψ половины сектора углов наблюдения, исходя из соотношения

где , f_cp - средняя частота в полосе перестройки, запоминают измеренные комплексные огибающие отраженных сигналов в секторе углов наблюдения ±Δψ, заносят в элементы с номерами (n₁, m₁) двумерной матрицы комплексных огибающих значения, полученные для номера n₂ шага перестройки частоты и номера m₂ повторного цикла перестройки, где , , с - скорость света, n₁=1,…,N₁, m₁=1,…,M₁, N₁=L_z(max f_z - min f_z), M₁=L_x(max f_x - min f_x), L_z, L_x - размеры области синтезирования радиолокационного изображения по продольной z и поперечной х координатам, , , , , , , , .

Из приведенной совокупности существенных признаков предлагаемого способа следует, что общими с прототипом являются признаки излучения зондирующих импульсов с изменением несущей частоты от импульса к импульсу в полосе частот ΔF, измерения частоты зондирующих импульсов, измерения в земной системе отсчета координат центра антенны радиолокационной станции (РЛС) и координат выбранного центра синтезирования на объекте, измерения относительно земной системы отсчета угла наблюдения ψ связанной с объектом системы отсчета с началом в центре синтезирования, приема отраженных сигналов, измерения комплексных огибающих отраженных сигналов, корректировки фазы измеренных комплексных огибающих отраженных сигналов к расстоянию от центра антенны РЛС до точки синтезирования, запоминания измеренных комплексных огибающих отраженных сигналов в течение времени синтезирования в угловом секторе, образования двумерной матрицы комплексных огибающих и преобразования двумерной матрицы комплексных огибающих с помощью быстрого двумерного преобразования Фурье в двумерную матрицу синтезированных откликов, определения величины порога по уровню первых боковых лепестков наиболее интенсивного отклика, сравнения величин откликов с порогом для выделения превышающих порог элементов матрицы, определения радиолокационного изображения в виде совокупности выделенных элементов матрицы и вычисления для них оценок координат и ЭПР РЦ.

Признаки запоминания комплексных огибающих в угловом секторе и образования матрицы комплексных огибающих являются общими с прототипом только формально, так как определены размеры матрицы комплексных огибающих и предложено правило выбора измеренных значений комплексных огибающих в качестве элементов этой матрицы.

Признак определения размера Δψ половины сектора углов наблюдения, в котором для обеспечения достигаемой для заданной полосы частот разрешающей способности РЛИ необходимо запоминать измеренные комплексные огибающие, является отличительным.

Описание предлагаемого способа заключается в следующем.

Известно [Патент RU 2372627 С1. МПК: G01S 13/89 (2006.01), 10.11.2009], что оператор синтезирования РЛИ после свертки комплексных огибающих с фокусирующей опорной функцией и с учетом условий дальней зоны локации представляется в виде

где g, z, x - неизвестные параметры РЦ: амплитуда отраженного ими сигнала и их декартовы координаты в продольном (по дальности) и поперечном направлениях в плоскости локации, связанной с объектом системы отсчета;

Ф^*(f_z, f_x) - значения в области переменных f_z и f_x измеренных комплексных огибающих Ф(t_nm), фазы которых скорректированы для обеспечения постоянной дальности от центра антенны РЛС до центра синтезирования РЛИ в течение времени синтезирования,

В (3), в отличие от (1), но не ограничивая общности рассуждения, для удобства выкладок предполагается, что ракурс синтезируемого РЛИ ψ₀=0 (т.е. ось z земной системы выбирается в направлении линии, соединяющей фазовый центр антенны РЛС с центром синтезирования), угол наблюдения ψ отсчитывается в противоположном направлении и изменен порядок интегрирования. С учетом этого замечания преобразование (2) точно повторяет (17) из [Патент RU 2372627 С1. МПК: G01S 13/89 (2006.01), 10.11.2009].

Дискретную форму преобразования (2) запишем в виде

где

L_z, L_x - задаваемые размеры области синтезирования РЛИ по продольной z и поперечной х координатам.

Нелинейная зависимость координат f_z, f_x от угла ψ приводит к сложной взаимосвязи пределов изменения их значений с размерами полосы перестройки частоты и сектора угла наблюдения.

В предлагаемом способе вычисляют требуемые для заданной полосы перестройки частоты размер сектора углов наблюдения и пределы изменения введенных пространственных частот, реализующие достижимую разрешающую способность РЛИ.

Из (4)следует, что

где f_max, f_min - максимальное и минимальное значения частоты в полосе ΔF.

В силу симметрии задачи достижимая разрешающая способность двумерных РЛИ Δ₂ обеспечивается при условии равенства разрешающих способностей по координатам z и х:

где , .

Решая (6)-(10), последовательно получаем

,

где ,

, f_cp - средняя частота в полосе перестройки,

- средняя в полосе перестройки длина волны.

Сравнивая (11) и (16), получаем удобную для практики оценку разрешающей способности двумерных РЛИ: Δ₂≈Δ₁, где (при увеличении Δψ от 0 до 90° относительное превышение Δ₂ над Δ₁ монотонно увеличивается от 0 до, примерно, 12%; так что при Δψ=90°, то есть близкой к 200% перестройке частоты, Δ₂≈1,12Δ₁, где ).

В соответствии с полученными из (11)-(15) размером интервала углов наблюдения и пределами изменения пространственных частот вычисляют размеры матрицы комплексных огибающих, шаг изменения значений пространственных частот, значения пространственных частот, относительно которых необходимо формировать матрицу комплексных огибающих, а затем соответствующие им значения частоты f и угла наблюдения ψ, для которых требуется измерить (или получить из уже измеренных) значения комплексных огибающих.

При синтезировании РЛИ объекта в предлагаемом способе используют следующую последовательность действий.

Задают ракурс синтезируемого РЛИ ψ₀.

Из (11) определяют размер половины сектора углов наблюдения Δψ.

В интервале углов наблюдения ψ₀±Δψ измеряют и запоминают моменты времени t_nm, где n - номер шага перестройки частоты, m - номер повторного цикла перестройки, частоты f(t_nm) зондирующих импульсов, углы наблюдения ψ(t_nm) связанной с объектом системы отсчета, комплексные огибающие отраженных от объекта сигналов Ф(t_nm) и координаты в земной системе отсчета центра антенны РЛС и центра связанной с объектом системы отсчета.

Из (12)-(15) находят значения min f_z, max f_z, min f_x, max f_x.

Из (5) вычисляют значения N₁, М₁.

Вычисляют расстояния между центром антенны и центром связанной системы отсчета в моменты измерений и по ним корректируют фазы измеренных комплексных огибающих.

Измеренные углы наблюдения корректируют по ракурсу ψ₀.

Вычисляют значения частот , где n=1,…,N; N - количество шагов перестройки частоты; min f - минимальное значение частоты в заданной полосе ее перестройки.

Вычисляют значения пространственных частот:

, , n₁=1,…N₁;

, , m₁=1,…M₁.

Формируют матрицу T(n₁, m₁), в элементы которой с номерами (n₁, m₁) заносят значения комплексных огибающих , где номера n₂, m₂ выбирают последовательно из условии , .

С целью снижения уровня боковых лепестков от синтезируемых откликов РЦ используют весовую обработку матрицы в соответствии с цифровым фильтром (окном) Хэмминга, для чего корректируют элементы матрицы Т(n₁, m₁), исходя из соотношения [Хэмминг Р.В. Цифровые фильтры. М.: «Сов. радио». 1980. С.100]

.

Увеличивают размерность матрицы T^* до К=2^P, где р - целое число, путем добавления нулевых элементов с номерами (n₁, m₁), где

N₁<n₁≤К, M₁<m₁≤К.

Затем матрицу Т^* подвергают двумерному быстрому дискретному преобразованию Фурье и по полученной двумерной матрице синтезированных откликов определяют двумерное радиолокационное изображение объекта как совокупность откликов, интенсивность которых превышает задаваемый порог по величине ЭПР от значения наиболее интенсивного отклика.

В условиях нулевых ошибок измерений этот порог определяется параметрами использованной весовой функции (цифрового фильтра). Известно [Хэмминг Р.В. Цифровые фильтры. М.: «Сов. радио». 1980], что применение функции Хэмминга приводит к снижению уровня боковых лепестков отклика от РЦ на -43 дБ и расширению отклика в 2 раза.

На практике, с учетом существующих погрешностей измерений и нестабильности работы измерительной аппаратуры, значение порога уменьшают в соответствии с критерием выявления образа объекта на фоне шума.

Работоспособность предлагаемого способа проверена методом математического моделирования.

Условия локации при моделировании заданы как в известном способе [Патент RU 2372627 С1. МПК: G01S 13/89 (2006.01), 10.11.2009]:

зондирующие сигналы РЛС - импульсы с периодом повторения 20 мкс,

несущая частота сигнала меняется от импульса к импульсу с шагом 3000/511 МГц в полосе частот от 8500 до 11500 МГц,

объект равномерно вращается со скоростью 12°/c.

Модель объекта задана в виде совокупности неподвижных относительно связанной системы отсчета РЦ, которые расположены тремя изолированными группами по 9 РЦ в каждой группе с удалением соседних РЦ по одной из координат на 40 см.

Диапазон значений ЭПР заданных РЦ выбран равным 40 дБ.

ЭПР каждой тройки РЦ, расположенных в линию, задавалась одинаковой.

Заданные значения ЭПР РЦ соседних троек отличаются с шагом -5 дБ, так что ЭПР РЦ в первой тройке равна 0 дБ, во второй -5 дБ, в третьей -10 дБ, в последней девятой -40 дБ.

Из (11) и (16) следует, что для заданной 30% перестройки частоты размер половины сектора углов синтезирования составляет примерно 10° (заметим, что при моделировании в прототипе задавался неоптимальный размер сектора углов, равный 16°), а достижимая разрешающая способность РЛИ равна Δ₂≈1,7 λ_ср, (или 3,4 λ_ср при использовании весовой обработки).

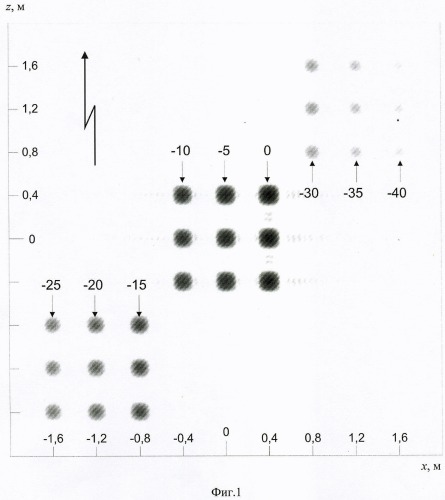
На фиг.1 приведено двумерное РЛИ объекта в плоскости локации, полученное предложенным способом в секторе углов наблюдения ±10° относительно ракурса синтезированного РЛИ без учета ошибок измерения амплитуды и фазы комплексных огибающих, а также координат центра синтезирования и углов курса.

Использовано весовое окно Хэмминга. Порог отрисовки РЛИ по величине ЭПР задан равным -45 дБ.

Различная интенсивность элементов матрицы синтезированных откликов показана на фиг.1 разными цветами серой палитры: от белого цвета при значениях ЭПР, равных -45 дБ и меньше, до черного при 0 дБ. На фигуре подписаны заданные значения ЭПР соответствующих троек РЦ.

Анализ полученных результатов показывает, что в условиях отсутствия ошибок измерений предложенный способ обеспечивает разрешение РЦ в диапазоне изменения ЭПР не менее 40 дБ с погрешностью оценок их координат и ЭПР, равной, соответственно,

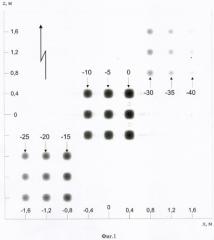
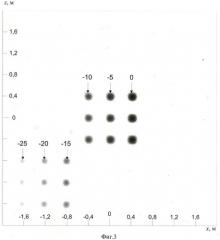
На фиг.2 и 3 приведено двумерное РЛИ объекта в плоскости локации, полученное предложенным способом в том же секторе углов наблюдения с учетом заданных ошибок измерения амплитуды и фазы комплексных огибающих, координат центра синтезирования и углов курса. Значения заданных ошибок соответствуют использованным в прототипе: , δφ=30°, δ_х=δ_z=2 мм, δψ=0,05°.

На фиг.2 порог отрисовки полученного РЛИ по величине ЭПР задан равным -45 дБ, видно большое количество синтезированных ложных откликов в диапазоне изменения значений ЭПР от -30 до -45 дБ. На фиг.3 порог задан равным -30 дБ.

Анализ результатов моделирования показывает, что в условиях заданных ошибок использование предложенного способа обеспечивает разрешение РЦ в диапазоне изменения их ЭПР не менее 25 дБ с вышеуказанной погрешностью оценок координат и значений ЭПР РЦ даже без дополнительной математической обработки матриц комплексных огибающих и синтезируемых откликов, используемой в известном способе. В диапазоне изменения ЭПР более 25 дБ появляются ложные отклики и при уменьшении ЭПР РЦ от -25 дБ до -30 дБ вероятность их идентификации снижается от 1 до 0. При использовании предложенной в способе-прототипе дополнительной математической обработки диапазон разрешаемых РЦ по величине ЭПР увеличивается до 30 дБ.

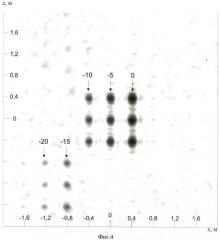
На фиг.4 приведено двумерное РЛИ объекта в плоскости локации, полученное в соответствии со способом-прототипом для тех же условий локации, но в секторе углов наблюдения размером 16° (±8°), как в прототипе. Порог отрисовки синтезированного РЛИ задан как для фиг.3.

Анализ полученного РЛИ показывает, что способ-прототип обеспечивает разрешение РЦ с вышеуказанной погрешностью оценок их координат и ЭПР в диапазоне изменения ЭПР не более 20 дБ. В диапазоне изменения ЭПР более 20 дБ синтезируется большое количество ложных откликов, в результате чего вероятность идентификации РЦ с ЭПР менее -20 дБ стремится к 0.

Кроме того, видна расфокусировка РЛИ объекта на фиг.4 по сравнению с фиг.3, что связано с вышеотмеченными недостатками прототипа.

Технический результат достигнут: устранены недостатки прототипа, расширен диапазон по величине ЭПР выделяемых РЦ, обеспечена точность определения их координат и ЭПР в соответствии с разрешающей способностью, достигаемой для заданной полосы частот зондирующего сигнала.

Способ получения двумерного радиолокационного изображения объекта при многочастотном импульсном зондировании, включающий излучение импульсов с изменением несущей частоты f от импульса к импульсу с шагом Δf в полосе частот ΔF, измерение частоты f(t_nm) зондирующих импульсов в моменты времени t_nm, где n - номер шага перестройки частоты, m - номер повторного цикла перестройки, измерение в земной системе отсчета в моменты времени t_nm координат центра антенны радиолокационной станции (РЛС) и координат выбранного центра синтезирования на объекте, измерение относительно земной системы отсчета угла наблюдения ψ(t_nm), связанной с объектом системы отсчета с началом в центре синтезирования, прием отраженных сигналов, измерение комплексных огибающих Ф(t_nm) отраженных сигналов, корректировку фазы измеренных комплексных огибающих отраженных сигналов к расстоянию от центра антенны РЛС до точки синтезирования, запоминание измеренных комплексных огибающих отраженных сигналов в течение времени синтезирования в угловом секторе, образование двумерной матрицы комплексных огибающих в координатах пространственных частот , и преобразование ее с помощью быстрого двумерного преобразования Фурье в двумерную матрицу синтезированных откликов, определение величины порога по уровню первых боковых лепестков наиболее интенсивного отклика, сравнение величин откликов с порогом для выделения превышающих порог элементов матрицы, определение радиолокационного изображения объектов в виде совокупности выделенных элементов матрицы, отличающийся тем, что определяют размер половины сектора углов наблюдения Δψ, исходя из соотношения где , f_cp - средняя частота в полосе перестройки, запоминают измеренные комплексные огибающие отраженных сигналов в секторе углов наблюдения ±Δψ, заносят в элементы с номерами (n₁, m₁) двумерной матрицы комплексных огибающих значения, полученные для номера n₂ шага перестройки частоты и номера m₂ повторного цикла перестройки, где , , , с - скорость света,n₁=1,…N₁, m₁=1,…M₁, N₁=L_z(max f_z - min f_z), M₁=L_x(max f_x - min f_x),L_z, L_x - размеры области синтезирования радиолокационного изображения по продольной z и поперечной х координатам, , , , , , , , .