Способ триангуляции целей

Способ триангуляции целей

Иллюстрации

Показать все

Реферат

Область техники

Данное техническое решение относится к области радиолокации и вычислительной техники, а именно к определению местоположения объекта путем сопоставления в одной системе координат двух и более найденных направлений на объект.

Уровень техники

Требования к возможностям методов триангуляции для определения координат объектов возрастают для применения в области разведки излучающих воздушных объектов. Повышаются требования к точности определения координат. Количество объектов может быть большим. Использование активных средств локации (облучение объекта) допускается только кратковременное. Не должно быть ограничений на дислокацию и перемещения пеленгаторов.

Известные методы триангуляции (Л1), определяющие координаты объекта на плоскости XY или пространственные координаты объекта, используют допущение о наличии точки пересечения пеленгов на плоскости или в пространстве. Для триангуляционной системы, состоящей из двух пеленгаторов, такое допущение означает, что оба пеленга и база пеленгаторов должны лежать в одной плоскости. Для определения координат цели на плоскости ХУ по однокоординатным пеленгаторам (только азимут) такое допущение приемлемо. С появлением двухкоординатных пеленгаторов (азимут и угол места) и определением трех пространственных координат цели такое допущение приводит к усложнению решения задачи. В (Л1) приводится алгоритм определения трех пространственных координат цели по информации четырех двухкоординатных пеленгаторов. Эти пеленгаторы должны размещаться определенным образом, что практически исключает возможность работы в движении. Кроме того, для решения задачи размножения целей нужна дополнительная информация, получение которой требует облучения объекта.

Аналогом заявляемого способа триангуляции целей является Способ формирования маршрута носителя пеленгатора, определяющего местоположение излучателя методом триангуляции (патент на изобретение RU 2303794 C2, заявка 2005126126 от 17.08.2006, МПК G01S 5/02, опубликован 27.02.2007).

Достоинством способа для рассматриваемой области применения является необходимость только одного пеленгатора и пассивные средства определения местоположения излучателя. Однако излучатель должен быть только неподвижным, координаты определяются на плоскости, пеленгатор должен перемещаться по определенному маршруту. Для рассматриваемой области применения способ не приемлем.

Другими аналогами можно назвать Способ бесконтактного измерения толщины объекта (патент на изобретение SU 1826697 А1, заявка 4829581 от 25.05.1990, МПК G01B 11/06, опубликован 10.06.1996) и Способ бесконтактного измерения толщины (патент на изобретение SU 1826698 А1, заявка 4844737 от 25.05.1990, МПК G01B 11/06, опубликован 10.06.1996).

Способ бесконтактного измерения толщины объекта для случая определения координат подвижных целей не приемлем, так как требует активного облучения контролируемого объекта и определенной взаимной ориентации источников облучения и приемников световых пятен.

Наиболее близким аналогом (прототипом) заявляемого способа триангуляции целей является Способ создания космической геодезической сети (патент на изобретение RU №2337372 C2, заявка 2006101927 от 27.07.2007, МПК G01S 5/00, опубликован 27.10.2008), включающий дальномерные, доплеровские и фотографические измерения с пунктов космической геодезической сети на геодезический спутник и уравнивание этих измерений динамическим методом космической геодезии с разбиением совокупности всех измерений на группу измерений, равномерно распределенных на длинных орбитальных дугах для отнесения начала координат космический геодезической сети к центру масс Земли, и на группу измерений, отнесенных на короткие орбитальные дуги для уточнения взаимного положения пунктов космической геодезической сети, с включением в короткие дуги в качестве неизвестных элементов взаимного трансформирования решений по длинным и коротким дугам, при этом выполняют дополнительные дальномерные измерения между геодезическим спутником и спутниками космической навигационной системы для заполнения разрывов в совокупности измерений на длинных орбитальных дугах и дальномерные измерения с части пунктов космической геодезической сети до спутников космической навигационной системы, отличающийся тем, что используют второй геодезический космический аппарат, разнесенный по орбите от первого геодезического космического аппарата на некоторое линейное расстояние, и методом космической триангуляции определяют координаты подвижного космического объекта, для чего указанными выше дальномерными, доплеровскими и фотографическими измерениями уточняют базис между геодезическими космическими аппаратами, осуществляют привязку подвижного космического объекта к каталожным звездам, координаты которых точно определены в абсолютной системе координат, а углы между базисом и направлениями «геодезический космический аппарат - космический объект» измеряют бортовой оптико-электронной аппаратурой, установленной на борту каждого геодезического космического аппарата, по измеренным значениям базиса и двух углов определяют стороны измерительного треугольника, в вершинах которого в момент измерений находятся два геодезических космических аппарата и космический объект соответственно, и тем самым измеряют дальности между геодезическими космическими аппаратами и космическим объектом, по которым определяют радиус-вектор космического объекта в инерциальной системе координат в момент проведения измерений, дифференцируют по времени координаты космического объекта, полученные в серии измерений с заданным шагом, определяя тем самым вектор скорости космического объекта на заданный момент времени, по измеренным значениям радиус-вектора и вектора скорости космического объекта на заданный момент времени определяют параметры орбиты космического объекта.

Достоинством прототипа является возможность определения, кроме местоположения объекта, еще скорости и орбиты перемещения объекта.

Однако недостатком предлагаемого прототипа является то, что способ ориентирован на определение параметров космического объекта, требует для реализации использования космической геодезической сети, спутников навигационной системы, координат каталожных звезд, что затрудняет использование способа для определения координат воздушных целей у поверхности земли.

Сущность изобретения

Известен способ триангуляции целей, реализуемый с помощью двух двухкоординатных пеленгаторов с координатами P1 (x₁, у₁, h₁) и Р2 (х₂, у₂, h₂) точек стояния пеленгаторов, определяющих B₁, E₁ и В₂, Е₂ - азимут и угол места пеленга p₁ и р₂ и использующих эти данные для обработки с помощью средств вычислительной техники.

Целью создания предлагаемого изобретения является решение актуальной задачи определения пространственных координат излучающих воздушных объектов с использованием в основном пассивных средств локации.

В рассматриваемом методе по координатам точек размещения двух пеленгаторов и направлений двух пеленгов на объект определяются координаты точки сближения пеленгов, находящейся между двумя пеленгами на ближайшем расстоянии от пеленгов, и определяется расстояние между пеленгами в точке сближения.

Задача решается использованием нижеприведенного алгоритма обработки входных данных:

P1(x₁, у₁, h₁) точка стояния пеленгатора P1;

Р2(х₂, у₂, h₂) точка стояния пеленгатора Р2;

B₁, E₁ азимут и угол места пеленга р₁;

В₂, Е₂ азимут и угол места пеленга р₂;

шаг 1 - определяются направляющие косинусы cosa_x, cosa_y, cosa_h линии пеленга p₁ и направляющие косинусы cosb_x, cosb_y, cosb_h линии пеленга р₂:

для пеленга p₁:

cosa_x=cos(E₁)cos(B₁);

cosa_y=cos(E₁)sin(B₁);

cosa_h=sin(E₁);

для пеленга р₂:

cosb_x=cos(E₂)cos(B₂);

cosb_y=cos(E₂)sin(B₂);

cosb_h=sin(E₂);

шаг 2 - определяется расстояние t₁ от точки стояния пеленгатора Р1 до точки P_t1 на линии пеленга p₁, для которой расстояние до линии пеленга р₂ минимальное:

,

где a₁=cosa_hcosb_x-cosa_xcosb_h;

а₂=cosa_ycosb_h-cosa_hcosb_y;

а₃=cosa_xcosb_y-cosa_ycosb_x;

b₁=cosa_x(h₂-h₁)-cosa_h(x₂-x₁);

b₂=cosa_h(y₂-у₁)-cosa_y(h₂-h₁);

b₃=cosa_y(x₂-x₁)-cosa_x(у₂-у₁);

шаг 3 - определяется расстояние t₂ от точки стояния пеленгатора Р2 до точки P_t2 на линии пеленга р₂, для которой расстояние до линии пеленга p₁ минимальное:

,

где a₁=cosb_hcosa_x-cosb_xcosa_h;

а₂=cosb_ycosa_h-cosb_hcosa_y;

а₃=cosb_xcosa_y-cosb_ycosa_x;

b₁=cosb_x(h₂-h₁)-cosb_h(x₂-x₁);

b₂=cosb_h(y₂-у₁)-cosb_y(h₂-h₁);

b₃=cosb_y(x₂-x₁)-cosb_x(у₂-у₁);

шаг 4 - определяются координаты точки P_t1 и точки P_t2:

координаты точки P_t1:

x_t1=x₁+t₁·cosa_x;

y_t1=у₁+t₁·cosa_y;

h_t1=h₁+t₁·cosa_h;

координаты точки P_t2:

x_t2=x₂+t₂·cosb_x;

y_t2=у₂+t₂·cosb_y;

h_t2=h₂+t₂·cosb_h;

шаг 5 - вычисляется значение признака С_Р совместимости пеленгов p₁ и р₂:

расстояние между точками P_t1 и P_t2:

d=[(x_t1-x_t2)²+(y_t1-y_t2)²+(h_t1-h_t2)²]^1/2;

максимальное возможное расстояние между пеленгами p₁ и р₂:

d_r=δ_φ·t₁+δ_φ·t₂,

где δ_φ - максимальное угловое отклонение пеленгов от точки цели, определенное для пеленгаторов для максимальных ошибок пеленгации;

если значения t₁ и t₂ положительные и если значение d меньше d_r, то значение признака С_Р устанавливается 1, иначе 0;

при нулевом значении признака С_Р пеленги несовместимы, определение координат точки P_S (шаг 6) не выполняется;

шаг 6 - определяются выходные данные - координаты точки P_S на отрезке P_t1P_t2, для которой расстояние до линии пеленга p₁ и до линии пеленга р₂ минимальное:

x_s=(x_t1·t₁+x_t2·t₂)/(t₁+t₂);

y_s=(y_t1·t₁+y_t2·t₂)/(t₁+t₂);

h_s=(h_t1·t₁+h_t2·t₂)/(t₁+t₂).

Метод позволяет определить три пространственные координаты объекта по двум пеленгам, уменьшить количество ложных целей, обеспечивает возможность определения координат объекта на стоянке носителей пеленгаторов и в движении, позволяет уменьшить время активной локации объекта и получить уточненные координаты цели при количестве пеленгов больше двух.

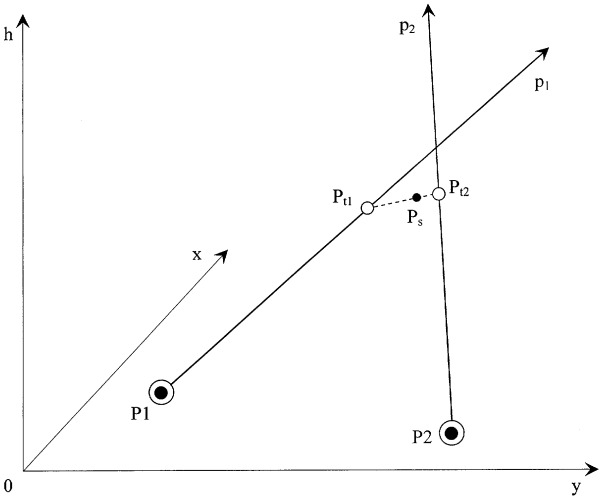
На чертеже изображена диаграмма размещения пеленгаторов и целей.

Пример варианта реализации заявляемого способа

Метод предназначен для использования в решении задачи отождествления целей и задачи постановки целей на сопровождение. Ниже рассматривается метод определения трех пространственных координат объекта разведки по информации двухкоординатных пеленгаторов, независимо измеряющих азимут и угол места объекта.

По двум и более пеленгам цели требуется определить координаты цели. Пеленг цели задается точкой стояния источника пеленга и направлением на цель из точки стояния. Точка стояния определяется координатами (х, у, h), направление на цель задается азимутом (В) и углом места (Е). Параметры задаются в левой прямоугольной системе координат.

Вычисление координат цели по двум пеленгам.

Имеем два пеленга цели р₀ и p₁:

где

r₀, r₁ - векторы точек стояния источников пеленгов;

а₀, a₁ - направляющие векторы прямых р₀, p₁;

t - параметр.

Произвольно выберем один из этих пеленгов, пусть р₀, как «опорный», тогда другой пеленг p₁ будем считать «парным» к опорному. При изменении параметра t от нуля в положительную сторону точка на опорной линии будет перемещаться от точки стояния (x₀ у₀ h₀) в направлении, задаваемом направляющим вектором а₀. Расстояние от этой движущейся точки до прямой p₁, то есть длина перпендикуляра, опущенного из этой точки на парную прямую, определяется выражением (Л2):

Если оба пеленга относятся к одной цели, то в окрестности цели значение d должно быть минимальным. Параметр t, при котором d достигает минимального значения, можно определить, продифференцировав выражение (2) по t. Если задать для перемещения точки на линии опорного пеленга единичную скорость, то численно полученная величина t будет равна длине отрезка от начальной точки до той точки, для которой d минимально.

Повторив аналогичные вычисления, считая теперь пеленг p₁ опорным, а пеленг р₀ парным, получим точку на линии p₁, для которой линия р₀ находится на ближайшем расстоянии. Если ошибки источников пеленгов неизвестны или они одинаковые, точкой цели можно считать середину отрезка между найденными точками. Если источники пеленгов имеют большую разницу точности определения направления, отрезок между найденными точками следует поделить пропорционально отношению среднеквадратичных ошибок этих источников в сторону точки той линии пеленга, для которой ошибки меньше.

Определение значения t

Для рассматриваемой задачи выражение (2) можно упростить. Если использовать не коэффициенты направляющего вектора, а направляющие косинусы линий пеленга, то знаменатель выражения (2) будет равен единице. Если значение t искать не для минимального d, а для квадрата этой величины, то скалярная форма для выражения (2) не будет иметь квадратного корня. С учетом этого для левой прямоугольной системы координат выражение для f(t) будет следующее:

где

cosa_x, cosa_y, cosa_h - направляющие косинусы опорного пеленга;

cosb_x, cosb_y, cosb_h - направляющие косинусы парного пеленга;

x₀ у₀ h₀ - координаты точки стояния источника опорного пеленга;

x₁ у₁ h₁ - координаты точки стояния источника парного пеленга.

Точка на линии опорного пеленга принимает значения:

x_t=x₀+tcosa_x;

y_t=у₀+tcosa_y;

h_t=h₀+tcosa_h.

Относительно искомой величины t выражение (3) преобразуется к виду:

где

a₁=cosa_hcosb_x-cosa_xcosb_h;

а₂=cosa_ycosb_h-cosa_hcosb_y;

а₃=cosa_xcosb_y-cosa_ycosb_x;

b₁=cosa_x(h₁-h₀)-cosa_h(x₁-x₀);

b₂=cosa_h(у₁-у₀)-cosa_y(h₁-h₀);

b₃=cosa_y(x₁-x₀)-cosa_x(у₁-у₀);

cosa_x=cos(E_a)cos(B_a);

cosa_y=cos(E_a)sin(B_a);

cosa_h=sin(E_a);

cosb_x=cos(E_b)cos(B_b);

cosb_y=cos(E_b)sin(B_b);

cosb_h=sin(E_b).

Значение функции f(t) будет минимальным, когда:

2(a₁ ²+а₂ ²+а₃ ²)t+2(a₁b₁+a₂b₂+a₃b₃)=0

Откуда:

где

А=a₁ ²+a₂ ²+а₃ ²

В=a₁b₁+a₂b₂+a₃b₃

Анализ результата решения

Величина t отрицательна. Знак t определяется только значением В, так как знаменатель (5) всегда положительный. При положительном В t имеет знак минус. Это означает, что линии пеленгов сближаются, но не в положительном направлении. В положительном направлении они расходятся. Это будет происходить в двух случаях. Первый - пеленги относятся к разным целям. Другой случай - пеленги относятся к одной цели, но слишком мала база измерения для тех ошибок, с которыми пеленги определяются. В обоих случаях использовать полученный результат для вычисления координат цели нельзя.

Величина t положительна, но слишком велика. Это будет в случае, когда линии пеленгов почти параллельны. Требуется дополнительный анализ такой ситуации. Если анализ показывает реальность такой большой дальности до цели, полученный результат используется.

Величина t положительна, но близка к нулю. Это будет в следующих случаях. Первый - редкий случай, когда пеленги случайно оказались параллельными. При этом расстояние между линиями пеленгов одинаково и равно базе измерений. Нельзя использовать полученный результат. Второй - цель оказалась близкой к точке стояния источника пеленга, для которого пеленг выбран как опорный. Требуется дополнительная проверка: сумма значений t для рассматриваемых двух пеленгов не должна быть меньше базы измерений. При выполнении проверки результат используется.

Определение координат цели по n пеленгам.

Если пеленгов цели больше двух, путем усреднения независимо полученных координат цели можно получить уточненные координаты цели.

Имеем n пеленгов цели от разных пеленгаторов. Выбирая каждый пеленг как опорный, и все оставшиеся (n-1) пеленгов как парные, по (5) получаем (n-1) отметок t_i на линии каждого пеленга. Вычисляем среднее значение t_si для каждого пеленга:

Вычисляем прямоугольные координаты точки на линии каждого пеленга:

x_ci=x_i+t_sicosa_xi;

y_ci=y_i+t_sicosa_yi;

h_ci=h_i+t_sicosa_hi.

Вычисляем прямоугольные координаты точки цели по значениям координат для n полученных точек:

Совместимость пеленгов

Совместимые пеленги - это пеленги от двух разных источников, которые потенциально могут принадлежать одной и той же цели. Первым условием совместимости является положительное значение t для двух пеленгов, то есть пеленги пересекаются в положительном направлении.

Другое условие совместимости пеленгов: расстояние между пеленгами в точке сближения не может превышать расчетное максимальное значение.

Максимальное расчетное расстояние между пеленгами p₁ и p₂:

d_r=δ_φ1·t₁+δ_φ2·t₂,

где δ_φ1, δ_φ2 - максимальное отклонение пеленга p₁ и пеленга р₂ по углу, определенные для пеленгаторов Р1 и Р2 для максимальных ошибок пеленгации.

Расстояние между точками линий пеленгов P_t1 и P_t2:

d=[(x_t1-x_t2)²+(y_t1-y_t2)²+(h_t1-h_t2]^1/2;

где координаты точки P_t1:

x_t1=x₁+t₁·cosa_x;

y_t1=у₁+t₁·cosa_y;

h_t1=h₁+t₁·cosa_h;

координаты точки P_t2:

x_t2=x₂+t₂·cosb_x;

y_t2=у₂+t₂·cosb_y;

h_t2=h₂+t₂·cosb_h.

Если определенное значение d превышает расчетное значение d_r, то пеленги несовместимы, точка сближения Ps - это ложная цель.

Разделение пеленгов по углу места

Разделение пеленгов по углу места дает дополнительную информацию для определения ложных целей. Определим угол между двумя пеленгами по углу места. Этот угол не может превышать некоторого максимального значения. Это значение определяется максимальным отклонением пеленга по углу места от направления на точку цели и равно сумме отклонений углов для двух пеленгов. Если найденное значение угла превышает максимальное значение, то даже для худшего сочетания отклонений пеленгов по углу места точка цели не может одновременно принадлежать двум пеленгам, точка Ps - это ложная цель. Определение значения угла между пеленгами приведено ниже.

Имеем:

P₁(x₁ у₁ h₁) - точка стояния источника пеленга P₁;

P₂(х₂ у₂ h₂) - точка стояния источника пеленга P₂;

P_s(x_s у_s h_s) - точка сближения пеленгов P₁ и P₂;

(cosa_x1cosa_y1cosa_h1) - направляющие косинусы линии пеленга P₁;

(cosa_x2cosa_y2cosa_h2) - направляющие косинусы линии пеленга P₂.

Уравнение плоскости, на которой лежат эти три указанные точки:

Ay+Bx+Ch-D=0

где А=x₁(h₂-h_s)-h₁(x₂-x_s)+(x₂h_s-h₂x_s);

В=h₁(y₂-y_s)-y₁(h₂-h_s)+(h₂y_s-y_sh_s);

С=у₁(x₂-x_s)-x₁(y₂-y_s)+(y₂x_s-x_sy_s);

D=у₁(x₂h_s-h₂x_s)-x₁(y₂h_s-y_sh₂)+h₁(y₂x_s-x₂y_s).

Пусть максимальная ошибка по углу места δ_е одинакова для пеленгов. Если δ_е равна нулю, то точка цели и оба пеленга лежат на плоскости. Если δ_е не равна нулю, то отклонение пеленгов от плоскости не может превысить δ_е и значение суммарного угла для двух пеленгов 2δ_е.

Углы пеленгов а1 и al с проекцией пеленгов на плоскости определяется по формуле:

sin(a1)=(A*cosa_y1+В*cosa_x1+С*cosa_h1)/sqrt(A²+B²+С²);

sin(a2)=(A*cosa_y2+В*cosa_x2+С*cosa_h2)/sqrt(A²+В²+С²).

Если оба пеленга имеют отклонения а1 и а2, лежат по разные стороны от плоскости, то угол между пеленгами, то есть сумма абсолютных значений а1 и а2, не может превышать 2δ_е.

Промышленная применимость

Данное предлагаемое изобретение промышленно реализуемо, обладает достаточной точностью получения координат для постановки целей на сопровождение, обеспечивает возможность работы оптоэлектронных станций обнаружения целей на стоянке и в движении, уменьшает общее время активного облучения целей триангуляционной системы.

При разработке и исследовании данной методики была создана цифровая модель оптоэлектронной станции. Проверка методики выполнена при постановке различных сценариев налета воздушных целей и различной установки станций на местности. Проверки показали актуальность решаемой задачи и преимущества предлагаемого способа.

Предлагаемый метод включается в состав алгоритмов комплекса программ «Триангуляция», предназначенного для решения задачи определения пространственных координат излучающего воздушного объекта по информации оптоэлектронных станций обнаружения объектов.

Литература

1. А.И.Куприянов, А.В.Сахаров. Теоретические основы радиоэлектронной борьбы. Москва. «Вузовская книга», 2007 г.

2. Г.Корн и Т.Корн. Справочник по математике для научных работников и инженеров. Москва. «Наука», 1974 г.

Способ триангуляции целей, реализуемый с помощью двух двухкоординатных пеленгаторов с координатами P₁(x₁, y₁, h₁) и P₂(x₂, y₂, h₂) точек стояния пеленгаторов, определяющих B₁, E₁ и В₂, Е₂ - азимут и угол места пеленга p₁ и р₂ и использующих эти данные для обработки с помощью средств вычислительной техники, отличающийся тем, что координаты цели определяются на стоянке носителей пеленгаторов и в движении, координаты двухкоординатных пеленгаторов задают в левой прямоугольной системе координат, пеленг цели задают точками стояния двух двухкоординатных пеленгаторов и направлением на цель из точек их стояния, при этом один из пеленгаторов p₁ выбирают «опорным», а другой р₂ «парным» к опорному, затем считают пеленг p₂ опорным, a p₁ парным к опорному и для обоих случаев повторяют аналогичные вычисления в виде:шаг 1 - определяются направляющие косинусы cosa_x, cosa_y, cosa_h линии пеленга p₁ и направляющие косинусы cosb_x, cosb_y, cosb_h линии пеленга p₂:для пеленга p₁:cosa_x=cos(E₁)cos(B₁);cosa_y=cos(E₁)sin(B₁);cosa_h=sin(E₁);для пеленга р₂:cosb_x=cos(E₂)cos(B₂);cosb_y=cos(E₂)sin(B₂);cosb_y=sin(E₂),шаг 2 - определяется расстояние t₁ от точки стояния пеленгатора Р1 до точки Р_t1 на линии пеленга p₁, для которой расстояние до линии пеленга p₂ минимальное: ,где a₁=cosa_hcosb_x-cosa_xcosb_h;a₂=cosa_ycosb_h-cosa_hcosb_y;a₃=cosa_xcosb_y-cosa_ycosb_x;b₁=cosa_x(h₂-h₁)-cosa_h(x₂-x₁);b₂=cosa_h(y₂-y₁)-cosa_y(h₂-h₁);b₃=cosa_y(x₂-x₁)-cosa_x(y₂-y₁);шаг 3 - определяется расстояние t₂ от точки стояния пеленгатора Р2 до точки Р_t2 на линии пеленга р₂, для которой расстояние до линии пеленга p₁ минимальное: где a₁=cosb_hcosa_x-cosb_xcosa_h;a₂=cosb_ycosa_h-cosb_hcosa_y;a₃=cosb_xcosa_y-cosb_ycosa_x;b₁=cosb_x(h₂-h₁)-cosb_h(x₂-x₁);b₂=cosb_h(y₂-y₁)-cosb_y(h₂-h₁);b₃=cosb_y(x₂-x₁)-cosb_x(y₂-y₁);шаг 4 - определяются координаты точки P_t1 и точки Р_t2:координаты точки Р_t1:x_t1=x₁+t₁·cosa_x;y_t1=y₁+t₁·cosa_y;h_t1=h₁+t₁·cosa_h;координаты точки Р_t2:x_t2=x₂+t₂·cosb_x;y_t2=y₂+t₂·cosb_y;h_t2=h₂+t₂·cosb_h;шаг 5 - вычисляется значение признака С_р совместимости пеленгов p₁ и р₂:расстояние между точками Р_t1 и P_t2:d=[(x_t1-x_t2)²+(y_t1-y_t2)²+(h_t1-h_t2)²]^1/2;максимальное возможное расстояние между пеленгами p₁ и р₂:d_r=δ_φ·t₁+δ_φ·t₂,где δ_φ - максимальное угловое отклонение пеленгов от точки цели, определенное для пеленгаторов для максимальных ошибок пеленгации;если значения t₁ и t₂ положительные и если значение d меньше d_r, то значение признака С_р устанавливается 1, иначе 0;при нулевом значении признака С_р пеленги несовместимы, определение координат точки P_s (шаг 6) не выполняется и точку сближения пеленгов Ps считают ложной целью;шаг 6 - определяются выходные данные - координаты точки P_s на отрезке Р_t1Р_t2, для которой расстояние до линии пеленга p₁ и до линии пеленга р₂ минимальное:x_s=(x_t1·t₁+x_t2·t₂)/(t₁+t₂);y_s=(y_t1·t₁+y_t2·t₂)/(t₁+t₂);h_s=(h_t1·t₁+h_t2·t₂)/(t₁+t₂);по результатам проведенных вычислений определяют координаты цели и ставят цель на сопровождение.