Способы спектрального анализа

Способы спектрального анализа

Иллюстрации

Показать все

Реферат

Область техники изобретения

Изобретение относится к спектральным устройствам и способам. Оно, в частности, применимо в спектроскопии Рамана, хотя также может быть использовано в других способах спектроскопии, например, использующих узколинейную фотолюминесценцию, флуоресценцию, катодолюминесценцию или инфракрасное излучение.

Описание известного уровня техники

Эффект Рамана представляет собой явление, при котором образец рассеивает падающий свет данной частоты в частотном спектре, линии которого вызваны взаимодействием падающего света с молекулами, входящими в состав образца. Различные химические соединения имеют различные характеристики спектра Рамана, и таким образом этот эффект может быть использован для анализа имеющегося химического образца.

Примеры рамановских спектральных приборов известны из патентов США №5,442,438 и 5,510,894, которые приведены здесь в качестве ссылок. Образец облучается монохроматическим светом от лазера. Как правило, рассеянный свет затем диспергируется в спектр Рамана дисперсионным устройством, таким как дифракционная решетка, например, в монохроматоре. Диспергированный спектр регистрируется детектором, таким как прибор с зарядовой связью (CCD). Затем полученные данные могут быть введены в компьютер для анализа.

Когда должна быть проанализирована двухмерная поверхность образца, спектральные данные могут быть получены для нескольких точек, расположенных по поверхности. В соответствии с анализом спектральных данных, затем с помощью компьютера могут быть сделаны изображения, представляющие карту распределения различных соединений на поверхности образца. Следующее обсуждение относится к анализу фармацевтических образцов, но будет понятно, что оно в равной степени применимо для многих других типов образцов.

Данные гиперспектрального изображения, такие, которые можно получить из экспериментов рамановского картирования, могут быть использованы для того, чтобы получить изображения распределения различных соединений, присутствующих в фармацевтических образцах. Создание этих изображений может быть сложной задачей. В одномерных методах отбираются частоты с допущенными интенсивностями, которые получены от одного соединения, и изображения создаются из отклонений интенсивностей на этих частотах. Эти методы требуют знания присутствующих в образце соединений и их чистых спектров, и в случае, если спектры перекрываются, возникают проблемы и никакие интенсивности на частоте не могут быть четко приписаны ни к одному спектру. Последняя проблема может быть преодолена путем использования классического прямого многомерного метода наименьших квадратов (DCLS). Чтобы создать изображения распределений, здесь используются эталонные спектры. Однако если имеются неполные знания или ничего не известно о присутствующих соединениях, то этот метод не может быть успешно использован. Требуется способ, которым можно определить, какие соединения присутствуют в гиперспектральных данных, чтобы можно было создать изображения распределений.

Многомерные способы разрешения кривых (MCR) могут разрешать чистые спектры и соответствующие концентрации из смесей и применяются для гиперспектральных данных, чтобы создать распределительные изображения. Один такой метод представляет собой альтернативную оптимизацию методом наименьших квадратов (ALS), которая была разработана для выделения данных, так, как получается в анализах хроматографии. Получают первоначальные оценки либо чистых спектров, либо концентраций, и несколько раз оптимизируют путем перерасчетов при ограничительном условии, таком как неотрицательность.

Чтобы определить первоначальные оценки, используются разнообразные методы. Некоторые из них были разработаны, чтобы использовать выделение свойств набора данных (например, эволюционный факторный анализ (EFA), фиксированный размер следящего окна - эволюционный факторный анализ (FSW-EFA), и факторный анализ окна), но они не очень хорошо подходят для анализа изображений. Для анализа изображений первоначальные оценки могут быть определены из анализа главных компонент (РСА) или РСА, сопровождаемого Варимакс-ротацией. Методы, такие как ортогональное проецирование (ОРА) и простой в исполнении самомоделирующий анализ смеси в интерактивном режиме (SIMPLISMA), определяют наиболее чистые спектры или частоты из набора данных, и их результаты могут быть затем использованы, для того чтобы инициировать оптимизацию ALS. При использовании спектральных оценок из набора данных, как вводных для работ алгоритма ALS, хорошо обеспеченные компонентные спектры представляются в наборе данных почти в чистом виде. С другой стороны, значения интенсивности на частоте обеспечивают хорошую оценку для концентраций компонента, если они без сомнения могут быть отнесены к полосе Рамана компонентного спектра.

Наборы данных рамановского изображения часто очень сложны, и указанные выше условия часто остаются справедливыми только для нескольких основных компонентов. Второстепенные компоненты могут иметь очень низкие сигнальные уровни и встречаются только в малых соотношениях в любом из спектров. При использовании спектральных оценок в качестве вводных в алгоритм ALS, алгоритм часто не может улучшить эти спектры, и разрешенные спектры все еще содержат элементы от других компонентных спектров. Для сложных многокомпонентных систем полосы Рамана от различных соединений часто в значительной степени перекрываются. Перекрывание между полосами ведет к избыточному моделированию спектров, когда алгоритм ALS инициируется оценками концентраций, то есть разрешенные спектры показывают впадину там, где другой разрешенный спектр имеет пик, и разрешение изображений соответствующих концентраций ухудшается.

Другая проблема для общепринятых алгоритмов MCR может быть вызвана небольшими изменениями, которые встречаются в спектрах Рамана из-за ориентации кристаллов, нагревания образца или ошибок приборов. Для полного анализа и разрешения всех химических компонентов они должны быть включены в анализ, но они не должны мешать разрешению основных компонентов. Если все компоненты моделируются одновременно, им придается равный вес; тогда сигнал от основных компонентов имеет тенденцию моделироваться во второстепенные компоненты. В таких случаях модель является неустойчивой в отношении основных компонентов и становится трудной для интерпретации.

Сущность изобретения

Один объект настоящего изобретения обеспечивает способ определения компонентов, присутствующих в образце, содержащий этапы:

отбор спектральных данных для некоторого количества точек на образце;

осуществление первоначальной оценки спектральных значений первого компонента образца;

исходя из оценки первого компонента, выполнение итеративного разрешения спектра первого компонента; и

осуществление первоначальной оценки спектральных значений, по меньшей мере, еще одного компонента образца, и выполнение итеративного разрешения спектра каждого такого компонента, исходя из соответствующей первоначальной оценки и из одного или более разрешенных ранее спектров.

Второй объект изобретения обеспечивает способ спектрального определения компонентов, присутствующих в образце, содержащий этапы:

освещение образца;

отбор спектральных данных для некоторого количества точек на образце;

осуществление первоначальной оценки спектральных значений первого компонента образца;

исходя из оценки первого компонента, выполнение итеративного разрешения спектра первого компонента; и

осуществление первоначальной оценки спектральных значений, по меньшей мере, еще одного компонента образца, и выполнение итеративного разрешения спектра каждого такого компонента, исходя из соответствующей первоначальной оценки и из одного или более разрешенных ранее спектров.

Предпочтительно, чтобы применялись равные величины для всех спектральных значений соответствующих первоначальных оценок. Предпочтительно, чтобы на этапах итеративного разрешения применялась альтернативная оптимизация методом наименьших квадратов.

Компоненты могут быть проанализированы, как указано выше, для получения карты, представляющей концентрации компонентов образца на его поверхности.

Другой объект изобретения обеспечивает устройство для спектрального анализа, оборудованное таким образом, чтобы выполнить указанный выше способ. Устройство соответственно включает компьютер с программным управлением для выполнения этапов итеративного разрешения спектров компонентов, исходя из первоначальных оценок.

Другие объекты изобретения обеспечивают код компьютерной программы, содержащий инструкции, согласно которым компьютер выполняет эти этапы; и машиночитаемый носитель, содержащий такой код.

В способе изобретения, итеративно разрешенные спектральные значения компонентов могут соответствующим образом сохраняться, как только они достигли разрешения, соответственно в компьютерном исполнении этапов итеративного разрешения.

Краткое описание чертежей

Предпочтительные способы, устройства и примеры по изобретению будут теперь описаны со ссылками на сопровождающие чертежи, на которых:

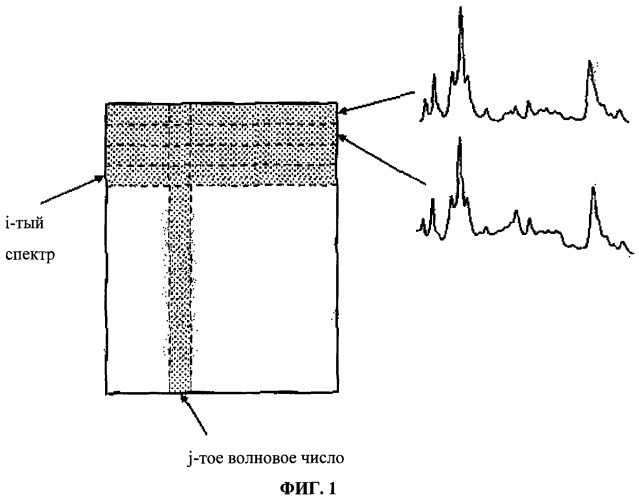
На Фиг.1 показано расположение гиперспектральных данных в матрице.

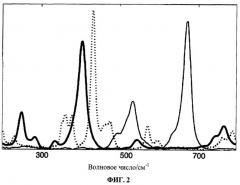
На Фиг.2 показаны спектры, использованные для имитации набора смешанных

данных для примера I: спектр компонента 1 (толстая линия), спектр компонента 2 (тонкая линия), спектр компонента 3 (пунктирная линия).

На Фиг.3 показаны компонентные спектры изображенной смеси примера I для компонент 1, 2 и 3: эталонные спектры (толстая линия), спектры, разрешенные пустым моделированием (линия средней толщины), спектры, разрешенные методом ОРА(конц) / MCR-ALS (тонкая линия), спектры, разрешенные методом ОРА(спек) MCR-ALS (пунктирная линия).

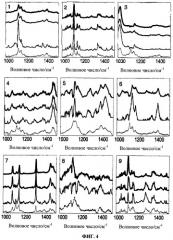
На Фиг.4 показаны спектры порошкового образца примера II: эталонные спектры (там, где имеются) (толстая линия), спектры, разрешенные методом пустого моделирования (линия средней толщины), спектры, разрешенные методом ОРА(конц) / MCR-ALS (тонкая линия), спектры, разрешенные методом ОРА(спек) MCR-ALS (пунктирная линия). Эталонный спектр лактозы показан для компоненты 2 и 9.

На Фиг.5 показаны изображения концентраций из примера II, полученные с применением метода «пустого моделирования» в соответствии с настоящим изобретением.

На Фиг.6 показаны значения спектральных корреляций для различных номеров разрешенных компонент в примере II, (а) целлюлоза (компонента 1), (b) лактоза (компонента 2), (с) АФИ (компонента 4), (d) стеарат магния (компонента 7). Значения в случае пустого моделирования (толстая линия), значения в случае метода ОРА(конц) / MCR-ALS (тонкая линия), значения в случае метода ОРА(спек) / MCR-ALS (пунктирная линия).

На Фиг.7 показан спектр целлюлозы, разрешенный методом ОРА(конц) / MCR-ALS в примере II. Эталонный спектр (толстая линия), спектр, разрешенный в модели с 7 компонентами (тонкая линия), спектр, разрешенный в модели с 10 компонентами (линия средней толщины).

На Фиг.8 показаны спектры таблетки ранитидина из примера III: эталонный спектр целлюлозы (толстая линия), спектры, разрешенные способом пустого моделирования (линия средней толщины), спектры, разрешенные методом ОРА(конц) / MCR-ALS (тонкая линия), спектры, разрешенные методом ОРА(спек) MCR-ALS (пунктирная линия).

На Фиг.9 показаны профильные изображения концентраций из таблетки ранитидина из примера III, первый ряд: компонента 1 (АФИ), второй ряд: компонента 2 (целлюлоза), третий ряд: компонента 3 (изменения интенсивности в лекарственном пике).

Фиг.10 представляет собой схематическое изображение микроскопа Рамана.

Описание предпочтительных вариантов выполнения изобретения

Предпочтительный аналитический способ, разработанный авторами изобретения, представляет собой новый метод альтернативной оптимизации по наименьшим квадратам, в котором разрешение компонент осуществляется последовательно. Поскольку применяются равные величины для всех переменных (спектральные значения) соответствующих первоначальных оценок, мы говорим об этом, как о «пустом моделировании». Предпочтительные осуществления нового способа являются простыми в применении и приводят к модели, которая способна осуществлять разрешение чистых спектров второстепенных компонентов, в то же время, оставаясь очень стабильной по отношению к основным компонентам (например, сигнал от основных компонентов не моделируется во второстепенные компоненты), но также позволяя их итеративное улучшение. Предпочтительный способ был применен к имитационным данным (пример I), а также к данным рамановского гиперспектрального изображения в случае фармацевтических образцов (примеры II и III), и его функциональную характеристику сравнивали с исходным методом MCR-ALS, когда применяли оценки спектров или концентраций, полученных методом ОРА, чтобы инициировать способ. Метод РСА применялся во всех этих случаях для определения числа компонент, чтобы осуществить разрешение и удалить шум из набора данных.

Экспериментальные методы

Данные для приведенных ниже примеров II и III были получены с помощью Via Reflex микроскопа Рамана, поставляемого промышленно настоящим заявителем/ патентообладателем Renishaw, оборудованного термоэлектрически охлаждаемым приемником излучения RenCam CCD. В обоих случаях применялся 10х объектив совместно с 785 нм лазерным возбуждением и решетка 1200 линий на мм в качестве диспергирующего элемента. Пример II представляет собой данные эксперимента картирования с точечной фокусировкой, и пример III представляет собой данные эксперимента картирования со штриховой фокусировкой. Оба метода представляют собой способы гиперспектрального изображения. В результате получают куб гиперспектрального изображения, содержащий спектральные значения от каждого двухмерного массива точек на образце. В случае картирования с точечной фокусировкой, один спектр отбирается на отдельно взятой точке образца для набора, и это повторяется для каждой точки массива. В случае картирования со штриховой фокусировкой, на образце фокусируется спектральная линия излучения лазера, и получается несколько спектров от соседних точек образца в отдельно взятом наборе данных, что приводит к значительному преимуществу по времени по сравнению с изображением с точечной фокусировкой.

Используемый микроскоп Рамана представляет собой устройство, как описано в патенте США No. 5,442,438 и представлено схематически на Фиг.10 в сопровождающих чертежах. Входящий лазерный луч 10 отражается под углом 90 градусов дихроичным фильтром 12, расположенным под углом 45 градусов к оптическому пути. Голографический дихроичный фильтр может быть расположен иначе, под небольшим углом к падающему свету, таким как 10 градусов. Лазерный луч затем проходит к линзе 16 объектива микроскопа, которая фокусирует его на пятне на его фокальной точке 19 на образце 18. Свет рассеивается образцом на этом освещенном пятне и собирается линзой 16 объектива микроскопа и коллимируется в параллельный пучок лучей, который проходит обратно к дихроичному фильтру 12. Фильтр 12 отражает рассеянный релеевский свет, имеющий ту же самую частоту, как и входящий лазерный луч 10, и пропускает рамановский рассеянный свет. Рассеянный свет Рамана затем проходит к анализатору 20 Рамана.

Анализатор 20 Рамана содержит диспергирующий элемент, такой как дифракционная решетка. Свет от анализатора 20 фокусируется линзой 22 на соответствующий фотодетектор. Двухмерный массив фотодетектора является предпочтительным. В настоящем варианте выполнения изобретения, RenCam детектор 24 представляет собой прибор с зарядовой связью (CCD), состоящий из двухмерного массива элементов изображения, и который соединяется с компьютером 25, который получает данные от каждого из элементов и анализирует по мере необходимости. Анализатор 20 производит спектр, имеющий различные полосы, как указано пунктирными линиями 28, расходящимися по линии вдоль CCD 24.

Образец 18 может быть установлен на столе X-Y так, что фокальная точка 19 может быть сканирована параллельно ему в направлениях Х и Y, например, под контролем компьютера. Затем на каждой точке образца отбирается по одному спектру на одно данное (Пример II). Это дает возможность картирования поверхности образца. Фокальная точка 19 может быть также передвинута в глубину, либо путем перемещения образца 18, либо линзы 16 вдоль оптической оси. Снова, это может быть осуществлено под контролем компьютера 25.

Поскольку детектор 24 является двухмерным, можно также получать спектры от нескольких точек образца одновременно, путем фокусировки лазера на линии образца ортогонально к направлению диспергирования спектра (Пример III). Несколько спектров от соседних точек вдоль линии считываются с неспектрального измерения CCD в отдельных данных, что приводит к значительному преимуществу во времени по сравнению с картированием с точечной фокусировкой.

Компьютер 25 может быть также обеспечен кодом к программному обеспечению на соответствующем носителе, содержащем инструкции для выполнения аналитических процедур, описанных в этой инструкции. В качестве альтернативы, как описано ниже, полученные спектральные данные могут быть перенесены на отдельный компьютер, имеющий такое программное обеспечение для этого анализа. В любом случае, когда анализ продолжается, значения разрешенных спектров компонентов хранятся в указанном компьютере и в дальнейшем могут быть обработаны и выданы или высвечены на экране в виде карт, показывающих концентрации компонентов в образце.

Пример I: имитационные спектры смеси

Чтобы создать матрицу из 2500 смешанных спектров (Фиг.2), были добавлены чистые спектры Рамана трех пигментов в различных соотношениях. Средняя, минимальная и максимальная доля каждого пигментного спектра даны в Таблице 1. Спектры 1 и 2 присутствовали по всему набору данных, в то время как спектр 3 присутствовал только в 100 случаях, чтобы имитировать второстепенный компонент. К набору данных был добавлен случайный шум, в соответствии со статистикой Пуассона, чтобы имитировать ошибки, возникающие в результате шума. Спектры, использованные для создания набора данных, были нормализованы путем вычитания минимальных значений и деления на сумму их интенсивностей. Это устраняет неоднозначности интенсивностей из набора данных и облегчает прямое сравнение с методами ALS.

Пример II: фармацевтический порошок

Анализируемый образец представлял собой порошковую смесь, которая содержала 1% активного фармацевтического ингредиента (АФИ) и 99% вспомогательных средств, включающих целлюлозу, лактозу и дикальцийфосфат. Поверхность образца была выровнена, и была получена карта поверхности с точечной фокусировкой. Площадь этой карты составляла 600 µм × 66 µм с шаговым размером 6 µм, представляя 1,212 собранных спектров.

Пример III: таблетка ранитидина

Была проанализирована промышленно доступная таблетка, содержащая 75 мг ранитидина в качестве АФИ. АФИ составлял приблизительно 50% от общей массы таблетки. Вспомогательные средства, присутствующие внутри таблетки, представляли собой микрокристаллическую целлюлозу и стеарат магния. Таблетка была разрезана скальпелем по горизонтали. Карта с линейной фокусировкой была собрана с площади 1.68 мм × 1.95 мм. При размере шага 6 µм по оси x и при свойственном размере шага 5,81 µм по оси y, это дало 94,000 собранных спектров.

Теоретические основы

Для хемометрического анализа куб гиперспектрального изображения разворачивается в матрицу Х так, что каждый отобранный спектр занимает ряд данных в матрице (Фиг.1). Матрица имеет размеры I×J, где I представляет собой общее количество спектров из набора данных, и J представляет собой количество переменных, которые представляют собой частоты, на которых были отобраны интенсивности. Целью разрешения кривой является разложение этой матрицы в физически значимые подматрицы С и S:

Для набора данных, моделированных в соответствии с n компонентами, С представляет собой матрицу I×n, где каждая колонка соответствует значениям концентрации компоненты, и S представляет собой матрицу J×n, где каждая колонка представляет компонентный спектр. Е представляет собой матрицу остатков с теми же самыми размерами, как и X. Способы разрешения кривой подыскиваются таким образом, чтобы минимизировать значения в этой матрице.

Определение числа компонент

В анализе главных компонент матрица Х разлагается на счета и нагрузки, которые представляют главные компоненты (PCs):

Счета Т и нагрузки V представляют собой линейные комбинации С и S^Т, но они не представляют собой физически значимых решений Уравнения 1, то есть главные компоненты не представляют химические компоненты. Главные компоненты ортогональны друг к другу и рассчитываются так, что каждая компонента объясняет, насколько возможна данная дисперсия. Поэтому, в случае, если данные хорошо моделируются в соответствии с n компонентами, первые n главных компонент будут представлять сигнал, и последующие компоненты просто показывают шум.

Число n может быть определено из дисперсии, которую объясняет каждая компонента: как только компоненты показывают только шум, данная дисперсия, объясненная каждой компонентой, падает до сравнительно постоянного значения. Для данных Рамана, однако, мы нашли, что более надежно применять автокорреляционные значения нагрузок, чтобы определить, показывают компоненты спектральные характеристики или шум. Это возможно, поскольку наборы данных представляют собой избыточные замеры в частоте, и таким образом сигнальные уровни на соседних частотах в спектре являются скоррелированными.

Межэлементные корреляции векторов нагрузок рассчитываются как

где v_k представляет собой вектор нагрузок k-той PC. Для значений, близких к единице, точки высоко скорреллированы, и главная компонента показывает сигнал. Для значений, близких к нулю, корреляция низкая, и главная компонента показывает шум. Кривая зависимости автокорреляционных значений от числа PC показывает острый спад при n. Все главные компоненты после n могут быть отбракованы, и Х может быть пересчитана из первых n PC, чтобы получить отфильтрованный от шума набор данных.

Выбор первоначальных оценок

Чтобы получить первоначальные оценки для спектров, а также для концентраций, можно применять метод ортогонального проектирования. Самые чистые спектры и частоты (переменные величины) в наборе данных определяются нахождением таких, которые являются в наибольшей степени неоднородными. Коэффициент неоднородности между двумя рядами векторов, входящих в матрицу Y_i, дается уравнением:

Когда для нахождения чистого спектра применяется метод ОРА, Y_i представляет собой матрицу, содержащую средний спектр из Х и i-тый спектр образца:

Коэффициент неоднородности рассчитывается для каждого спектра в наборе данных, и спектр с самым высоким значением k определяется как первый компонентный спектр.

Средний спектр затем заменяется этим спектром в:

Коэффициенты пересчитываются согласно Уравнению 4 для определения следующего наиболее чистого спектра, и матрица расширяется, чтобы включить этот второй компонентный спектр. Эта процедура повторяется до тех пор, пока требуемое число самых чистых спектров не будет найдено.

Чтобы найти чистые частоты, а не чистые спектры, может быть применен тот же самый метод. Коэффициенты неоднородности тогда рассчитываются для колонок Х (частоты), а не рядов (спектры).

MCR-ALS

В альтернативной оптимизации методом наименьших квадратов, применяется оценка либо S, либо С, чтобы решить Уравнение 1 для другого неизвестного, при этом решение ограничивается, так чтобы обеспечить физически значимый результат. Это решение затем применяется для перерасчета улучшенного значения для оцениваемой матрицы с ограничивающим условием физической значимости, как указано выше. Этот процесс повторяется до тех пор, пока модель не сходится. При испытаниях на сходимость, мы применяем процентную долю неадекватности (lack of fit) (lof), которая рассчитывается, используя Уравнение 5.

Говорят, что итерация сошлась, когда изменение неадекватности между двумя последовательными итерациями меньше, чем пороговая величина.

Ограничения, которые могут быть применены, зависят от типа данных. Неотрицательность концентраций и/или спектров является наиболее общим ограничением, и оно применимо в большинстве случаев. Это может быть достигнуто путем получения решения для Уравнения 1 методом наименьших квадратов, что минимизирует Е, и путем сведения всех отрицательных значений в решении к нулю. Уравнение 1 также может быть решено с применением алгоритма неотрицательности при среднеквадратичной оценке, такой как линейное среднеквадратичное оценивание при ограничительном условии неотрицательности (NNLS), или быстрый среднеквадратичный метод при ограничительном условии неотрицательности (FNNLS). Эти алгоритмы обеспечивают превосходное решение, так как они гарантируют, что решение методом наименьших квадратов происходит при ограничительном условии неотрицательности. В дополнение, концентрации могут быть ограничены аддитивностью к единице, так что для точки образца сумма всех значений концентраций представляет собой единицу. Ограничения по одномодальности (то есть один относительный максимум в концентрациях компонента) и избирательности (например, окна нулевой концентрации) были применены также для данных хроматографии, но они обычно не применяются для данных изображения путем спектроскопии.

Пустое моделирование

Для алгоритма пустого моделирования создается «пустой спектр» как оценка для первого компонентного спектра. Этот пустой спектр имеет равными все интенсивности, со значением, зависящим от нормализации спектра в X. Чтобы моделировать первый компонентный спектр, применяется оптимизация ALS. Неотрицательность С и S усиливается при применении алгоритма FNNLS, и разрешенный спектр представляет собой длину, ограниченную до значения в соответствии с нормализацией матрицы данных. В следующей итерации применяются разрешенный спектр плюс другой пустой спектр, чтобы повторно инициализировать оптимизацию ALS. Применяются те же самые ограничения, и концентрации так же ограничиваются аддитивностью к единице. После каждой итерации добавляется другой пустой спектр, до тех пор, пока все значащие компоненты не будут разрешены. Концентрации и спектры, полученные в последней оптимизации, представляют собой окончательное решение пустого моделирования.

Ступенчатое разрешение компонентных спектров подразумевает, что компоненты не являются эквивалентными, то есть имеются основные и второстепенные компоненты. Первый компонент будет моделироваться в средний спектр в первой итерации и оптимизироваться, чтобы показать спектр основного компонента позже. Для того чтобы осуществить этот процесс, приемлемое изображение спектра основного компонента должно быть представлено почти в чистом виде в наборе данных.

Методы анализа

Хемометрический анализ наборов данных из выше приведенных Примеров выполняли в MATLAB R2006a (The MathWorks Inc., Natick, MA). В Примерах I и II применяли HP Compaq dc5100 компьютер с 32-бит, 2.8 ГГц процессором Pentium 4 и 1.25 Гб физической памяти, работающий под управлением Microsoft Windows XP Professional. Пример III анализировали, с применением 64-бит версии MATLAB R2006a на Evesham PC с 64-бит, 2.01 ГГц AMD Athlon 64 x2 двухъядерным 3800 + процессором и 512 Мб физической памяти, работающего под управлением Microsoft Windows XP Professional x64. Применение увеличенного адресного пространства в этой структуре потребовалось для того, чтобы анализировать больший набор данных в примере III.

Характерные признаки космических лучей удаляли из наборов данных II и III, применяя метод сравнения ближайших соседей. РСА выполнялся для всех наборов данных, чтобы определить число компонент и удалить шум. Полученные спектры обрабатывали путем вычитания минимального значения каждого спектра и шкалирования до единичной суммы интенсивностей. Это делалось для того, чтобы удалить различия интенсивностей, например, из-за изменений мощности лазера или фокуса. Это гарантирует, что аддитивность к единице концентраций представляет собой возможное ограничение. Оценки концентраций и чистых спектров получали методом ОРА. Окончательные компонентные спектры и концентрации моделировали методом MCR-ALS, используя оценки концентраций из ОРА, чтобы инициировать оптимизацию (ОРА(конц)/МСК-ALS), методом MCR-ALS, используя спектры из ОРА (OPA(спек)/MCR-ALS) и пустым моделированием. Во всех случаях, как спектры, так и концентрации, были ограничены условием неотрицательности, применяя алгоритм FNNLS. Концентрации были ограничены аддитивностью к единице, и спектры были ограничены единичной суммой интенсивностей.

Когда использовались эталонные спектры, результаты различных алгоритмов, сравнивали путем расчета коэффициентов корреляции (Уравнение 6) между среднецентрированными разрешенными спектрами (s_k) и среднецентрированными эталонными спектрами (s_r).

Для имитационных данных примера I действительные значения концентраций известны и могут быть использованы для сравнения различных подходов. Поэтому в этом случае были рассчитаны средние квадратичные отклонения разрешенных концентраций от их известных значений

Результаты и обсуждение

Пример I: имитационные спектры смеси

РСА ясно показывает, что в наборе данных, как и ожидалось, имеются 3 компоненты. Эталонные спектры и компонентные спектры, которые были разрешены различными методами MCR, показаны на Фиг.3. Несколько сравнений моделей даны в Таблице 1. Спектр компоненты 1, разрешенный методом OPA(спек)/MCR-ALS, хорошо соответствует эталонному спектру, но два других компонентных спектра также показывают признаки первого. Сопутствующее этому обстоятельство представляет собой смещение концентрации от компоненты 1 к двум последним, приводя к плохой предсказуемости значений концентраций.

С применением метода ОРА(конц) / MCR-ALS все спектры очевидно достаточно хорошо разрешаются, хотя корреляция спектра компоненты 1 с эталонным спектром имеет порядок величины хуже, чем при разрешении этого спектра двумя другими методами. Худшее разрешение этого спектра в наибольшей степени заметно по слабой впадине с краю высокого волнового числа его основной полосы Рамана на 400 см^-1. На этом краю полоса перекрывается самой сильной полосой в спектре компоненты 3, и поэтому спектр компоненты 1 избыточно моделируется. Это сильно отражается на значениях концентрации. Область значений концентраций первой компоненты является слишком узкой, и ее средняя концентрация также является низкой. В случае компоненты 3, среднее квадратичное отклонение концентраций от известных значений очень высоко по сравнению со средним отношением. Минимальное значение концентрации для этой компоненты составляет 2.13%, даже если эта компонента присутствует только в 100 спектрах из 2500, и средняя концентрация представляется слишком высокой, больше, чем в шесть раз. Таким образом, несмотря на хорошую корреляцию спектральных значений, концентрации компонентов 1 и 3 разрешаются не очень хорошо, и изображения концентраций не будут отражать действительного распределения. С другой стороны, в случае компоненты 2, для которой основные полосы Рамана хорошо отделяются от полос Рамана других компонентных спектров, как спектры, так и концентрации хорошо соотносятся с эталонным спектром и действительными значениями концентраций.

В случае пустого моделирования все компонентные спектры хорошо разрешаются, в частности спектр первой компоненты. Это также приводит к низким среднеквадратичным отклонениям разрешенных концентраций от их известных значений. Отдельно от случая компоненты 2, разрешенной методом ОРА(конц) / MCR-ALS, все среднеквадратичные отклонения концентраций лучше в случае результатов пустого моделирования, чем для результатов, полученных другими методами. Поэтому полученные концентрации более точно отражают реальные значения.

Пример II: Фармацевтический порошок

Анализ главных компонент карт данных, показал, что в наборе данных присутствуют десять компонент. Десять компонент были разрешены тремя способами MCR-ALS, как описано ранее. Результаты различных методов показаны в Таблице 2. Первые девять разрешенных спектров, которые сравнивали с эталонными спектрами, там, где таковые имеются, даны на Фиг.4, и изображения, полученные пустым моделированием, даны на Фиг.5.

Результаты пустого моделирования могут быть объяснены следующим образом. Имеются шесть компонент, которые являются независимыми соединениями: целлюлоза (компонента 1), лактоза (компонента 2), дикальцийфосфат (компонента 3), АФИ (компонента 4), неидентифицированное вспомогательное вещество (компонента 5) и стеарат магния (компонента 7). Компоненты 6, 8 и 10 происходят из базовых отклонений. Компонента 9 является следствием отклонений различных вращательных состояний между двумя кристаллами лактозы (сравнить изображения компоненты 2 и 9 на Фиг.5).

Эти наблюдения менее очевидны из результатов метода ОРА(спек) / MCR-ALS. Целлюлоза и лактоза разрешаются очень хорошо (даже лучше, чем пустым моделированием, из-за перекрывания между пиками двух спектров), однако разрешение второстепенных компонентов представляется плохим. Все разрешенные спектры дикальцийфосфата, АФИ и стеарата магния содержат характерные признаки спектра целлюлозы, так же как и компоненты, которые обнаруживают базовые изменения в анализах пустого моделирования. Это плохое разрешение приводит к смещению в значениях средней концентрации, по сравнению с теми же значениями, полученными путем пустого моделирования. Первая компонента имеет значительно более низкую концентрацию в случае модели ОРА(спек) / MCR-ALS, в то время как другие значения средней концентрации оказываются выше, чем те же значения в случае пустого моделирования.

Дикальцийфосфат и АФИ хорошо разрешаются методом ОРА(конц) / MCR-ALS, но сигнал от целлюлозы моделируется, по меньшей мере, в две компоненты (1 и 6), и совпадение с эталонным спектром целлюлозы является плохим. Что касается модели с 10 компонентами, то результаты метода ОРА(конц) / MCR-ALS могут быть использованы для доказательства присутствия лактозы, дикальцийфосфата и АФИ, но соответствующие изображения концентраций характеризуются низкой контрастностью и трудны для интерпретации. Значения концентраций наводят на мысль, что, по меньшей мере, 8 компонент присутствуют в каждой точке карты, в то время как результаты пустого моделирования говорят о том, что основной компонент (целлюлоза) присутствует везде, при этом второстепенные компоненты присутствуют только в локализованных частицах (см. Таблицу 2 и Фиг.5). Хорошее разрешение спектра целлюлозы методом пустого моделирования позволяет предположить, что это является истиной, и что концентрации по методу ОРА(конц) / MCR-ALS, вероятно, являются неточными (как в примере I).

Относительно широкий набор присутствующих компонент вызывает часть проблемы разрешения для ОРА(конц) / MCR-ALS. Никакие истинно чистые частоты не могут быть выделены для последних компонент, поскольку они обусловлены базовыми изменениями, и между оценками имеется широкое перекрывание. Это является причиной того, что конечные значения концентрации сигнального спектра разделяются между компонентами, и реальные спектры становятся линейными комбинациями разрешенных компонентных спектров. Для сравнения, все методы были повторены с различным числом компонент (от 1 до 10). Корреляционные значения разрешенных спектров целлюлозы, лактозы и АФИ и эталонные спектры стеарата магния показаны на Фиг.6. Для лактозы и АФИ корреляционные значения упали, как только компонент был разрешен, и затем оставались относительно постоян