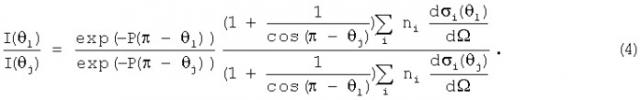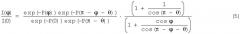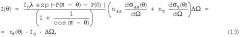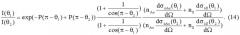Способ определения концентрации элементов в твердом теле

Способ определения концентрации элементов в твердом теле

Иллюстрации

Показать все

Реферат

Изобретение относится к области элементного анализа приповерхностного слоя многокомпонентного вещества и может найти применение для неразрушающего контроля компонентного состава приповерхностного слоя твердого тела, позволяющего определять распределения концентраций отдельных компонент с разрешением по глубине при известном элементном составе.

Известны способы, позволяющие выполнить качественный и количественный анализ элементного состава приповерхностной области твердого тела, среди которых можно выделить: 1) обратное резерфордовское рассеяние (RBS - rutherford backscattering) (Фелдман Л., Майер Д. Основы анализа поверхности и тонких пленок. Пер. с англ. - М.: Мир, 1989. - 344 с.), 2) масс-спектроскопию вторичных ионов (SIMS - secondary ion mass-spectrometry) (Фелдман Л., Майер Д. Основы анализа поверхности и тонких пленок. Пер. с англ. - М.: Мир, 1989. - 344 с.), 3) электронную спектроскопию (Физические основы микроэлектроники / В.И.Марголин, В.А.Жабрев, В.А.Тупик. - М.: Издательский центр «Академия», 2008. - 400 с.).

Способ обратного резерфордовского рассеяния ионов основан на кулоновском взаимодействии заряженной частицы с атомом исследуемого вещества. В результате различия кинематических факторов материалов и вероятностного характера столкновений возможен качественный и количественный элементный концентрационный анализ состава поверхности. Традиционно спектроскопия обратного резерфордовского рассеяния считается неразрушающим методом контроля, на практике необходимо учитывать тот факт, что при бомбардировке поверхности твердого тела может происходить ионное распыление поверхности, образование радиационных дефектов и ионное перемешивание на границе раздела слоев в гетероструктурах. Аппаратное обеспечение рассматриваемого способа сопряжено с необходимостью использования ускорителей ионов, обеспечивающих энергию первичного ионного пучка до 5 МэВ, что ограничивает его широкое применение.

В способе масс-спектроскопии вторичных ионов производится регистрация ионов, образовавшихся из поверхностных атомов при бомбардировке поверхности первичным пучком ионов, при этом разделение ионов происходит по отношению заряда к массе. Разрешение способа по поверхности определяется поперечными размерами зондирующего пучка ионов. Концентрационные профили можно получить, производя послойное стравливание вещества. Анализ элементного состава поверхности можно также осуществлять, определяя элементный состав атомов, распыляемых в нейтральном состоянии, или анализируя излучение атомов, возбуждаемых при распылении. Рассмотренный способ анализа является принципиально разрушающим, так как анализируются атомы, удаляемые с поверхности твердого тела под действием потока первичных ионов.

Наиболее близким по технической сущности к заявляемому способу - прототипом является способ электронной Оже-спектроскопии [A.Jablonski. Quantification of surface-sensitive electron spectroscoies, Surfase Science 603 (2009), P.1342-1352].

Изучаемый образец облучают электронами с энергиями, равными нескольким тысячам электронвольтов. Эти электроны вызывают возбуждение атомов твердого тела, в результате которого возбужденные атомы могут высвобождать свою энергию при излучательных переходах с испусканием кванта электромагнитного (рентгеновского) излучения или при неизлучательных переходах с испусканием электронов. Испускание характеристического рентгеновского излучения является основой рентгеновского микроанализа, а безизлучательный переход с испусканием электронов определенных энергий, соответствующих разности энергетических уровней данного атома, является основой электронной Оже-спектроскопии.

Далее регистрируют Оже-электроны, вышедшие с поверхности твердого тела в вакуум. Энергия Оже-электронов не зависит от энергии первичных электронов и определяется только электронной структурой атомов. Интенсивность потока Оже-электронов I_A в телесный угол ΔΩ при нормальном падении электронов на мишень записывают в виде

где I₀ - интенсивность первичного пучка электронов, σ_i - сечение ионизации уровня первой стадии Оже-процесса, P_A - вероятность выхода данного Оже-электрона, соответствующего ионизации вышеуказанного уровня, r - фактор обратного рассеяния, λ_н - длина пробега относительно неупругого взаимодействия, Y - фактор упругого рассеяния, n - концентрация атомов образца, Р(α) - вероятность поверхностных потерь, α - угол выхода Оже-электронов, отсчитываемый от нормали, ΔΩ - телесный угол, Х - относительная концентрация атомов X-типа [A.Jablonski. Quantification of surface-sensitive electron spectroscoies, Surfase Science 603 (2009), P.1342-1352].

Параметры r, λ_н, Y, M, P определяются составом образца. Приведенное выражение является нелинейным относительно Х (искомой величины) и может быть разрешимо в общем случае только на основе серии допущений. Соответственно, без дополнительных исследований, обеспечивающих определение r, λ_in, Y, P, указанная методика определения элементного состава приповерхностной области твердого тела является лишь качественной. Количественный анализ в настоящее время реализуется при использовании тестовых образцов с известным количественным составом элементов.

Таким образом, основными недостатками прототипа является то, что без дополнительных исследований он обеспечивает лишь качественный элементный анализ образцов, а разрешение по глубине может быть реализовано только в форме разрушающего способа контроля путем последовательного удаления анализируемых слоев с помощью ионного травления.

Задачей заявляемого изобретения является разработка способа определения концентраций элементов, позволяющего получить технический результат, заключающийся в определении концентрации элементов с разрешением по глубине в нанометровом диапазоне без разрушения анализируемого слоя.

Сущность заявляемого изобретения заключается в том, что в способе определения концентрации элементов твердого тела, включающем облучение его поверхности первичным пучком электронов и регистрацию энергетического спектра электронов, вышедших из твердого тела, при известном элементном составе твердого тела последовательно облучают поверхность твердого тела пучком электронов с пошагово увеличивающейся энергией в диапазоне (100-10000) эВ, при каждом значении энергии регистрируют абсолютные значения дифференциального коэффициента упругого отражения электронов в диапазоне углов рассеяния 90-180° при количестве углов, соответствующем количеству элементов в твердом теле, далее рассчитывают средние значения концентраций элементов в зоне выхода и глубину зоны выхода электронов для каждого значения энергии, по которым определяют распределения концентраций элементов по глубине твердого тела.

Определение концентрации элементов приповерхностной области многокомпонентного твердого тела осуществляется за счет того, что в области энергии Е более 100 эВ согласно моделям упругого отражения электронов твердым телом интенсивность упруго отраженных электронов напрямую определяется концентрацией входящих в твердое тело элементов. Определение распределения концентраций элементов по глубине неразрушающим способом осуществляется за счет того, что глубина проникновения и выхода электронов определяется их энергией, и в диапазоне энергий то 100 до 10000 эВ она варьируется от 0,2-0,3 нм до нескольких десятков нм. Таким образом, изменяя энергию электронов, можно неразрушающим способом изменять глубину анализа приповерхностной области твердого тела.

Изобретение поясняют следующие чертежи:

Фиг.1 - Траектория упруго отраженного электрона в использованной модели однократного рассеяния.

Фиг.2 - Траектория упруго отраженного электрона в модели кратного рассеяния.

Фиг.3 - Зависимость дифференциального коэффициента упругого отражения электронов от угла рассеяния в AsS для энергии первичного пучка 1000 эВ (1) и 500 эВ (2).

Способ осуществляют следующим образом.

Образец с известным элементным составом облучают потоком электронов с энергией Е под нормальным углом к поверхности. Измеряют интенсивность потока электронов I(θ_j), отраженных от образца без потери энергии для нескольких углов рассеяния электронов θ_j в диапазоне больших углов рассеяния 150-180° (количество углов рассеяния θ_j должно соответствовать числу k компонентов многокомпонентного исследуемого образца). Значение измеренной интенсивности сопоставляют с теоретически рассчитанной интенсивностью упругого рассеяния I(θ) на угол θ в единичном телесном угле при нормальном угле падения первичных электронов по модели однократного рассеяния (фиг.1) по соотношению:

где I₀ - интенсивность первичного пучка электронов, Р(π-θ) - вероятность поверхностных потерь на угол рассеяния θ, n_i - концентрация i-ого компонента образца, - дифференциальное сечение упругого рассеяния электронов на угол θ для атомов i-ого компонента образца, λ - длина свободного пробега электрона, определяемая из уравнения:

где λ_y, λ_н - длины пробега относительно упругого и неупругого взаимодействия. При этом λ_у в рамках принятой авторами модели определяется из уравнения:

Таким образом, отношение измеренных интенсивностей для различных углов рассеяния θ_j (j пробегает значения от 1 до k) не зависит от λ и дает систему из k-1 уравнений типа:

В системе полученных уравнений неизвестными являются концентрации n_i компонентов образца и вероятности поверхностных потерь.

Для определения вероятности поверхностных потерь Р(θ) в отдельном эксперименте измеряется интенсивность потока упруго отраженных электронов, рассеянных на определенный угол, в зависимости от угла падения φ электронов на поверхность образца. При этом согласно развитой модели отношение интенсивностей определяется выражением:

Аппроксимируя Р выражениями и [A.Jablonski. Quantification of surface-sensitive electron spectroscoies, Surfase Science 603 (2009), P.1342-1352], из уравнения (5) определяем параметр А и соответственно значение Р.

Решая систему уравнений (4), находим отношения атомных концентраций для всех k значений i. Для определения абсолютных концентраций n_i нужно дополнительно измерить плотность образца , где m_i - известная масса атомов i-ого компонента образца.

Подставляя полученные концентрации в уравнение (1) для любого из исследованных углов рассеяния, по экспериментально измеренным I(θ_j) рассчитываем значение длины свободного пробега λ.

Подставляя полученные концентрации в уравнение (3), определяем длину сводного пробега λ_y относительно упругого взаимодействия.

Подставляя значения λ и λ_y в выражение (2), определяем длину сводного пробега λ_н относительно неупругого взаимодействия.

Рассмотренная процедура является первым шагом определения концентраций компонентов мишени, при которой погрешности могут достигать 20%. Для уточнения результатов используется модель кратного рассеяния (фиг.2), согласно которой

где σ_yi - интегральное сечение упругого рассеяния электронов на атомах i-ой компоненты образца, W_z определяет вероятность выхода электронов в вакуум после z-кратного рассеяния и определяется соотношениями:

а λ_y определяется по формуле

S_zi(θ) - нормированная вероятность рассеяния электронов на угол θ при z-кратном рассеянии на атомах i-ой компоненты. Расчет S_zi(θ) проводится на основе следующей процедуры. Нормированные сечения однократного рассеяния S_1i(θ)=(dσ_yi(θ)/dΩ)/σ_yi аппроксимируются с помощью полиномов Лежандра P_l(cosθ) выражением:

где f_il - коэффициенты разложения при полиномах Лежандра. В этом случае, как показано в работе [Мотт Н., Месси Г. Теория атомных столкновений. Пер. с англ. - М.: Мир, 1969. - 756 с.], нормированные сечения z-кратного рассеяния S_iz(θ) могут быть рассчитаны по формуле:

В модели кратного рассеяния электронов отношение интенсивностей упругого рассеяния на углы θ_j определяются по формуле:

Подставляя значения n_i, полученные в модели однократного рассеяния, в уравнение (8) рассчитываем λ_y.

Подставляя полученное таким образом λ_y и рассчитанное в модели однократного рассеяния λ_н в (7), определяем W_z.

Подставляя W_z в систему k-1 уравнений (11) и решая эту систему, определяем уточненные значения отношения концентрации и соответственно уточненные значения концентрации n_i способом, описанным выше.

Подставляя полученные концентрации в уравнение (6), определяем уточненные значения λ.

Подставляя полученные концентрации в уравнение (8), определяем уточненные значения λ_y.

Подставляя полученные значения λ и λ_y в уравнение (2), определяем уточненные значения λ_н.

Полученные таким образом во втором приближении результаты могут быть использованы для последующего уточнения всех определяемых величин по описанной процедуре. Анализ расчетов показывает, что для получения погрешности не более 1% достаточно не более трех циклов.

Рассчитанные таким образом концентрации элементов в приповерхностной области исследуемого объекта представляют собой усредненные значения концентраций компонентов по глубине выхода электронов, определяемой длиной пробега λ, которая в свою очередь определяется энергией первичного электронного пучка.

Для проведения анализа распределения концентраций элементов по глубине необходимо провести описанный цикл для различных энергий Е электронов. При изменении энергии электронов в диапазоне Е=100-1000 эВ толщина анализируемого слоя меняется от долей до единиц нанометров, а в диапазоне Е=1000-10000 эВ - от единиц до десятков нанометров. При больших энергиях сечения упругого рассеяния электронов на атомах слабо меняются с изменением угла рассеяния, и применение рассматриваемого метода требует очень высокой точности измерений дифференциальных коэффициентов упругого отражения электронов.

Процедура получения распределения концентрации элементов по глубине состоит в следующем. Получаемые по описанной методике концентрации элементов являются усредненными по глубине выхода упруго отраженных электронов, которая для больших углов рассеяния θ~150-180° близка к λ. В этом случае экспериментально определяемое значение концентрации соответствует интегралу от профиля концентраций n_i(z).

Варьируя энергию первичного электронного пучка, можно изменять λ и экспериментально определять . Дифференцирование полученной зависимости позволяет рассчитать распределение значений концентраций n_i(z).

В качестве примера рассмотрим процедуру получения профилей концентраций для двухкомпонентного образца As_xS_y.

В модели однократного рассеяния выражение для I(θ) в бинарной системе имеет вид:

где r_θ(θ) - дифференциальный коэффициент упругого отражения. Отношение интенсивностей потоков упруго отраженных электронов в узком телесном угле I(θ₂)/I(θ₁) не зависит от λ и может быть представлено в виде:

Выберем, к примеру, θ₁=160°, θ₂=150°. Из фиг.3 для E=1000 В отношение I(160)/I(150)=r_θ(160)/r_θ(150)=1,18.

Из базы данных ([Powell C.J., Jablonski A. NIST electron elastic-scattering cross-section database. Version 3.1, Standard Reference Data Program Database 64, National Institute of Standards and Technology, Gaithersburg, MD, 2003] получаем:

Экспериментально измеренное отношение для φ=30° и, например, для угла Подставляя это значение в (5), находим параметр поверхностных потерь А=0,095. Подставляя полученные ранее величины в уравнение (14), определяем отношение концентраций . На основании средней плотности образца, равной ρ=3,8 г/см³, определяем абсолютные концентрации n_As=14 нм^-3, n_S=25 нм^-3. Подставляя полученные концентрации в уравнение (13), определяем среднюю глубину выхода электронов λ=1,5 нм. Полученные в первом приближении результаты используем для определения W_z по формулам (7) и (8). Подставляя W_z в уравнение (11) и решая его, определяем отношение и соответственно абсолютные концентрации n_As=16 нм^-3, n_S=23 нм^-3 во втором приближении. Подстановка полученных значений в уравнение (13) позволяет рассчитать λ=1,8 нм. Расчет параметров образца в последующих приближениях дает результаты, практически не отличающиеся от приведенных с точностью ~5%.

Далее процедура повторяется для других энергий электронов. Полученные результаты представлены в таблице 1.

Таблица 1
Рассчитанные значения концентраций и длин свободного пробега
Е, эВ	n(As), 1/нм3	n(S), 1/нм3	λ, нм
250	7	44	0,5
400	7,2	43	0,75
600	10,5	34	1,05
800	12	27	1,4
1000	16	23	1,8
1500	17	22	2,8

Приведенные в таблице 1 концентрации являются усредненными по одновременно определенной глубине выхода λ. Например, для серы (S):

Для определения распределения концентраций элементов n(z) по глубине приповерхностного слоя z необходимо провести процедуру численного дифференцирования выражения (15).

Рассмотрим две глубины выхода λ₁ и λ₂ им соответствуют:

и

В случае малого Δλ=λ₂-λ₁, чему соответствует небольшое отличие энергий, можно приближенно написать

где .

Тогда

Пример расчета концентрации серы на определенной глубине приведен для интервала энергий 800-1000 эВ. Из таблицы для Е=800 эВ значение λ=1,4 нм, а , а для Е=1000 эВ значение λ=1,8 нм, а . Тогда на глубине концентрация серы n_S:

Повторяя описанную процедуру для других интервалов энергий, определяем распределение концентрации серы по глубине приповерхностного слоя. Аналогичная процедура позволяет определить распределение концентрации мышьяка.

В таблице 2 приведены расчеты концентраций мышьяка и серы в исследованном образце.

Таблица 2
Распределение концентраций серы и мышьяка по глубине образца
Z, нм	0,25	0,65	0,9	1,2	1,6
nAs, нм-3	7	9	12	15	15
nS, нм-3	44	36	28	21	21

Способ определения концентрации элементов в приповерхностном слое твердого тела, включающий облучение поверхности твердого тела первичным пучком электронов, регистрацию энергетического спектра электронов, вышедших из твердого тела, отличающийся тем, что при известном элементном составе твердого тела последовательно облучают поверхность твердого тела пучком электронов с пошагово увеличивающейся энергией в диапазоне (100-10000) эВ и при каждом значении энергии регистрируют абсолютные значения дифференциального коэффициента упругого отражения электронов в диапазоне углов рассеяния 90-180° при количестве углов, соответствующем количеству элементов в твердом теле, далее рассчитывают средние значения концентраций элементов в зоне выхода и ее глубину, и на основании этих результатов определяют распределения концентраций элементов по глубине поверхностного слоя твердого тела.