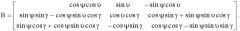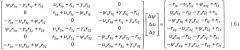Способ спутниковой коррекции гироскопических навигационных систем морских объектов

Способ спутниковой коррекции гироскопических навигационных систем морских объектов

Иллюстрации

Показать все

Реферат

Изобретение относится к средствам коррекции гироскопических навигационных систем и может быть использовано на подвижных объектах, нуждающихся в непрерывном или дискретном определении пространственной ориентации (углы курса ψ, крена γ и дифферента ϑ) глобально, независимо от координат места объекта, времени года и суток, в масштабе реального времени.

В проведении коррекции нуждаются гироскопические системы (инерциальные навигационные системы, гирогоризонткомпасы, компасы и т.п.), способные вырабатывать текущие значения параметров ориентации объекта в автономном режиме функционирования. Необходимость коррекции этих систем вызывается снижением во времени точности выработки ими навигационных параметров в процессе автономного функционирования. Для гирокомпасов характерно также снижение точности определения курса в высоких широтах, в условиях качки и маневрирования корабля.

В настоящее время коррекция курсовых каналов автономных гироскопических систем осуществляется путем выработки поправок курсоуказания с использованием данных пеленгования наземных или космических объектов. В качестве космических объектов используются звезды и спутники спутниковых навигационных систем (СНС).

Для определения курса и углов качки объекта по сигналам среднеорбитных СНС наиболее отработанным в настоящее время является фазовый способ. Этот способ, принимаемый за аналог, базируется на использовании системы разнесенных по объекту приемных антенн, фиксированных относительно его корпуса, измерении разности фаз принимаемых сигналов вычислении углов ориентации объекта.

Для оценки положительных и отрицательных сторон фазового способа рассмотрим следующую ситуацию. Пусть морской подвижный объект с центром масс М перемещается относительно Земли (Фиг.1) по произвольной траектории. В точке М имеют начало горизонтная топоцентрическая координатная система Mξηζ и система координат Mxyz с осями, связанными с объектом. Наряду с поступательным движением, морской объект в условиях качки и маневрирования совершает вращательное движение вокруг точки М.

В рассматриваемом случае положение подвижного объекта в пространстве - ориентация объекта - характеризуется совокупностью параметров ориентации. Применительно к рассматриваемым объектам это могут быть углы горизонтальной (ϑ, γ) и азимутальной (ψ) ориентации объекта.

На Фиг.1 показаны также два навигационных космических аппарата (КА) спутниковой навигационной системы, положение которых в топоцентрической системе координат Mξηζ определено величиной соответствующего вектора визирования и двумя углами - азимутом α и высотой β.

На Фиг.2 показана антенная система из четырех антенн (центральной A₀ и трех разнесенных A_x, А_у, А_z), размещенных на осях ортогонального трехгранника, параллельных осям Mxyz (трехбазовый интерферометр).

Если пренебречь весьма малым в сравнении с дальностью КА отстоянием центральной антенны от центра масс объекта, то в системе Mxyz положение КА можно определять величиной соответствующего вектора визирования и направляющими косинусами cosq_cx, cosq_cy, cosq_cz либо прямоугольными координатами КА, представляющими собой проекции вектора на соответствующие оси: , , . В топоцентрической системе координат положение КА определяется координатами r_cξ, r_cξ, r_cυ. Вся перечисленная информация, характеризующая положение КА, вырабатывается в процессе обсервации по сигналам СНС.

Связь параметров ориентации вектора визирования КА (направляющие косинусы cosq_i) с изменениями разности фаз сигналов СНС определяется выражением

где λ - длина волны сигнала КА;

ℓ_i - база разнесения антенн;

ΔФ_i - разность фаз сигналов, принимаемых на разнесенные антенны;

i=х, у, z.

Реализация фазового способа на морских объектах, однако, сопряжена с определенными трудностями. При определении ориентации объекта по данным фазовых измерений приходится использовать интерферометры с базой, достигающей нескольких метров. В то же время реальные фазоизмерительные устройства имеют диапазон однозначных измерений только в пределах одной длины волны. Это порождает проблему неоднозначности решений при измерении разности фаз сигналов, принимаемых на разнесенные антенны. Кроме того, за счет неидентичности высокочастотных каналов аппаратуры возникают систематические погрешности измерений.

Практическая реализация фазового способа на морских подвижных объектах не дает оснований для излишнего оптимизма. Реализуемая точность коррекции гирокомпасов в высоких широтах часто не удовлетворяет заданным требованиям [1]. Существенными являются и погрешности юстировки протяженных антенных систем на корабле, нежесткость элементов конструкции объекта, многолучевость распространения сигналов и др.

Помимо фазового способа известны другие способы коррекции параметров ориентации с использованием информации СНС.

Известен, в частности, «Гирокомпас с внешней коррекцией» [4], реализующий следующую совокупность приемов, обеспечивающих повышение точности и надежности функционирования в условиях качки и маневрирования корабля:

- принимают сигналы СНС с использованием спутниковой навигационной аппаратуры;

- вычисляют текущие значения широты (φ_c)» северной и восточной составляющих скорости (V_N, V_E);

- формируют сигналы коррекции М_к;

- формируют сигналы управления М_Г, М_В;

- корректируют положение гироскопа гирокомпаса.

Недостатком описанного способа является невозможность измерения и коррекции углов крена и дифферента. Функциональные возможности способа ограничены измерением и коррекцией только курса корабля.

Известна корректируемая система инерциальной навигации и стабилизации ((СИНС) «Ладога-М») [5], принятая за прототип.

В системе реализован классический способ и алгоритм функционирования инерциальной навигационной системы (ИНС) полуаналитического типа с коррекцией по сигналам СНС, а корректирующие сигналы вычисляются с помощью многомерного фильтра калмановского типа.

Уместно отметить, что эффективность процесса оценивания погрешностей курсового канала СИНС существенно зависит от широты расположения объекта. Это ограничивает функциональные возможности корректируемой системы.

На Фиг.3 представлена структура СИНС. В состав системы входят ГП - гироприбор (1), ТС - прибор термостабилизации (2), УМТ - усилитель мощности термостабилизации (3), ПЦ - прибор цифровой (4), ПУ - прибор управления (5), Б-41 - ЭВМ «Багет-41» (6).

Система функционирует следующим образом. Из прибора ГП в прибор ПЦ через аналого-цифровые преобразователи поступают три составляющие ускорения (W_x, W_y, W_z), углы качки и азимутальный угол (Θ_к, ψ_к, А), а из прибора ПЦ в гироприбор ГП подаются управляющие сигналы (Ω_x, Ω_y, Ω_z).

Коррекция СИНС осуществляется путем выработки корректирующей информации (АНД) алгоритмами ЭВМ Б-41 (6) по данным ПЦ (4) НД и приемной аппаратуры СНС, вырабатывающей информацию о координатах Ф_с, λ_с и скорости V_с, ПУ. Управление функционированием СИНС осуществляется по каналам «команды, сигналы».

В систему поступает следующая внешняя информация:

- скорость от лага V_л,

- грубый курс от гирокомпаса К_о,

- координаты φ_с, λ_с, скорость V_c и путевой угол (ПУ) от приемника СНС.

Система имеет два рабочих режима:

- корректируемый режим (КР),

- автономный режим (АР).

В каждом запуске системы производится калибровка системы, которая продолжается от 6 до 8 часов. Калибровка требует поступления внешних позиционных и скоростных данных. Для КР используется информация от приемника СНС и лага, а в АР - только от лага.

Описанной структуре системы соответствует способ, представляющий собой совокупность следующих приемов:

- измеряют три составляющих ускорения (W_x, W_y, W_z);

- принимают данные об углах качки (Θ, ψ) и азимутальном угле (А);

- принимают информацию о координатах (φ_с, λ_с), скорости (V_c) и путевом угле от приемника СНС;

- осуществляют начальную выставку и калибровку системы.

Процесс калибровки состоит в том, чтобы по внешним данным о координатах и скорости СНС вычислить и скорректировать ошибки и воздействия, снижающие точность функционирования СИНС. Поскольку процесс выставки и калибровки продолжается 6-8 часов, оперативная коррекция параметров ориентации изложенным способом не представляется возможной.

Анализ рассмотренных способов определения параметров ориентации объекта позволил выявить также существенное снижение точности определения азимутальной ориентации гиросистемами в высоких широтах и в условиях маневрирования объектов.

Для устранения недостатков аналогов и прототипа в части обеспечения коррекции параметров ориентации объекта предлагается новый способ.

Сущность этого способа следует из связи углов ψ, ϑ, γ с навигационными данными, полученными в процессе обсервации. Такая связь выявляется при рассмотрении выражений для проекций векторов визирования КА на оси трехгранников Mξηζ и Mxyz (Фиг.1; 2). В рассматриваемом случае эти выражения соответствуют матричной зависимости:

где r_cx, r_cy, r_cz - координаты КА в системе Mxyz;

r_cη, r_cζ, r_cξ - координаты КА в системе Mξηζ;

В - преобразующая матрица, соответствующая рассматриваемой геометрии [2].

Выражение (2) однозначно связывает информацию о координатах КА СНС с параметрами ориентации вырабатываемой на объекте гироскопической системой.

Приборные значения углов крена, дифферента и курса можно представить выражениями

где ψ_а, ϑ_а, γ_a - приборные значения углов;

ψ, ϑ, γ - истинные значения углов;

Δψ, Δϑ, Δγ - погрешности выработки углов.

Поскольку углы ψ, ϑ, γ и ψ_а, ϑ_a, γ_a отображают ориентацию истинного и приборного положения трехгранника Mxyz в горизонтной системе осей, их взаимное положение можно описать [3] матрицей направляющих косинусов для случая малого рассогласования координатных систем

где I - единичная матрица;

С учетом формулы (4) выражение (2) принимает вид

где В_A - матрица направляющих косинусов В, содержащая приборные значения углов ориентации.

Таким образом, получена векторно-матричная зависимость (5), однозначно отражающая связь текущих приборных значений углов ψ_а, ϑ_a, γ_a и информации корабельной аппаратуры СНС [r_cη, r_cζ, r_cξ, r_cx, r_cy, r_cz) со значениями погрешностей автономных измерений углов (Δψ, Δϑ, Δγ), подлежащих коррекции.

Учитывая возможность определения ориентации объекта в пространстве по сигналам двух и более КА, можно записать (5) в векторно-матричной форме в виде системы линейных уравнений для неизвестных значений погрешностей автономных средств определения углов

Дальнейшие преобразования позволяют получить расчетные формулы для неизвестных (Δψ, Δϑ, Δγ).

Преобразования уравнений (6) состоят в выполнении следующих действий.

1. Выбор соответствующих пар уравнений системы (6) для первого и второго КА относительно переменных (Δψ, Δϑ), (Δψ, Δγ), (Δϑ, Δγ).

2. Решение каждой пары полученных уравнений для неизвестных Δψ, Δϑ, Δγ.

Для азимутального канала выработки поправки получаем

Для горизонтных каналов выработки корректирующей информации расчетные формулы принимают вид

Анализ расчетных формул поправок к параметрам ориентации позволяет определить объем необходимой для расчета информации. Эта информация включает полный набор текущих приборных значений углов ψ_а, υ_a, γ_a параметров ориентации объекта и значений координат двух навигационных спутников в топоцентрической (r_cη, r_cζ, r_cξ) и cвязанной с объектом (r_сх, r_су, r_сz) системах координат (с=1,2).

В том случае, если на борту морского объекта присутствует аппаратура автономного определения углов качки и курса, а также приемная аппаратура СНС, возможность формирования расчетных формул (7-9) не вызывает сомнения. Расчет текущих значений поправок к текущим значениям параметров ориентации позволяет осуществить коррекцию гироскопических автономных систем и обеспечить решение навигационных задач. Для реализации способа:

- выбирают доступные для обсервации два разнесенных неколлинеарных навигационных спутника (КА);

-принимают данные альманаха и эфемеридной информации приемной аппаратурой объекта-потребителя;

- вычисляют геодезические (географические) координаты потребителя (φ, λ, h);

- вычисляют топоцентрические прямоугольные координаты (r_cξ, r_cη, r_cς) (с=1,2) выбранных КА;

- вычисляют прямоугольные координаты (r_сх, r_су, r_сz) двух выбранных КА в системе координат Mxyz;

- принимают данные гиросистем о текущих значениях параметров ориентации объекта;

- вычисляют поправки к текущим значениям параметров ориентации объекта по данным гиросистемы о текущих значениях параметров ориентации и данным прямоугольных координат КА в топоцентрической и связанной с объектом системах координат;

- корректируют текущие значения параметров ориентации по данным вычисления поправок.

Сущность изобретения поясняется чертежами, где представлены:

Фиг.1. Геометрическая схема;

Фиг.2. Трехбазовый интерферометр;

Фиг.3. Блок схема системы прототипа;

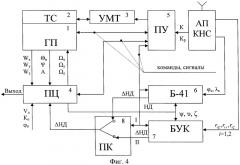
Фиг.4. Блок схема системы, реализующей предлагаемый способ коррекции;

Фиг.5. Графики погрешностей выработки поправок курсоуказания.

Возможность решения задачи коррекции предлагаемым способом позволяет представить структуру интегрированной системы на базе инерциальной системы-прототипа и элементов реализации способа в следующем виде (Фиг.4).

Эта корректируемая система инерциальной навигации и стабилизации содержит гиростабилизированную платформу (1) в трехосном кардановом подвесе с датчиками углов, на которой установлены три двухстепенных интегрирующих гироскопа и три линейных акселерометра. Система также содержит прибор цифровой (4), реализующий алгоритм функционирования инерциальной системы, а также штатный блок коррекции (6). При этом выходы датчиков углов поворота колец карданова подвеса и выхода аксельрометров соединены с входами прибора цифрового, один из выходов которого соединен с входом гиростабилизированной платформы, а другой соединен с блоком коррекции, выход соединяется с прибором цифровым и блоком спутниковой коррекции (8). Выход блока спутниковой коррекции соединен с входами блока коррекции (6) и прибора цифрового (4).

Управление системой осуществляется с пульта (5), обеспечивающего формирование сигналов управления через переключатели ПК в положение II.

Структура корректируемой системы сохраняет основные функциональные элементы и связи системы-прототипа и представляет новый элемент - блок спутниковой коррекции (БСК)(8), связывающий приемную аппаратуру СНС и СИНС.

Взаимодействие блока спутниковой коррекции (8) с элементами СИНС осуществляется в корректируемом режиме (КР) по сигналу от приемной аппаратуры СНС, означающем наличие корректирующей информации. Спутниковая аппаратура вырабатывает информацию о текущих значениях координат места объекта, r_cη, r_cζ, r_cξ, на входы блока коррекции (6) поступают навигационные данные (НД) и спутниковая информация φ_c, λ_c, . Алгоритмы блока (6) вырабатывают оценки погрешностей (дНД I) со скоростью, доступной алгоритмам калмановской фильтрации.

При работе блока (8) осуществляется выработка поправок к автономным значениям параметров ориентации. Сущность процесса выработки поправок состоит в формировании и вычислениях расчетных формул, которые осуществляются в реальном масштабе времени. Текущие значения поправок _ΔНД II поступают через переключатель (ПК)в цифровой блок (4), где происходит коррекция автономных измерений углов ориентации.

Для оценки возможностей рассматриваемого способа проведено математическое моделирование процесса коррекции курса. При этом использована математическая модель СНС ГЛОНАСС в ограниченном составе орбитальной группировки.

На поверхности Земли в плоскости меридиана определены 8 контрольных точек, в которых решается задача определения поправки курсоуказания. В контрольных точках приемная аппаратура принимает сигналы СНС, вырабатывает данные о координатах видимых навигационных спутников и осуществляет выбор спутников. После выбора пары спутников, пригодных для определения ориентации, и приема автономной измерительной информации вычисляются текущие значения поправки курсоуказания.

Результаты моделирования приведены в Таблицах 1 и 2 и представлены в виде графиков на Фиг.5.

Таблица 1 содержит численные значения погрешности определения курса (Δψ=угл. мин) в диапазоне широт (0-80°) на интервале времени (t=50 сек) с шагом Δt=10 сек. Процесс коррекции осуществляется по сигналам двух навигационных спутников, номера которых приведены в таблице. Результаты коррекции представлены численными значениями погрешности определения поправки курса (Δψ угл. мин) с шагом 10 сек.

Таблица 1. Результаты моделирования процесса выработки поправки Δψ.
t, сек	Широта, град	Δψ, мин	Ψ, мин	№ КА1	№ КА2
00	0	-3.027	34.377	3	24
10	0	-3.02	34.377	3	24

t, сек	Широта, град	Δψ, мин	Ψ, мин	№ КА1	№ КА2
20	0	-3.013	34.377	3	24
30	0	-3.006	34.377	3	24
40	0	-2.998	34.377	3	24
50	0	-2.991	34.377	3	24
00	10	0.034	34.377	3	22
10	10	0.033	34.377	3	22
20	10	0.032	34.377	3	22
30	10	0.031	34.377	3	22
40	10	0.031	34.377	3	22
50	10	0.030	34.377	3	22
00	20	-0.117	34.377	3	22
10	20	-0.118	34.377	3	22
20	20	-0.119	34.377	3	22
30	20	-0.119	34.377	3	22
40	20	-0.12	34.377	3	22
50	20	-0.12	34.377	3	22
00	30	-0.232	34.377	3	22
10	30	-0.232	34.377	3	22
20	30	-0.233	34.377	3	22
30	30	-0.233	34.377	3	22
40	30	-0.234	34.377	3	22
50	30	-0.234	34.377	3	22
00	40	-1.192	34.377	3	20
10	40	-1.188	34.377	3	20
20	40	-1.184	34.377	3	20
30	40	-1.18	34.377	3	20
40	40	-1.176	34.377	3	20
50	40	-1.172	34.377	3	20
00	50	0.396	34.377	1	20
10	50	0.394	34.377	1	20
20	50	0.393	34.377	1	20
30	50	0.392	34.377	1	20
40	50	0.390	34.377	1	20
50	50	0.389	34.377	1	20
00	60	-0.044	34.377	4	22
10	60	-0.043	34.377	4	22
20	60	-0.042	34.377	4	22
30	60	-0.041	34.377	4	22
40	60	-0.04	34.377	4	22
50	60	-0.039	34.377	4	22
00	70	-0.165	34.377	4	21
10	70	-0.164	34.377	4	21
20	70	-0.164	34.377	4	21
30	70	-0.163	34.377	4	21
40	70	-0.163	34.377	4	21
50	70	-0.162	34.377	4	21
00	80	-0.266	34.377	4	21
10	80	-0.265	34.377	4	21
20	80	-0.265	34.377	4	21

t, с	Широта, град	Δψ, мин	Ψ, мин	№ КА1	№ КА2
30	80	-0.264	34.377	4	21
40	80	-0.264	34.377	4	21
50	80	-0.263	34.377	4	21

На Фиг.5 представлены графики погрешности выработки поправок курсоуказания Δψ в зависимости от широты места объекта и номера используемых навигационных спутников.

Характер изменения графиков погрешностей свидетельствует о высокой точности выработки поправок курса по данным СНС. Во всем диапазоне изменения широты объекта (φ=0-80°) погрешность Δψ не превышает - 3÷+4 угловых минут. Полностью отсутствует зависимость точности от широты места объекта. В то же время очевидна связь погрешности и взаимного расположения навигационных спутников и объекта. Решение задачи осуществляется в реальном масштабе времени.

В таблице 2 представлены результаты моделирования влияния погрешности начальной выставки гироскопической системы на точность выработки поправки курса.

Из таблицы 2 следует возможность повышения точности определения поправок ориентации в широком диапазоне погрешностей гироскопической системы.

Помимо выработки поправки курса подобным образом осуществляется по формулам (8), (9) выработка поправок к углам горизонтальной ориентации.

По результатам проведенных исследований можно сделать вывод о высокой эффективности предложенного способа коррекции параметров ориентации объекта. В результате реализации предлагаемого способа достигаются следующие преимущества:

- обеспечивается непрерывная коррекция углов ориентации объекта вырабатываемых гиросистемой;

- коррекция осуществляется в реальном времени функционирования системы;

- коррекция обеспечивается в любом районе мирового океана с точностью, не зависимой от широты места объекта;

- надежность функционирования и высокая точность навигационных определений обеспечивается строгим контролем текущего состояния всех элементов СНС.

Таблица 2. Результаты моделирования процесса выработки поправки.
t, с	φ, град.	Ψ1, мин	δΨ1, мин	ΔΨ1, мин	Ψ2, мин	δΨ2, мин	ΔΨ2, мин	Ψ3, мин	δΨ3, мин	ΔΨ3, мин	Ψ4, мин	δΨ4, мин	ΔΨ4, мин	№КА
1	2
4800	0	0	0	0	17.189	17.963	-0.775	34.377	37.404	-3.027	68.755	80.334	-11.579	3	24
4810	0	0	0	0	17.189	17.961	-0.773	34.377	37.397	-3.02	68.755	80.311	-11.556	3	24
4820	0	0	0	0	17.189	17.959	-0.771	34.377	37.39	-3.013	68.755	80.287	-11.532	3	24
4800	10	0	0	0	17.189	17.181	0.008	34.377	34.344	0.034	68.755	68.592	0.163	3	22
4810	10	0	0	0	17.189	17.181	0.007	34.377	34.344	0.033	68.755	68.595	0.16	3	22
4820	10	0	0	0	17.189	17.182	0.007	34.377	34.345	0.032	68.755	68.599	0.156	3	22
4800	20	0	0	0	17.189	17.218	-0.03	34.377	34.495	-0.117	68.755	69.214	-0.459	3	22
4810	20	0	0	0	17.189	17.219	-0.03	34.377	34.495	-0.118	68.755	69.216	-0.461	3	22
4820	20	0	0	0	17.189	17.219	-0.03	34.377	34.496	-0.119	68.755	69.218	-0.463	3	22
4800	30	0	0	0	17.189	17.247	-0.058	34.377	34.61	-0.232	68.755	69.68	-0.925	3	22
4810	30	0	0	0	17.189	17.247	-0.058	34.377	34.61	-0.232	68.755	69.682	-0.927	3	22
4820	30	0	0	0	17.189	17.247	-0.058	34.377	34.61	-0.233	68.755	69.683	-0.928	3	22
4800	40	0	0	0	17.189	17.485	-0.296	34.377	35.569	-1.192	68.755	73.59	-4.835	3	20
4810	40	0	0	0	17.189	17.484	-0.295	34.377	35.565	-1.188	68.755	73.574	-4.819	3	20
4820	40	0	0	0	17.189	17.483	-0.294	34.377	35.561	-1.184	68.755	73.558	-4.803	3	20
4800	50	0	0	0	17.189	16.241	0.948	34.377	30.42	3.958	68.755	51.444	17.311	1	20
4810	50	0	0	0	17.189	16.244	0.945	34.377	30.433	3.944	68.755	51.505	17.25	1	20
4820	50	0	0	0	17.189	16.247	0.942	34.377	30.447	3.93	68.755	51.565	17.189	1	20
4800	60	0	0	0	17.189	17.200	-0.011	34.377	34.421	-0.044	68.755	68.912	-0.157	4	22
4810	60	0	0	0	17.189	17.200	-0.011	34.377	34.42	-0.043	68.755	68.908	-0.153	4	22
4820	60	0	0	0	17.189	17.200	-0.011	34.377	34.419	-0.042	68.755	68.904	-0.149	4	22
4800	70	0	0	0	17.189	17.230	-0.041	34.377	34.542	-0.165	68.755	69.407	-0.652	4	21
4810	70	0	0	0	17.189	17.230	-0.041	34.377	34.542	-0.164	68.755	69.405	-0.65	4	21
4820	70	0	0	0	17.189	17.230	-0.041	34.377	34.541	-0.164	68.755	69.403	-0.648	4	21
4800	80	0	0	0	17.189	17.255	-0.066	34377	34.643	-0.266	68.755	69.816	-1.061	4	21
4810	80	0	0	0	17.189	17.255	-0.066	34377	34.643	-0.265	68.755	69.814	-1.059	4	21

ЛИТЕРАТУРА

1. Андреев А.А., Кокорин В.И. и др. Результаты высокоширотных испытаний современных российских морских компасов. Труды международной конференции по интегрированным навигационным системам- СПб.: ЦНИИ «Электроприбор», 2004. с.137-139.

2. Ривкин С.С.Статистический синтез гироскопических устройств. - Л.: Судостроение, 1970.

3. Броксмейер Ч.Ф. Системы инерциальной навигации. - Л.: Судостроение, 1967.

4. Резниченко В.И. Гирокомпас с внешней коррекцией. - М.: Официальный бюллетень изобретений №19, 1996.

5. Пешехонов В.Г. и др. Единая система инерциальной навигации и стабилизации «Ладога-М». Морская радиоэлектроника №1(4), 2003. с.26-30.

Способ спутниковой коррекции гироскопических навигационных систем по данным автономных измерений этих систем и по сигналам спутниковой навигационной системы, включающий выбор навигационных спутников, прием навигационной и служебной информации, вычисление координат места объекта, вычисление поправок к приборным значениям параметров ориентации и коррекцию параметров ориентации, отличающийся тем, что принимают данные гиросистемы о текущих значениях параметров ориентации объекта; выбирают два неколлинеарных навигационных спутника; вычисляют топоцентрические прямоугольные координаты выбранных спутников; вычисляют прямоугольные координаты выбранных спутников в связанной с объектом системе координат; вычисляют поправки к текущим значениям параметров ориентации объекта гиросистемы по данным о текущих значениях параметров ориентации и прямоугольных координат спутников в топоцентрической и связанной с объектом системах координат; корректируют текущие значения параметров ориентации гиросистемы по данным вычисленных поправок.