Способ кодирования оцифрованных изображений с использованием дискретного вейвлет-преобразования адаптивно определенного базиса

Способ кодирования оцифрованных изображений с использованием дискретного вейвлет-преобразования адаптивно определенного базиса

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к области сжатия изображений. Изобретение может быть использовано в системах передачи и хранения видеоданных и изображений. Более конкретно, рассматриваются схемы кодирования изображений, использующие субполосное преобразование изображения с последующим энтропийным кодированием. Субполосное преобразование детально рассмотрено в работе [Теория и практика вейвлет-преобразования. Воробьев В.И., Грибунин В.Г. ВУС, 1999].

Многие из распространенных видеосистем используют различные способы кодирования, которые необходимы для сокращения времени передачи данных по каналам связи и сокращения объемов носителей для записи данных.

С появлением видеосистем высокого разрешения потребность в цифровом кодировании изображений возросла. Были достигнуты такие коэффициенты сжатия, при которых стало возможным построение систем телевидения высокого разрешения, в том числе и беспроводных.

Многие стандартные алгоритмы компрессии изображений (например, JPEG) и видеоданных (например, MPEG-1, 2, 4, Н.263 и Н.264) используют дискретное косинусное преобразование (ДКП). Это обусловлено тем фактом, что ДКП, которое может быть реализовано на основе алгоритма быстрого преобразования Фурье (БПФ), достаточно хорошо аппроксимирует преобразование Карунена-Лоэва, которое дает полную декорреляцию гауссова сигнала и не имеет быстрого алгоритма расчета. Одновременно с этим даже для быстрых алгоритмов расчета ДКП наблюдается практически экспоненциальная зависимость объема вычислений от размера обрабатываемых изображений, что, в том числе, приводит к необходимости обрабатывать изображение не целиком, а поблочно: изображение разбивается на блоки, которые преобразуются с использованием ДКП. Как правило, блоки имеют размеры 8×8, 16×16, 32×32, 64×64 пикселов. В частности, в широко известном алгоритме JPEG используются блоки размером 8×8. Такой подход приводит к весьма существенному недостатку - возникновению артефакта блочности, то есть к наличию видимых границ между блоками пикселей на декодированных изображениях, что существенно ухудшает их субъективное восприятие. Более подробно об использовании ДКП для сжатия изображений можно узнать из стандарта ISO/IEC 10918-1: 1993.

Другая схема основывается на субполосном преобразовании изображения с последующим устранением межполосной избыточности при помощи древовидных структур. Фундаментальной работой, в которой описывается эта схема, можно считать [A.Said, W.Pearlman. Image Compression Using the Spatial-Orientation Tree. IEEE Int. Symp. On Circuits and Systems, Vol.1, pp.279-282, May 1993].

Используя субполосное преобразование, изображение преобразуется в набор субполос, каждая из которых представляет собой матрицу коэффициентов преобразования. В качестве субполосного преобразования наиболее широкое применение нашел способ вейвлет-разложения по схеме Малла. В этом случае используется реализация вейвлет-преобразования в виде квадратурного зеркального фильтра с ядром, вид которого определяется используемым вейвлет-базисом. Подробное описание этой схемы можно найти в работе "A theory for multiresolution signal decomposition: the wavelet representation", IEEE Transaction on Pattern Analysis and Machine Intelligence, vol.11, p.674-693, July 1989.

После субполосного преобразования используется совместное кодирование субполос. Цель такого кодирования - получение последовательности бит (битового потока), пригодной для восстановления субполос. Особенностью совместного кодирования субполос является возможность использования начальной части произвольного размера от полученного потока. Чем больше размер используемой для восстановления части битового потока, тем меньше расхождение коэффициентов преобразования восстановленных субполос с кодируемыми. Это свойство битового потока достигается за счет определенной очередности кодирования коэффициентов преобразования кодируемых матриц. Коэффициенты преобразования с большим абсолютным значением начинают кодироваться раньше, чем коэффициенты преобразования с меньшим значением. Устранение межполосной избыточности достигается с помощью объединения коэффициентов преобразования разных субполос и их кодирования с помощью иерархического дерева. Подобные способы описаны в патентах США №№5764807, 5216423, 5321776, а также в работе J. Shapiro "Embedded image coding using zero tree of wavelet coefficients", IEEE Trans. On Signal Processing, vol.41, pp.3445-3462, Dec. 1993.

Цель предлагаемого изобретения - сокращение объема передаваемых или сохраняемых данных по сравнению с исходными данными.

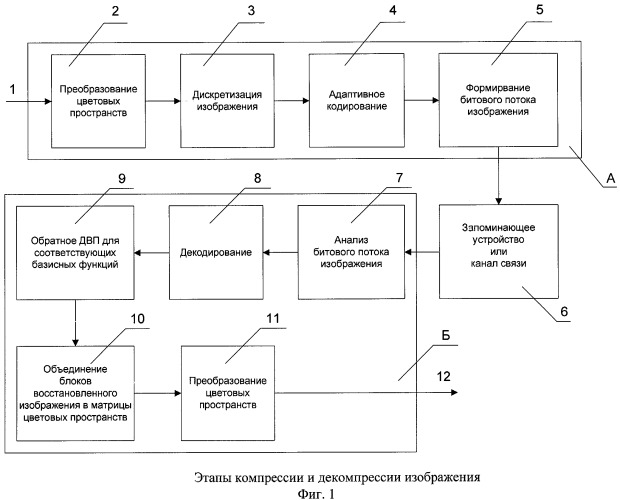
Компрессия А и декомпрессия Б изображения представлена на фиг.1. Входное изображение 1 подвергается преобразованию цветовых пространств на этапе 2, результатом которого являются матрицы пикселов, соответствующие цветовым пространствам изображения (например, матрица яркости, матрица контрастности и матрица цветности). Каждая из этих матриц передается на этап 3 дискретизации изображения, на котором происходит его сегментация и образуются блоки исходного изображения (далее по тексту - БИИ). Затем производится этап 4 адаптивного кодирования с использованием методов статистического, корреляционного и спектрального анализа: происходит адаптивное определение вейвлет-базисов для БИИ, выполняется дискретное вейвлет-преобразование (далее по тексту - ДВП), а также происходит выполнение других действий по кодированию БИИ. Способ определения вейвлет-базиса может быть как одним для всех БИИ, так и различаться от блока к блоку. Кроме того, при расчете коэффициентов ДВП субполос БИИ, для каждой из этих субполос может быть использован свой вейвлет-базис. Завершающим этапом 5 является формирование битового потока изображения. Полученные последовательности бит для каждого из БИИ дополняются служебной информацией (например, информацией о размерах блоков, размерах изображения, используемых вейвлет-базисах и т.д.) и объединяются в битовый поток изображения. Окончание этапа 5 означает завершение компрессии А входного изображения 1 и результирующая битовая последовательность на этапе 6 может быть записана запоминающим устройством, или передана по каналу связи.

При необходимости восстановления изображения, записанная или переданная последовательность бит подвергается декомпрессии Б. На этапе 7 декомпрессии Б происходит анализ битового потока изображения, извлечение служебной информации и выделение последовательностей бит, соответствующих кодированным коэффициентам ДВП для БИИ. Полученная служебная информация и последовательности бит позволяют осуществить декодирование на этапе 8 и обратное ДВП для соответствующих базисных функиций на этапе 9 для того, чтобы в результате получить блоки восстановленного изображения. Полученные на этапе 9 блоки восстановленного изображения в соответствии со служебной информацией на этапе 10 объединяются в матрицы цветовых пространств восстановленного изображения. После того, как все матрицы изображения восстановлены, наступает этап преобразования цветовых пространств 11, представляющий собой восстановленное изображение в виде матриц требуемого цветового пространства. Результатом декомпрессии Б является восстановленное изображение 12.

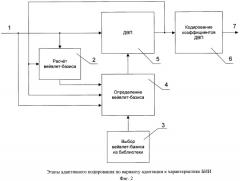
Фиг.2 иллюстрирует этапы адаптивного кодирования по варианту адаптации посредством характеристики БИИ. На фиг.2 БИИ 1 используется для расчета вейвлет-базиса на этапе 2. Расчет вейвлет-базиса можно осуществить так, как это показано в работе [R.R.Coifman and M.V.Wickerhauser. Entropy-based algorithms for best basis selection. IEEE Trans. Information Theory, 38: 1241-1243, March 1992]. На этапе 3 происходит выбор вейвлет-базиса из библиотеки. На этапе 4 происходит определение вейвлет-базиса путем расчета характеристики БИИ с использованием результатов этапов 2 и 3. Для получения характеристики БИИ может использоваться оценка степени корреляции с пикселями БИИ, например, взаимная корреляционная функция между вейвлет-базисом и подмножеством пикселов, находящихся в одной строке или в одном столбце блока. Пусть дан блок исходного изображения Х размером (М×N) пикселов. Возможно выделить подмножества пикселов X_i, принадлежащие блоку Х. Тогда для заданного набора базисов W возможно найти множество оценок F_i (X_i, W), в качестве которых могут использоваться сумма значений или максимум значений

- взаимной корреляционной функции между одномерным вейвлет-базисом и одномерными подмножествами X_i блока Х (в частности, такими одномерными подмножествами являются строки и столбцы блока Х);

- двумерной взаимной корреляционной функции между двумерным вейвлет-базисом W и двумерными подмножествами X_i блока Х (в частности, такими двумерными подмножествами являются блоки пикселов размерами (m_i×n_i), принадлежащие блоку Х, т.е. m_i≤М, n_i≤N).

Для получения характеристики БИИ H(W) следующее соотношение:

Вейвлет-базис W, для которого обеспечивается максимум значения характеристики H(W), используется при осуществлении очередной итерации этапа ДВП 5. В качестве исходных данных для первой итерации ДВП используется БИИ, а для каждой из последующих итераций - коэффициенты ДВП, полученные на предыдущей итерации. Для каждой итерации может быть определен свой вейвлет-базис путем повторения этапов 2 и 4. При этом исходные данные Х для этих этапов такие же, как и для текущей итерации ДВП. После расчета всех коэффициентов ДВП, они подвергаются кодированию на этапе 6, результатом которого является последовательность бит 7.

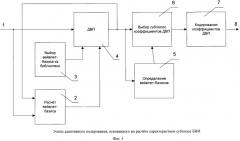
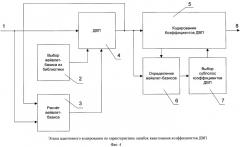
Существует и другой способ адаптивного кодирования, основанный на расчете характеристики субполос БИИ. В этом случае этапы адаптации представлены на фиг.3. Входными данными является БИИ 1. На этапах 2 и 3 формируется набор вейвлет-базисов, для каждого элемента которого выполняется итерация ДВП на этапе 4. Исходные данные для расчета вейвлет-базиса на этапе 2 совпадают с исходными данными текущей итерации ДВП. В результате выполнения каждой итерации этапа 4 для набора вейвлет-базисов получается набор субполос коэффициентов ДВП, определение вейвлет-базиса на этапе 5 осуществляется с помощью характеристики субполос БИИ, рассчитываемой по формуле:

где S - множество субполос БИИ, выбранных для расчета оценки F; f - неубывающая функция.

Оценка F рассчитывается как неубывающая функция от суммы абсолютных значений коэффициентов ДВП, возведенных в некоторую степень и принадлежащих одной из субполос множества S. На этапе 6 производится выбор субполос коэффициентов ДВП, причем выбираются те субполосы, которые были получены с помощью вейвлет-базиса W, для которого обеспечивается минимум значения характеристики H(W). Коэффициенты ДВП, принадлежащие выбранным на этапе 6 субполосам, подвергаются кодированию 7, результатом которого является последовательность бит 8.

Множество S также может быть получено и после этапа квантования, который является составной частью этапа кодирования. В этом случае используется адаптивное кодирование по характеристике ошибок квантования коэффициентов ДВП. Этапы для этого случая рассмотрены на фиг.4. БИИ 1 и этапы 2, 3, 4 повторяются в соответствии с БИИ 1 и этапами 2, 3, 4 фиг.3. При кодировании коэффициентов ДВП на этапе 5 квантованные значения коэффициентов ДВП передаются на этап 6, на котором происходит определение вейвлет-базисов путем расчета характеристик ошибок квантования по формуле (2). В этом случае F рассчитывается как неубывающая функция от суммы абсолютных значений ошибок квантования коэффициентов ДВП, возведенных в некоторую степень и принадлежащих одной из субполос множества. На этапе 7 происходит выбор субполос коэффициентов ДВП, причем выбираются те субполосы, которые были получены с помощью вейвлет-базиса W, для которого обеспечивается минимум значения характеристики H(W). Оставшиеся на этапе 5 действия по кодированию коэффициентов ДВП выполняются не для всего набора субполос коэффициентов ДВП, а только для тех субполос, которые были выбраны на этапе 7. Результатом этапа 5 является последовательность бит 8.

Другой вариант адаптации основан на оценке ошибки восстановления блоков изображения. Адаптивное кодирование по данному варианту представлено на фиг.5. БИИ 1 и этапы 2, 3, 4 полностью повторяют этапы предыдущего способа. На этапе 5 осуществляется кодирование всех субполос коэффициентов ДВП для каждого вейвлет-базиса заданного набора. Полученные в результате последовательности бит выравниваются по длине путем отбрасывания некоторого количества бит от их окончания. На этапе 6 эти битовые последовательности восстанавливаются в блоки с использованием тех вейвлет-базисов, которые применялись для ДВП перед их кодированием. Восстановленные блоки и БИИ 1 участвуют в расчете ошибок восстановления блоков изображения. Определение вейвлет-базисов на этапе 7 осуществляется по формуле:

где - пиксел восстановленного блока изображения, причем при кодировании последовательности бит и ее декодировании применялся вейвлет-базис W; x_i,j - пиксел БИИ; f - неубывающая функция.

На этапе 8 выбирается такая последовательность бит, для которой будет минимальным абсолютное значение H(W), полученное на этапе 7. Результатом этапа 8 является последовательность бит 9.

1. Способ кодирования оцифрованных изображений, содержащий следующие этапы: дискретизация изображения; адаптивное кодирование; формирование битового потока, и отличающийся тем, что исходное изображение разбивается на блоки, и для упомянутых блоков выполняется дискретное вейвлет-преобразование с использованием вейвлет-базисов, которые были определены адаптивно на этапе адаптивного кодирования.

2. Способ по п.1, отличающийся тем, что определение вейвлет-базиса производится на основе значений характеристик, полученных для блока исходного изображения методами статистического, корреляционного и спектрального анализа.

3. Способ по п.2, отличающийся тем, что для дискретного вейвлет-преобразования выбирается такой вейвлет-базис, для которого оценка степени корреляции со значениями пикселей блока исходного изображения максимальна.

4. Способ по п.3, отличающийся тем, что для определения степени корреляции между вейвлет-базисом и значениями пикселов блока исходного изображения используется взаимная корреляционная функция.

5. Способ по п.3, отличающийся тем, что при определении оценки степени корреляции между вейвлет-базисом и значениями пикселей блока исходного изображения используются подмножества пикселей, находящихся в одной строке или в одном столбце, принадлежащих блоку.

6. Способ по п.1, отличающийся тем, что определение вейвлет-базиса производится после дискретного вейвлет-преобразования над блоками исходного изображения на основе значений характеристик, полученных для субполос этих блоков методами статистического, корреляционного и спектрального анализа.

7. Способ по п.6, отличающийся тем, что в качестве характеристики для определения вейвлет-базиса для выполнения дискретного вейвлет-преобразования над блоком исходного изображения используется неубывающая функция от суммы абсолютных значений коэффициентов дискретного вейвлет-преобразования, возведенных в некоторую степень и принадлежащих заранее выбранным субполосам блока.

8. Способ по п.7, отличающийся тем, что для дискретного вейвлет-преобразования выбирается вейвлет-базис, который обеспечивает минимальное значение неубывающей функции от суммы абсолютных значений коэффициентов дискретного вейвлет-преобразования, возведенных в некоторую степень и принадлежащих заранее выбранным субполосам блока исходного изображения.

9. Способ по п.7 или 8, отличающийся тем, что для расчета значения неубывающей функции от суммы абсолютных значений коэффициентов дискретного вейвлет-преобразования, возведенных в некоторую степень, выбираются коэффициенты дискретного вейвлет-преобразования, принадлежащие не всем субполосам блоков, а только их части.

10. Способ по п.1, отличающийся тем, что для дискретного вейвлет-преобразования над блоком исходного изображения выбирается такой вейвлет-базис, для которого значение функции ошибки восстановления блока изображения будет минимальным.

11. Способ по п.10, отличающийся тем, что функция ошибки восстановления определяется как неубывающая функция от суммы абсолютных значений ошибок квантования коэффициентов преобразования, возведенных в некоторую степень и принадлежащих субполосам блока исходного изображения, подвергаемых квантованию.

12. Способ по п.10, отличающийся тем, что функция ошибки восстановления блока изображения определяется как неубывающая функция от суммы абсолютных значений, возведенных в некоторую степень и рассчитываемых как отклонения пикселей восстановленного блока изображения от пикселей исходного блока изображения.