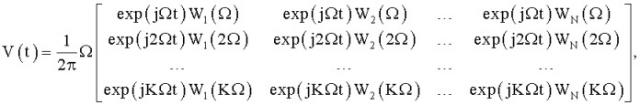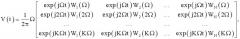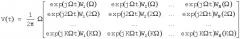Способ спектрального анализа электрического сигнала

Способ спектрального анализа электрического сигнала

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиоэлектроники, а именно - к спектральному анализу электрических сигналов.

Одной из главных задач спектрального анализа электрических сигналов (далее - спектрального анализа) является повышение точности и разрешающей способности анализаторов спектров электрических сигналов, особенно в радиодиапазоне, где осуществляется основной объем телекоммуникаций. Существуют различные подходы к решению этих задач.

Известны способы спектрального анализа, обеспечивающие высокие точность и разрешение, основанные на цифровой обработке автокорреляционной функции анализируемого сигнала

,

где x(t) - анализируемый сигнал, М{·} обозначает математическое ожидание.

Одним из таких способов является авторегрессионное оценивание энергетического спектра сигнала [1]. Способ заключается в том, что определяют по измерениям сигнала значения его автокорреляционной функции в дискретные моменты времени ρ(0), ρ(Δt), …ρ(nΔt), где Δt - шаг дискретизации по времени, затем используют эти значения в уравнении Юла-Уокера и находят из него коэффициенты авторегрессионной модели, которые позволяют реккурентным образом определять значения автокорреляционной функции ρ(τ) со значениями τ=(n+1)Δt, (n+2)Δt, ..., увеличивая, таким образом, число отсчетов коррелляционной функции. Эти новые отсчеты вместе с измеренными используют для расчета энергетического спектра анализируемого сигнала, который определяется как преобразование Фурье от автокорреляционной функции:

где j - комплексная единица, а ω - круговая частота.

Чем большее число отсчетов автокорреляционной функции учтено в сумме в правой части этого выражения, тем точнее будет результат - энергетический спектр P(ω) и выше разрешение. Таким образом, за счет рекуррентного определения значений автокорреляционной функции появляется возможность получить высокое разрешение при ограниченном числе начальных замеров корреляционной функции.

Недостатки авторегрессионного способа, как и других способов спектрального анализа, основанных на обработке автокорреляционной функции анализируемого сигнала, следующие.

1. Необходимость предварительного определения дискретных значений автокорреляционной функции сигнала. Это требует не только определенных временных затрат, но и специальной аппаратуры.

2. Невозможность на основе обработки автокорреляционной функции определять фазовый спектр сигнала, а лишь его энергетический спектр и связанный с ним простым соотношением амплитудный спектр.

3. Поскольку методы спектрального анализа на основе обработки автокорреляционной функции - вычислительные, т.е. цифровые, измеряемые величины должны быть оцифрованы с использованием аналого-цифровых преобразователей (АЦП). Так, экспериментальные оценки автокорреляционной функции обычно определяют, усредненяя дискретные значения самого сигнала, измеренные в соответствующие моменты времени:

где τ=0, Δt, 2Δt, …, означает экспериментальную оценку, N - число замеров. Из-за ограниченного быстродействия АЦП такие измерения позволяют анализировать спектры лишь относительно низкочастотных сигналов, например гидроакустических. Однако для анализа спектров в радиодиапазоне основанная на подобных цифровых измерениях обработка не применима.

Для спектрального анализа в радиодиапазоне применяют способы, основанные на использовании фильтров. Известен способ одновременного спектрального анализа [2] (прототип предлагаемого способа), который состоит в том, что анализируемый сигнал подается одновременно на гребенку резонаторов, настроенных на различные частоты, и на выходах резонаторов измеряют сигналы, пропорциональные составляющим амплитудного спектра сигнала на частотах настройки (собственных частотах) резонаторов.

Этот способ-прототип, хотя и позволяет, в отличие от аналогов, анализировать сигналы радио диапазона, однако обладает следующими недостатками.

1. Для достижения высоких точности и разрешения спектрального анализа в прототипе необхоимо увеличивать число фильров-резонаторов и уменьшать их затухание. Однако высокодобротные резонаторы обладают большим временем переходных процессов, что замедляет проведение спектрального анализа [2, стр.109]. Таким образом, высокие точность и разрешение достигаются как аппаратурными, так и временными дополнительными затратами.

2. Прототип не позволяет определять фазовый спектр, а определяет лишь амплитудный спектр сигнала.

Технической задачей данного изобретения является создание способа спектрального анализа, основанного на применении фильтров-резонаторов, но позволяющего достигать повышенных точности и разрешения без увеличения числа резонаторов и их добротности, а также анализировать комплексный спектр сигнала, включая его фазовую составляющую.

Поставленная задача достигается тем, что в способе спектрального анализа, заключающемся в том, что анализируемый электрический сигнал подается одновременно на гребенку фильтров-резонаторов, настроенных на различные частоты, и измеряются сигналы на выходах этих фильтров, согласно изобретению, до проведения измерений диапазон контролируемых частот разбивают на элементы разрешения с шагом дискретизации Ω, соответствущим желаемым точности и разрешению спектрального анализа и существенно меньшим полосы пропускания используемых фильтров, определяют дискретные значения комплексной передаточной функции каждого фильтра во всех элементах разрешения W_i(Ω), W_i(2Ω), … (W_i(KΩ), где i - номер фильтра, K - число элементов разрешения в диапазоне контролируемых частот, формируют матрицу

где N - число фильтров, а j - комплексная единица, в некоторый момент времени t фиксируют значения сигналов на выходах всех фильтров и объединяют их в вектор где - сигнал на выходе i-го фильтра в момент времени t, Т означает транспонирование, определяют искомый комплексный спектр анализируемого сигнала в дискретизированном виде с шагом дискретизации Ω, решая относительно вектора s векторно-матричное уравнение , где S(kΩ) - значение комплексного спектра анализируемого сигнала, приходящееся на k-й элемент разрешения, при этом решение находят одним из методов линейной алгебры, например методом псевдообращения , где + обозначает операцию псевдообращения матрицы, - оценка вектора s, или, при необходимости, учитывать ошибки измерений, оценку вектора s находят методом оценивания из уравнения измерений , где n - вектор ошибок измерений сигналов на выходах фильтров.

Положительный эффект достигается за счет нового принципа спектрального анализа, основанного на использовании заранее определенных дискретных значений характеристик фильтров и проведении одновременной фиксации значений сигналов на выходах всех фильтров. Причем шаг дискретизации характеристик фильтров определяет точность и разрешение спектрального анализа.

Особенностью предлагаемого способа является то, что в нем оценивается значение составляющих комплексного спектра анализируемого сигнала в каждом элементе разрешения. Учитывая, что размер элемента разрешения гораздо меньше полосы пропускания используемых фильтров, это обеспечивает значительное повышение разрешения и точности спектрального анализа по сравнению с прототипом, причем без увеличения числа фильтров и/или их добротности, а также без предварительного определения автокорреляционной матрицы принимаемого сигнала, как это делается в известных аналогах высокоточного спектрального анализа. Поскольку требования к добротности в заявляемом способе минимальные, это позволяет достигать также повышенного быстродействия при спектральном анализе. Существенным свойством заявляемого способа является и то, что он позволяет анализировать комплексный спектр сигнала, включая его фазовую составляющую.

Обоснование способа.

Пусть анализируемый сигнал описывается функцией времени x(t). Спектральная плотность, или комплексный спектр этого сигнала, определяется его преобразованием Фурье

где ω - круговая частота.

Задача заключается в определении комплексного спектра S(ω) с высокой точностью и разрешением по частоте. Заметим при этом, что S(ω) - комплексная величина, которая разделяется на амплитудный спектр и фазовый спектр. Способ-прототип позволяет анализировать только амплитудный спектр, а заявляемый способ - полный комплексный спектр S(ω).

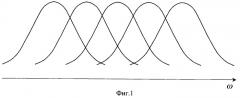
Для спектрального анализа используем гребенку перекрывающихся по частоте фильтров (фиг.1), представляющих собой резонаторы с полосой пропускания, существенно превышающей желаемые точность и разрешение спектрального анализа. На эти фильтры одновременно будем подавать анализируемый сигнал x(t). В прототипе для повышения разрешающей способности и точности спектрального анализа необходимо увеличивать добротность резонаторов и их число. Делать это технически трудно. В заявляемом способе используем новый принцип спектрального анализа, позволяющий достигать повышения точности и разрешающей способности спектрального анализа без увеличения добротности и числа фильтров.

Пусть i-й фильтр имеет передаточную функцию W_i(jω). Эта функция комплексная, характеризующая распределение по частотам усилений и фазовых сдвигов фильтра. Далее будем обозначать эту функцию W_i(ω), что в большей степени соответствует ее конкретным выражениям. Так, передаточная функция резонатора имеет вид [3]

где ω₀ - собственная частота резонатора, α - коэффициент затухания.

Входящие в уравнение (1) постоянные величины ω₀ и α определяются параметрами схемы резонатора. Для резонатора в виде одиночного контура, состоящего из катушки индуктивности L, конденсатора емкостью C и резистора с сопротивлением R

Передаточные функции всех фильтров, участвующих в спектральном анализе, полагаем известными. Резонансные кривые, показанные на фиг.1, представляют собой зависимости от частоты модулей этих функций.

Если S(ω) - комплексный спектр анализируемого сигнала и сигнал этот проходит через i-й фильтр с передаточной функцией W_i(ω), то комплексный спектр сигнала на выходе фильтра будет определяться произведением W_i(ω)S(ω), а сам сигнал - обратным преобразованием Фурье этого произведения:

Будем полагать, что спектр входного сигнала сосредоточен в диапазоне анализируемых частот с нижней частотой интервала ω_н и верхней частотой ω_в. Тогда (2) перепишется в виде

Разобьем диапазон анализируемых частот на элементы разрешения с шагом дискретизации Ω, размер которого определяется желаемыми точностью и разрешением по частоте и значительно меньше полос пропускания фильтров. Примерное соотношение ширины резонансной кривой фильтра и элемента разрешения показано на фиг.2. Такая дискретизация позволяет записать (3) в виде суммы

где K - число элементов разрешения в диапазоне контролируемых частот, k - номер элемента разрешения, W_i(kΩ) и S(kΩ) - значения соответственно передаточной функции i-го фильтра и комплексного спектра сигнала в k-м элементе разрешения.

Обозначим

и

С учетом этих обозначений перепишем (4) в виде

где

- векторы размером K×1.

Вектор (7) известен: он определяется дискретными значениями передаточной функции i-го фильтра и размером элемента разрешения Ω. Вектор (8) представляет собой дискретизированный вариант комплексного спектра анализируемого сигнала, причем дискретность отсчетов по частоте равна выбранному размеру элемента разрешения Ω.

Зафиксируем в момент времени t значения сигналов на выходах всех фильтров гребенки:

Систему уравнений (9) запишем в векторно-матричном виде:

где - вектор измерений,

комплексная матрица размером K×N. Подставив (7) и (5a) в (11), получим явное выражение для компонент этой матрицы в момент t:

В уравнении (10) вектор g(t) и матрица V(t) известны, a s - искомый вектор, который содержит составляющие комплексного спектра анализируемого сигнала, отстоящие одна от другой по частоте на величину Ω.

Если необходимо учитывать ошибки измерений сигналов на выходах фильтров, то уравнение (10) принимает вид уравнения измерений

где n(t) - вектор ошибок измерений.

Для определения спектральной плотности сигнала с точностью элемента разрешения достаточно решить уравнение (10) или (13) относительно вектора s. Существуют различные методы решения этих уравнений (см., например, [4]). Так, можно использовать метод псевдообращения матрицы, который дает решение уравнения (10) с минимальной среднеквадратической ошибкой:

где обозначает оценку вектора s, а+ - операцию псевдообращения матрицы.

Чтобы найти оценку вектора s из уравнения измерений (13), можно воспользоваться методом винеровского оценивания, согласно которому

,

где R_ss и R_nn - корреляционные матрицы соответственно сигнала и ошибок измерений.

Если отсутствует информация о корреляционной матрице вектора-оригинала R_ss, то компоненты этого вектора будем полагать δ-коррелированными с известной и одинаковой для всех компонент дисперсией Тогда где I - единичная матрица и

Наконец, в случае отсутствия информации и о статистических характеристиках ошибок измерений, можно воспользоваться оценкой по методу псевдообращения (14).

Полученная оценка вектора s является оценкой спектральной плотности анализируемого сигнала с точностью элемента разрешения Ω. Разрешающая способность заявляемого способа определяется тем же элементом разрешения Ω. Действительно, согласно (5б) и (8), компонентами полученного в результате оценивания вектора являются оценки спектральной плотности анализируемого сигнала с дискретностью Ω. И при этом компоненты вектора s являются комплексными и определяют как амплитудные, так и фазовые составляющие спектральной плотности сигнала.

Операция псевдообращения матрицы, используемая в (14), выполнима не только с квадратной, но и с прямоугольной матрицей. Поэтому уравнения (10) и (13) будут иметь решения в наиболее привлекательном случае, когда число элементов разрешения больше числа используемых фильтров (K>N). Это принципиально позволяет при анализе спектра достигать разрешения, в разы превышающего разрешение прототипа, которое ограничивается числом используемых фильтров и шириной их резонанасных характеристик, в то время как в заявляемом способе разрешение определяется выбранным размером элемементов разрешения. То же относится и к точности, которая, согласно [2], находится в прямой связи с разрешением.

Преимущества предлагаемого способа по сравнению с прототипом следующие.

1. Возможность анализа не только амплитудного, но и фазового спектра, т.е. комплексного спектра в целом.

2. Точность и разрешение спектрального анализа определяются выбранным размером элемента разрешения и могут в разы превосходить точность и разрешение прототипа, которые ограничиваются числом используемых фильтров и шириной их резонансных кривых.

3. Точность и разрешение в завляемом способе не связаны с добротностью используемых резонаторов, как это имеет место в прототипе. Поэтому высокие точность и разрешение могут достигаться при относительно низкодобротных фильтрах-резонаторах, которые обладают меньшим временем переходных процессов, чем высокодобротные резонаторы. За счет этого высокие точность и разрешение достигаются без увеличения времени спектрального анализа.

4. Число элементов разрешения (K) не связано с числом фильтров, в результате чего можно достигать высоких точности и разрешения при ограниченном числе фильтров (N), в то время как в прототипе повышение точности и разрешения достигаются увеличением числа высоко добротных фильтров.

Источники информации

1. Самойленко В.И., Пузырев В.А., Грубрин И.В. Техническая кибернетика: Учеб. пособие. - М.: Изд-во МАИ, 1994, стр.223-226.

2. Харкевич А.А. Спектры и анализ. - М., Государственное изд-во технико-теоретической литературы, 1952, стр.93-97 (прототип), стр.109.

3. Справочник по радиоэлектронике в трех томах: Под общей ред. А.А.Куликовского. Том 1. - М. «Энергия», 1967, стр.184.

4. Самойленко М.В. Математические аспекты применения томографического подхода в обработке многоканальных сигналов. // Вестник Московского авиационного института, № 3, 2010.

Способ спектрального анализа электрического сигнала, заключающийся в том, что анализируемый электрический сигнал подают одновременно на гребенку фильтров, представляющих собой резонаторы, настроенные на различные частоты и измеряют сигналы на выходах этих фильтров, отличающийся тем, что до проведения измерений диапазон контролируемых частот разбивают на элементы разрешения с шагом дискретизации Ω, соответствующим желаемым точности и разрешению спектрального анализа и существенно меньшим полос пропускания используемых фильтров, определяют дискретные значения комплексной передаточной функции каждого фильтра во всех элементах разрешения W_i(Ω), W_i(2Ω),… W_i(KΩ), где i - номер фильтра, К - число элементов разрешения в диапазоне контролируемых частот, формируют матрицу где N - число фильтров, a j - комплексная единица, в некоторый момент времени t фиксируют значения сигналов на выходах всех фильтров и объединяют их в вектор g(t)=[g₁(t) g₂(t)… g_N(t)]^T, где g_i(t) - сигнал на выходе i-го фильтра в момент времени t, Т означает транспонирование, определяют искомый комплексный спектр анализируемого сигнала в дискретизированном виде с шагом дискретизации Ω, решая относительно вектора s векторно-матричное уравнение g(t)=V^T(t)s, где s=[S(Ω)S(2Ω)…S(KΩ)]^T, S(kΩ) - значение комплексного спектра анализируемого сигнала, приходящееся на k-й элемент разрешения, при этом решение находят одним из методов линейной алгебры, например, методом псевдообращения , где + обозначает операцию псевдообращения матрицы, - оценка вектора s, или при необходимости учитывать ошибки измерений, оценку вектора s находят методом оценивания из уравнения измерений g(t)=V^T(t)s+n, где n - вектор ошибок измерений сигналов на выходах фильтров.