Способ определения моментов синхронного и асинхронного поведения двух связанных систем

Способ определения моментов синхронного и асинхронного поведения двух связанных систем

Иллюстрации

Показать все

Реферат

Изобретение относится к областям радиофизики и нелинейной динамики и может найти применение при анализе поведения систем различной природы по временным рядам, содержащим некоторые характерные (синхронные и асинхронные) участки поведения. Изобретение может быть эффективно использовано в задачах анализа некоторых типов перемежающегося поведения, имеющих место, в частности, на границе фазовой синхронизации и синхронизации временных масштабов хаотических генераторов.

В настоящее время известны способы определения моментов синхронного и асинхронного поведения (ламинарных и турбулентных участков, соответственно) в перемежающихся временных реализациях систем, основанные на анализе "текущего" периода или амплитуды колебаний системы [Берже П., Помо И., Видаль К. Порядок в хаосе. М.: Мир, 1991, Г.Шустер. Детерминированный хаос. М.: Мир, 1988 и др.]. Существуют также методы выделения ламинарных и турбулентных участков, основанные на использовании непрерывного вейвлетного преобразования [Короновский А.А., Храмов А.Е. Письма в ЖТФ 27(1), (2001), 3-11; Короновский А.А., Москаленко О.И., Попов П.В., Храмов А.Е. Способ выделения характерных фаз поведения систем по временным данным. Патент на изобретение №2337610, 2008]. Эти методы позволяют эффективно определять моменты возникновения синхронизации в частных случаях, например, когда участки асинхронного поведения (турбулентные участки) характеризуются существенно большей амплитудой колебаний по сравнению с синхронными (ламинарными) участками [Г.Шустер. Детерминированный хаос. М.: Мир, 1988], или когда наличие характерных участков поведения отчетливо видно по самой временной реализации системы или временного ряда, полученного путем линейной комбинации соответствующих ей координат [Короновский А.А., Храмов А.Е. Письма в ЖТФ 27(1), (2001), 3-11; Короновский А.А., Москаленко О.И., Попов П.В., Храмов А.Е. Способ выделения характерных фаз поведения систем по временным данным. Патент на изобретение №2337610, 2008].

Однако подобные методы оказываются неприменимыми для анализа перемежающегося поведения, имеющего место на границе возникновения фазовой синхронизации и синхронизации временных масштабов двух связанных хаотических систем, где в роли основной анализируемой переменной используются мгновенные фазы, точнее разность мгновенных фаз рассматриваемых систем.

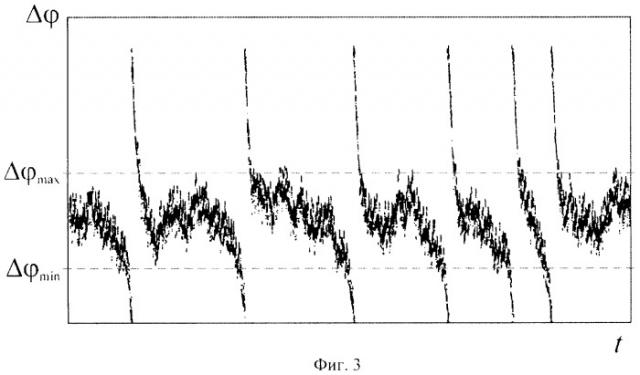
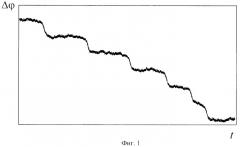
Для определения моментов синхронного и асинхронного поведения в таких случаях традиционно вводят в рассмотрение мгновенные фазы хаотических сигналов, соответствующих взаимодействующим системам, одним из нижеперечисленных способов: как угол поворота на плоскости проекции хаотического аттрактора, с помощью сечения Пуанкаре или преобразования Гильберта, с помощью непрерывного вейвлетного преобразования [Pikovsky A., Rosenblum М., Kurths J. // Int. J. Bifurcation and Chaos. 2000. V.10. N.10. P.2291-2305; Pikovsky A., Rosenblum M., Osipov G., Kurths J. // Physica D. 1997. V.104. N4. P.219-238; Hramov A.E., Koronovskii A.A. An approach to chaotic synchronization. CHAOS. 14, 3 (2004) 603-610]. При этом фазу хаотического сигнала считают монотонно возрастающей. Тогда разность фаз в режиме перемежаемости будет представлять собой последовательность участков с синхронным (где разность фаз изменяется в пределах 2π - ламинарные участки) и асинхронным (разность фаз демонстрирует монотонный рост или спад - турбулентные участки) поведением (см. фиг.1). Участки синхронного и асинхронного поведения на зависимости разности фаз от времени легко определяются визуально [Park E.-H. Et al. Phys. Rev. E 60 (1999) 6627; Zaks M.A. et al. Phys. Rev. Lett. 82 (1999) 4228].

Однако при численном выделении этих участков возникает ряд проблем, связанных с хаотическими флуктуациями, которые приводят к ложному детектированию моментов возникновения синхронного и асинхронного поведения. Таким образом, указанный метод не обеспечивает точное определение моментов синхронного и асинхронного поведения связанных систем и приводит к некорректным результатам при анализе длительных временных данных.

Задачей настоящего изобретения является разработка способа определения моментов синхронного и асинхронного поведения двух связанных систем, находящихся вблизи границы фазовой синхронизации и синхронизации временных масштабов.

Техническим результатом изобретения является возможность точного определения моментов синхронного и асинхронного поведения двух связанных систем, находящихся вблизи границ фазовой синхронизации и синхронизации временных масштабов.

Поставленная задача решается тем, что согласно способу определения моментов синхронного и асинхронного поведения двух связанных систем производят запись сигналов, производимых связанными системами, рассчитывают мгновенные фазы колебаний взаимодействующих систем, вычисляют разность между значениями фаз связанных систем для каждого момента времени, приводят мгновенные значения фаз колебаний и разностей между значениями фаз в ограниченный диапазон [0; 2π], задают пороговые значения разности между значениями фаз Δφ_min и Δφ_max, такие, что π/2<Δφ_max - Δφ_min<π, π/2<(Δφ_max+Δφ_min)/2<π, при этом определяют поведение двух связанных систем как синхронное в моменты времени, когда Δφ_min <Δφ<Δφ_max, а моменты асинхронного поведения двух связанных систем соответствуют времени, при котором Δφ<Δφ_min или Δφ>Δφ_max.

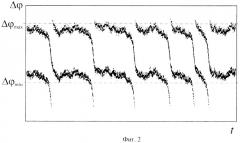
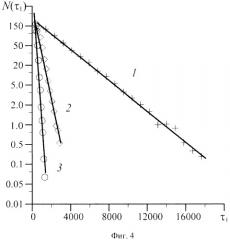
Изобретение поясняется чертежами, где на фиг.1-3 представлены качественные картины изменения разности фаз Δφ(t) с течением времени (на примере двух однонаправлено связанных систем Ресслера со слегка различающимися параметрами) для случаев: фиг.1 - когда мгновенные фазы монотонно возрастают от -∞ до +∞; фиг.2 - когда мгновенные фазы лежат в диапазоне [-2π; 2π]; фиг.3 - когда диапазон изменения разности мгновенных фаз составляет 2π. На фиг.4 показаны распределения длительностей участков синхронного поведения N(τ₁) в системе двух однонаправлено связанных генераторов Ресслера при различных значениях параметра связи и соответствующие аппроксимации (показаны сплошными линиями): 1 - ε=0.036 (+), N(τ₁)=213exp(-4×10^-4τ₁); 2 - ε=0.032 (◇), N(τ₁)=369ехр(-2×10^-3τ₁); 3 - ε=0.028 (Ο), N(τ₁)=1211exp(-7×10^-3τ₁).

Заявляемый способ определения моментов синхронного и асинхронного поведения двух связанных систем, находящихся вблизи границы фазовой синхронизации или синхронизации временных масштабов, заключается в следующем. Производят запись сигналов, генерируемых связанными системами, находящимися вблизи границы фазовой синхронизации или синхронизации временных масштабов (например, регистрируют колебания электрического напряжения в различных участках цепи). Для полученных сигналов рассчитывают мгновенные фазы φ₁(t) и φ₂(t) колебаний таким образом, чтобы они лежали в пределах [0; 2π]. В этом случае разность между фазами Δφ(t)=φ₂(t)-φ₁(t) изменяется в диапазоне [-2π; 2π] (фиг.2) и является многозначной. Для устранения многозначности величину разности фаз Δφ переводят из диапазона значений шириной 4π к аналогичному диапазону шириной 2π, используя свойство 2π-периодичности фазы. После этого для наглядности строят график зависимости разности фаз от времени Δφ(t), на котором различают участки, демонстрирующие один из двух характерных типов поведения - синхронный (ламинарный) или асинхронный (турбулентный). Участки асинхронной динамики (турбулентного поведения) характеризуются изменением Δφ для каждого последующего промежутка времени на величину δ>π/2, а участки синхронной динамики выглядят на графике как колебание значений Δφ около стационарной величины с амплитудой, значение которой не превышает δ<π/2. Как показано на фиг.3, значения разности фаз, соответствующие синхронному поведению системы, расположены в средней части диапазона значений. Это позволит диагностировать начало и конец участка асинхронной динамики по пересечению величиной Δφ(t) некоторых заранее установленных пороговых значений Δφ_min и Δφ_max, таких, что π/2<Δφ_max-Δφ_min<π, π/2<(Δφ_max+Δφ_min)/2π.

Следует отметить, что в данном случае все флуктуации величины Δφ(t), обычно препятствующие точному детектированию моментов синхронного или асинхронного поведения, оказываются сосредоточенными в области значений [Δφ_min; Δφ_max], соответствующей синхронному поведению систем, что позволяет избавиться от сложностей нахождения границ участков синхронной и асинхронной динамики и привести к точному определению момента характерного участка поведения.

В качестве примера конкретной реализации заявляемого способа определения моментов синхронного и асинхронного поведения рассмотрим поведение двух однонаправлено связанных систем Ресслера, являющихся моделями радиотехнических генераторов низкочастотного диапозона [Rico-Martinez R., Kreischer K.E., Flatgen G., Anderson J.S., Kevrekidis I.G. Adaptive Detection of Instabilities: An Experimental Feasibility Study // Physica D. 176, 2003, 1], вблизи границы фазовой синхронизации:

где x_d,r(t)=(x_d,r, y_d,r, z_d,r) - векторы состояния ведущей и ведомой систем (представляющие собой записи колебаний напряжений x_d,r, y_d,r, z_d,r, снимаемых в различных участках цепи), соответственно (индекс d отвечает ведущей системе, индекс r - ведомой), а=0.15, р=0.2, с=10, ω_d=0.99, ω_r=0.95 - управляющие параметры, определяемые параметрами схемы, ε - параметр связи. Известно, что при выбранных значениях управляющих параметров ниже порога возникновения фазовой синхронизации ε_c=0.042 в системе (1) наблюдается перемежающееся поведение типа «игольное ушко» [Куровская М.К. Распределение длительностей ламинарных фаз при перемежаемости «игольного ушка». Письма в ЖТФ. 34, 24 (2008) 48-54]. Одной из характеристик этого типа перемежаемости является экспоненциальный закон распределения длительностей участков синхронного поведения. Для верификации заявляемого способа покажем, что аналогичные зависимости имеют место в системе (1) при различных значениях параметра связи ε<ε_c. Указанные зависимости приведены на фиг.4. Отчетливо видно, что распределение длительностей синхронных участков, выделенных заявляемым способом, подчиняется экспоненциальному закону, в полном соответствии с известной закономерностью.

Таким образом, положительным эффектом заявляемого способа определения моментов синхронного и асинхронного поведения двух связанных систем является его простота: он не требует дополнительных преобразований фаз анализируемых сигналов, что позволяет существенно упростить и ускорить процедуру выделения участков синхронного и асинхронного поведения двух связанных систем.

Способ определения моментов синхронного и асинхронного поведения двух связанных систем, заключающийся в том, что производят запись сигналов, производимых связанными системами, рассчитывают мгновенные фазы колебаний взаимодействующих систем, вычисляют разность между значениями фаз связанных систем для каждого момента времени, приводят мгновенные значения фаз колебаний и разностей между значениями фаз в ограниченный диапазон [0; 2 π], задают пороговые значения разности между значениями фаз Δφ_min и Δφ_max, такие, что π/2<Δφ_max-Δφ_min<π, π/2<(Δφ_max+Δφ_min)/2<π, при этом определяют поведение двух связанных систем как синхронное в моменты времени, когда Δφ_min<Δφ<Δφ_max, а моменты асинхронного поведения двух связанных систем соответствуют времени, при котором Δφ<Δφ_min или Δφ>Δφ_max.