Способ подавления ошибок многолучевости в приемнике спутниковой навигации

Способ подавления ошибок многолучевости в приемнике спутниковой навигации

Иллюстрации

Показать все

Реферат

Изобретение относится к области спутниковой радионавигации, конкретно к способам получения измерений псевдодальности и псевдоскорости в условиях многолучевости в навигационных приемниках Спутниковых Радионавигационных Систем (СРНС).

В мире существуют или создаются несколько СРНС. Это действующие системы Global Positioning System GPS (США), Глобальная Навигационная Спутниковая Система ГЛОНАСС (Российская Федерация) и создаваемые Galileo (Европейское Космическое Агенство ESA), BeiDou или Compass (КНР). Настоящее изобретение может быть использовано в навигационных приемниках всех этих или других СРНС.

Применение навигационных приемников в условиях городского каньона подводит к частому пропаданию прямой видимости спутников. Принимаемая мощность сигналов при этом становится низкой или пропадает. В этих условиях традиционное автономное сопровождение сигналов в системе с замкнутым контуром с помощью систем слежения за задержкой (ССЗ) и частотной автоподстройки (ЧАП) часто прерывается.

Слежение за сигналами от спутников в системе с разомкнутым контуром («Open-Loop Tracking» [патент США 6633255, опубл. 04.07.2002]) реализуется посредством вычисления для каждого спутника прогнозов измерений задержки и частоты на основе навигационного решения, формирования двумерной (по задержке и частоте) решетки мощностей с центром, определяемым прогнозом измерений, получения поправок к прогнозу и формирования измерений как суммы поправок с прогнозом. Такое слежение сохраняет работоспособность при низких отношениях сигнал/шум.

Пропадание сигнала части спутников в системе, реализующей слежение в разомкнутом контуре, не является критичным до тех пор, пока существует навигационное решение, то есть остаются измерения по 3-4 сигналам спутников.

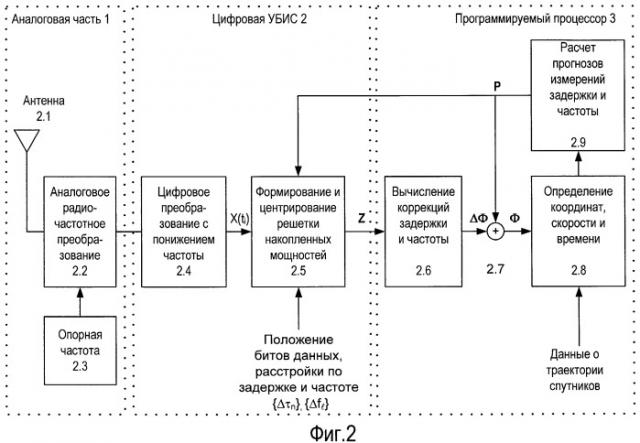
Наличие сигналов, приходящих по прямому и отраженным лучам, приводит к появлению ошибок как задержки, так и частоты. На Фиг.1 приводится пример схемы распространения многолучевого сигнала, приводящей к искажениям измерений:

- для статического приемника или приемника, движущегося параллельно отражающей поверхности (Фиг.1, а)), возникают только ошибки измерения задержки, так как скорости изменения дальности до спутника для прямого и отраженного лучей равны,

- для приемника, движущегося в направлении отражающей поверхности (Фиг.1, б)), к ошибкам измерения задержки добавляются ошибки измерения частоты, так как в этом случае скорость изменения дальности до спутника по отраженному лучу отличается от скорости изменения дальности до спутника по прямому лучу.

Известны способы, которые обеспечивают уменьшение ошибок измерения псевдодальности, возникающих в результате наличия отраженных лучей. Это в основном узкоапертурный коррелятор [Theory and Performance of Narrow Correlator Spacing in a GPS receiver. A.J. van Dierendonck, Pat Fenton, Tom Ford. Journal of The Institute of Navigation, Vol.39, No.3, 1992], стробовые методы формирования реплики псевдослучайной последовательности (ПСП) сигнала при вычислении автокорреляционной функции (АКФ) [патент США №7436356, опубл. 03/24/2006], методы, основанные на использовании переднего фронта АКФ, вычислении пересечения отрезков на переднем и заднем фронтах и взвешивании отсчетов автокорреляционной функции [патент США №7436356, опубл. 03/24/2006]. Эти методы легко реализуются в недорогих массовых приемниках и уменьшают ошибку псевдодальности, но точность их невысока.

Также известны методы подавления многолучевости, основанные на оптимальной обработке многолучевого сигнала, включающие в себя измерение параметров сигналов, приходящих по прямому и отраженному лучам, с применением метода максимального правдоподобия. Подавление влияния сигналов, приходящих по отраженным лучам производится путем их оптимальной оценки и исключения из наблюдений. Эти методы используются в дорогостоящих геодезических приемниках и требуют значительных аппаратных затрат для реализации.

Применение адаптивных антенных решеток для подавления сигналов, приходящих по отраженным лучам, требует нескольких приемных антенн и дополнительной обработки принимаемых ими сигналов, что также значительно усложняет аппаратуру потребителя.

Наиболее близким к заявляемому решению является способ, описанный в патенте США 6031881, опубл. 02.02.2000. Такой метод уменьшения влияния многолучевости на измерения задержки сигнала от спутника заключается в том, что:

1) принимают сигнал, имеющий информацию о дальности и включающий в себя в том числе искажающий сигнал, приходящий по второму (отраженному) лучу, и переносят принятый сигнал на нулевую частоту;

2) квантуют преобразованный сигнал синхронно с моделирующей формой волны, создавая квантованный сигнал и комбинируя успешные повторения множества фронтов содержащих информацию о дальности;

3) коррелируют комбинированный сигнал с множеством искусственно задержанных представлений переданного квантованного сигнала приемника;

4) вычисляют оценку максимального правдоподобия дальности с использованием выбранных пар представлений принятого сигнала;

5) ограничивают относительную амплитуду сигнала, приходящего по второму лучу, основываясь на представлениях об условиях передачи сигнала;

6) вычисляют вторую оценку максимального правдоподобия псевдодальности наряду с ограничением относительной амплитуды сигнала, приходящего по второму лучу, используя представление передаваемого сигнала.

Недостатками этого метода являются необходимость сохранения входных выборок сигнала, квантованных на высокой частоте (в патенте указывается частота дискретизации, равная 20 МГц для системы GPS), и обработки этих выборок в реальном масштабе времени. Для реализации такого метода требуется большой объем памяти и высокая скорость обработки информации.

Другим недостатком является ограниченное время накопления. Причиной ограничения времени накопления является модуляция принимаемого сигнала неизвестными битами данных навигационного сообщения передаваемого сигнала (каждые 20 мс для GPS и ГЛОНАСС), что приводит к ограничению принимаемого отношения мощности несущей сигнала С к мощности шума N₀ в полосе 1 Гц С/N₀ > 30 дБ Гц.

Задачей предлагаемого изобретения является устранение влияния многолучевости на измерения задержек и частоты и создание способа, работоспособного для слабых сигналов и не требующего больших вычислительных затрат для реализации.

Достигаемый технический результат - обеспечение бит-синхронного формирования решетки накопленных мощностей и подавление ошибок многолучевости путем построения функции правдоподобия с исключением мешающих параметров.

Поставленная задача решается следующим образом.

Способ подавления ошибок многолучевости в приемнике спутниковой навигации включает операции поиска сигналов навигационных спутников, прием и обработку комплексных сигналов каждого спутника, сопровождение найденных сигналов следящим разомкнутым контуром и определение координат, скорости приемника и точного времени по измерениям задержки и частоты сигнала прямого и отраженных лучей согласно следующему:

на основании навигационных параметров, включающих в себя координаты, скорость приемника и точное время, а также информации о движении спутника, полученной на основании измеренного времени и принятых эфемерид, рассчитываются прогнозы задержки и частоты, предназначенные для ориентации двумерной решетки накопленных мощностей по задержке и частоте, которая формируется на основании принятых и обработанных комплексных сигналов. При этом в процессе формирования элементов решетки осуществляют суммирование комплексного сигнала на интервале когерентного накопления синхронно с битами данных данного спутника, причем время когерентного накопления согласовано с длиной бита. На основании обработки решетки накопленных мощностей, включающей ее центрирование, вычисляют коррекции к прогнозам задержки и частоты, а измерения задержки и частоты вычисляют как суммы прогнозов с соответствующими коррекциями. После этого производят экстраполяцию полученных измерений на заданный момент времени и расчет измерений псевдодальности и псевдоскорости, а на основании измерений, полученных от всех спутников, определяют координаты и скорость приемника. Вычисление коррекций задержки и частоты содержит этапы, на которых:

вычисляют коррекции однолучевого сигнала с использованием центрированной решетки накопленных мощностей,

выявляют, имеет ли место многолучевость, и

при положительном результате этого выявления осуществляют уточнение коррекций с привлечением весовых коэффициентов,

при этом уточнение коррекций осуществляют путем формирования функции правдоподобия на основании вектора центрированных накопленных мощностей и осуществляют коррекцию согласно найденному глобальному максимуму функции правдоподобия.

Формирование функции правдоподобия на основании вектора центрированных накопленных мощностей возможно различными способами, например двумя описанными ниже.

В первом способе формирование функции правдоподобия на основании вектора центрированных накопленных мощностей включает следующие подэтапы:

- вычисление взвешенных сумм для каждого вектора с привлечением векторов весовых коэффициентов, соответствующих предполагаемым задержкам сигналов прямого и отраженных лучей,

- получение матриц, обратных матрицам, построенным на основании попарных скалярных произведений векторов весовых коэффициентов, и

- вычисление функции правдоподобия как квадратичной формы с результатами первого и второго подэтапов.

Во втором способе формирование функции правдоподобия на основании вектора центрированных накопленных мощностей включает следующие подэтапы:

- вычисление взвешенных сумм для каждого вектора с привлечением ортонормированных векторов сигналов, зависящих от задержек сигналов прямого и отраженного лучей,

- вычисление функции правдоподобия путем вычисления суммы квадратов полученных взвешенных сумм.

Формирование функции правдоподобия для уменьшения ошибок измерения частоты производится аналогично.

В первом случае включает следующие подэтапы:

- вычисление взвешенных сумм для каждого вектора с привлечением векторов весовых коэффициентов, соответствующих предполагаемым частотам сигнала прямого и отраженного лучей,

- получение матриц, обратных матрицам, построенным на основании попарных скалярных произведений векторов весовых коэффициентов, и

- вычисление функции правдоподобия как квадратичной формы с результатами первого и второго подэтапов.

Во втором случае:

- вычисление взвешенных сумм для каждого вектора с привлечением ортонормированных векторов сигналов, зависящих от частот сигналов прямого и отраженного лучей,

- вычисление функции правдоподобия путем вычисления суммы квадратов полученных взвешенных сумм.

Изобретение иллюстрируется чертежами, на которых:

Фиг.1 представляет схему распространения многолучевого сигнала, приводящую к искажениям:

а) только по задержке,

б) по доплеровскому смещению и задержке.

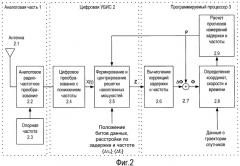
Фиг.2 - схема навигационного приемника со слежением в системе с разомкнутым контуром.

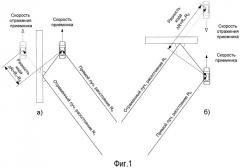
Фиг.3 - блок-схема формирования одного элемента решетки накопленных мощностей.

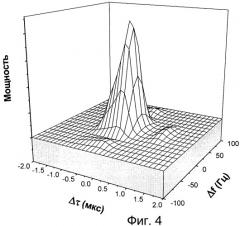
Фиг.4 - пример двумерной решетки накопленных мощностей, сформированной в результате приема многолучевого сигнала.

Фиг.5 - решетка накопленных мощностей, соответствующая доплеровской частоте максимальной мощности сигнала, до и после центрирования.

Фиг.6 - блок-схема центрирования решетки накопленных мощностей.

Фиг.7 - блок-схема вычисления измерений с устранением воздействия многолучевости.

Фиг.8 - блок-схема варианта реализации вычисления коррекций заявленным способом устранения воздействия многолучевости с использованием векторов сигнала S^ij=Q^-1/2P^ij и обратных матриц (S^ijTS^ij)^-1

Фиг.9 - блок-схема варианта реализации вычисления коррекций заявленным способом устранения воздействия многолучевости с использованием ортонормированных векторов сигналов V^ij.

Фиг.10 - пример функции правдоподобия y(τ₀, τ₁) для многолучевого сигнала.

Фиг.11 - проекция функции правдоподобия y(τ₀, τ₁) и оценки задержек прямого и отраженного лучей.

Фиг.12 - ошибки оценки задержки сигнала, приходящего по прямому лучу, рассчитанные согласно заявляемому способу.

Фиг.13 - ошибки оценки задержки сигнала, приходящего по прямому лучу, рассчитанные для узкоапертурного коррелятора.

Фиг.14 - ошибки оценки задержки сигнала, приходящего по прямому лучу, рассчитанные для стробового коррелятора.

Фиг.15 - сравнение ошибок оценки псевдодальности заявляемого способа и узкоапертурного коррелятора.

Фиг.16 - ошибки измерения координат при использовании узкоапертурного коррелятора.

Фиг.17 - ошибки измерения координат при использовании заявленного способа.

Ниже раскрывается пример осуществления изобретения.

Схема типового СРНС приемника со слежением в системе с разомкнутым контуром приводится на Фиг.2.

Обработка сигналов в типовом навигационном приемнике разделяется на аналоговую (блок 1) и цифровую (блоки 2, 3). Часть цифровой обработки сигналов, требующая высокой скорости вычислений и не требующая сложных алгоритмов обработки, выполняется на цифровой ультрабольшой интегральной схеме (УБИС) 2. Другая часть, требующая сложных алгоритмов обработки в невысоком темпе, выполняется, как правило, на программируемом процессоре 3.

Принимаемые антенной (2.1) радиочастотные электромагнитные сигналы преобразуются в электрические и усиливаются. Далее на этапе 2.2 производится аналоговое радиочастотное преобразование, а именно производится перенос с радиочастоты на промежуточную частоту, а также производится дискретизация аналогового сигнала по времени и квантование его по уровню. Для переноса и дискретизации используется опорная частота, получаемая на этапе 2.3 с помощью генератора опорной частоты. Далее цифровой сигнал подвергается цифровому преобразованию с понижением частоты на этапе 2.4. Для этого цифровой сигнал переносится на близкую к нулевой частоту, ограничивается по спектру в заданной полосе частот и децимируется в соответствии с частотой Найквиста. Этот сигнал X(t_i) является цифровым комплексным сигналом с ограниченной в целях экономии памяти разрядностью. Он содержит аддитивную смесь принимаемых от спутников сигналов и шума. Далее полученный комплексный сигнал X(t_i) используется на этапе 2.5 для формирования и центрирования решетки накопленных мощностей Z. Также для формирования решетки накопленных мощностей используются прогнозы задержки и частоты P=(τ_p,f_p)^T, где Р - вектор прогнозов, τ_р - прогноз задержки, f_p - прогноз частоты, и значения расстройки элементов решетки накопленных мощностей относительно прогноза по задержке {Δτ_n} и частоте {Δf_ℓ}.

Далее на этапе 2.6 на основании центрированной решетки накопленных мощностей Z производится вычисление коррекций ΔФ (относительно прогнозов) задержки и частоты

,

где Δτ_р - коррекция задержки,

Δf_p - коррекция частоты.

На этапе 2.7 полученные коррекции складываются с прогнозами задержки и частоты для получения измерений задержки и частоты

,

где Ф=(τ,f)^T - вектор измерений задержки τ и частоты f.

Полученные измерения Ф задержки и частоты служат вместе с данными о траектории и скорости спутника (эфемеридами) для определения на этапе 2.8 координат, скорости и времени приемника (при этом вычисление псевдодальности и псевдоскорости на основании измерений задержки и частоты производится стандартным способом). На этапе 2.9 на основании полученных координат, скорости и времени, а также данных о траектории и скорости спутника производится расчет прогнозов Р измерений задержки и частоты.

Этапы 2.3 и 2.4 осуществляются в аналоговой части 1, этапы 2.4 и 2.5 - в цифровой ультрабольшой интегральной схеме 2 (УБИС), этапы 2.6-2.9 - в программируемом процессоре 3.

Система со слежением в разомкнутом контуре сохраняет работоспособность для слабых сигналов с отношением мощности несущей к мощности шума в полосе 1 Гц c/N₀ > 10 дБ Гц, где С - мощность несущей, N₀ - мощность шума в полосе 1 Гц.

Блок-схема формирования одного элемента решетки накопленных мощностей с индексом n, k (n - номер задержки, k - номер частоты) изображена на Фиг.3.

Смеситель кода (этап 3.1) осуществляет умножение выборок комплексного сигнала на значения вещественной реплики кода:

где - комплексный сигнал с выхода n-го смесителя кода,

X(t_i) - выборка комплексного сигнала с выхода этапа 2.4,

i - номер выборки комплексного сигнала,

t_i=δ*i - время i-й выборки сигнала,

δ - интервал дискретизации,

C_p(t) - значение реплики кода сигнала в момент времени t,

- задержка реплики сигнала для n-го смесителя кода,

τ_р - прогноз задержки,

Δτ_n - значение расстройки по задержке для n-го смесителя кода,

f_p - прогноз частоты Доплера,

F - радиочастота несущей.

Смеситель несущей (этап 3.2) осуществляет умножение комплексного сигнала на выходе смесителя кода 3.1 на комплексную экспоненту:

где - комплексный сигнал на выходе ℓ-го смесителя несущей и n-го смесителя кода,

j - мнимая единица,

- значение частоты Доплера для ℓ-го смесителя несущей,

f_p - прогноз частоты Доплера,

Δf_ℓ - значение расстройки по частоте для ℓ-го смесителя несущей.

Когерентный накопитель 3.3 осуществляет суммирование комплексного сигнала на интервале когерентного накопления T_coh=N_coh*δ синхронно с битами данных данного спутника, причем время когерентного накопления согласовано с длиной бита (20 ms для систем GPS и ГЛОНАСС):

где - комплексный сигнал на выходе когерентного накопителя на р-м интервале когерентного накопления,

t_m=δ*N_coh*p - время р-го интервала когерентного накопления,

Ncoh - количество выборок комплексного сигнала на интервале когерентного накопления.

Блок вычисления мощности 3.4 вычисляет квадрат модуля комплексного сигнала с выхода когерентного накопителя:

где - вещественная мощность сигнала на на р-м интервале когерентного накопления,

Re(), Im() - вещественная и мнимая части комплексного сигнала.

Так как комплексный сигнал на выходе когерентного накопителя синхронизирован с битами данных, мощность этого сигнала не зависит от изменения знака данных в сигнале.

Некогерентный накопитель 3.5 суммирует мощности на интервале некогерентного накопления T_inc=T_coh*N_inc:

где Z_nℓ - мощность сигнала на выходе некогерентного накопителя на одном интервале некогерентного накопления,

N_inc - количество выборок вещественных мощностей сигнала на интервале некогерентного накопления.

Аналогичные операции выполняются для вычисления каждого элемента накопленных мощностей с другими значениями расстроек по задержке Δτ_n и частоте Δf_ℓ относительно прогнозов. Пример решетки накопленных мощностей, сформированной в результате приема многолучевого сигнала с отличием сигнала, приходящего по отраженному лучу, только по задержке (см. Фиг.1, а)), приводится на Фиг.4.

Вычисленные накопленные мощности представляют из себя сумму мощностей сигнала и шума. Неизвестная мощность шума представляет из себя мешающий параметр. Для устранения накопленной мощности шума часть элементов решетки накопленных мощностей, не содержащих сигнала, используется для компенсации этой шумовой мощности или центрирования.

На фиг.5 приводится решетка накопленных мощностей, соответствующая одной доплеровской частоте максимального сигнала, до и после центрирования. Здесь для центрирования используются элементы решетки накопленных мощностей в области задержек, меньших, чем задержка прямого луча сигнала.

Блок-схема центрирования приводится на Фиг.6. Центрирование представляет из себя осреднение части элементов решетки накопленных мощностей, не содержащих сигнала, на этапе 6.1 и вычитание полученного среднего значения мощности шума из остальных (или всех) элементов на этапе 6.2.

Вначале рассмотрим статистическую модель наблюдений вектора накопленных мощностей, отличающуюся задержками реплики сигнала и соответствующую одной частоте максимального сигнала.

Модель центрированного вектора Z решетки накопленных мощностей, соответствующая частоте максимального сигнала, может быть записана в виде:

где Z=(z_ℓ1,Z_ℓ2,…,z_ℓN)^T - вектор накопленных мощностей после центрирования, соответствующий всем задержкам и одной частоте максимального сигнала,

N - количество мощностей, соответствующих одной частоте,

τ=(τ₀,τ₁,…,τ_K)^T - вектор задержек сигналов, приходящих по прямому и отраженным лучам, индекс k=0 относится к сигналу прямого луча,

K+1 - общее число лучей,

a=(a₀,a₁,…,a_K)^T - вектор амплитуд сигналов, приходящих по прямому и отраженным лучам,

Δφ=(Δφ₁,Δφ₂,…,Δφ_K)^T - вектор разности фаз сигналов, приходящих по прямому и отраженным лучам (Δφ_κ=φ_κ-φ₀),

Р(τ)=(R₀₀,R₀₁,…,R_0K, R₁₁,R₁₂,…,R_1K,…,R_KK) - матрица размерности (N×(K+1)*(K+2)/2), зависящая от задержки τ₀ сигнала, приходящего по прямому лучу и задержек τ₁, τ₂, …, τ_K сигналов, приходящих по отраженным лучам.

R_km - вектор произведений АКФ сигналов, приходящих по k-му и m-му лучам на элементах решетки накопленных мощностей, определяемый как

τ_k, τ_m - задержки распространения k-го и m-го лучей.

r(τ) - АКФ,

- задержка сигнала на n-м смесителе кода и n-m элементе решетки накопленных мощностей (n=1,…N),

θ(а,Δφ) - вектор, зависящий от амплитуд а и разности фаз Δφ сигналов, приходящих по прямому и отраженным лучам, определяемый как:

ξ=(ξ₁,…,ξ_N)^T - случайный вектор флюктуации шума центрированной решетки накопленных мощностей с математическим ожиданием, равным нулю, и матрицей ковариации Q=<ξξ^T>.

Так как время некогерентного накопления обычно больше или равно 1 секунде, количество некогерентных накоплений решетки мощностей N_inc равно 50 и более. В этих условиях распределение шума стремится к нормальному с нулевым матожиданием и полностью определяется известной ковариационной матрицей Q.

В условиях реального городского каньона количество отраженных лучей может быть большим. Однако наибольшее влияние на ошибки измерения оказывает, как правило, один наиболее сильный отраженный луч. Таким образом, в случае двух лучей (прямого и одного отраженного, K=1) число неизвестных параметров равно 5.

Это:

- квадраты амплитуд сигналов, приходящих по прямому и отраженному лучам, и ,

- косинус разности фаз сигналов, приходящих по прямому и отраженному лучам, cos(Δφ₁),

- задержки сигналов, приходящих по прямому и отраженному лучам, τ=(τ₀,τ₁)^T.

Система уравнений правдоподобия содержит 5 неизвестных, нелинейным образом входящих в нее параметров. Решение такой системы представляет собой сложную вычислительную проблему.

Матрица Р в случае двух лучей (прямого и отраженного) имеет размерность N×3, вектор θ имеет размерность 3×1, где N - количество элементов решетки накопленных мощностей для одной частоты.

Матрица Р и вектор θ для двух лучей сигнала могут быть записаны в виде:

где P₀(τ₀), P₁(τ₁), Р₂(τ₀,τ₁) - векторы размерности (N×1), зависящие от задержек прямого и отраженного лучей, с элементами:

,

,

,

n=1,…,N,

r(τ) - АКФ,

a₀, a₁ - амплитуды сигналов, приходящих по прямому и отраженному лучам,

Δφ=(φ₁-φ₀) - разность фаз сигналов, приходящих по прямому и отраженному лучам.

Если амплитуды и разности фаз сигналов за время накопления решетки накопленных мощностей изменяются, вектор линейных параметров (8) необходимо заменить на осредненный на том же интервале накопления вектор θ. Изменениями матрицы Р на интервале накопления решетки накопленных мощностей можно пренебречь.

На этапах радиочастотного и цифрового преобразований 2.2, 2.4 псевдослучайные навигационные сигналы претерпевают изменения. Эти изменения носят детерминированный характер и полностью определяются известными передаточными функциями используемых фильтров. Эти сигналы вычисляются и используются для предвычисления автокорреляционных функций (АКФ) r(τ) путем умножения на реплику сигнала и накопления. АКФ r(τ) зависят от типа реплики сигнала, ширины полосы приемника и амплитудно-фазовых характеристик используемых в приемнике аналоговых и цифровых фильтров.

Для упрощения расчетов АКФ предвычисляется и табулируется. В дальнейшем АКФ r(τ) считается известной функцией, зависящей от разности задержек принимаемого сигнала и реплики. Вид функции r(τ) также зависит от номера псевдослучайной последовательности (ПСП) GPS и номера частотного канала ГЛОНАСС.

Так как время некогерентного накопления достаточно велико по сравнению с временем когерентного накопления (например, 1 сек и 20 мсек), распределение шума нормализуется. Поэтому в дальнейшем при синтезе метода используется гауссовская модель шума.

Для гауссовского распределения шума в статистической модели наблюдений, описываемой уравнением (6), асимптотически оптимальным методом совместного измерения параметров сигналов, приходящих по прямому и отраженному лучам, является метод максимального правдоподобия (ММП). Функция правдоподобия (ФП) для модели (6) применительно к вектору центрированных накопленных мощностей Z может быть записана в виде:

где

- функция плотности распределения вероятностей центрированного вектора накопленных мощностей Z, которая определяется как:

Эта ФП является нелинейной функцией, зависящей от пяти нелинейных параметров. Нужно найти максимум ФП по всем параметрам уравнения (9). Решение системы пяти нелинейных уравнений правдоподобия представляет собой сложную вычислительную проблему.

Для нахождения максимума ФП (9) по параметрам задержек τ₀, τ₁, используем сначала оценки максимального правдоподобия θ_МП относительно линейной части параметров 6, которые можно получить в явном виде:

После этого полученные оценки θ_МП подставляем в (9) для нахождения максимума ФП y(τ₀,τ₁) по параметрам τ₀, τ₁:

Введем дополнительные обозначения:

S=Q^-1/2P - вектор сигнала после выбеливания шума, зависящий от задержек сигналов прямого и обратного лучей,

X=Q^-1/2Z - центрированный вектор накопленных мощностей после выбеливания шума.

После подстановки S и Х в выражение (11) получим ФП как функцию задержек τ₀, τ₁ в новом виде:

Первое слагаемое уравнения (12) не зависит от параметров τ₀, τ₁, так что необходимо вычислять максимум только второго слагаемого. Способ измерения поправок параметров задержки Δτ₀, Δτ₁ определяется, таким образом, вычислением второго слагаемого в уравнении (12).

Блок-схема вычисления измерений с устранением воздействия многолучевости для слежения в разомкнутом контуре приводится на Фиг.7. На этапе 7.1 двумерная центрированная решетка накопленных мощностей Z используется для вычисления коррекций задержки и частоты ΔФ=(Δτ,Δf)^T однолучевого сигнала с использованием двумерной интерполяции, метода наименьших квадратов или другого известного метода. Затем на этапе 7.2 производится обнаружение многолучевости по отличию формы решетки от эталонной формы для однолучевого сигнала. Если отличия не превышают порога обнаружения многолучевости, то на этапе 7.6 производится вычисление оценок задержки и частоты с полученными коррекциями Ф=(τ,f)^T=Р+ΔФ.

Если многолучевость обнаружена, производится уточнение коррекций ΔФ на этапе 7.3 (подробно описано ниже) и вычисление измерений задержки и частоты на этапе 7.6 с помощью этих коррекций. Набор возможных положений отклонений задержек Δτ_i=τ-τ₀ сигналов, приходящих по прямому лучу, определяется из анализа ошибок используемого метода определения коррекций однолучевого сигнала при наличии отраженного луча. Задержка Δτ_i сигнала, приходящего по отраженному лучу, выбирается в том диапазоне, когда сигнал отраженного луча оказывает влияние на точность измерения задержки прямого луча.

При уточнении коррекций на этапе 7.1 используют весовые коэффициенты, которые могут быть получены, например, из банка весовых коэффициентов на этапе 7.5. Для этого диапазон задержек сигналов прямого и отраженного лучей разбивается на интервалы, для каждого из которых на этапе 7.4 производится предвычисление (возможно вне системы реального времени) весовых коэффициентов, необходимых для вычисления функции правдоподобия, и запись этих предвычисленных коэффициентов в банк весовых коэффициентов.

Блок-схема измерителя в соответствии с уравнением (12) приводится на Фиг.8. На этапе 8.1 производится выбеливание шума (умножение вектора центрированных накопленных мощностей Z на матрицу Q^-1/2):

Матрицу Q^-1/2 можно вычислить, например, разложением на две треугольные по схеме Холецкого и последующим обращением треугольной матрицы [Trefethen L.N., Bau D. Numerical Linear Algebra, SIAM, 1997, стр.172]. Следует отметить, что операция выбеливания шума только уменьшает шум измерений и не влияет на ошибки смещения, вызванные многолучевостью. Моделирование показало, что при отсутствии выбеливания (что соответствует Q=E, где Е - единичная матрица) измерения задержки прямого сигнала при наличии многолучевости остаются несмещенными (Фиг.12). Поэтому операция выбеливания шума является для предложенного способа необязательной.

Далее, на этапе 8.2, для каждого значения задержек , , соответственно прямого и отраженного лучей получают три набора весовых коэффициентов, соответствующих векторам , , , и на этапе 8.3 производят вычисление трех взвешенных сумм компонентов вектора Х с этими весами:

где q=1, 2, 3 - номер вектора S, соответствующего паре задержек прямого и отраженного луча,

i, j - номера задержек прямого и отраженного лучей на сетке построения ФП.

После этапа 8.3 полученные значения взвешенных сумм , и подвергаются на этапе 8.5 попарному перемножению и суммированию с полученными на этапе 8.4 весами обратной матрицы R^ij=(S^ijTS^ij)^-1 размерности 3×3 для вычисления ФП:

Эта операция представляет из себя вычисление квадратичной формы.

Результатом вычислений является ФП {ε^ij}, сохраняемая в памяти на этапе 8.6. Эта процедура повторяется для каждой пары задержек прямого и отраженного лучей (каждой паре задержек , соответствуют свои значения векторов весовых коэффициентов S^ij и обратных матриц R^ij). После этого на этапе 8.7 производится нахождение и интерполирование глобального максимума по всем вычисленным значениям ФП {ε^ij} по параметрам задержек прямого и отраженного лучей , .

Область перебора задержек прямого и отраженного лучей определялась из анализа ошибок псевдодальности, рассчитанных для узкоапертурного коррелятора (Фиг.13). Вначале находилась задержка τ_max, соответствующая положению интерполированного максимума накопленных мощностей. При этом задержки прямого луча перебираются в диапазоне относительно τ_max:

,

где С_св - скорость света,

а задержки отраженного луча - в диапазоне, в котором отраженный луч оказывает влияние на точность оценки задержки прямого луча, а именно:

.

Моделирование показало, что для перебора задержки прямого луча требуется шаг 1-2 м/С_св, а для перебора задержки отраженного луча - (10-20 м)/С_св

Пример ФП для двухлучевого сигнала приводится на Фиг.10, 11.

Для получения оценок задержек приходящих по прямому и отраженному лучам сигналов , использовалась двухмерная параболическая аппроксимация максимума ФП.

Для сопоставления точности предложенного метода с узкоапертурным коррелятором и стробовым коррелятором в одинаковых условиях (ширина полосы частот сигналов приемника ΔF=6 MHz, ослабление сигнала, приходящего по отраженному лучу, равное 6 дБ), было выполнено сравнительное моделирование, результаты которого представлены на Фиг.12-14.

Ошибки смещения измерения задержки сигнала, приходящего по прямому лучу, для предложенного метода, изображенные на Фиг.12, очень малы (меньше чем 0.12 м/С_св) по сравнению с узкоапертурным коррелятором (Фиг.13, ошибки смещения до 15 м/С_св) и стробовым коррелятором (Фиг.14, смещение до 7 м/ С_св).

Выше (Фиг.8) был описан способ уточнения коррекций с использованием векторов S=Q^-1/2P, X=Q^-1/2Z и обратных матриц (S^ijTS^ij)^-1. Недостатком этой схемы является необходимость хранения наряду с векторами S обратных матриц R=(S^TS)^-1 и вычисления квадратичных форм на этапе 8.5. Рассмотрим альтернативный способ уточнения коррекций - с использованием ортонормированных векторов сигналов, зависящих от задержек сигналов прямого и обратного лучей.

Матрица (S^TS) является симметричной неотрицательно определенной матрицей размерности 3×3. Эта матрица может быть представлена в виде:

где U - квадратная матрица ортонормированных собственных векторов размерности 3×3,

Λ=diag(λ₁,λ₂,λ₃) - диагон