Способ и устройство для проецирования двухмерных рисунков на сложные поверхности трехмерных объектов

Способ и устройство для проецирования двухмерных рисунков на сложные поверхности трехмерных объектов

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к декорированию трехмерных проектов и, в частности, к способу и устройству обеспечения моделирования декоративных элементов трехмерных объектов на основании двухмерного изображения этих декоративных элементов.

Проецирование двухмерного изображения на трехмерный объект часто используют во многих областях промышленности для декорирования этих объектов. Сложность этой проблемы зависит от характера трехмерного объекта и от характера поверхности проецирования. Так, если проецирование двухмерного изображения на сплошную поверхность небольших размеров, такую как наружная поверхность банки, не представляет особой трудности, то проецирование логотипа, символа или названия на наружную поверхность самолета создает многочисленные проблемы. В частности, сложность формы поверхности проецирования, фактор масштаба между воспроизводимым изображением и исходным изображением, а также наличие некоторых специальных элементов, на которых необходимо закрасить или не закрашивать некоторые части воспроизводимого изображения, такие как иллюминатор, могут усложнить поставленную задачу.

Как правило, целью декорирования самолетов является нанесение коммерческого логотипа авиакомпаний, и оно часто состоит в нанесении краской названий, знаков и логотипов, которое должно производиться идеально. Адаптация знака авиакомпании к особым формам каждого самолета, как правило, основана на опыте и эмпирическом анализе. Утверждение этой адаптации часто связано с выполнением макетов. Этот процесс характеризуется многими недостатками, в частности, что касается стоимости и сроков выполнения.

В европейском патенте ЕР 0593340 раскрыты способ и устройство обеспечения декорирования трехмерного объекта. Способ состоит в создании трехмерной модели декорируемого объекта с графическим изображением декоративного элемента. После этого на основании трехмерной модели на объекте локализуют, по меньшей мере, некоторые характерные точки графического изображения для позиционирования, например, адгезивных лент ограничения декоративного элемента, или трафаретов, или заранее вырезанных декоративных элементов и т.д. Настоящее изобретение применяется, в частности, для декорирования самолета логотипами, буквами или отличительными знаками на наружной поверхности этого самолета.

Хотя этот способ позволяет моделировать декоративные элементы, предназначенные для воспроизведения на самолете, преобразование двухмерного изображения в трехмерное изображение, адаптированное для поверхности самолета, осуществляют путем конусного проецирования по отношению к точкам визирования и путем адаптации проекции.

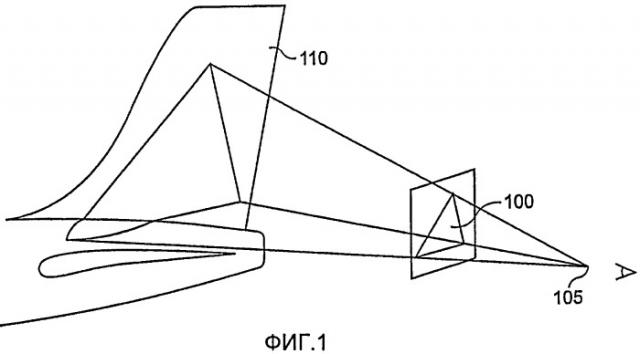
На фиг.1 показан пример конусного проецирования, позволяющего воспроизвести двухмерное изображение на наружной поверхности самолета. Проецирование изображения 100 из точки 105 проецирования на вертикальное оперение самолета 110 показывает проблемы, связанные с конусным проецированием на изменяющуюся часть наружной поверхности самолета, такую как сопряжение между вертикальным оперением и фюзеляжем.

Поэтому возникает необходимость в непосредственном получении проекции двухмерного изображения на трехмерном объекте со сложной поверхностью, не прибегая к адаптации, в частности, в зонах меняющейся формы.

Настоящее изобретение позволяет решить, по меньшей мере, одну из вышеуказанных проблем.

В связи с этим объектом изобретения является способ проецирования двухмерного рисунка на поверхность трехмерного объекта, при этом способ содержит следующие этапы:

- определяют, по меньшей мере, одну исходную кривую на двухмерном рисунке и, по меньшей мере, одну кривую проекции на поверхности трехмерного объекта, при этом исходная кривая и кривая проекции имеют, каждая, начальную точку;

- определяют, по меньшей мере, одно соотношение проекции;

- выбирают точку двухмерного рисунка;

- определяют, по меньшей мере, одну абсциссу проекции выбранной точки в зависимости от, по меньшей мере, одной абсциссы выбранной точки и от соотношения проекции;

- определяют ординату проекции выбранной точки в зависимости от ординаты выбранной точки и от соотношения проекции;

- определяют плоскость ординаты, содержащую точку кривой проекции, определенную абсциссой проекции выбранной точки; и

- определяют проекцию выбранной точки на поверхность трехмерного объекта в зависимости от ординаты проекции выбранной точки, пересечения поверхности трехмерного объекта с плоскостью ординаты и кривой проекции.

Таким образом, изобретение позволяет оптимизировать перенос двухмерного изображения на поверхность трехмерного объекта, сводя к минимуму искажения, связанные с изменением формы частей поверхности трехмерного объекта.

Предпочтительно используют второе соотношение для переноса двухмерного рисунка с соотношениями, разными для каждого направления.

Предпочтительно переносят также касательные к выбранным точкам, чтобы повысить качество переносимого изображения.

Согласно первому варианту выполнения плоскость ординаты является нормалью к кривой проекции.

Согласно второму варианту выполнения плоскость ординаты параллельна плоскости отсчета.

Согласно другому варианту выполнения плоскость ординаты образована второй точкой и заранее определенным направлением. Предпочтительно вторая точка является проекцией второй абсциссы точки, выбранной по второй исходной кривой. Предпочтительно ординату проекции выбранной точки определяют при помощи соотношения расстояний между выбранной точкой и точками двух исходных кривых, определенными двумя абсциссами выбранной точки.

Согласно частному варианту выполнения, по меньшей мере, одну из выбранных точек проецируют согласно одному из трех частных вариантов выполнения и, по меньшей мере, одну другую выбранную точку проецируют согласно другому частному варианту выполнения. Таким образом, проекцию двухмерного рисунка адаптируют к характеру поверхности трехмерного объекта.

Согласно еще одному частному варианту выполнения двухмерный рисунок можно трансформировать до проецирования на поверхность трехмерного объекта или во время проецирования. Таким образом, двухмерный рисунок можно адаптировать для специальных потребностей.

Трехмерный объект может быть реальным объектом или цифровым объектом, таким как модель, используемая в программе компьютерного проектирования.

Объектом настоящего изобретения является также устройство, содержащее средства, предназначенные для осуществления каждого из этапов описанного выше способа.

Объектом изобретения является также компьютерная программа, содержащая команды, предназначенные для осуществления каждого из этапов описанного выше способа.

Другие преимущества, задачи и отличительные признаки настоящего изобретения будут более очевидны из нижеследующего подробного описания со ссылками на прилагаемые чертежи, на которых:

фиг.1 - пример конусного проецирования, позволяющего воспроизводить двухмерное изображение на наружной поверхности самолета;

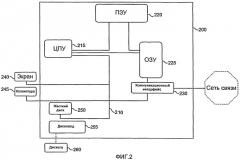
фиг.2 - пример прибора, позволяющего применять изобретение;

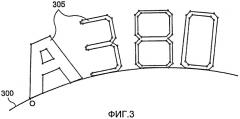
фиг.3 - пример двухмерного изображения, воспроизводимого на поверхности трехмерного объекта;

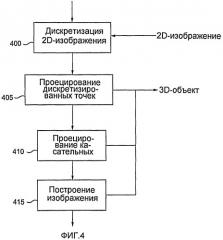
фиг.4 - некоторые общие этапы алгоритма проецирования двухмерного изображения на поверхность трехмерного объекта;

фиг.5 - позиционирование кривой проекции на поверхности трехмерного объекта, в данном случае вертикального оперения самолета;

фиг.6 - некоторые этапы алгоритма проецирования точек двухмерного изображения, воспроизводимого на поверхности двухмерного объекта согласно первому и второму вариантам выполнения;

фиг.7, в том числе фиг.7а и 7b, - пример проецирования точек двухмерного изображения на поверхность вертикального оперения самолета согласно первому и второму вариантам выполнения;

фиг.8 - пример двухмерного изображения, воспроизводимого на поверхности трехмерного объекта согласно третьему варианту выполнения;

фиг.9, в том числе фиг.9а и 9b, - пример проецирования точек двухмерного изображения на поверхность вертикального оперения самолета согласно третьему варианту выполнения;

фиг.10, в том числе фиг.10а и 10b, - иллюстрация механизма проецирования касательных.

Нижеследующее описание основано на примере наружного декорирования самолета, однако следует иметь в виду, что способ и устройства в соответствии с настоящим изобретением могут применяться для декорирования любых трехмерных объектом на основании двухмерного изображения декоративного элемента.

На фиг.2 показан пример прибора 200, выполненного с возможностью применения изобретения. Прибор 200 является, например, микрокомпьютером или рабочим постом, подключаемым или нет к сети связи. Прибор 200 содержит коммуникационную шину 210, с которой предпочтительно соединены:

- центральный блок 215 обработки, такой как микропроцессор, обозначенный ЦПУ (центральное процессорное устройство);

- постоянная память 220, которая может содержать программы для осуществления изобретения и обозначена ПЗУ (постоянное запоминающее устройство);

- оперативная память 225, которая после подачи напряжения содержит рабочую программу способа в соответствии с настоящим изобретением, а также регистры, выполненные с возможностью записи переменных и параметров, необходимых для осуществления изобретения, обозначенная ОЗУ (оперативное запоминающее устройство); и

- коммуникационный интерфейс 230, соединенный с сетью связи, при этом интерфейс выполнен с возможностью передачи и приема данных.

Факультативно прибор может также содержать следующие компоненты:

- экран 240, позволяющий просматривать данные и/или служить графическим интерфейсом для пользователя, который может задействовать программы в соответствии с настоящим изобретением при помощи клавиатуры 245, дополненной или нет любым другим средством, таким как устройство управления позицией курсора, такое как мышь, оптический карандаш или тактильный экран;

- жесткий диск 250 или запоминающее устройство, такое как флэш-карта, которое может содержать программы в соответствии с настоящим изобретением, а также данные, используемые или получаемые во время осуществления изобретения; и

- дисковод 255 для считывания с дискет (или с любого другого схемного носителя данных), выполненный с возможностью установки дискеты 260, и считывания с нее или записи на нее обработанных данных или данных, предназначенных для обработки в соответствии с настоящим изобретением.

Коммуникационная шина обеспечивает связь и взаимодействие между различными элементами, включенными в прибор 200 или соединенными с этим прибором. Использование шины не является ограничительным, и, в частности, центральный блок выполнен с возможностью передачи команд любому элементу прибора 200 напрямую или через другой элемент прибора 200.

Дискеты 260 можно заменить любым носителем информации, например, таким как компакт-диск (CD-ROM) с возможностью перезаписи или нет, диск ZIP или карта памяти, или, в целом, средство хранения информации, считываемое микрокомпьютером или микропроцессором, интегрированное в прибор или нет, в случае необходимости, съемное и выполненное с возможностью записи одной или нескольких программ, исполнение которых обеспечивает осуществление способа в соответствии с настоящим изобретением.

Рабочая программа, позволяющая прибору применять изобретение, может быть записана как в постоянной памяти 220, так и на жестком диске 250 или на съемном цифровом носителе, например, таком как описанная выше дискета 260. Согласно варианту рабочая программа может быть получена при помощи сети связи через интерфейс 230 и записана в запоминающие средства прибора 20, такие как жесткий диск 250, перед ее исполнением.

Центральный блок 215 выполнен с возможностью управления исполнением команд или частей рабочей программы для выполнения программы или программ в соответствии с настоящим изобретением, при этом команды записаны в одном из вышеуказанных запоминающих средств. Во время подачи напряжения программа или программы, которые записаны в энергонезависимом запоминающем устройстве, например на жестком диске 250 или в постоянной памяти 220, передаются в оперативную память 225, которая содержит рабочую программу для выполнения программ в соответствии с настоящим изобретением, а также регистры для записи переменных и параметров, необходимых для реализации изобретения.

Следует также отметить, что прибор, содержащий устройство в соответствии с настоящим изобретением, может быть также программируемым прибором. В этом случае прибор содержит рабочую программу исполнения компьютерных программ, например, внесенную в специализированную интегральную схему (Application Specific Integrated Curcuit или ASIC).

На фиг.3 показано двухмерное изображение, которое необходимо воспроизвести на поверхности трехмерного объекта, например оперения, показанного на фиг.1. Двухмерное изображение или исходное изображение содержит кривую 300 и начальную точку О, принадлежащую этой кривой. Кривая 300, в дальнейшем называемая исходной кривой, рассматривается как ось абсцисс системы координат, в которой определены точки, образующие изображение, предназначенное для воспроизведения на поверхности трехмерного объекта. Предпочтительно исходная кривая связана с воспроизводимым изображением, как показано на фиг.3, однако она может быть любой. В представленном примере воспроизводимое изображение содержит буквы «А380». Предпочтительно ось ординат выбирают таким образом, чтобы она была ортогональной к исходной кривой в рассматриваемой точке абсциссы.

Способ в соответствии с настоящим изобретением можно подразделить на четыре следующих этапа, показанные на фиг.4:

- дискретизация двухмерного изображения, предназначенного для воспроизведения на поверхности трехмерного объекта (этап 400);

- проецирование дискретизированных точек на поверхность трехмерного объекта (этап 405);

- проецирование касательных к дискретизированным точкам на поверхность трехмерного объекта (этап 410); и

- построение изображения на поверхности трехмерного объекта на основании проецированных точек и касательных (этап 415).

Следует отметить, что этап переноса касательных к дискретизированным точкам не является обязательным, но, как правило, позволяет повысить качество проецированного изображения.

Предпочтительно двухмерное исходное изображение состоит из кривых и точек. Точки можно проецировать одну за другой согласно процессу, представленному в описании ниже. Кривые, как правило, представляющие собой границу между двумя разными цветами, предпочтительно дискретизируют с определением погрешности хорды и максимального расстояния между двумя последовательными точками. Точки, полученные в результате дискретизации, а также, в случае необходимости, касательные к кривым в этих точках, проецируют или переносят на поверхность трехмерного объекта, чтобы реконструировать кривые путем сглаживания проецированных точек. Проецирование касательных при помощи этого же процесса позволяет произвести доводку проекции исходного изображения. Дискретизация может быть автоматической или нет.

Можно использовать другие способы дискретизации. Например, дискретизацию можно осуществлять таким образом, чтобы каждая дискретизированная точка соответствовала выделяющейся или особой точке исходного изображения. Точка считается выделяющейся или особой, если она соответствует экстремуму или если она характеризует разрыв кривизны, такой как резкое изменение направления.

Для большей ясности в дальнейшем тексте описания будем считать, что единицы координат эквивалентны по всем направлениям, то есть, в частности, что расстояние между началом координат и точкой с координатами (1,0) равно расстоянию между началом координат и точкой с координатами (0,1). Вместе с тем, можно использовать и другие единицы.

Для переноса дискретизированных точек двухмерного изображения на поверхность трехмерного объекта можно использовать несколько способов.

Согласно первому варианту выполнения кривую проекции определяют на поверхности трехмерного объекта. Эту кривую, содержащую начало координат О', используют в качестве оси отсчета для отображения абсциссы проекции дискретизированных точек исходного изображения на поверхности трехмерного объекта. Эта кривая проекции может быть подобной относительно исходной кривой, при этом она может быть подобной в другом масштабе или может быть другой. На фиг.5 показан самолет, на который нанесли кривую (500) проекции. Пример алгоритма согласно этому первому варианту выполнения схематично показан на фиг.6.

После определения кривой проекции на поверхности трехмерного объекта (этап 600) вычисляют соотношение длин исходной кривой (l) и кривой проекции (L) (этап 605). По умолчанию, соотношение высот исходного изображения и проецированного изображения равно соотношению исходной кривой и кривой проекции. Вместе с тем, пользователь может определить другое соотношение или ввести желаемую высоту проецируемого изображения, чтобы произвести вычисление соотношения высот исходного изображения (h) и проецируемого изображения (Н). Предпочтительно высотой Н является расстояние, измеренное на поверхности трехмерного объекта, а не вычисленное математическое расстояние в трехмерном пространстве. Если кривая проекции идентична исходной кривой, соотношение равно единице, и нет необходимости в его вычислении. В альтернативном варианте соотношение может определить пользователь. Выбирают (этап 610) точку исходного изображения, предпочтительно дискретизированную точку исходного изображения, имеющую координаты (x,y). После этого вычисляют (этап 615) абсциссу проекции этой точки. Предпочтительно абсциссу проекции выбранной точки определяют при помощи следующего отношения:

где x является абсциссой выбранной точки исходного изображения по исходной кривой, а x' является абсциссой проекции выбранной точки на трехмерном проекте по кривой проекции.

Соотношение L/l можно исключить, если соотношение равно 1, или можно заменить переменной, определенной пользователем.

Точно так же вычисляют ординату проекции выбранной точки (этап 620). Аналогично абсциссе, ординату проекции выбранной точки предпочтительно определяют при помощи следующего отношения:

или

где y является ординатой проекции выбранной точки исходного изображения, предпочтительно по прямой, ортогональной к исходной кривой в x, а y' является ординатой проекции выбранной точки на поверхности трехмерного объекта по пересечению плоскости ординаты с поверхностью трехмерного объекта. По умолчанию, соотношение высот исходного изображения и проецируемого изображения равно соотношению длин исходных кривых и кривых проекции (H/h=L/l). Поэтому нет необходимости в систематическом определении высоты изображения, проецируемого на трехмерный объект. Соотношение тоже может быть определено пользователем.

Для проецируемой точки с абсциссой x' кривая ординат определяется пересечением плоскости проекции или плоскости ординат, проходящей через точку кривой проекции с абсциссой x', с поверхностью трехмерного объекта. Согласно этому первому варианту выполнения плоскость ординат определяют как нормаль к кривой проекции в x'.

Таким образом, для определения проекции выбранной точки необходимо перенести значение x' на кривую проекции от начала O', определить пересечение плоскости-нормали к кривой проекции в этой точке с поверхностью трехмерного объекта и перенести значение ординаты на кривую, образованную этим пересечением (этапы 625 и 630).

Отметив проекцию выбранной точки на трехмерном объекте, производят тест для того, чтобы определить, все ли точки, полученные в результате дискретизации, были проецированы (этап 635). Если были проецированы не все точки дискретизации, выбирают новую точку (этап 610) и повторяют этапы 615-635.

На фиг.7, включающей фиг.7а и 7b, показано проецирование точки исходного изображения, показанного на фиг.3, на вертикальное оперение по кривой проекции 500 согласно первому варианту выполнения. Фиг.7а воспроизводит часть фиг.3, на которой добавлены обозначения и координаты проецируемой точки. Как было указано выше, точка 700 имеет координаты (x,y) в системе координат, образованной исходной кривой и прямой, ортогональной к этой кривой в точке с абсциссой х. Фиг.7b воспроизводит часть фиг.5. После определения абсциссы x' проекции точки 700, как было указано выше, значение x' переносят на кривую проекции 500. Отмечают пересечение (710) плоскости (700), являющейся нормалью к этой кривой 500 в точке абсциссы x' этой кривой, с поверхностью трехмерного объекта, в данном случае вертикального оперения. Ординату y' проекции точки 700 переносят на кривую пересечения 710. Точка 715, имеющая координаты (x',y'), является проекцией точки 700 на поверхность трехмерного объекта.

Согласно второму варианту выполнения плоскость 705 ординаты определяют как плоскость, параллельную плоскости отсчета, причем эта плоскость, параллельная плоскости отсчета, проходит через точку абсциссы x' кривой проекции. Эту же плоскость отсчета используют для проецирования всех точек дискретизации или для части этих точек. Предпочтительно плоскость отсчета выбирают в зависимости от формы трехмерного объекта и направления текста, логотипа или символов, которые необходимо проецировать. Обычно плоскость отсчета является ортогональной или параллельной по отношению к оси фюзеляжа самолета.

Согласно третьему варианту выполнения плоскость ординат определяют двумя точками поверхности трехмерного объекта и заранее определенным направлением. Это направление может быть определено автоматически в соответствии с характером поверхности трехмерного объекта или может быть задано пользователем. Для этого на предназначенном для проецирования двухмерном изображении определяют две исходные кривые, например первую исходную кривую, связанную с минимальными значениями y, и вторую исходную кривую, связанную с максимальными значениями y. Каждая исходная кривая содержит начало (О₁ и О₂). Точно так же на поверхности трехмерного объекта определяют две кривые проекции. Каждая кривая проекции содержит начало (О₁' и О₂'). Предпочтительно эти две кривые являются нижней и верхней границами проекции двухмерного изображения на поверхность трехмерного объекта. На фиг.8 показаны некоторые этапы примера алгоритма согласно этому третьему варианту выполнения.

После определения двух кривых проекции на поверхности трехмерного объекта, на которую необходимо проецировать двухмерное изображение (этап 800), вычисляют (этап 805) соотношение длин первой исходной кривой (l₁) и первой кривой проекции (L₁) и соотношение длин второй исходной кривой (l₂) и второй кривой проекции (L₂). Выбирают (этап 810) точку исходного изображения, предпочтительно дискретизированную точку. После этого для каждой из двух кривых проекции вычисляют (этап 815) абсциссу проекции этой точки. Предпочтительно абсциссы проекций выбранной точки определяют при помощи следующих отношений:

;

где x₁ является абсциссой выбранной точки исходного изображения по первой исходной кривой, x₂ является абсциссой выбранной точки исходного изображения по второй исходной кривой, х₁' является абсциссой проекции выбранной точки на трехмерном объекте по первой исходной кривой, х₂' является абсциссой проекции выбранной точки на трехмерном объекте по первой исходной кривой, l₁ является длиной первой исходной кривой, l₂ является длиной второй исходной кривой, L₁ является длиной первой кривой проекции и L₂ является длиной второй кривой проекции.

Предпочтительно абсциссу х₁ определяют как ортогональную проекцию выбранной точки на первой исходной кривой (как в первом и втором вариантах выполнения). Предпочтительно абсциссу х₂ определяют пересечением прямой, проходящей через выбранную точку и через точку первой исходной кривой с абсциссой x₁, со второй кривой проекции.

Предпочтительно ординату выбранной точки определяют как соотношение расстояния между выбранной точкой и точкой первой исходной кривой с абсциссой х₁ и расстояния между точкой первой исходной кривой с абсциссой х₁ и точкой второй исходной кривой с абсциссой х₂. Таким образом, ординату выбранной точки можно выразить следующим отношением:

где Pt является выбранной точкой, Х₁ является точкой первой исходной кривой с абсциссой х₁ и Х₂ является точкой второй исходной кривой с абсциссой х₂.

Вычисляют (этап 820) ординату проекции выбранной точки. Предпочтительно ординату проекции выбранной точки определяют при помощи следующего отношения:

где y является ранее определенной ординатой выбранной точки, y' является ординатой проекции выбранной точки на трехмерном объекте по пересечению плоскости ординаты с трехмерным объектом, h является высотой исходного изображения и D является расстоянием между точками первой и второй кривых проекции соответственно с абсциссами x₁' и x₂' на поверхности трехмерного объекта. Таким образом, D выражает расстояние между этими точками по пересечению трехмерного объекта и плоскости-нормали к поверхности этого объекта, проходящей через точки первой и второй кривых проекции соответственно с абсциссами x₁' и x₂'. Следовательно значение y' выражает расстояние между точкой первой кривой проекции с абсциссой x₁' и проекцией выбранной точки на кривой ординат.

Для точки с абсциссой x₁' на первой кривой проекции и для точки с абсциссой x₂' на второй кривой проекции кривую ординат определяют пересечением плоскости ординат, проходящей через эти две точки и имеющей заранее определенное направление, с поверхностью трехмерного объекта.

Для определения проекции выбранной точки необходимо таким образом перенести значение x₁' на первую кривую проекции, перенести значение x₂' на вторую кривую проекции (в соответствии с начальными точками О₁' и О₂'), определить пересечение плоскости, проходящей через эти две точки, в заранее определенном направлении с поверхностью трехмерного объекта и перенести значение ординаты y' на кривую, образованную этим пересечением (этапы 825 и 830).

Отметив проекцию выбранной точки на поверхности трехмерного объекта, производят тест, чтобы определить, все ли дискретизированные точки были проецированы (этап 835). Если проецированы не все точки дискретизации, выбирают новую точку (этап 810) и повторяют этапы 815-835.

На фиг.9, включающей фиг.9а и 9b, показано проецирование точки исходного изображения, показанного на фиг.3, на вертикальное оперение по двум кривым проекции. Фиг.9а, как и фиг.7а, воспроизводит часть фиг.3, на которой добавлены обозначения и координаты предназначенной для проецирования точки. Как показано на фигуре, используют две исходные кривые (300-1 и 300-2). Выбранной точкой является точка 700, определенная значениями х₁, х₂ и y. На фиг.9а показаны две кривые проекции 900 и 905. После определения абсциссы x₁' проекции точки 700 по первой кривой проекции, как было указано выше, значение x₁' переносят на кривую проекцию 900 относительно начала координат О₁'. Точно так же после определения абсциссы x₂' проекции точки 700 по второй кривой проекции значение x₂' переносят на кривую проекцию 905 относительно начала координат О₂'. Отмечают пересечение (910) плоскости (915), проходящей через отмеченные точки x₁' и x₂' кривых проекции и имеющей заранее определенное направление, с поверхностью трехмерного объекта, в данном случае вертикального оперения. Ординату y' проекции точки 700 переносят на кривую, образованную пересечением 910. Точка 915 является проекцией точки 700 на поверхность трехмерного объекта согласно третьему варианту выполнения.

Выбор типа проецирования согласно первому, второму и третьему вариантам выполнения связан с типом проецируемого рисунка и с характером поверхности трехмерного объекта, на которую проецируют двухмерный рисунок.

Как было указано выше, предпочтительно осуществляют дополнительный этап переноса касательных. Согласно этому этапу для каждой дискретизированной точки исходного изображения предпочтительно проецируют, по меньшей мере, две касательные. Предпочтительно каждую касательную определяют точкой касательной, то есть дискретизированной точкой, и второй точкой, выбранной любым способом на касательной, предпочтительно вблизи дискретизированной точки. Проецирование этой второй точки согласно второму описанному выше способу позволяет построить проекцию касательной на поверхности трехмерного объекта, то есть построить проекцию исходного изображения.

На фиг.10, включающей фиг.10а и 10b, показан механизм проецирования касательных. На фиг.10а показана часть проецируемого исходного изображения, на котором выбрали дискретизированную точку (точка 1000). Точка 1000 имеет координаты (x,y). Касательные к исходному изображению в точке 1000 показаны в виде векторов 1005 и 1010. Точку с координатами (x₁,y₁) выбирают на векторе 1005, а точку с координатами (x₂,y₂) выбирают на векторе 1010. Проецирование точек с координатами (x,y), (x₁,y₁) и (x₂,y₂) согласно одному из описанных выше способов позволяет получить точки соответственно с координатами (x',y'), (x'₁,y'₁) и (x'₂,y'₂). Эти три последние точки позволяют построить векторы 1015 и 1020, соответствующие проекции соответственно векторов 1005 и 1010.

После проецирования точек и касательных можно построить проекцию исходного изображения путем соединения проецированных точки в соответствии с соединением дискретизированных точек и касательных. Это построение можно осуществить при помощи функции программы компьютерного проектирования, выполненной с возможностью соединения точек по определенным касательным.

Перед проецированием дискретизированных точек на поверхность трехмерного объекта или во время этого проецирования можно трансформировать исходное изображение. Так, можно использовать матрицу трансформации, чтобы, например, перевернуть исходное изображение горизонтально и/или вертикально. Можно также применять линейный или нелинейный фактор масштаба и, в целом, любые типы трансформации изображения.

Предпочтительно проецирование двухмерного изображения декоративного элемента на поверхность трехмерного объекта позволяет получить файл, содержащий координаты проекций точек двухмерного изображения декоративного элемента, а также характеристики этих точек. Среди этих характеристик можно указать, например, цвет, связанный с каждой точкой. Этот файл можно использовать для визуального отображения проекции на цифровой модели трехмерного объекта, например, применяя программу компьютерного проектирования. Файл можно также использовать для построения проекции непосредственно на реальном декорируемом трехмерном объекте.

Естественно, для удовлетворения специфических потребностей специалист в данной области может вносить в изобретение изменения.

1. Способ проецирования двухмерного рисунка на поверхность трехмерного объекта, отличающийся тем, что задают, по меньшей мере, одну исходную кривую на двухмерном рисунке и, по меньшей мере, одну кривую проекции (600, 800) на поверхности трехмерного объекта, при этом, по меньшей мере, одна исходная кривая и одна кривая проекции имеют, каждая, начальную точку (О, О₁, О₂, О', O₁', O₂'); определяют, по меньшей мере, одно соотношение проекции (605, 805); выбирают точку двухмерного рисунка (610, 810); определяют, по меньшей мере, одну абсциссу проекции выбранной точки, по меньшей мере, по одной абсциссе выбранной точки и, по меньшей мере, по одному соотношению проекции (615, 815); определяют ординату проекции выбранной точки в зависимости от ординаты выбранной точки и, по меньшей мере, от одного соотношения проекции (620, 820); определяют плоскость ординаты, содержащую точку, по меньшей мере, одной кривой проекции, определенную, по меньшей мере, одной абсциссой проекции выбранной точки; и определяют проекцию выбранной точки на поверхности трехмерного объекта в зависимости от ординаты проекции выбранной точки, пересечения поверхности трехмерного объекта с плоскостью ординаты и, по меньшей мере, одной кривой проекции (625, 825).

2. Способ по п.1, отличающийся тем, что ординату проекции выбранной точки определяют по ординате выбранной точки и второму соотношению проекции (605, 805).

3. Способ по п.1, отличающийся тем, что дополнительно содержит этап проецирования, по меньшей мере, одной касательной к двухмерному рисунку в выбранной точке на поверхность трехмерного объекта (410).

4. Способ по п.1, отличающийся тем, что плоскость ординаты является нормалью, по меньшей мере, к одной кривой проекции.

5. Способ по п.1, отличающийся тем, что плоскость ординаты параллельна плоскости отсчета.

6. Способ по п.1, отличающийся тем, что плоскость ординаты содержит проекцию абсциссы выбранной точки по второй кривой проекции, принадлежащей к поверхности трехмерного объекта, при этом плоскость ординаты определяется заданным направлением.

7. Способ по п.6, отличающийся тем, что выбранная точка задается двумя абсциссами по двум исходным кривым, причем проекция выбранной точки определяется двумя абсциссами по двум кривым проекции.

8. Способ по п.7, отличающийся тем, что ордината проекции выбранной точки определяется, в частности, соотношением расстояний между выбранной точкой и точками двух исходных кривых, определенными двумя абсциссами выбранной точки.

9. Способ проецирования двухмерного рисунка на поверхность трехмерного объекта, отличающийся тем, что, по меньшей мере, одну первую точку двухмерного рисунка проецируют на поверхность трехмерного объекта согласно способу по п.4, причем, по меньшей мере, одна вторая точка двухмерного рисунка проецируется на поверхность трехмерного объекта согласно способу по п.5.

10. Способ проецирования двухмерного рисунка на поверхность трехмерного объекта, отличающийся тем, что, по меньшей мере, одну первую точку двухмерного рисунка проецируют на поверхность трехмерного объекта согласно способу по п.5, и тем, что, по меньшей мере, одну вторую точку двухмерного рисунка проецируют на поверхность трехмерного объекта согласно способу по любому из пп.6, 7 и 8.

11. Способ по п.1, отличающийся тем, что дополнительно содержит этап трансформации двухмерного рисунка.

12. Способ по п.1, отличающийся тем, что трехмерный объект является цифровым объектом или реальным объектом.

13. Устройство, содержащее средства, выполненные с возможностью осуществления каждого из этапов способа по любому из пп.1-12.