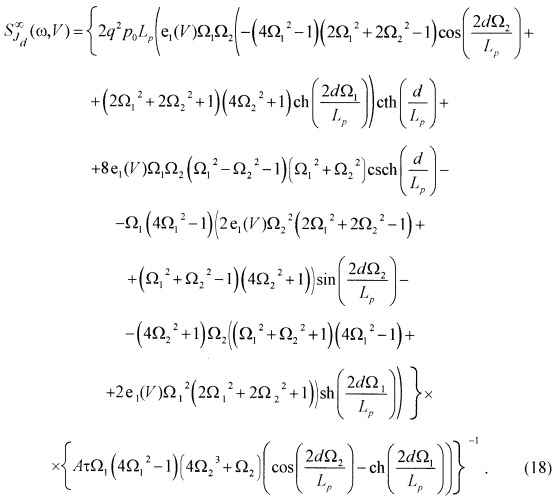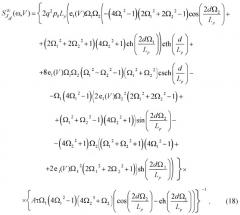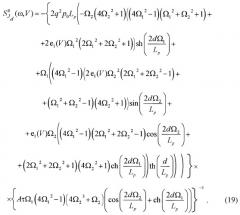Способ снижения спектральной плотности флуктуаций диффузионного тока фотодиода в области высоких частот

Способ снижения спектральной плотности флуктуаций диффузионного тока фотодиода в области высоких частот

Иллюстрации

Показать все

Реферат

Изобретение относится к фотоэлектронике и может использоваться в пороговых фотоприемных устройствах для регистрации коротких импульсов (∆t < τ, где ∆t - длительность импульса, τ - время жизни неравновесных носителей заряда в базе фотодиода) электромагнитного излучения оптического и инфракрасного диапазона.

Флуктуации темнового тока и фототока являются фундаментальными факторами, ограничивающими пороговые характеристики и рабочую температуру ИК фотодетекторов. Темновой ток HgCdTe фотодиодов дальнего ИК диапазона при криогенных температурах, а также фотодиодов среднего ИК диапазона, работающих при повышенных температурах, определяется диффузионным механизмом. При этом диффузионный ток p - n переходов с короткой базой (d < L, где d - толщина базы, а L - диффузионная длина неосновных носителей заряда) существенным образом зависит от типа контакта (граничного условия) к базе. Так, в известном способе [1] при диффузионный ток p - n перехода с короткой базой и блокирующим контактом в d/L раз меньше диффузионного тока аналогичного p - n перехода с длинной базой. Однако использование блокирующего контакта для снижения спектральной плотности флуктуаций (СПФ) диффузионного тока доказано в известном способе снижения спектральной плотности флуктуаций диффузионного тока фотодиода [1], принятом в качестве прототипа, только для области низких частот (ωτ << 1, где ω - круговая частота модуляции излучения). Точный расчет СПФ диффузионного тока p - n переходов с короткой базой в широком частотном диапазоне на основе метода Ланжевена выполнен только в настоящее время в работе [2].

Задачей предлагаемого изобретения является увеличение отношения сигнал/шум фотодиодов в области высоких частот (ωτ > 1) за счет снижения спектральной плотности флуктуаций диффузионного тока.

Технический результат достигается тем, что предложен способ снижения спектральной плотности флуктуаций диффузионного тока фотодиода в области высоких частот, заключающийся в том, что на p - n переход с короткой базой (d < L, где d - толщина базы, а L - диффузионная длина неосновных носителей в базе) и блокирующим контактом к базе подают обратное смещение V, удовлетворяющее условиям

3kT < q|V| < V _b,t и 3kT < q|V| < V _b,a,

где k - постоянная Больцмана;

T - температура;

q - заряд электрона;

V _b,t - напряжение туннельного пробоя;

V _b,a - напряжение лавинного пробоя.

Предложенное изобретение поясняется расчетами и графиками зависимостей.

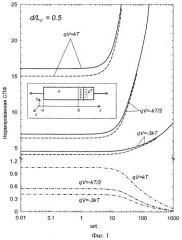
На Фиг.1 показана СПФ диффузионного тока p ⁺ - n перехода с базой конечной длины и омическим контактом к n области. Сплошные линии соответствуют нормированным СПФ диффузионного тока, пунктирные - нормированным аддитивным составляющим СПФ диффузионного тока, обусловленным случайным характером процессов рассеяния, штрихпунктирные - нормированным аддитивным составляющим СПФ диффузионного тока, обусловленным случайным характером процессов тепловой генерации и рекомбинации. Нормирующая величина , отношение d/L _p = 0.5. На врезке изображена структура рассматриваемого p ⁺ - n перехода.

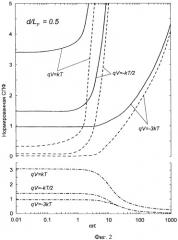
На Фиг.2 показана СПФ диффузионного тока p ⁺ - n перехода с базой конечной длины и блокирующим контактом к n области. Сплошные линии соответствуют нормированным СПФ диффузионного тока, пунктирные - нормированным аддитивным составляющим СПФ диффузионного тока, обусловленным случайным характером процессов рассеяния, штрихпунктирные - нормированным аддитивным составляющим СПФ диффузионного тока, обусловленным случайным характером процессов тепловой генерации и рекомбинации. Нормирующая величина, отношение d/L _p = 0.5.

На Фиг. 3 показана СПФ диффузионного тока обратносмещенного () p ⁺ - n перехода с длинной базой. Сплошная линия соответствует нормированной СПФ диффузионного тока, пунктирная - нормированная аддитивная составляющая СПФ диффузионного тока, обусловленная случайным характером процессов рассеяния, штрихпунктирная - нормированная аддитивная составляющая СПФ диффузионного тока, обусловленная случайным характером процессов тепловой генерации и рекомбинации. Нормирующая величина .

На Фиг. 4 показана СПФ диффузионного тока p ⁺ - n переходов с различной структурой: СПФ диффузионного тока p ⁺ - n перехода с базой конечной длины и омическим контактом к n области, СПФ диффузионного тока p ⁺ - n перехода с длинной базой, СПФ диффузионного тока p ⁺ - n перехода с базой конечной длины и блокирующим контактом к n области. Сплошные линии соответствуют нормированным СПФ диффузионного тока, пунктирные - нормированным аддитивным составляющим СПФ диффузионного тока, обусловленным случайным характером процессов рассеяния, штрихпунктирные - нормированным аддитивным составляющим СПФ диффузионного тока, обусловленным случайным характером процессов тепловой генерации и рекомбинации. Нормирующая величина , отношение d/L _p = 0.5, V = 0.

Рассчитаем СПФ диффузионного тока p - n перехода с короткой базой для случая омического и блокирующего контакта к базе при небольших смещениях любой полярности методом Ланжевена. Первоначально проведем анализ стационарной модели. Рассмотрим - n переход, темновой ток которого определяется процессами тепловой генерации и рекомбинации в квазинейтральной n области и на котором поддерживается небольшое постоянное смещение произвольной полярности (прямое или обратное) фиг. 1. Подобной структурой обладают p - n переходы на основе HgCdTe, выращенные молекулярно-лучевой эпитаксией [3], а также изготовленные низкоэнергетичной ионной обработкой [4]. Мы будем рассматривать случай, когда при прямом смещении - n перехода, а также при воздействии падающего излучения выполняется приближение низкого уровня инжекции. Заметим, что в данном приближении рекомбинацию дырок в n области можно рассматривать в рамках линейной модели, а модуляцией проводимости n области можно пренебречь.

Вместе с тем, мы ограничимся анализом случая не слишком больших обратных смещений рассматриваемого - n перехода, при которых можно пренебречь межзонным туннельным током и током, обусловленным туннелированием через ловушки, а также процессами ударной ионизации, т.е. будем считать что выполняются условия q|V| < V _b,t и q|V| < V _b,a, где V _b,t - напряжение туннельного пробоя, V _b,a - напряжение лавинного пробоя. Мы будем полагать пренебрежимо малым внутреннее сопротивление источника постоянного напряжения на диоде, т.е. будем считать внешнюю цепь диода короткозамкнутой. Также мы будем считать пренебрежимо малыми последовательное сопротивление n области, что позволяет не учитывать в дальнейшем ограничения частотных характеристик - n перехода. Мы будем рассматривать ситуацию, когда на p - n переход падает монохроматическое излучение со стороны области, и при этом сделаем допущение, что отражением от поверхности p - n перехода можно пренебречь. Мы также предположим, что толщина p области, равно как и толщина области пространственного заряда (ОПЗ) крайне малы, вследствие чего поглощением излучения в этих областях можно пренебречь.

Направим ось x от n области, толщина которой равна d, к области, а точку расположим на границе раздела квазинейтральной n области и ОПЗ (см. врезку на фиг. 1). Мы будем рассматривать случаи короткой где - диффузионная длина дырок в n области, τ - время жизни дырок в n области, - коэффициент диффузии дырок) и длинной () базы, а также два типа контакта (граничного условия) в точке - омический и блокирующий. Для расчета стационарной концентрации дырок в квазинейтральной n области рассматриваемого - n перехода необходимо решить уравнение непрерывности в амбиполярной форме, которое, при использовании допущения о линейной модели рекомбинации, имеет вид

,

где - концентрация неравновесных дырок в n области,

- концентрация равновесных дырок в n области,

- коэффициент поглощения,

- плотность потока фотонов падающего излучения.

В случае омического контакта граничное условие к уравнению (1) в точке имеет вид , а в случае блокирующего контакта граничное условие в данной точке имеет вид .

В точке граничное условие к уравнению (1) имеет вид [5],

где .

Распределение концентрации дырок в квазинейтральной n области и плотность суммарного тока рассматриваемого - n перехода и , соответственно, для случая омического контакта к n области, а также и , соответственно, для случая блокирующего контакта к n области, могут быть представлены в виде суммы двух слагаемых

Первые слагаемые данных уравнений определяются процессами тепловой генерации и рекомбинации в квазинейтральной n области в отсутствие засветки , , , и определяются выражениями

(2)

(3)

(4)

(5)

где . Отметим, что величины и представляют собой плотности диффузионного тока рассматриваемого - n перехода для случая омического и блокирующего контакта к n области соответственно.

Вторые слагаемые выражений для и обусловлены воздействием падающего излучения и определяются выражениями

(6)

(7)

(8)

(9)

Величины и представляют собой плотности фототока рассматриваемого - n перехода для случая омического и блокирующего контакта к n области соответственно. Расчеты показывают, что в точке существуют конечные пределы выражений (7) и (9). При выражения (7) и (9) переходят в известную формулу для плотности фототока p - n перехода с длинной базой , где - квантовая эффективность фотодиода [1, 6].

Рассмотрим теперь стохастическую модель. В рамках сделанных допущений при анализе флуктуационных явлений в рассматриваемом - n переходе можно ограничиться решением уравнения Ланжевена в амбиполярной форме. Процедура формального вывода такого уравнения [7] аналогична процедуре вывода детерминированного уравнения непрерывности в амбиполярной форме. В рассматриваемом случае квазинейтральной области уравнение Ланжевена в амбиполярной форме имеет вид

где - Фурье трансформанта флуктуации концентрации дырок,

- круговая частота,

- кинетическая диффузионная длина дырок в n области,

i - мнимая единица,

- Фурье трансформанта случайного источника, соответствующего случайному характеру процесса тепловой генерации и процесса рекомбинации,

- Фурье трансформанта случайного источника, соответствующего случайному характеру процесса фотогенерации,

- Фурье трансформанта случайного источника, соответствующего случайному характеру процессов рассеяния.

Отметим, что анализ флуктуаций в омическом резисторе в случае, когда принимается во внимание только случайный источник, соответствующий случайному характеру процессов рассеяния, приводит к известной формуле Найквиста для теплового шума [7].

В случае омического контакта (бесконечной скорости поверхностной рекомбинации) в точке концентрация неравновесных носителей в данной точке равна нулю, что справедливо как в детерминированном случае, так и в случае флуктуаций. Поэтому в случае омического контакта, стохастическое граничное условие имеет вид . Заметим, что предположение о нулевой скорости поверхностной рекомбинации в точке означает отсутствие поверхностного случайного источника, обусловленного случайным характером процессов тепловой генерации и рекомбинации в данной точке. Поэтому в случае блокирующего контакта (нулевой скорости поверхностной рекомбинации) в точке флуктуации дырочного тока в данной точке равны нулю . Мы также будем считать, что в точке отсутствует поверхностное рассеяние, а следовательно, отсутствует поверхностный случайный источник, обусловленный случайным характером процессов рассеяния.

Таким образом, в случае блокирующего контакта в точке флуктуация дырочного тока и флуктуация концентрации дырок в данной точке связаны соотношением , а стохастическое граничное условие имеет вид . Отметим, что в точке стационарные и стохастические граничные условия по форме совпадают.

Обоснуем теперь постановку граничного условия в точке . В случае, когда на - n переходе поддерживается обратное смещение, удовлетворяющее условию , ток во внешней цепи такого - n перехода определяется процессами тепловой генерации и фотогенерации в квазинейтральной n области. При этом электронно-дырочные пары, образовавшиеся в квазинейтральной n области и достигшие границы раздела с ОПЗ, быстро разделяются электрическим полем. Таким образом, в рассматриваемом случае обратносмещенного - n перехода в точке можно поставить стохастическое граничное условие [8], справедливое в диапазоне частот , где - время пролета дырок через ОПЗ, обусловленного дрейфом в электрическом поле - n перехода. В Приложении I работы [2] показано, что для - n перехода на основе тройного твердого раствора Hg_1-xCd_xTe (), сформированного низкоэнергетичной ионной обработкой [4], справедлива оценка с. Заметим, что быстрое разделение электронно-дырочных пар, образовавшихся в n области вследствие процессов тепловой генерации и фотогенерации и достигших границы раздела с ОПЗ, также будет иметь место в случае, когда к - n переходу приложено небольшое прямое или малое обратное смещение. Причем оценка времени пролета дырок через ОПЗ, обусловленного дрейфом в электрическом поле - n перехода, данная в Приложении I работы [2], в этом случае также сохранит свою справедливость.

В случае, когда к p ⁺ - n переходу приложено небольшое прямое или обратное смещение, дырки, диффундирующие из p ⁺ области, могут преодолеть потенциальный барьер в ОПЗ и попасть в n область. Согласно теории p - n перехода, разработанной Шокли [9], при не очень больших прямых и обратных смещениях, через ОПЗ рассматриваемого p ⁺ - n перехода протекают два встречных дырочных тока - диффузионный и дрейфовый, существенно, на несколько порядков, превышающих ток во внешней цепи p ⁺ - n перехода. Поток дырок, проходящих в n область и, следовательно, ток во внешней цепи прямосмещенного p ⁺ - n перехода существенно меньше потока дырок, диффундирующих из p ⁺ области, поскольку лимитируется рекомбинацией в n области.

Таким образом, на границе раздела ОПЗ - квазинейтральная n область вместо продиффундировавшей вглубь n области дырки практически мгновенно возникает новая, и концентрация дырок остается постоянной. Из сказанного следует, что в случае прямосмещенного p ⁺ - n перехода, а также в случае малого обратного смещения в точке можно поставить стохастическое граничное условие , справедливое в диапазоне частот , где - время пролета через ОПЗ дырок, диффундирующих из p ⁺ области p ⁺ - n перехода.

В Приложении II работы [2] показано, что в рассматриваемом случае небольших прямых и малых обратных смещений, для времени пролета через ОПЗ дырок, диффундирующих из p ⁺ области p ⁺ - n перехода, справедлива та же самая оценка, что и для времени пролета дырок через ОПЗ, обусловленного дрейфом в электрическом поле p ⁺ - n перехода, т.е .

Таким образом, при небольших прямых и обратных смещениях в достаточно широком частотном диапазоне в точке справедливо стохастическое граничное условие . Отметим, что в точке стационарные и стохастические граничные условия не совпадают по форме, причем стохастическое граничное условие не зависит от приложенного напряжения

Решение уравнения (10) для случая омического и блокирующего контакта и соответственно, находится легко. В квазинейтральной n области Фурье трансформанта флуктуации плотности дырочного тока определяется уравнением

[7].

Подставим в него решения уравнения (10) и рассчитаем значения Фурье трансформант соответствующих плотностей дырочного тока и . Затем, положив , получим выражения для Фурье трансформант флуктуации плотности суммарного тока p ⁺ - n перехода с базой конечной длины, к которому приложено небольшое смещение произвольной полярности и находящегося под воздействием падающего излучения, для случая омического и блокирующего контакта и соответственно

(11)

(12)

Рассчитаем теперь СПФ диффузионного тока. Флуктуации суммарного тока рассматриваемого - n перехода представляют собой стационарный случайный процесс, спектральная плотность флуктуаций (СПФ) которого связана с Фурье трансформантами флуктуаций соотношением [10]

(13)

где означает комплексное сопряжение,

- усреднение по ансамблю,

- дельта-функцию.

Случайные источники , и представляют собой дельта-коррелированные по пространственным координатам неоднородные стационарные случайные поля. Таким образом, для Фурье трансформант случайных источников , и и соответствующих взаимных СПФ , и справедливы соотношения, аналогичные уравнению (13). При этом взаимные СПФ случайных источников, соответствующих случайному характеру процессов тепловой генерации и рекомбинации, фотогенерации, а также рассеяния соответственно равны [7, 8]

(14)

(15)

(16)

Отметим, что в выражениях (14) - (16) фигурируют взаимные СПФ, определенные по положительным частотам ,

что имеет смысл, поскольку действительная часть взаимной СПФ стационарно связанных действительных случайных процессов является четной функцией частоты [11]. Последнее справедливо также и для СПФ действительных случайных процессов [10]. Поэтому в дальнейшем мы будем рассматривать только положительные частоты и определим СПФ суммарного тока на положительных частотах соотношением . Заметим также, что случайные источники , и не коррелированны между собой.

Уравнение (13), а также соотношения (11), (12), (14) - (16), (2), (4), (6), (8) после несложных, но довольно громоздких преобразований, выполненных при помощи программ компьютерной алгебры, позволяют рассчитать СПФ суммарного тока рассматриваемого - n перехода. При этом правая и левая части уравнения (13) после подстановки в него соотношений (11), (14) - (16), (2), (6), для случая омического контакта, либо (12), (14) - (16), (4), (8), для случая блокирующего контакта, должны быть усреднены по площади p - n перехода A.

Поскольку случайные источники и не коррелированны, СПФ суммарного тока будет включать в себя три аддитивных составляющих ,

первая из которых обусловлена случайным источником , т.е. случайным характером процессов тепловой генерации и рекомбинации, вторая обусловлена случайным источником , т.е. случайным характером процессов фотогенерации, а третья - случайным источником , т.е. случайным характером процессов рассеяния. При этом вследствие линейности рассматриваемой модели аддитивные составляющие СПФ суммарного тока и будут включать в себя слагаемые, обусловленные флуктуационными процессами, не зависящими от засветки (темновыми шумами) и соответственно, а также слагаемые, обусловленные фотоиндуцированными флуктуационными процессами и соответственно, т.е. , .

Аддитивная составляющая СПФ суммарного тока обусловлена исключительно флуктуациями процесса фотогенерации (см. уравнение (15)). Таким образом, СПФ суммарного тока рассматриваемого - n перехода можно записать в виде суммы двух величин

(17)

где величина обусловлена темновыми шумами и представляет собой СПФ диффузионного тока, а величина обусловлена фотоиндуцированными шумами и представляет собой СПФ фототока.

СПФ диффузионного тока рассматриваемого - n перехода с короткой базой для случая омического и блокирующего контакта к n области и соответственно определяется выражениями

Частотно зависимые величины и в формулах (24) - (29) определяются выражениями

(20)

(21)

Из формул (20) и (21) следует, что в рассматриваемом случае величины и удовлетворяют неравенствам и соответственно, т.е. точки и , в которых выражения (18), (19) имеют особенности, лежат вне области допустимых значений. Отметим, что при () существуют конечные пределы выражений (18), (19).

Выражения для аддитивных составляющих СПФ диффузионного тока - n перехода с базой конечной длины, обусловленных случайным характером процессов тепловой генерации и рекомбинации, а также случайным характером процессов рассеяния, для случая омического и блокирующего контакта к базе и , а также и соответственно, очень громоздки, поэтому мы ограничимся исследованием предельных значений этих СПФ.

Рассчитаем теперь значения аддитивных составляющих СПФ диффузионного тока - n перехода с длинной базой, обусловленных случайным характером процессов тепловой генерации и рекомбинации , а также рассеяния .

Результаты имеют вид

(22)

(23)

Из уравнений (22) и (23) следует, что в области применимости полученных результатов СПФ диффузионного тока рассматриваемого p ⁺ - n перехода с длинной базой определяется выражением

(24)

Легко можно проверить, что выражение (24) находится в полном соответствии с выражением для спектральной плотности шума идеального диода, полученным в монографии [11] методами теории случайных импульсов. Таким образом, выражение (24) представляет собой одну из форм записи известной формулы ван-дер-Зила для полных шумов идеального диода [11].

В случае обратного смещения, удовлетворяющего условию , когда можно положить , выражения (18) и (19) принимают вид

Из формул (25) и (26) следует, что в диапазоне частот, удовлетворяющем условию применимости стохастических граничных условий, СПФ диффузионного тока обратносмещенного p - n перехода с базой конечной длины и в случае омического, и в случае блокирующего контакта к базе не зависит от частоты и определяется формулой Шоттки.

Рассчитаем высокочастотные пределы аддитивных составляющих СПФ диффузионного тока - n перехода с базой конечной длины, обусловленных случайным характером процессов тепловой генерации и рекомбинации, для случая омического и блокирующего контакта к базе соответственно и . В случае малого обратного смещения, когда выполняется неравенство , а также в случае нулевого и прямого смещения в диапазоне частот конечных высокочастотных пределов аддитивных составляющих СПФ диффузионного тока - n перехода с базой конечной длины, обусловленных случайным характером процессов рассеяния, для случая омического и блокирующего контакта к базе не существует: и .

При этом легко можно показать, что при рассматриваемых смещениях и .

Конечные высокочастотные пределы аддитивных составляющих СПФ диффузионного тока - n перехода с базой конечной длины, обусловленных случайным характером процессов рассеяния, в диапазоне частот , для случая омического и блокирующего контакта к базе существуют только в случае обратного смещения, удовлетворяющего условию , когда можно положить , и определяются выражениями

Таким образом, на высоких частотах шумы диффузионного тока рассматриваемого p ⁺ - n перехода обусловлены случайным характером процессов рассеяния вне зависимости от приложенного напряжения и при любой структуре p ⁺ - n перехода.

Один из возможных способов повышения пороговых характеристик ИК фотодиодов на основе состава x≃0.2 состоит в использовании эффекта подавления диффузионного тока в p - n переходах с короткой базой и блокирующим контактом [1]. Из формул (25) и (26) видно, что при обратном смещении, удовлетворяющем условию , СПФ диффузионного тока рассматриваемого - n перехода с короткой базой определяется формулой Шоттки, т.е. в широком частотном диапазоне , СПФ