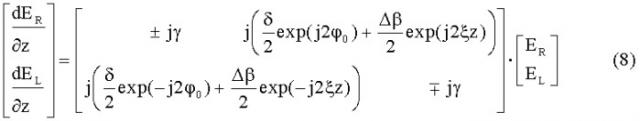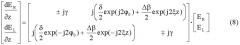Чувствительный элемент волоконно-оптического интерферометрического датчика электрического тока и магнитного поля

Чувствительный элемент волоконно-оптического интерферометрического датчика электрического тока и магнитного поля

Иллюстрации

Показать все

Реферат

Изобретение относится к волоконной оптике, в частности к волоконно-оптическим интерферометрическим датчикам, используемым для точного измерения электрического тока или магнитного поля. Датчик работает на основе эффекта Фарадея, в котором магнитное поле, направленное вдоль оптического пути в чувствительном элементе, вызывает разные скорости распространения у двух волн различных циркулярных поляризаций - левой и правой. Разница в скоростях приводит к накоплению фазовой задержки между указанными циркулярными волнами при распространении их по оптическому пути в чувствительном элементе, которая регистрируется с помощью указанного интерферометра. Датчик, например, [1] включает расположенные вдоль оптического пути источник оптического излучения, ответвители, фотодетектор, поляризатор, модулятор, линию задержки, четвертьволновую пластинку, чувствительный элемент, выполненный из оптического волокна, чувствительного к магнитному полю, и зеркало на конце этого волокна.

В указанном чувствительном элементе не могут быть использованы обычные оптические волокна (например, связные) или волокна с сильным линейным двойным лучепреломлением, сохраняющие линейную поляризацию - в них указанная фазовая задержка не накапливается, а применяются специальные волокна с собственным внутренним линейным двойным лучепреломлением и имеющим структуру с периодически повторяющимися вдоль оптического волокна оптическими параметрами.

Важной проблемой в создании указанного волоконно-оптического датчика электрического тока является нестабильность результатов измерений при меняющейся температуре. Эта проблема частично решается в патенте [1], который рассматривается нами как аналог. В [1] предлагается использовать специальную обработку сигналов фотодетектора для компенсации температурных погрешностей, связанных с неточным изготовлением четвертьволновой пластинки и ориентируемых по азимуту сварок вдоль оптического пути от источника оптического излучения до чувствительного элемента. Температурные погрешности чувствительного элемента предлагаемая в [1] обработка сигналов не компенсирует.

В патенте [2], принимаемом нами как прототип, описывается чувствительный элемент, представляющий собой уложенный по окружности отрезок кварцевого волоконного световода с внутренним двойным лучепреломлением, имеющим структуру с периодически повторяющимися вдоль оптического волокна оптическими параметрами. Параметры чувствительного элемента, в частности, длину намотки волокна, выбирают, согласно патенту [2], из условия минимального влияния внешних токов или несоосности проводника с измеряемым током и чувствительного элемента на результаты измерения. Однако температурная нестабильность указанного чувствительного элемента предлагаемым выбором параметров не компенсируется.

Техническим результатом предлагаемого изобретения является уменьшение зависимости результатов измерений от температуры чувствительного элемента и, тем самым, повышение надежности измерений в широком диапазоне температур.

Указанный технический результат достигается тем, что в предлагаемом техническом решении чувствительный элемент волоконно-оптического интерферометрического датчика электрического тока и магнитного поля выполнен в виде уложенного по окружности отрезка кварцевого волоконного световода с внутренним линейным двойным лучепреломлением и имеющим структуру с периодически повторяющимися вдоль оптического волокна оптическими параметрами, причем указанная периодическая структура выполнена в виде спиральной структуры внутреннего линейного двойного лучепреломления, при этом шаг L_tw спирали, длина биений L_b внутреннего линейного двойного лучепреломления, температурный коэффициент α_b внутреннего линейного двойного лучепреломления, радиус R окружности уложенного отрезка волоконного световода, радиус r поперечного сечения волоконного световода, рабочая длина волны λ интерферометрического датчика и показатель преломления n_o(λ) световедущей оболочки волоконного световода выбраны из соотношения:

где М=373,42°С;

N=637,9°C.

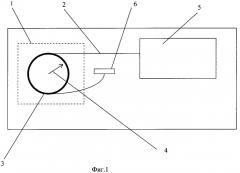
На фиг.1. показана схема чувствительного элемента и его подключение в схему датчика, где 1 - чувствительный элемент волоконно-оптического интерферометрического датчика электрического тока и магнитного поля; 2 - кварцевый волоконный световод; 3 - окружность, по которой уложен волоконный световод; 4 - радиус указанной окружности, равный R; 5 - схема обработки и регистрации оптического сигнала волоконно-оптического интерферометрического датчика электрического тока и магнитного поля; 6 - зеркало.

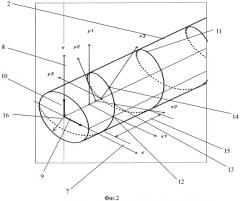
На фиг.2 показано внутреннее строение указанного кварцевого волоконного световода, где 7 и 8 - соответственно оси x и у линейного двойного лучепреломления волоконного световода; 9 - электрический вектор световой волны, ориентированный вдоль оси 7 (оси x); 10 - электрический вектор световой волны, ориентированный вдоль оси 8 (оси у); 11 - спиральная структура указанного линейного двойного лучепреломления; 12, 13, 14- точки выхода из световода осей х1, х2, х3 соответственно, располагающиеся по спирали 11; 15 - шаг указанной спиральной структуры 11, равный L_tw; 16 - радиус указанного поперечного сечения кварцевого волоконного световода 4, равный r.

На фиг.3 приведены зависимости относительной чувствительности S_отн интерферометрического датчика от отношения длины биений к шагу 15 спирали, равному L_b/L_tw, где 17 - указанная зависимость для случая прямолинейного волокна; 18 - для случая окружности 3 с радиусом 4, равным R=18,2 мм; 19 - для случая R=10 мм.

На фиг.4 приведены зависимости относительной чувствительности S_отн интерферометрического датчика от температуры для случая:

шаг 15 спирали равен L_tw=3 мм, длина биений L_b=9 мм, где 20 - прямолинейное волокно, 21 - радиус R=13 мм; 22 - радиус R=10 мм.

На фиг.5 приведены зависимости длины биений L_ind линейного двойного лучепреломления, индуцированного изгибом по радиусу 4 (R) при температурной зависимости относительной чувствительности S_отн, когда наклон графика равен наклону для прямолинейного волокна, где 23 - длина биений L_b=7 мм; 24 - длина биений L_b=12 мм; 25 - длина биений L_b=18 мм.

На фиг.6 приведены зависимости коэффициентов а и b (описывающих зависимости, приведенные на фиг.5) от длины биений L_b для различных значений температурного коэффициента α_b, где 26 - зависимость а(L_b) при α_b=0,00241 1/°С; 27 - зависимость b(L_b) при α_b=0,00241 1/°С; 28 - зависимость а(L_b) при α_b=0,001 1/°С; 29 - зависимость b(L_b) при α_b=0,001 1/°С, 30 - зависимость а(L_b) при α_b=0,0015 1/°С; 31 - зависимость b(L_b) при α_b=0,0015 1/°С.

На фиг.7 приведена иллюстрация линейной зависимости 32 а(L_b)/L_b, от α_b.

На фиг.8 приведена иллюстрация линейной зависимости 33 b(L_b)/L_b от α_b.

На фиг.9, примеры 1 и 2 иллюстрируются графиками зависимости относительной чувствительности S_отн интерферометрического датчика от температуры, где 35 - прямолинейное волокно; 34 - ромбики, радиус 4 равен R=15,7 мм; 37 - радиус 4 равен R=12 мм; 36 - треугольники, радиус 4 равен R=12,9 мм;

Техническое решение реализуется следующим образом.

Чувствительный элемент 1 волоконно-оптического интерферометрического датчика электрического тока и магнитного поля выполнен в виде отрезка кварцевого волоконного световода 2, уложенного по окружности 3 радиуса 4 и подключенного одним концом к схеме 5 обработки и регистрации оптического сигнала, а другим своим концом к зеркалу 6. Волоконный световод 2 с внутренним линейным двойным лучепреломлением имеет периодическую структуру, выполненную в виде спиральной структуры 11 указанного линейного двойного лучепреломления.

Спиральную структуру 11 указанного внутреннего линейного двойного лучепреломления с шагом 15 (L_tw) спирали выполняют при изготовлении волоконного световода путем, например, вращения заготовки с собственным внутренним линейным двойным лучепреломлением с угловой скоростью ω при непрерывной вытяжке волокна с линейной скоростью v. Температуру вытяжки, угловую скорость вращения ω и линейную скорость вытяжки v подбирают таким образом, чтобы образовалась спиральная структура 11 внутреннего двойного лучепреломления с заданным шагом 15 спирали, равным L_tw. На фиг.2 видно, как поворачиваются оси х и у указанного внутреннего линейного двойного лучепреломления, последовательно проходя положения 12, 13, 14.

Световое излучение проходит волоконный световод 2 чувствительного элемента 1 в прямом направлении от схемы 5 обработки и регистрации оптического сигнала до зеркала 6, потом отражается от зеркала и снова проходит световод 2 в обратном направлении. При таком прохождении компенсируются фазовые набеги между волнами ортогональных поляризаций, а (из-за инверсии этих волн на зеркале 6) разности фаз, обусловленные эффектом Фарадея, суммируются.

Линейный проводник с измеряемым током пропускают сквозь окружность 3 перпендикулярно чертежу фиг.1. Силовые линии магнитного поля тока располагаются по окружности и, следовательно, вдоль оси волоконного световода 2, уложенного по окружности 3. Оптический сигнал на указанной рабочей длине волны λ, пропорциональный измеряемому току или магнитному полю, получают как интерференционный сигнал двух волн ортогональных поляризаций, пропорциональный фазовой задержке dφ одной волны относительно другой, которая в свою очередь возникает в чувствительном элементе 1 (фиг.1) как следствие эффекта Фарадея (см., например, [3]):

где - индукция магнитного поля, V - константа Верде, - бесконечно малый элемент оптического волокна, чувствительного к магнитному полю, направленный вдоль его оси, dφ - фазовая задержка, приобретаемая на отрезке волокна dz.

Аксиальное магнитное поле в эффекте Фарадея вызывает скорость γ нарастания фазовой задержки на единице длины оптического волокна 2 между ортогональными циркулярными (левой и правой) волнами [3]:

где k₀=2π/λ - волновой вектор в пустоте, n_L·n_R - показатели преломления среды для левой и правой циркулярно поляризованных волн в присутствии магнитного поля, L_F - длина биений циркулярного двойного лучепреломления, возникающего в волокне 2 из-за эффекта Фарадея.

Указанное внутреннее линейное двойное лучепреломление вызывает скорость Δβ нарастания фазовой задержки на единице длины оптического волокна 2 между линейными ортогональными поляризованными волнами:

Изгиб по фиксированному радиусу 4, равному R, например, при намотке на катушку приводит к дополнительному линейному двойному лучепреломлению с длиной биений L_ind и скоростью δ нарастания фазовой задержки на единице длины оптического волокна [3]:

где длина биений L_ind связана с радиусом изгиба 4, равным R, соотношением [5]:

Наконец, скорость ξ, вращения главных осей 7 и 8 (фиг.2) указанного внутреннего линейного двойного лучепреломления на единице длины оптического волокна определяется через шаг 15 спирали 11, равный L_tw:

Поскольку с каждым шагом вдоль волоконного световода 2 поляризационные состояния оптического излучения встречают слегка повернутые оси указанного внутреннего линейного двойного лучепреломления, для описания эволюции поляризационных состояний требуется использовать дифференциальную матрицу Джонса, описывающую эволюцию поляризационных состояний бесконечно малыми шагами dz. В рамках вышеприведенных обозначений (2)-(7) эволюция поляризационных состояний при распространении световых волн ортогональных циркулярных поляризаций в указанном оптическом волокне 2, чувствительном к магнитному полю, осуществляется по известному соотношению (см., например, [4]) - дифференциальной матрице Джонса:

где E_R,E_L - напряженности электрического поля двух циркулярно поляризованных волн (вообще говоря, комплексные), j - мнимая единица, φ₀ - начальная фаза линейного двойного лучепреломления, индуцированного изгибом по радиусу R. Система дифференциальных уравнений (8) может быть решена в квадратурах только для прямолинейного волокна (δ=0), для остальных случаев общего решения нет - система уравнений (8) сводится к дифференциальному уравнению Рикатти с негармоническими коэффициентами. Расчет может быть выполнен на компьютере для фиксированных параметров. Результат вычисления - два вектора на комплексной плоскости: , , угол между направлениями которых есть искомая фазовая задержка Δφ. Отношение полученной фазовой задержки Δφ к фазовой задержке в идеальном волокне Δφ_ид=2VBz мы называем относительной чувствительностью S_отн:

Подчеркнем тот факт, что описание (8) эволюции поляризационных состояний относится к указанной спиральной структуре 11 указанного внутреннего линейного двойного лучепреломления с шагом 15 спирали, равным L_tw.

На фиг.3 приведены графики зависимости указанной относительной чувствительности S_отн от отношения L_b/L_tw при фиксированной величине длины биений L_b указанного внутреннего линейного двойного лучепреломления, рассчитанные по указанному рецепту (8)-(9). Графики отличаются радиусами 4 изгиба. Видно, что уменьшение радиуса 4 окружности 3, по которой уложено волокно 2 в чувствительном элементе 1, приводит к смене тенденции - рост указанной относительной чувствительности S_отн на графике 17 с увеличением отношения L_b/L_tw сменяется падением на графике 19. На этом принципиальном факте базируется предлагаемое техническое решение.

Причины температурной зависимости оптического сигнала на рабочей длине волны λ, пропорционального измеряемому току, от температуры чувствительного элемента следующие

1. Температурная зависимость диамагнитной константы Верде V в эффекте Фарадея в кварцевом оптическом волокне 2 согласно работе [5]:

где α_V=+6,9·10^-5 1/°C - температурный коэффициент константы Верде;

V₀=2,1 град/(Тл · см),

отсюда получаем зависимость указанной длины биений L_F от температуры:

2. Температурная зависимость указанной длины биений L_b внутреннего двойного лучепреломления:

где α_b=+(1÷2,8)·10^-3 1/°C - указанный температурный коэффициент внутреннего линейного двойного лучепреломления согласно работе [6].

Если зафиксировать указанную фазовую задержку в идеальном волокне Δφ_ид=2VBz при фиксированной температуре (например, при 0°С), то из-за вклада от константы Верде указанная относительная чувствительность S_отн будет возрастать с увеличением температуры. В случае использования прямолинейного волокна 2 (или уложенного по большому радиусу 4) в указанном чувствительном элементе 1 датчика к этой тенденции возрастания относительной чувствительности S_отн добавится возрастание чувствительности от увеличения длины биений L_b, согласно графику на фиг.3. В случае указанного чувствительного элемента 1 в виде волоконного световода 2, уложенного вокруг провода с измеряемым током по окружности 3 с фиксированным радиусом 4, равным R, и уменьшения этого радиуса, тенденция возрастания относительной чувствительности S_отн может смениться на тенденцию уменьшения S_отн. Можно подобрать такой радиус 4 изгиба волокна 2, при котором вклад от температурной зависимости константы Верде будет скомпенсирован вкладом от температурной зависимости длины биений L_b внутреннего двойного лучепреломления волокна. Однако, даже при изгибе по сравнительно большому радиусу 4, равному R, будет заметно сокращение зависимости указанного оптического сигнала от температуры по сравнению со случаем прямолинейного волокна, чувствительного к магнитному полю. Такое сокращение зависимости указанного оптического сигнала от температуры будет наблюдаться при уменьшении радиуса R вплоть до такого радиуса R_кр, при котором уменьшение относительной чувствительности S_отн при увеличении температуры станет преобладать над вкладом от возрастания константы Верде. Дальнейшее уменьшение радиуса изгиба приведет к увеличению зависимости указанного оптического сигнала от температуры, по сравнению со случаем прямолинейного волокна. Таким образом, следует определить радиус R_кр или связанную с ним длину биений L_{ind кр} и записать условие:

при выполнении которого, зависимость от температуры указанного оптического сигнала будет меньше, чем у прямолинейного волокна.

На фиг.4 приведены графики зависимостей относительных чувствительностей S_отн от температуры 20 - для прямолинейного волокна и 22 - для волокна уложенного по критическому радиусу R_кр, при котором отрицательный наклон графика совпадает по величине (но не по знаку) с наклоном графика для прямолинейного волокна. Длина биений L_b указанного внутреннего линейного двойного лучепреломления, его температурный коэффициент α_b и шаг 15 спирали 11, равный L_tw, фиксированы и равны соответственно L_b=9 мм, α_b=0,00241 1/°С и L_tw=3 мм. Величина критического радиуса R_кр или связанная с ним длина биений L_{ind кр} определяются подбором. Точно так же определяют указанные длины биений L_{ind кр} при других значениях длин биений L_b указанного внутреннего линейного двойного лучепреломления и шагах спирали L_tw. Полученные таким образом зависимости длины биений L_{ind кр} указанного дополнительного линейного двойного лучепреломления, наведенного изгибом от отношения L_b/L_tw, для различных длин биений L_b, указанного внутреннего линейного двойного лучепреломления приведены на фиг.5. Видно, что указанные зависимости почти линейные и что, чем больше указанная длина биений L_b, тем более круто растет L_{ind кр} при уменьшении шага спирали L_tw. Запишем указанную величину длины биений L_{ind кр} в виде:

при заданном значении L_b и получим зависимости а(L_b) и b(L_b), графики которых приведены на фиг.6 для трех значений указанного температурного коэффициента α_b указанного внутреннего линейного двойного лучепреломления: для α_b=0,00241 1/°С - функция а(L_b) (график 26 на фиг.6)

и функция b(L_b) (график 27 на фиг.6)

описываются формулами:

для α_b=0,0015 1/°С - функция а(L_b) (график 28 на фиг.6)

и функция b(L_b) (график 29 на фиг.6)

описываются формулами:

для α_b=0,001 1/°С - функция а(L_b) (график 30 на фиг.6)

и функция b(L_b) (график 31 на фиг.6)

описываются формулами:

Видно, что величины а(L_b) и b(L_b) линейно зависят от указанной длины биений L_b указанного внутреннего линейного двойного лучепреломления. Для трех значений указанного температурного коэффициента α_b можно подставить (15), (16) и (17) в выражение (14) и получить следующие равенства:

Видно, что величины a(L_b)/L_b и b(L_b)/L_b монотонно изменяются при уменьшении указанного температурного коэффициента α_b. На фиг.7 даны точками (квадратики) три значения величины а(L_b)/L_b как функции коэффициента α_b. Видно, что они лежат на одной прямой (график 32), проходящей через эти точки. На фиг.8 даны точками (треугольники) три значения величины b(L_b)/L_b как функции коэффициента α_b. Видно, что они лежат на одной прямой (график 33), проходящей через эти точки. График 32, описывается формулой:

а график 33 - формулой:

Подставив функции a(L_b) и b(L_b) из выражений (19) и (20) в формулу (14) получаем:

Коэффициенты при величине α_b имеют размерность°С. Подставив теперь величину L_ind из выражения (6) и величину L_{ind кр} из выражения (21) в неравенство (13), получим неравенство:

из которого, после простых алгебраических операций (деление левой и правой части на 22,792), получим формулу (1), которую было необходимо обосновать.

Пример 1. Чувствительный элемент 1 волоконно-оптического интерферометрического датчика тока и магнитного поля был выполнен в виде уложенного по окружности 3 отрезка кварцевого волоконного световода 2 радиусом r=62,5 мкм и показателем преломления световедущей оболочки n(λ)=1,444 на рабочей длине волны λ=1,55 мкм. Указанный кварцевый волоконный световод 2 имел внутреннее линейное двойное лучепреломление с длиной биений L_b=7 мм и температурным коэффициентом α_b=0,0015 1/°С, и периодическую структуру, выполненную в виде спиральной структуры 11 указанного линейного двойного лучепреломления с шагом 15 спирали 11, равным L_tw=2 мм. При радиусе 4 указанной окружности 3, равном R=15,7 мм, была получена минимальная зависимость относительной чувствительности S_отн от температуры. Расчет по формуле (1) дает неравенство:

которому вполне удовлетворяет найденное значение радиуса R=15,7 мм > 12,9 мм. На фиг.9 приведена полученная зависимость 34 (ромбики) относительной чувствительности S_отн от температуры вместе с теоретически рассчитанными зависимостями 35 - для прямолинейного световода и 36 - для волоконного световода 2, уложенного по окружности 3 радиусом 4, равным R=12,9 мм. Видно, что у волоконного световода, уложенного по окружности радиусом, равным 15,7 мм, относительная чувствительность S_отн существенно меньше зависит от температуры, чем у прямолинейного волокна.

Пример 2. Указанный чувствительный элемент по Примеру 1, отличающийся тем, что волоконный световод 2 был уложен по окружности 3 с радиусом 4, равным R=12 мм, не удовлетворяющим неравенству (1). Была получена зависимость 37 (фиг.9, треугольники) относительной чувствительности S_отн от температуры. Из чертежа видно, что наклон графика полученной зависимости больше, чем наклон графика 35 для прямолинейного световода.

Пример 3. Чувствительный элемент 1 волоконно-оптического интерферометрического датчика тока и магнитного поля должен быть выполнен в виде уложенного по окружности 3 большого радиуса 4 (равного R=50 мм) отрезка кварцевого волоконного световода 2 радиусом r=62,5 мкм с показателем преломления световедущей оболочки n(λ)=1,444 на рабочей длине волны λ=1,55 мкм. Указанный кварцевый волоконный световод 2 должен иметь фиксированное отношение длины биений внутреннего линейного двойного лучепреломления к шагу 15 указанной спиральной структуры 11, равное L_b/L_tw=3. Какой должна быть длина биений внутреннего линейного двойного лучепреломления, чтобы указанный чувствительный элемент 1 имел температурную зависимость относительной чувствительности S_отн не хуже, чем прямолинейный волоконный световод?

Непосредственный расчет по формуле (1) приводит к соотношению:

Полученная подбором (с минимизацией зависимости относительной чувствительности S_отн от температуры) величина L_b=75 мм удовлетворяет приведенному неравенству (1).

Таким образом, приведенные выше примеры показывают, что предлагаемое изобретение позволяет снизить зависимость результатов измерений волоконно-оптическим интерферометрическим датчиком электрического тока и магнитного поля от температуры.

Литература

1. Патент США №5696858, Blake J.N., «Fiber optics apparatus and method for accurate current sensing», 09.12.1997.

2. Патент США №6356351, Blake J.N., «Fiber-optic current sensor with improved isolation», 12.03.2002.

3. Rashleigh S.C., J.Lightwave Technol. (1983), v.1, p.312.

4. Губин В.П., Исаев В.А., Моршнев С.К. и др. Квантовая электрон., (2006), т.36, №3, с.287.

5. Williams O.A., Rose A.H., Day G.W. et al, Appl. Opt. (1991), V.30, №10, p.1176.

6. Zhang F, Lit J.W.Y, Appl. Opt, (1993), V.32, №13, p.2213.

Чувствительный элемент волоконно-оптического интерферометрического датчика электрического тока и магнитного поля, выполненный в виде уложенного по окружности отрезка кварцевого волоконного световода с внутренним линейным двойным лучепреломлением, и имеющим структуру с периодически повторяющимися вдоль оптического волокна оптическими параметрами, отличающийся тем, что указанная периодическая структура выполнена в виде спиральной структуры внутреннего линейного двойного лучепреломления, при этом шаг L_tw спирали, длина биений L_b внутреннего линейного двойного лучепреломления, температурный коэффициент α_b внутреннего линейного двойного лучепреломления, радиус R окружности уложенного отрезка волоконного световода, радиус r поперечного сечения волоконного световода, рабочая длина волны λ интерферометрического датчика и показатель преломления n_о(λ) световедущей оболочки волоконного световода выбраны из соотношения: где М=373,42°С;N=637,9°С.