Способ определения концентраций газовых компонентов слоя атмосферы на границе с гидросферой

Способ определения концентраций газовых компонентов слоя атмосферы на границе с гидросферой

Иллюстрации

Показать все

Реферат

Изобретение относится к определению газовых компонентов слоя атмосферы путем измерения гидрометеорологических параметров на границе атмосфера - гидросфера и может быть использовано при исследовании процессов взаимодействия атмосфера - океан, а также в обеспечении геоэкологического мониторинга морских объектов хозяйственной деятельности, включая мониторинг морских нефтегазоносных акваторий.

Известны способы определения концентраций газовых компонентов атмосферы [авторское свидетельство СССР №325579, кл. G01W 1/11, 1971; Briston M.UVDJAL for Simultaneous measurement of Tropospheris O₃ and SO₂. Optimization of the transmitter section. International laser Radar Conference Abgtracto, of papers, Part II p.p.347-350, 1990].

По способу [авторское свидетельство СССР №325579, кл. G01W 1/11, 1971] зондирование газового компонента атмосферы производится путем посылки в атмосферу импульсов света на двух разных длинах волн, находящихся в полосе поглощения зондируемого компонента, и приема рассеянного излучения, по мощности которого судят о концентрации компонента.

Недостаток способа состоит в низкой точности определения концентрации за счет неучета взаимного влияния всей совокупности газовых компонентов и допущения определяющего влияния одного из них.

По способу [Briston M.UVDJAL for Simultaneous measurement of Tropospheris O₃ and SO₂. Optimization of the transmitter section. International laser Radar Conference Abgtracto, of papers. Part II p.p.347-350, 1990] концентрации газовых компонентов определяют путем посылки по пересекающей слой трассе зондирования оптических импульсов на различных длинах волн, причем длины волн оптических импульсов выбирают в полосах поглощения определяемых газовых компонентов, и регистрации сигналов обратного рассеяния, по интенсивностям которых судят о значениях концентраций газовых компонентов.

Недостаток способа состоит в низкой точности определения концентраций газовых компонентов из-за наличия ошибки, обусловленной спектральной зависимостью показателя обратного рассеяния.

Повышение точности определения концентраций газовых компонентов за счет уменьшения влияния указанной ошибки частично решено в известном способе определения концентраций газовых компонент атмосферы [патент RU №2017139 С1 от 30.07.1994].

Для достижения поставленной цели в известном способе определения концентраций газовых компонентов слоя атмосферы [патент RU №2017139 С1 от 30.07.1994], заключающемся в том, что по основной трассе зондирования посылают оптические импульсы на различных длинах волн, причем длины волн оптических импульсов выбирают в полосах поглощения определяемых газовых компонентов и регистрируют сигналы обратного рассеяния, по интенсивностям которых судят о значениях концентраций газовых компонентов, оптические импульсы посылают не менее, чем по двум дополнительным трассам зондирования, причем направления дополнительных трасс выбирают таким образом, чтобы точки пересечения основной и каждой из дополнительных трасс лежали на обеих границах зондируемого слоя атмосферы.

При реализации известного способа световые импульсы посылают в атмосферу посредством лидара из точек, расположенных на прямой. Дополнительно к зондированию по основному направлению посылают импульсы из еще двух точек вдоль двух лучей, пересекающихся внутри слоя в некоторой точке и пересекающих основную трассу зондирования в точках пересечения ее с границами. Скорректированные на геометрический фактор (умноженные на квадрат расстояния зондирования) сигналы обратного рассеяния P_ki на длинах волн λ_ki, находящихся в полосе поглощения газового компонента, принимают из дополнительных точек и в точке их пересечения находят их отношение и вычисляют их величины.

По найденным отношениям, связанным с искомыми концентрациями, N_к, средними по слою, оптико-локационным уравнением определяют концентрацию каждого газового компонента.

При использовании известного способа погрешность концентрации N_к уменьшается при увеличении протяженности лучей зондируемого участка и достигает минимума при максимальной дальности зондирования. При этом повышение точности измерения газовых компонентов достигается за счет неизвестного исключаемого показателя обратного рассеяния. И если в условиях суши использование известного способа позволяет повысить точность измерения газовых компонентов, то в морских условиях реализация известного способа будет сопряжена с необходимостью исключения влияния внешних природных факторов.

Известно, что состав атмосферного аэрозоля над морской поверхностью складывается из солей морского происхождения, континентальной пыли и солей антропогенного происхождения. Попадание морских солей в воздух происходит в результате разбрызгивания и испарения морской воды с поверхности океана. Структура поверхности раздела океан - атмосфера значительно осложняется в результате постоянного присутствия пузырьков воздуха в воде и капель воды в воздухе. Пузыри и капли увеличивают поверхность взаимодействия двух сред и влияют на скорость и характер этого взаимодействия, что будет вносить существенную погрешность в определяемые параметры. При этом экстремальные значения гидрометеорологических характеристик имеют степенной закон распределения, что приводит к большим оценкам влияния, чем при обычно используемом экспоненциальном распределении экстремумов.

Кроме того, для достоверного получения конечных результатов измерений по пространственно-временным массивам наблюдений необходимо минимизировать погрешность оценки среднего арифметического значения измеряемого параметра. Экстремальные значения гидрометеорологических характеристик имеют степенной закон распределения, что приводит к большим оценкам влияния, чем при обычно используемом экспоненциальном распределении экстремумов.

Задачей предлагаемого технического решения является расширение функциональных возможностей способа с одновременным повышением достоверности определения концентраций газовых компонентов слоя атмосферы преимущественно на границе с гидросферой.

Поставленная задача решается за счет того, что в способе определения концентраций газовых компонентов слоя атмосферы, заключающемся в том, что по основной трассе зондирования посылают импульсы оптического излучения на различных длинах волн, причем длины волн импульсов оптического излучения выбирают в полосах поглощения определяемых газовых компонентов, регистрируют сигналы их обратного расстояния, по интенсивностям которых судят о значениях концентраций газовых компонентов, при этом импульсы оптического излучения посылают не менее чем по двум дополнительным трассам зондирования, причем направления дополнительных трасс выбирают так, чтобы точки пересечения основной и каждой из дополнительных трасс лежали на обеих границах зондирования, дополнительно в пограничном слое атмосферы над морской поверхностью методом протонного спинового эха выявляют механизм переноса и изменчивости потоков солей при различных гидрометеорологических условиях путем измерения скорости спин-решеточной релаксации в атмосферной влаге над морской поверхностью, причем измерение скорости спин-решеточной релаксации в морской воде выполняют путем применения многоимпульсной последовательности, состоящей из одного нутационного 180-градусного импульса и серии троек зондирующих импульсов (90° - τ₁-180°-τ₁ - 90°), позволяющей получить огибающую сигналов свободной индукции «за одно прохождение», при этом в качестве наблюдаемого сигнала в этой последовательности используется амплитуда сигнала свободной индукции следующего после первого 90-градусного импульса в тройке, при обработке измерений рассчитывают средние арифметические значения для каждой гидрометеорологической и оптической характеристики по дискретным наблюдениям в некотором пространственно-временном объеме, при минимизации погрешности учитывают распределение координат измерений путем ввода в вычисления локальных декартовых координат для рассматриваемой пространственно-временной области, при этом выполняют оценку закона распределения экстремальных значений гидрометеорологических характеристик путем статистики Герста.

Новые отличительные признаки, заключающиеся в том, что в пограничном слое атмосферы над морской поверхностью методом протонного спинового эха выявляют механизм переноса и изменчивости потоков солей при различных гидрометеорологических условиях путем измерения скорости спин-решеточной релаксации в атмосферной влаге над морской поверхностью, причем измерение скорости спин-решеточной релаксации в морской воде выполняют путем применения многоимпульсной последовательности, состоящей из одного нутационного 180-градусного импульса и серии троек зондирующих импульсов (90^о-τ₁ - 180°-τ₁ - 90°), позволяющей получить огибающую сигналов свободной индукции «за одно прохождение», при этом в качестве наблюдаемого сигнала в этой последовательности используется амплитуда сигнала свободной индукции следующего после первого 90-градусного импульса в тройке, при обработке измерений рассчитывают средние арифметические значения для каждой гидрометеорологической и оптической характеристики по дискретным наблюдениям в некотором пространственно-временном объеме, при минимизации погрешности учитывают распределение координат измерений путем ввода в вычисления локальных декартовых координат для рассматриваемой пространственно-временной области, при этом выполняют оценку закона распределения экстремальных значений гидрометеорологических характеристик путем статистики Герста, позволяют использовать метод протонного спинового эха для изучения процессов обмена веществом в пограничном слое атмосферы над морской поверхностью, который дает дополнительную информацию о механизме переноса и изменчивости потоков солей при различных условиях, а также минимизировать погрешность измерений.

Сущность предлагаемого технического решения поясняется чертежами.

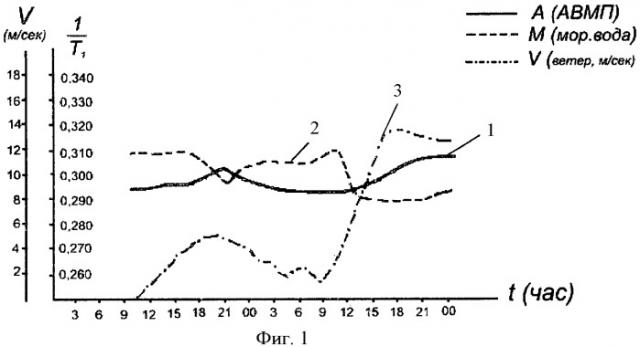
Фиг.1 - Изменение скорости спин-решеточной релаксации в АВМП в поверхностном слое морской воды при различных значениях скорости ветра. 1 - скорость спин-решеточной релаксации, 2 - поверхностный слой воды, 3 - скорость ветра.

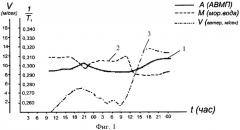
Фиг.2 - Пример кубической сетки.

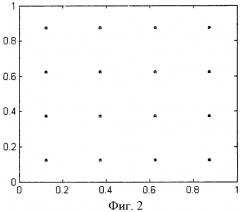
Фиг.3 - Отклонения D для LP_τ-последовательности в двойном логарифмическом масштабе. Кривая 4 - для одномерной, 5 - для двумерной, 6 - для трехмерной, 7 - для четырехмерной LP_τ-последовательности.

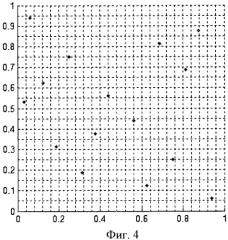
Фиг.4 - Расположение первых 16 точек LP_τ - последовательности на двумерной единичной области.

Исследование процессов обмена веществом между океаном и атмосферой представляет большой научный и практический интерес. Это объясняется прямым влиянием поступающих из океана солей на формирование и химический состав атмосферного аэрозоля, который как климатообразующий фактор характеризуется существенной нестационарностью пространственно-временного распределения и изменчивостью физико-химических свойств. Физические процессы, развивающиеся в пограничном слое атмосферы над морской поверхностью, оказывают определяющее влияние на образование и структуру аэрозольных слоев. От особенностей распределения и структуры атмосферного аэрозоля зависят такие важные процессы, как изменчивость радиационного баланса атмосферы, явления конденсации и сублимации в облачных системах, изменение оптических характеристик атмосферы, условия и характер распространения радиоволн УКВ диапазона [Кондратьев К.Я., Прокофьев М.А. Атмосферный аэрозоль и его воздействие на климат. Ж. ФАО, 1984, т.20, №11, с.1055-1063].

Полной гидродинамической теории сопредельных слоев океана и атмосферы в настоящее время не существует, как не существует единых представлений об особенностях функционирования трансформации и изменчивости потоков вещества, сопровождающих его перенос в специфических физических и физико-химических условиях пограничной структурной зоны раздела океан - атмосфера. Тем не менее результаты исследований последних лет (прежде всего экспериментальных) позволяют рассматривать многие из проблем взаимодействия на границе вода - воздух с достаточной степенью детализации, которая необходима для решения ряда прикладных задач. Применение метода протонного спинового эха для изучения процессов обмена веществом в пограничном слое атмосферы над морской поверхностью дает интересную информацию о механизме переноса и изменчивости потоков солей при различных условиях [Алекин О.А., Ляхин Ю.И. Химия океана. - Л.: Гидрометеоиздат, 1984, 338 с.].

Состав атмосферного аэрозоля над морской поверхностью складывается из солей морского происхождения, континентальной пыли и солей антропогенного происхождения. Попадание морских солей в воздух происходит в результате разбрызгивания и испарения морской воды с поверхности океана. Структура поверхности раздела океан - атмосфера значительно осложняется в результате постоянного присутствия пузырьков воздуха в воде и капель воды в воздухе. Пузыри и капли увеличивают поверхность взаимодействия двух сред и влияют на скорость и характер этого взаимодействия.

Вместе с каплями и брызгами с морской поверхности переходит в воздух довольно большое количество солей. Скорость выделения солей из океана в атмосферу, естественно, зависит от скорости ветра и описывается линейной зависимостью

где S - концентрация в воздухе над морем, мкг/м²;

V - скорость ветра, м/с;

а и b - коэффициенты.

Экспериментально определенные значения коэффициента а колеблются в пределах 0,05-0,07, а b - 0,42-0,61 [Береснев С.А., Грязин В.И. Физика атмосферных аэрозолей. - Е: Изд-во Уральского университета, 2008, 227 с.].

По данному уравнению (1) можно примерно оценить концентрацию солей в воздухе. Время жизни морских аэрозолей составляет приблизительно 1-2 суток.

Перенос и метаморфизация солей морской воды в атмосферу происходит не только при штормовых процессах (пенообразование, разбрызгивание), но и при испарении со спокойной (штилевой) морской поверхности, то есть только за счет одного физического испарения. При этом соли поступают в атмосферу в молекулярно-дисперсном состоянии. Основным фактором, обуславливающим перенос электролитов, является различие степени гидротации ионов, т.е. при испарении ионы выкосятся вместе с гидратной оболочкой [Петренчук О.П. Экспериментальные исследования атмосферного аэрозоля. - Л.: Гидрометеоиздат, 1979, 264 с. Бруевич С.В., Корж В.Д. Солевой обмен между океаном и атмосферой. - Океанология, 1971, 11, вып.5. с.11-15].

Интенсивность физического испарения солей с морской поверхности, судя по экспериментальным данным, не может превышать 0,1÷0,5 мг/л солей в конденсате. Определяющая роль в выведении морских солей в атмосферу принадлежит процессам разбрызгивания.

Многочисленные исследования химического состава атмосферы над морской поверхностью показали, что соотношение элементов в атмосферных осадках и аэрозолях отличаются и иногда значительно от соотношения этих же элементов в морской воде. Считается, что отличие полностью обусловлено фракционированием элементов при выделении с поверхности моря в атмосферу. На самом деле этому могут быть следующие причины:

а) фракционирование ионов непосредственно при переходе с морской поверхности в атмосферу;

б) преобразование состава аэрозолей в воздухе в результате взаимодействия с различными газами, испарения поверхности образовавшихся частиц и адсорбции на них различных примесей;

в) смешивание в воздухе солей морского происхождения с частицами, образованными на континенте за счет выветривания и производственной деятельности. Фракционирование элементов в процессе обмена между океаном и атмосферой определяется по отношению к натрию, как наиболее консервативному:

где х - любой химический элемент;

F - фактор фракционирования. Соотношение между элементами, конечно, могут значительно изменяться в зависимости от физико-географических условий.

Степень фракционирования при физическом испарении, судя по экспериментальным данным [Береснев С.А., Грязин В.И. Физика атмосферных аэрозолей. - Е: Изд-во Урал. ун-та, 2008, 227 с. Алекин О.А., Ляхин Ю.И. Химия океана. - Л.: Гидрометеоиздат, 1984, 338 с.], не превышает степени фракционирования при разбрызгивании. Это верно, поскольку оба вида фракционирования определяются соотношением между ионами на поверхности воды.

В настоящее время недостаточно исследованы физико-химические свойства морского аэрозоля и динамика переноса солей в пограничный слой атмосферы, а также мало изучены процессы обмена веществом на границе раздела океан - атмосфера в зависимости от физико-географических условий и в различные времена года и суток.

Результаты, полученные методом протонного спинового эха, по измерению скорости спин-решеточной релаксации 1/Т₁ в атмосферной влаге над морской поверхностью (АВМП) и поверхностном слое морской воды дают дополнительную информацию, наряду с оптическими и гидрохимическими методами, о динамике обмена и переносе солей в пограничном слое атмосферы раздела вода-воздух при различных условиях. Основные элементы теории ядерного магнитного резонанса (ЯМР) и физическая сущность ядерной магнитной релаксации в жидкости, а также блок-схема экспедиционного варианта спектрометра протонного спинового эха, разработанного для изучения данных процессов, рассмотрены в работах [Вашман А.А., Пронин И.С. Ядерная магнитная релаксация и ее применение в химической физике. - М.: Наука, 1979, 235 с. Зверев С.Б., Копвиллем У.Х. Применение многократных квантовых резонансов для изучения структуры жидкости. Ж ОАО, 1993, т.6, №7, с.778-782].

Для повышения точности и сокращения времени определения 1/Т₁ в АВМП и морской воде применена методика измерения с использованием многоимпульсной последовательности, состоящей из одного нутационного 180-градусного импульса и серии троек зондирующих импульсов (90°-τ₁ - 180°-τ₁ - 90°), позволяющей получить огибающую сигналов свободной индукции «за одно прохождение». В качестве наблюдаемого сигнала в этой последовательности используется амплитуда сигнала свободной индукции, следующего после первого 90-градусного импульса в тройке.

При настройке непрерывно следующих друг за другом троек импульсов интервалы τ₁ в тройках между импульсами и τ₂ между тройками импульсов выбраны такими, чтобы соблюдалось условие t_p<<τ₁<<τ₂, где t_p - длительность радиочастотного импульса. При этом τ₂ установлено достаточно коротким, чтобы исключить влияние самодиффузии молекул жидкости и в тоже время получить полную огибающую до А_∞≥А₀.

Помимо значительной экономии времени при измерении 1/Т₁ за одно прохождение не требуется длительной стабильности резонансных условий и температуры. Однако в многоимпульсной последовательности необходима весьма точная установка и высокая стабильность длительности зондирующих импульсов, т.к. ошибки из-за неправильной настройки их длительностей накапливаются, что ведет к искажению огибающей сигналов и неверному определению 1/Т₁.

Для устранения накопления ошибки при измерении 1/Т₁ за одно прохождение в последовательности троек применены фазовые сдвиги частот заполнения зондирующих 90- и 180-градусных импульсов.

Повторение троек импульсов n раз позволяет получить n точек зависимости

Величину 1/Т₁ при таком методе измерений [Вашман А.А., Пронин И.С. Ядерная магнитная релаксация и ее применение в химической физике. - М.: Наука, 1979, 235 с.] находят либо с помощью аппроксимации экспоненциальной кривой, либо с помощью соотношения

T₁=τ₀/ℓn2

Отбор проб АВМП проводился на высоте 10 м от морской поверхности с помощью специальной ловушки атмосферной влаги, выполненной на основе полупроводникового холодильника, при прокачке через нее атмосферного воздуха со строго определенной скоростью и за одинаковые промежутки времени. Пробы морской воды с поверхностного слоя отбирались с помощью батометра БМ-48. Работы по изучению динамики параметра 1/T₁ в АВМП и подстилающей морской поверхности проведены в прибрежной зоне Черного моря (ноябрь) на базе Экспериментального отделения МГИ ПАНУ в Кацивели. Район Черного моря интересен тем, что здесь в большей степени сказывается влияние на физико-химические свойства морского аэрозоля, примесей континентального и антропогенного происхождения, чем в открытых морях. Это позволяет более глубоко исследовать механизмы формирования и трансформации морского аэрозоля в прибрежных и океанических зонах.

Работы проводились со специальной платформы, оборудованной для проведения различных океанологических исследований, стоящей в 800 м от берега. Такая постановка эксперимента позволила проследить суточный ход изменения скорости спин-решеточной релаксации в АВМП в одной точке. На фиг.1 показано изменение параметра 1/T₁ в АВМП и поверхностном слое морской воды при различных значениях скоростей ветра.

По результатам натурных экспериментов при рассмотрении характера распределения величины 1/T₁ с учетом метеорологической обстановки можно сделать следующие выводы:

1. Величина скорости спин-решеточной релаксации 1/T₁ зависит от скорости ветра. Такая зависимость замечена и по ранее выполненным измерениям этого параметра 1/T₁ в Тихом океане. Общее увеличение значений 1/T₁ происходило при возрастании силы ветра более трех баллов. Изменение 1/T₁ в поверхностном слое воды обусловлено сложным гидрологическим режимом данного района и влиянием примесей антропогенного происхождения. В отдельных случаях скорость спин-решеточной релаксации в АВМП выше, чем в поверхностном слое морской воды. Это, по-видимому, связано с увеличением скорости фракционирования солей с поверхности моря в атмосферу, которая зависит от метеорологических условий и времени суток.

2. Средние значения параметра 1/T₁ в АВМП в прибрежной зоне Черного моря выше, чем в открытых частях Тихого океана. Здесь сказывается более сильное влияние примесей континентального и антропогенного происхождения.

3. Интересно также отменить, что по изменению скорости спин-решеточной релаксации в атмосферной влаге над морской поверхностью можно наблюдать соотношение между различными механизмами испарения при различных условиях.

Концентрация соли в атмосферной влаге оценивалась по формуле [Мельниченко Н.А. Процессы переноса и релаксации в водных растворах сильных электролитов. - В.: Дальнаука, 2005, 209 с.].

где E₀ - энергия активизации молекулярных движений;

R - универсальная газовая постоянная;

Т - температура измерения; Т_0÷150°K

С₀ и Сά - постоянные коэффициенты, характеризующие среднее время, в течение которого молекула существенно изменяет свое положение в пространстве при повороте или трансляции. Наибольшая концентрация соли в атмосферной влаге для данного района Черного моря составляет 10.03 мг/л, наименьшая 7.85 мг/л.

Результаты исследования атмосферной влаги в пограничном слое раздела морская поверхность - атмосфера методом протонного спинового эха показывают, что данный метод позволяет существенно дополнить информацию о влиянии процессов фракционирования, обмена, трансформации и переноса морских солей на формирование и физико-химические свойства морского аэрозоля при различных условиях.

В качестве метода оценки среднего арифметического значения гидрометеорологической характеристики по пространственно-временным массивам наблюдений применен метод, позволяющий минимизировать погрешность оценки среднего арифметического значения гидрометеорологической характеристики по пространственно временным массивам наблюдений.

В практике обработки гидрометеорологических наблюдений существует задача оценки среднего значения гидрометеорологической характеристики в некотором пространственно-временном объеме по дискретным наблюдениям. Каждое дискретное наблюдение фиксируется четырьмя координатами: временем, широтой, долготой и глубиной (высотой). Другими словами, значение гидрометеорологической характеристики в общем случае является функцией, заданной в четырехмерном координатном пространстве. В частных случаях эта размерность может принимать и меньшие значения. Размерность определяется числом координат точек наблюдений, значения которых меняются в массиве наблюдений. Например, для типичных задач по расчету среднего значения гидрометеорологической характеристики по дискретным наблюдениям:

1) по дискретным во времени измерениям в географической точке с фиксированными координатами на фиксированной глубине (высоте);

2) по одновременным наблюдениям в некоторой пространственной области на фиксированной глубине (высоте);

3) по наблюдениям в некотором районе в разные моменты времени и в разных точках на фиксированной глубине (высоте);

4) по наблюдениям в некотором фиксированном районе за некоторый интервал времени в некотором интервале глубин (высот).

Нумерация задач соответствует размерности пространства задания гидрометеорологической характеристики.

В настоящее время среднее арифметическое для любой задачи рассчитывают путем прямого суммирования всех измеренных значений, попадающих в рассматриваемый пространственно-временной объем, и делят на общее число измерений.

В действительности такой метод расчета среднего арифметического гидрометеорологической характеристики не позволяет получить минимально возможную погрешность в оценке среднего. Причиной этого является то, что в принятом методе игнорируется распределение точек наблюдения по пространственно-временному объему. Более того, точность оценки среднего значения применяемого метода уменьшается с увеличением размерности пространства координат наблюдений.

В заявляемом способе применен адекватный метод расчета среднего арифметического значения гидрометеорологической характеристики, минимизирующий погрешность, который заключается в следующем.

В общем случае задача определения среднего значения гидрометеорологической характеристики по значениям характеристики в дискретных пространственно-временных точках с математической точки зрения является задачей оценки среднего арифметического значения непрерывной функции в пространственно-временном объеме по ее значениям в дискретных точках. Погрешность в оценке среднего арифметического, при условии изотропности изменчивости функции, определяется структурой «неравномерности» расположения точек измерения в пространственно-временном объеме. Наименьшую погрешность дают точки, равномерно распределенные по рассматриваемому объему. Точки называются равномерно распределенными в n-мерном единичном кубе, если в любом гиперкубе число точек пропорционально объему гиперкуба [Соболь И.М. Многомерные квадратурные формулы и функции Хаара. - М., Наука, 1969. - 288 с.].

Формально это определяется следующим образом. Обозначим через Kⁿ единичный куб в n-мерном пространстве: Kⁿ состоит из всех точек Р с декартовыми координатами Р=(х₁,…,x_n), которые удовлетворяют неравенствам 0≤x_j≤1 (j=1, 2, …, n). Рассмотрим последовательность точек Р₀, P₁, …, P_i, …, принадлежащих кубу Kⁿ размерности n, и обозначим через S_N(G) количество точек Р с номерами 0≤i≤N-1, принадлежащими множеству G. Последовательность точек Р₀, P₁, …, P_i, … называется равномерно распределенной в Kⁿ (сокращенно p.p.), если для любого n-го параллелепипеда π с ребрами, параллельными координатным осям,

где V_π - объем параллелепипеда π. Можно доказать, что если G произвольная область, расположенная в Kⁿ и имеющая объем V_G, то из (5) вытекает, что

.

Таким образом, при больших N количество точек p.p. последовательности, принадлежащих любой области G, пропорционально объему G.

По теореме Вейля (Соболь И.М. Многомерные квадратурные формулы и функции Хаара. - М., Наука, 1969. - 288 с.) для того, чтобы {P_j} была p.p., необходимо и достаточно, чтобы для любой интегрируемой, по Риману, функции f(P) выполнялось соотношение

Выражение (2) является оценкой среднего арифметического. Оценка погрешности (6) определяется выражением

где С - константа, разная для функций с различной изменчивостью, D - отклонение распределения точек от p.p.

Отклонение D определяется следующим образом. Рассмотрим в Kⁿ сетку, состоящую из N произвольных точек Р₀, Р₁, …,P_N-1. Каждой точке Р из Kⁿ поставим в соответствие параллелепипед π_P с диагональю ОР (O - начало координат). Объем V_P этого параллелепипеда равен произведению x₁…x_n координат точки Р. Отклонением сетки Р₀,Р₁,…,P_N-1 называется число

где верхняя грань берется по всем Р∈Kⁿ.

Для того чтобы последовательность точек была p.p., необходимо и достаточно, чтобы при N→∞

Характеристика D(P₀,…,P_N-1) является весьма сложной функцией от структуры расположения точек. Верхняя граница D≤N, нижняя граница ее до сих пор не известна (за исключением случая n=1, когда inf D=1/2). Существует предположение, что наилучшая возможная оценка D для n-мерной сетки, состоящей из N точек, равна

Необходимо отметить, что в гидрометеорологии исследователи ошибочно полагают, что кубические сетки (их называют «регулярные», «равномерные» и т.п.) всегда очень «хорошие», и целью сбора информации является получение измерений на такой сетке. Кубическая сетка для N=М² точек задается координатами

где i₁, i₂, …, i_n - независимо пробегают значения 1, 2, …, М. На фиг.2 изображена кубическая сетка при n=2, М=4.

Нетрудно проверить, что для таких сеток значение будет максимальным, например, в точке P'=(1/2M,1,1,…,1), когда S_N(π_p')=o, NV_P'=N/2M=M^n-1/2. Следовательно,

Из формулы (8) следует, что при n=1 кубические сетки оптимальны. Однако с увеличением n равномерность сеток (7) ухудшается, и порядки в формуле (8) приближаются к наихудшим, равным N. Уже при n=2 порядок (8) оказывается равным - такой же порядок соответствует случайным сеткам, состоящим из N независимых случайных точек, равномерно распределенных в Kⁿ. Значит, при n≥3 сетки (11) асимптотически хуже случайных.

Пусть в Kⁿ задано множество точек наблюдений за гидрометеорологической характеристикой Р₀, Р₁, …, P_N-1. Этот набор точек далек от p.p. Необходимо определить такое подмножество точек {Р'}_N0∈{Р}_N, которое образует сетку с наибольшей степенью равномерного распределения. Решение этой задачи будем искать следующим образом. Определим подходящую опорную сеть точек, имеющую p.p. Сравнивая координаты точек наблюдений с координатами точек опорной p.p. сетки, найдем искомое подмножество {Р'}_N0∈{Р}_N, которое будет давать минимальную ошибку в оценке среднего арифметического, в соответствии с (7).

В вычислительной математике построено много вариантов сеток, близких к p.p. Для нашей задачи целесообразно выбрать такую сетку с последовательностью точек Q₀, Q₁, …, Q_i, …, которая удовлетворяет трем требованиям:

- равномерность распределения сетки должна быть асимптотически оптимальной;

- равномерность расположения точек должна наблюдаться не только при N→∞, но уже при малых N;

- алгоритм расчета точек Q_i должен быть достаточно простым.

Этим требованиям удовлетворяют, например, так называемые LP_τ-последовательности (Соболь И.М. Многомерные квадратурные формулы и функции Хаара. - М., Наука, 1969. - 288 с.).

Не излагая теоретического обоснования p.p. свойств этих последовательностей, приведем простой алгоритм расчета.

В этом алгоритме координаты (q_i1,…,q_in) точки Q_i из LP_τ-последовательности вычисляется по формуле

где i=e_m…e₂e₁ - представление i в двоичной системе, - двоично-рациональные числа вида , числители которых табулированы.

В таблице 1 представлены для 1≤s≤20 и 1≤j≤4, что позволяет легко вычислять точки Q_i размерности n≤4 в количестве N≤2²⁰.

Отклонения D для LP_τ-последовательности представлены на фиг.3.

Таблица 1
Таблица значений
s	n
1	2	3	4
1	1	1	1	1
2	1	3	1	3
3	1	5	7	1
4	1	15	11	5
5	1	17	13	31
6	1	51	61	29
7	1	85	67	81
8	1	255	79	147
9	1	257	465	433
10	1	771	721	149
11	1	1285	823	719
12	1	3855	4091	3693
13	1	4369	4125	3841
14	1	13107	4141	11523
15	1	21845	28723	16641
16	1	65535	45311	49925
17	1	65537	53505	16671
18	1	196611	250113	83229
19	1	327685	276231	515921
20	1	983055	326411	482707

Для примера на фиг.3 представлено для двумерной единичной области положение LP_τ-последовательности для первых 16 точек. Положение точек свидетельствует, что оно значительно отличается от «регулярного расположения», представленного на фиг.2.

Алгоритм выбора репрезентативных точек можно представить в следующем виде: Задано: множество из N точек наблюдений Р₀,Р₁,…,P_N-1 в n-мерном кубе Kⁿ, n=1, 2, 3, 4. Каждая точка наблюдений представлена нормированными координатами Р=(х₁,…,x_n), 0≤x_j≤1, j=1, 2, …, n.

Требуется: определить подмножество точек {Р'}_N0∈{Р}_N, которые дают наименьшую ошибку в оценке среднего арифметического функции, измеренной в этих точках (т.е наиболее репрезентативный набор точек измерений для оценки среднего или, что тождественно, образуют сетку с наибольшей степенью равномерного распределения).

Инициация: T_k=Т₀=⌀ - набор точек-кандидатов на k шаге.

Последовательность операций решения:

1. Вычислить N точек Q_k(k=1,…N) LP_τ-последовательности по формуле (13).

2. Последовательно для каждого k от 1 до N:

2.1. Для каждой точки Q_k найти ближайшую в евклидовой метрике точку среди множества точек {P₁,…,P_N}\T_k-1, , и добавить ее в набор точек-кандидатов на k, образуя .

Вычислить отклонение D_k=D(T_k) для точки P_i по формуле (8).

3. Последовательно для каждого k от 1 до N найти D_0k=max(D₁,…,D_k).

4. Найти k₀, для которого существует минимальное значение D_0k.

Результат: набор точек является искомым множеством точек наблюдений, дающим минимальную ошибку в оценке среднего арифметического.

Таким образом, показано, что при расчете среднего арифметического значения гидрометеорологической характеристики по дискретным наблюдениям в некотором пространственно-временном объеме для миним