Устройство и способ комбинаторного кодирования сигналов с низкой сложностью

Устройство и способ комбинаторного кодирования сигналов с низкой сложностью

Иллюстрации

Показать все

Реферат

Область техники

Настоящее изобретение относится, в общем, к кодированию векторов и, в частности, к комбинаторному Факторному Импульсному Кодированию векторов с низкой сложностью.

Уровень техники

Способы кодирования векторных или матричных величин для речи, аудио, изображений, видео и других сигналов хорошо известны. Один такой способ, описанный в патенте США № 6236960 (автор Пенг и др.), который включен в данный документ посредством ссылки, известен как Факторное Импульсное Кодирование (или FPC). FPC может кодировать вектор x _i с использованием общего количества M битов, при условии, что

, (1)

и все величины вектора x _i вместе имеют такие целые значения, что -m ≤ x _i ≤ m, где m является полным количеством импульсов единичной амплитуды, а n является длиной вектора. Общее количество M битов используется, чтобы закодировать N комбинаций максимально эффективным способом так, чтобы следующее выражение, которое описывает теоретически минимальное количество комбинаций, оставалось истинным:

(2)

В этом неравенстве является количеством комбинаций d ненулевых элементов вектора в n положениях и задается как

, (3)

является количеством комбинаций d ненулевых элементов вектора при m полных единичных импульсах и задается как

, (4)

и представляет комбинации, требуемые для описания полярности (знака) d ненулевых элементов вектора. Выражение min(m,n) позволяет учесть случай, когда количество импульсов единичной магнитуды превышает длину n вектора. Способ и устройство кодирования и декодирования векторов такой формы полностью были описаны в предшествующем уровне техники. Более того, практическая реализация этого способа кодирования была описана в стандарте 3GPP2 C.S0014-B, где длина вектора n=54 и количество импульсов единичной магнитуды m=7 производят M=35-битное кодовое слово.

Несмотря на то, что эти значения n и m не причиняют никакой чрезмерной нагрузки сложности, более высокие значения могут быстро причинить проблемы, особенно в мобильных переносных устройствах, которым нужно сохранять память и вычислительную сложность как можно меньшими. Например, использование этого способа кодирования для некоторых применений (таких как кодирование аудио) могут требовать n=144, m=28, или выше. В таких обстоятельствах затраты, связанные с вычислением комбинаторного выражения с использованием способов из предшествующего уровня техники, могут быть слишком высоки для практической реализации.

Рассматривая эти затраты более подробно, мы можем переписать Ур.3 как

(5)

Непосредственная реализация проблематична, поскольку потребует 197 бит точности в числителе и 98 точности в делителе для получения 99-битного частного. Поскольку большинство цифровых сигнальных процессоров (DSP), используемых в сегодняшних переносных устройствах, обычно поддерживают только операции перемножения 16 бит × 16 бит, необходимо будет использовать специальные процедуры умножения/деления с многократной точностью. Такие процедуры требуют последовательности вложенных операций перемножения/накопления, которые обычно требуют порядка k операций перемножения/накопления (MAC), где k является количеством 16-битных сегментов в операнде. Так, исполнение одного 197×16-битного перемножения потребует минимум 13 операций MAC плюс операции сдвига и хранения. Выражение делителя вычисляется похожим способом для получения 98-битного результата. Дополнительно требуется 197/98-битное деление, которое является чрезвычайно сложной операцией, таким образом, вычисление всего отношения факториалов в Ур.5 потребует значительных ресурсов.

Для попытки снижения сложности Ур.5 можно переписать для распределения операций деления, чтобы получить следующее:

(6)

В этом выражении динамический диапазон операций деления уменьшен, но, к сожалению, нужна повышенная разрядность частного для точного представления деления на 3, 7, 9 и т.д. Чтобы разместить такую структуру, также требуется операция округления для гарантии целого результата. При большом количестве операций деления с высокой точностью такая реализация не решает адекватно проблему сложности для больших m и n, и более того, потенциально может произвести неправильный результат из-за накопленных погрешностей точности.

В еще одной реализации, Ур.5 может быть реорганизовано следующим образом:

(7)

Если это выражение оценивать слева направо, результат всегда производить целое значение. Несмотря на то, что этот способ контролирует вопрос точности и динамического диапазона в какой-то степени, большие значения m и n также требуют широкого использования операций перемножения и деления многократной точности.

Наконец, для того чтобы минимизировать вычислительную сложность, возможно предварительно вычислять и сохранять все комбинации факториалов в таблице поиска. Так, все значения могут быть просто сохранены в матрице n × m и подходящим образом извлечены из памяти с использованием нескольких тактов процессора. Проблема этого подхода, однако, состоит в том, что по мере того, как n и m становятся больше, также растут и требования связанной памяти. Используя предыдущий пример, потребует 144×28×=52,416 байт для хранения, что неприемлемо для большинства мобильных переносных устройств. Поэтому существует необходимость в способе и устройстве комбинаторного Факторного Импульсного Кодирования векторов с низкой сложностью.

Краткое описание чертежей

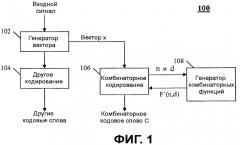
Фиг.1 - блок-схема кодера.

Фиг.2 иллюстрирует генерацию кодового слова.

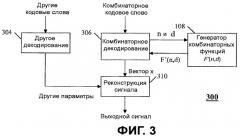
Фиг.3 - блок-схема декодера.

Фиг.4 - блок-схема последовательности операций, показывающая работу Генератора Комбинаторной Функции с Фиг.1 и Фиг.3.

Фиг.5 - блок-схема последовательности операций, показывающая работу кодера с Фиг.1.

Фиг.6 - блок-схема последовательности операций, показывающая работу декодера с Фиг.3.

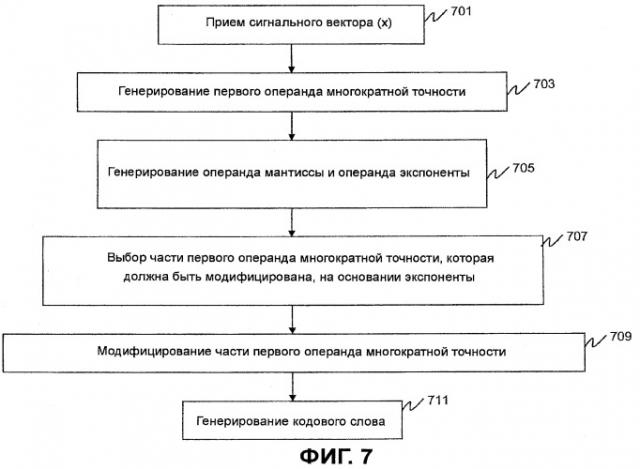
Фиг.7 - блок-схема последовательности операций, показывающая работу схемы комбинаторного кодирования с Фиг.1.

Фиг.8 - блок-схема последовательности операций, показывающая работу схемы комбинаторного декодирования с Фиг.3.

Подробное описание

Для того чтобы удовлетворить вышеупомянутую необходимость, в данном документе представлены способ и устройство комбинаторного Факторного Импульсного Кодирования векторов с низкой сложностью. Во время работы кодера принимается сигнальный вектор (x). Первый операнд () многократной точности будет сгенерирован на основании сигнального вектора, который должен быть закодирован. Генерируются операнд мантиссы и операнд экспоненты. Как операнд мантиссы, так и операнд экспоненты представляют второй операнд многократной точности, который основан на сигнальном векторе, который должен быть закодирован. Выбирается часть , которая должна быть модифицирована на основании операнда экспоненты. Часть модифицируется на основании операнда мантиссы для получения модифицированного операнда (). Наконец, генерируется кодовое слово многократной точности для использования в соответствующем декодере.

Настоящее изобретение охватывает способ работы кодера, который кодирует кодовое слово (C) из вектора (x). Способ содержит этапы приема вектора x который должен быть закодирован, генерирования первого операнда () многократной точности на основании x, и генерирования операнда (M) мантиссы и операнда (h) экспоненты. Операнд мантиссы и операнд экспоненты представляют второй операнд () многократной точности, который основывается на сигнальном векторе, который должен быть закодирован. Затем выбирается часть , которая должна быть модифицирована, на основании операнда экспоненты, и часть модифицируется на основании операнда мантиссы и указателя положения для получения модифицированного операнда (). Наконец, генерируется кодовое слово (C) на основании .

Настоящее изобретение дополнительно охватывает кодер, содержащий схему комбинаторного кодирования, выполняющую этапы приема вектора x, который должен быть закодирован, генерирования первого операнда () многократной точности на основании x и генерирования операнда (M) мантиссы и операнда (h) экспоненты. Операнд мантиссы и операнд экспоненты представляют второй операнд () многократной точности, который основан на сигнальном векторе, который должен быть закодирован. Затем выбирается часть , которая должна быть модифицирована, на основании операнда экспоненты, и часть модифицируется на основании операнда мантиссы и указателя положения для получения модифицированного операнда (). Наконец, генерируется кодовое слово (C) на основании .

Настоящее изобретение дополнительно охватывает способ работы декодера, который генерирует вектор (x) из кодового слова (C). Способ содержит этапы приема кодового слова (), генерирования первого операнда () многократной точности на основании и генерирования операнда (M) мантиссы и операнда (h) экспоненты. Операнд мантиссы и операнд экспоненты представляют второй операнд () многократной точности, который основан на кодовом слове. Выбирается часть , которая должна быть модифицирована, на основании операнда экспоненты, и часть модифицируется на основании операнда мантиссы и указателя положения для получения модифицированного операнда (). Положение (k-1)-ого ненулевого элемента вектора x декодируется, и вектор (x) генерируется на основании положения .

Настоящее изобретение дополнительно охватывает декодер, содержащий схему комбинаторного декодирования, выполняющую этапы приема кодового слова (), генерирования первого операнда () многократной точности на основании и генерирования операнда (M) мантиссы и операнда (h) экспоненты. Операнд мантиссы и операнд экспоненты представляют второй операнд () многократной точности, который основан на кодовом слове. Выбирается часть , которая должна быть модифицирована, на основании операнда экспоненты, и часть модифицируется на основании операнда мантиссы и указателя положения для получения модифицированного операнда (). Положение (k-1)-ого ненулевого элемента вектора x декодируется, и вектор (x) генерируется на основании положения .

Обращаясь теперь к чертежам, на которых подобные ссылочные позиции обозначают подобные компоненты, Фиг.1 является блок-схемой кодера 100. Кодер 100 содержит генератор 102 вектора, схему 106 комбинаторного кодирования, генератор 108 комбинаторных функций и другую схему 104 кодирования. Во время работы входной сигнал, который должен быть закодирован, принимается генератором 102 вектора. Как известно из уровня техники, входной сигнал может содержать речь, аудио, изображение, видео, и другие сигналы.

Генератор 102 вектора принимает входной сигнал и создает вектор x _i. Генератор 102 вектора может содержать любое количество парадигм кодирования, включая, но не в качестве ограничения, кодирование речи с помощью Линейного Предсказания с Мультикодовым Управлением (CELP), как описано Пенгом и др., кодирование областей преобразования для аудио, изображений и видео, включая способы, основанные на Дискретном Преобразовании Фурье (DFT), Дискретном Косинусном Преобразовании (DCT) и Модифицированном Дискретном Косинусном Преобразовании (MDCT), кодирование вейвлет-преобразований, прямую временную импульсно-кодовую модуляцию (PCM), дифференциальную PCM, адаптивную дифференциальную PCM (ADPCM) или любую из семейства методик кодирования поддиапазонов, которые хорошо известны в уровне техники. Фактически любой сигнальный вектор, имеющий форму, обозначенную выше, может быть эффективно обработан согласно настоящему изобретению.

Схема 106 комбинаторного кодирования принимает вектор x _i и использует Факторное Импульсное Кодирование для получения кодового слова C. Как обсуждалось выше, Факторное Импульсное Кодирование может кодировать вектор x _i с использованием общего количества M бит, при условии, что , и все величины вектора x _i вместе имеют такие значения, что -m ≤ x _i ≤ m, где m является полным количеством импульсов единичной амплитуды, а n является длиной вектора. Как обсуждалось выше, более высокие значения n и m могут быстро причинить проблемы, особенно в мобильных переносных устройствах, которым нужно сохранять память и вычислительную сложность как можно меньшими.

Чтобы решить этот вопрос, генератор 108 комбинаторных функций использует методику с низкой сложностью для получения . Схема 106 комбинаторного кодирования затем использует для получения кодового слова C. Схема 106 использует приближения (биты точности) с относительно низкой разрядностью комбинаций факториалов, которые обеспечивают достаточную точность только для того, чтобы сгенерировать правильное кодовое слово. То есть, пока сохраняются конкретные свойства, подходящее приближение функции является достаточным для гарантии того, что результирующее кодовое слово однозначно декодируемо. Чтобы описать генерацию функции , сначала выведем функцию которая является подходящим приближением Первым этапом возьмем логарифм с произвольным основанием a от Ур.5 и выполним обратное преобразование к логарифму по основанию a от реорганизованных членов

, (8)

где функция . Далее, определим функции и заменим в Ур.8 таким образом

(9)

где , , и .

Однако, согласно предпочтительному варианту настоящего изобретения, нет необходимости в том, чтобы и были эквивалентны для получения однозначно декодируемого кодового слова. Существует только два условия, которые с достаточностью должны выполняться

≥ (10)

и

≥ (11)

Для первого условия ограничение просто говорит о том, что, если <, тогда буду пересекаться кодовые пространства, и следовательно, будет более одного входа, способного генерировать конкретное кодовое слово, таким образом, кодовое слово не будет однозначно декодируемым. Второе условие утверждает, что для заданных n, d «погрешность» должна быть больше или равна, чем сумма членов погрешности, связанной с предыдущим элементом рекурсивной последовательности, описанной Пенгом и др. в патенте США № 6236960. Можно показать, что = истинно только, если комбинаторное выражение в точности является следующим: . Однако, несмотря на то, что неравенство Ур.11 является достаточным, нет необходимости в его истинности для всех n и d. Для таких величин может удовлетворять другому неравенству, выводимому из Ур.31 документа Пенга и др. и определяемому как

(12)

В этом случае Ур.11 должно выполняться в строгом смысле для конкретных (m,k),(m≤n),(k≤d), то есть

>, m≤n, k≤d (13)

Возвращаясь к Ур.9, нам требуется сгенерировать путем создания функций с приближениями низкой сложности для исходных функций так, чтобы

(14)

и где удовлетворяются условия Ур.10 и 11. Рассматривая , мы можем аппроксимировать эту функцию так, чтобы ≥, . Если мы выберем a=2 и затем ограничим 32-мя битами точности, получившиеся операции можно легко реализовать в переносных мобильных устройствах, поскольку большинство DSP поддерживает однотактовые 32-битные сложения. Поэтому зададим

, (15)

где l(i) - коэффициент сдвига, который может изменяться в зависимости от i. В предпочтительном варианте l(i)=l=21, но многие другие варианты значений также возможны. В этом примере коэффициент эквивалентен сдвигу на l бит влево, а функция отсекает дробные биты, округляя до следующего наибольшего целого, и, наконец, коэффициент сдвигает результат обратно вправо на l бит. Используя такую методику, функция ≥ для всех i≥1, а также обеспечивает достаточный динамический диапазон и точность с использованием только 32 бит, поскольку 9 бит положительной разрядности в области определения могут представлять 512-битное число. Для того чтобы избежать сложности с вычислением этих величин в реальном времени, их можно вычислить предварительно и хранить в таблице с использованием только 144 × 4 байт памяти для примера с . Используя похожую методику аппроксимации , получаем

(16)

где функция используется из-за вычитания величины из общего количества. Это гарантирует, что≤, так что вклад будет гарантировать ≥. Несмотря на то, что l(j) предполагает многие значения в зависимости от m и n, в предпочтительном варианте используется значение l(j)=l=14 для переменного коэффициента сдвига. Как и , может быть предварительно вычислена и сохранена в таблице с использованием только 28 × 4 байт памяти для примера с . Для определения нам необходимо сначала определить k как

(17)

При определенных выше и k предпочтительно является 32-битным числом с 8-битным беззнаковым целым компонентом и 24-битным дробным компонентом . Используя это, мы можем вывести ≥, полагая , и взяв обратное преобразование от логарифма по основанию 2, чтобы получить . Затем мы можем использовать разложение в ряд Тейлора для оценки дробного компонента с нужной точностью, представленной как , округляя результат с использованием функции округления до наименьшего ближайшего, и затем подходящим образом сдвигая результат для формирования результата с многократной точностью (имеющий только l значащих бит), так что

(18)

где - коэффициент целочисленного сдвига, применяемый к результату разложения в ряд Тейлора. Здесь l является коэффициентом сдвига, используемый аналогично как в Ур.15 и 16 для обеспечения ≥. Однако поскольку не может быть практически предварительно вычислена для эффективной работы в реальном времени, нужна высокая осторожность при задании точных операций, необходимых как в кодере, так и в декодере для гарантии того, что реконструированный сигнальный вектор в точности совпадает с входным сигнальным вектором. Стоит отметить, что может быть получена левым сдвигом , который может быть точно представлен посредством l бит.

В обсуждении выше функции , и были выбраны так, чтобы отдельная оценка гарантировала, что Однако необходимо только, чтобы общий результат удовлетворял этому условию. Например, и могут быть как описано выше, а может быть более близкой к функцией, которая может отбрасывать или округлять наименее значащие биты так, чтобы могла быть меньше для некоторых значений k. Это приемлемо, пока такой эффект мал относительно эффекта и , так что свойства Ур.10 и Ур.11 все еще оставались бы истинными.

Также любые функции , и могут быть использованы без потери общности, пока свойства Ур.10 и Ур.11 сохраняются. Осторожность должна быть проявлена, однако, в том, что может случиться увеличение битовой скорости, если используется слишком малая точность. Стоит также отметить, что существует характерное соотношение между битовой скоростью и сложностью, и для больших значений m и n увеличение в 1 или 2 бита может быть приемлемым компромиссом за значительное увеличение точности.

Далее будет описано формулирование частичного кодового слова C для положений и магнитуд в схеме 106 комбинаторного кодирования. Пусть - положения ненулевых импульсов (в возрастающем порядке), а - магнитуды в соответствующих положениях в векторе x. Код для положений импульсов задается как

, (19)

а код для магнитуд импульсов задается как:

(20)

Таким образом, формулирование этого кодового слова требует сложения чисел ν и многократной точности. Подобные операции вычитания нужны в декодере. Эти операции также добавляют сложности способу FPC, когда m и n велики. Рассмотрим кодирование/декодирование аудиосигнала в многоуровневой системе кодирования. Эта методика используется для кодирования преобразования остаточного сигнала погрешности на трех уровнях многоуровневой системы. Пусть размер 20мс блока равен n=280 и одинаков для всех уровней. Количество импульсов для кодирования зависит от битовой скорости каждого уровня. Если скорости уровней 8 Кбит/с, 16 Кбит/с или 32 Кбит/с, то им понадобится 160 бит, 320 бит и 640 бит для кодирования 20 мс блока, соответственно. С использованием способа FPC блок длины 280 может быть закодирован с помощью 28, 74, и 230 импульсов для 160 бит, 320 бит и 640 бит на уровень, соответственно. Операции с многократной точностью в уравнениях (19) и (20) выполняются на цифровом сигнальном процессоре, который обычно оперирует 16-битными словами. Таким образом, для формирования 160-битного кодового слова необходимо выполнить операции сложения с 10 словами, а для 640-битного кодового слова операции сложения должны быть выполнены для более чем 40 слов. Каждая операция сложения занимает 4 блока (генерирование переноса разряда, перемещение в массив, сложение с переносом разряда). Следовательно, кодирование/декодирование k-битного кодового слова на p уровнях многоуровневой системы требует операций/сек. Для разных значений n, m и p сложность операций сложения/вычитания с многократной точностью показана в Таблице 1. В этой таблице WMOPs обозначает взвешенное значение миллионов операций в секунду (Weighted Millions of Operation Per Second).

Таблица 1Сложность сложения/вычитания в кодировании/декодировании FPC с помощью известного из уровня техники способа
Количество уровней (p)	Размер блока (n)	Битовая скорость уровня/Бит на 20 мс блок (k)	Количество импульсов (m)	Сложность сложения/вычитания с многократной точностью
333	280280280	8 Кбит/с/16016 Кбит/с/32032 Кбит/с/640	2874230	0,64 WMOPs3,48 WMOPs22,0 WMOPs

Из Таблицы 1 видно, что, когда битовая скорость удваивается, сложность сложения с многократной точностью возрастает в шесть раз.

Как упоминалось выше, комбинаторная функция заменяется приближенной функцией , которая задается как

, (21)

где

(22)

и является приближением функции , задаваемая как:

(23)

где разбито на целый и дробный компоненты k, а - остаточный член малого порядка разложения в ряд Тейлора дробного компонента k. На основании вышеопределенных функций и сначала получается таким образом, что неравенство однозначной декодируемости

> (24)

удовлетворяется для всех n и d.

Возвращаясь к Ур. 19 и 20, замена приближенными функциями действительных функций F приводит к следующему:

, (25)

(26)

Двоичное представление , полученное из Ур. 23, имеет нулей окончания, если . была получена как число с многократной точностью путем сдвига влево ( сдвигов) -битного числа. Поскольку замыкающие h бит являются нулями, эти замыкающие h бит кодового слова не будут модифицированы, когда мы прибавим к существующей частичной сумме в Ур.25. Чтобы эффективно использовать это свойство, вычисляется в псевдоформате с плавающей запятой, т.е. функция выводит -битную мантиссу (M) и соответствующую неотрицательную экспоненту (h). -битная мантисса (M) определяется как

, (27)

а экспонента h определяется как

. (28)

Теперь суммирование в Ур.25 и 26 может легко использовать тот факт, что слова не модифицируются, когда прибавляется к частичной сумме.

Вышеприведенный способ на самом деле снижает в некоторой степени сложность. Однако перенос разряда, сгенерированный во время операции, возможно придется сохранять до конца кодового слова. Впоследствии мы покажем, что, если удовлетворяет конкретным условиям, то перенос разряда придется сохранять до намного меньшей части всего кодового слова.

Сначала раскроем, что перенос разряда сохранится на одно дополнительное кодовое слово, если будут складываться (как в Ур.19) в точности комбинаторные функции , и суммирование проводится в возрастающим порядком k

, (29)

т.е. частичная сумма , к которой прибавляется , задается как

. (30)

Можно показать, что операнд с многократной точностью меньше, чем . Максимальное отношение к меньше, чем . Это отношение является бесконечностью при , которое также является максимально возможным значением k. Поскольку , перенос разряда придется сохранить в этом конкретном случае. Для других значений k это отношение не больше, чем меньшее из n и m. Таким образом

+<, (31)

Поскольку меньше 32768, то вышеприведенное суммирование не приведет к сохранению переноса разряда более, чем на одно дополнительное кодовое слово. Это предполагает, что, если мы используем в точности комбинаторные функции в упорядоченном суммировании (29), то мы получим преимущество сохранения переноса разряда только на одно дополнительное кодовое слово, однако, в точности комбинаторные функции не имеют преимущества замыкающих нулей, и поэтому сложение выполняется по длине .

Ясно, что нам нужно создать приближенные функции так, чтобы в дополнение к однозначной декодируемости и замыкающим нулям упорядоченное сложение в Ур.29 не требовало сохранения переноса разряда. Можно показать, что частичная сумма (первое кодовое слово с многократной точностью), к которой прибавляется , задается как

, (32)

которая меньше, чем . Поэтому неравенство

<, (33)

является достаточным, чтобы при добавлении к для генерации (модифицированное кодовое слово с многократной точностью),

, (34)

перенос разряда сохранился только на одно дополнительное кодовое слово. Это было эмпирически определено для , заданной уравнениями 21, 22 и 23. Кроме неравенства однозначной декодируемости нам нужно, чтобы выполнялось неравенство частичных сумм, т.е.