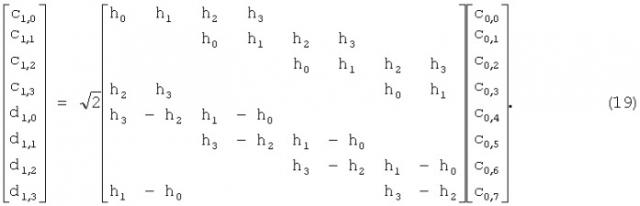Устройство обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области на основе дискретного вейвлет-преобразования

Устройство обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области на основе дискретного вейвлет-преобразования

Иллюстрации

Показать все

Реферат

Изобретение относится к области гидролокации и радиолокации, а именно - к обнаружителям сложных широкополосных частотно-модулированных сигналов известной формы на фоне аддитивной помехи.

Известно, что реализация оптимального приема при решении задачи обнаружения сигналов на фоне помех во многом определяется уровнем знаний о принимаемом сигнале.

Для сигналов с неизвестной начальной фазой оптимальным является квадратурный приемник [2-4] (аналог), обеспечивающий незначительные потери (1-1.2 дБ) по сравнению с согласованной фильтрацией. Основным недостатком квадратурного приема является ограниченность его применения только для класса узкополосных сигналов. В случае использования широкополосных сигналов необходима многоканальная схема, осуществляющая квадратурную фильтрацию по каждой составляющей.

Если фазовый спектр сигнала неизвестен, то используют энергетические методы и устройства приема [2-4] (аналог), представляющие собой последовательное выполнение операций фильтрации, квадратичного детектирования и интегрирования. Недостатком таких методов является «эффект подавления малого сигнала», что является следствием того факта, что выходное отношение сигнал/помеха (ОСП) пропорционально квадрату входного ОСП.

Если же форма принимаемого сигнала s(t) полностью известна (за исключением амплитуды A и времени прихода сигнала t₀: As(t-t₀)), то потенциальную помехоустойчивость при решении задачи обнаружения сигналов (в том числе и широкополосных частотно-модулированных) на фоне белого шума, в принципе, обеспечивает корреляционный приемник или согласованный фильтр [1 (с.339-343), 2-4] (аналог).

Причем помехоустойчивость этих обоих методов обнаружения известного сигнала (коррелятора и согласованного фильтра) в теоретическом смысле абсолютно одинакова. Обобщенное отношение сигнал/помеха (ОСП) на выходе данных обнаружителей, определяемое как отношение приращения постоянной составляющей выходного процесса - математического ожидания E[y(t)], обусловленное наличием полезного сигнала, к дисперсии выходного процесса в случае отсутствия сигнала D[y₀(t)], равно отношению удвоенной энергии сигнала E_s (с учетом случайной амплитуды) к спектральной плотности помехи N [1]

Данные методы обнаружения известного сигнала неявно предполагают один из видов одномерного представления сигнала и помехи: либо в спектральной области (согласованная фильтрация), либо во временной области (корреляционный прием).

Однако для входного процесса x(t) гидролокационного или радиолокационного приемника возможно также и двумерное представление - в масштабно-временной области, получаемое путем применения т.н. вейвлет-преобразования (ВП) [5-9].

Непрерывное ВП можно определить как скалярное произведение исследуемого процесса x(t) и базисных вейвлет-функций ψ_ατ(t) [5]

где черта сверху обозначает операцию комплексного сопряжения.

Общий принцип построения базиса ВП состоит в использовании масштабных преобразований с параметром сжатия α и смещений с параметром сдвига τ исходной вейвлет-функции ψ(t) (т.н. материнского вейвлета)

Чтобы быть вейвлетом, базисные функции ψ_ατ(t)∈L² (R) должны обладать рядом необходимых свойств [5-9]. Они должны быть: квадратично-интегрируемыми, знакопеременными (и обладать нулевым средним), вейвлеты должны стремиться к нулю на , и для практических целей - чем быстрее, тем лучше (причем вейвлет должен быть хорошо локализован и во времени, и по частоте). Для того чтобы было возможно обратное ВП, спектральная функция вейвлета должна удовлетворять еще одному условию

Формула непрерывного обратного вейвлет-преобразования имеет вид

Как видно из (4), исходный сигнал x(t) может быть восстановлен через интегральную сумму тех же базисных функций ψ_ατ(t) с весами в виде вейвлет-спектра сигнала [W_ψx](α,τ). Здесь константа C_ψ (3) выступает как нормирующий коэффициент, аналогичный коэффициенту (2π)^1/2, нормирующему преобразование Фурье.

С целью более эффективного вычисления операторы прямого (1) и обратного (4) ВП могут быть представлены в частотной области [5, 9]. При этом достигается значительное повышение быстродействия цифровых устройств, реализующих ВП, за счет вычисления сверток с помощью эффективных процедур БПФ. Оператор (1) непрерывного прямого ВП может быть определен в частотной области [5 (с.59, 67-68), 9] в виде

где - образ Фурье выбранного исходного вейвлета ψ(t);

- образ Фурье анализируемого процесса x(t).

Оператор (4) непрерывного обратного ВП также может быть определен в частотной области в виде

где - преобразование Фурье от вейвлет-спектра процесса x(t).

Единственным ограничением для данной формы записи операторов (5) и (6) непрерывного ВП, по сравнению с (1) и (4), является требование аналитичности для исследуемого сигнала и применяемого вейвлета [5 (с.67-68)]

т.е. и при f≤0.

Известно большое количество других видов частотно-временного представления сигналов (Табора, Пейджа, Вигнера, Цзуя-Уильямса и т.д.) [10], однако все они (в отличие от ВП) обладают худшими локализующими свойствами в частотно-временной плоскости (имеют место ложные элементы и плохая одновременная различимость дельта-импульсов и тональных сигналов) и не всегда имеют обратное преобразование для точного восстановления исходного временного сигнала. Соответственно, данные методы частотно-временного представления обычно применяются лишь для анализа сигналов, но не для решения задач их обнаружения на фоне помех.

Применение масштабно-временного представления (на основе ВП) к входному процессу x(t) обнаружителя сигналов [11]

где s(t) - обнаруживаемый эхо-сигнал;

n(t) - аддитивная помеха в виде гауссова белого шума,

позволяет (до непосредственной операции согласованной фильтрации) реализовать предварительную «полосовую фильтрацию» вейвлет-спектра принимаемого сигнала, s(t) одновременно в области времени и масштабов (частот) с помощью специального фильтра H(α, τ)

где в качестве масштабно-временного фильтра H(α, τ) выступает двумерная функция специального вида

где - вейвлет-спектр копии излученного сигнала s(t);

A₀ - уровень, задаваемый исходя из условия ,

параметр 0<B<1 выбирается в зависимости от вида частотной модуляции сигнала и условия сохранения заданной доли энергии исходного сигнала , приходящейся на восстановленный сигнал s₁(t) после применения обратного ВП к результату перемножения (фильтрации)

Предварительная фильтрация (8) входного процесса x(t) в масштабно-временной области (для наиболее широко применяемого в гидролокации и радиолокации класса частотно-модулированных сигналов) позволяет добиться значительного выигрыша в помехоустойчивости, по сравнению с классической согласованной фильтрацией или корреляционным приемником [1-4].

Выходное ОСП предлагаемого обнаружителя справедливо записать в виде: , выходное ОСП классической согласованной фильтрации в виде: .

Выигрыш в помехоустойчивости предлагаемого способа обнаружения ЧМС по сравнению с классической согласованной фильтрацией обусловлен уменьшением уровня помех (N₁<N) после «вейвлет-фильтрации» (8) входного процесса, при сохранении примерно неизменной энергии принимаемого сигнала в выходном процессе (при выполнении гипотезы H₁).

Уменьшение уровня спектральной плотности помехи (также, как и ее дисперсии) и, соответственно, увеличение ОСП (характеризующее выигрыш в помехоустойчивости) примерно равно отношению «площадей» в масштабно-временной области, занимаемых вейвлет-спектром входного процесса до «вейвлет-фильтрации» Wx и после «вейвлет-фильтрации» Wx₁

т.к. в случае белого шума его мощность (после ВП) равномерно распределяется по масштабно-временной области в пределах условного «прямоугольника», ограниченного по оси времени τ - длительностью импульса T_S и по оси масштабов α - полосой масштабов Δα_S=α₁-α₂ (однозначно соответствующей спектральной полосе девиации частоты модулированного сигнала Δf_S=f_в-f_н). После фильтрации (8) оставшаяся в выходном процессе x₁(t) часть мощности помехи в масштабно-временной области ограничена площадью носителя фильтрующей функции (α, τ)∈supp{[H(α, τ)}, где H(α, τ)≠0.

Способ обнаружения частотно-модулированных сигналов с фильтрацией в масштабно-временной области [11] включает в себя следующие операции.

1. Вычисление вейвлет-преобразования Wx(α,τ) входного процесса x(t) (наиболее эффективно эта процедура реализуется в частотной области с использованием аналитического вейвлета, в соответствии с оператором (5)):

1.1. выбор исходного вейвлета, ψ(t) вычисление его спектра Фурье , комплексное сопряжение и обнуление отрицательных частот (приведение к аналитическому виду): при f>0 и при f≤0 (в случае выбора комплексного аналитического вейвлета, последняя процедура - обнуления отрицательных частот, необязательна);

1.2. вычисление базиса спектров аналитических вейвлетов путем масштабирования (сжатия) исходного спектра материнского вейвлета: ;

1.3. вычисление спектра Фурье входного процесса ;

1.4. перемножение спектра Фурье входного процесса с сопряженным базисом сжатых спектров аналитических вейвлетов ;

1.5. вычисление обратного преобразования Фурье от результата последнего перемножения: .

2. Вычисление вейвлет-преобразования Ws(α,τ) эталона зондирующего сигнала s(t) (с использованием вычисленного ранее базиса спектров аналитических вейвлетов (в соответствии с п.1.2)):

2.1 вычисление спектра Фурье эталонного сигнала ;

2.2 перемножение спектра Фурье эталонного сигнала с сопряженным базисом сжатых спектров аналитических вейвлетов ;

2.3 вычисление обратного преобразования Фурье от результата последнего перемножения: .

3. Формирование двумерной фильтрующей функции H(α,τ) в масштабно-временной плоскости, вырезающей область значений (α,τ), где модуль комплексного вейвлет-спектра эталона зондирующего сигнала Ws(α,τ) превышает заданный уровень A₀ (13):

4. Перемножение вейвлет-спектра входного процесса и масштабно-временной фильтрующей функции:

.

5. Вычисление обратного вейвлет-преобразования для результата последнего перемножения Wx₁(α,τ) (с использованием вычисленного ранее базиса спектров аналитических вейвлетов (в соответствии с п.1.2)):

5.1 вычисление прямого преобразования Фурье по τ от двумерного вейвлет-спектра ;

5.2 перемножение спектра Фурье с сопряженным базисом спектров аналитических вейвлетов ;

5.3 вычисление обратного преобразования Фурье по f от результата последнего перемножения: ;

5.4 интегрирование по мере (деление на нормирующий коэффициент C_ψ (3), входящий в состав оператора (6), может не производиться, т.к. это не влияет на помехоустойчивость предлагаемого способа обнаружения; интегрирование по мультипликативной мере необходимо лишь в случае экспоненциальной дискретизации масштабных коэффициентов, в случае линейной дискретизации - достаточно провести интегрирование по обычной аддитивной мере

5.5 вычисление реальной части восстановленного процесса (необходимость данной процедуры обусловлена аналитичностью использованного вейвлета ψ(t) и, соответственно, - аналитичностью выходного процесса x₁(t).

Дальнейшие операции по обработке процесса x₁(t) совпадают с классической реализацией метода обнаружения сигнала известной формы на основе согласованной фильтрации.

6. Согласованная фильтрация обнаруживаемого сигнала s(t) известной формы:

6.1. вычисление комплексного спектра Фурье процесса x₁(t);

6.2. вычисление комплексного спектра Фурье эталонного сигнала s(t), и его комплексное сопряжение ;

6.3. перемножение комплексного спектра Фурье с сопряженным спектром Фурье эталона ;

6.4. вычисление обратного преобразования Фурье от результата последнего перемножения: .

7. Выделение (квадратичное детектирование) огибающей отклика согласованного фильтра: (вычисление квадрата модуля отклика СФ y(t)).

8. Сравнение с порогом (выбираемым в зависимости от требуемой вероятности ложной тревоги) и принятие решения об обнаружении сигнала в случае превышения порога (гипотеза H₁), либо о необнаружении - в случае непревышения порога (гипотеза H₀).

Следует отметить, что при использовании огибающей отклика СФ достаточно наблюдать ее амплитуду через интервал времени, приблизительно равный эффективной ширине полосы огибающей [1, с.343].

Заметим также, что операции 1.1 и 1.2 производятся только с вейвлетом ψ(t), операции 2.1, 2.2, 2.3, 3 и 6.2 производятся только с эталонным сигналом s(t), а не с исследуемым входным процессом x(t), и, таким образом, данные операции могут быть проведены заранее, а результаты их расчетов - храниться в ПЗУ.

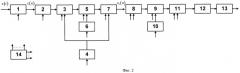
Устройство [11] (прототип), реализующее способ обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области [11], приведено на фиг.1, где:

блок 1 - аналого-цифровой преобразователь (АЦП);

блок 2 - рециркулятор;

блок 3 - вычислитель быстрого преобразования Фурье (БПФ) 1;

блоки 4.1-4.М - комплексные перемножители;

блок 5 - постоянное запоминающее устройство (ПЗУ) 1;

блоки 6.1-6.М - вычислители обратного БПФ;

блок 7 - матричный комплексный перемножитель;

блок 8 - ПЗУ 2;

блоки 9.1-9.М - вычислители БПФ;

блоки 10.1-10.М - комплексные перемножители;

блок 11.1-11.М - вычислители обратного БПФ;

блок 12 - матричный интегратор;

блок 13 - вычислитель БПФ 2;

блок 14 - комплексный перемножитель;

блок 15 - ПЗУ 3;

блок 16 - вычислитель обратного БПФ;

блок 17 - вычислитель квадрата модуля;

блок 18 - пороговое устройство;

блок 19 - управляющее устройство.

Таким образом, устройство обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области (прототип) [11] содержит: аналого-цифровой преобразователь (блок 1), на вход которого подается входной сигнал, выход АЦП соединен с входом рециркулятора (блок 2), выход которого соединен с входом первого вычислителя быстрого преобразования Фурье (блок 3), выход которого соединен с первыми входами M комплексных перемножителей (блоки 4.1-4.М), выходы которых соединены с входами М вычислителей обратного преобразования Фурье (блоки 6.1-6.М), выходы которых соединены с первыми входами матричного комплексного перемножителя (блок 7), выходы которого соединены с входами М вычислителей быстрого преобразования Фурье (блоки 9.1-9.М), выходы которых соединены с первыми входами М комплексных перемножителей (блоки 10.1-10.М), выходы которых соединены с входами М вычислителей обратного преобразования Фурье (блоки 11.1-11.М), выходы которых соединены с входами матричного интегратора (блок 12), выход которого соединен с входом второго вычислителя быстрого преобразования Фурье (блок 13), выход которого соединен с первым входом комплексного перемножителя (блок 14), выход которого соединен с входом вычислителя обратного быстрого преобразования Фурье (блок 16), выход которого соединен с входом вычислителя квадрата модуля (блок 17), выход которого соединен с входом порогового устройства (блок 18), выход которого является выходом устройства; первое постоянное запоминающее устройство (блок 5), выходы которого соединены со вторыми входами М комплексных перемножителей (блоки 4.1-4.М) и со вторыми входами М комплексных перемножителей (блоки 10.1-10.М); второе постоянное запоминающее устройство (блок 8), выход которого соединен со вторым входом матричного комплексного перемножителя (блок 7); третье постоянное запоминающее устройство (блок 15), выход которого соединен со вторым входом комплексного перемножителя (блок 14); управляющее устройство (блок 19), выходы которого соединены с управляющими входами аналого-цифрового преобразователя (блок 1), рециркулятора (блок 2), вычислителей быстрого преобразования Фурье (блоки 3, 9.1-9.М и 13), комплексных перемножителей (блоки 4.1-4.М, 7, 10.1-10.М и 14), вычислителей обратного быстрого преобразования Фурье (блоки 6.1-6.М, 11.1-11.М и 16) и постоянных запоминающих устройств (блоки 5, 8 и 15).

Принцип действия устройства заключается в следующем. На вход устройства поступает реализация входного процесса x(t), которая поступает на вход АЦП (блок 1) с частотой дискретизации, удовлетворяющей требованиям теоремы Котельникова: .

С выхода АЦП (блок 1) дискретные отсчеты поступают на вход рециркулятора (блок 2), где формируется и с каждым новым отсчетом обновляется текущая дискретная выборка x(n) длиной N отсчетов. Длина выборки N определяется длительностью излучаемого сигнала и интервалом дискретизации: . Сформированная текущая дискретная выборка входного процесса x(n) поступает на вход первого вычислителя БПФ (блок 3), с выхода которого комплексный спектр входной реализации поступает одновременно на первые входы М комплексных перемножителей (блоки 4.1-4.М).

С выходов первого ПЗУ (блок 5) считывается М одномерных массивов длиной N отсчетов (вычисленного заранее базиса сжатых спектров аналитических вейвлетов) и поступает на вторые входы комплексных перемножителей (блоки 4.1-4.М), с выходов которых результаты перемножения поступают на входы вычислителей обратного БПФ (блоки 6.1-6.М). Количество масштабов М определяется максимальным значением коэффициента сжатия исходного вейвлета α_max и шагом линейной дискретизации масштаба .

С выходов вычислителей обратного БПФ (блоки 6.1-6.М) результат вейвлет-преобразования входного процесса Wx(m, n) в виде двумерного массива размером М масштабов на N сдвигов поступает на первые входы матричного комплексного перемножителя (блок 7).

С выхода второго ПЗУ (блок 8) считывается вычисленный заранее двумерный массив фильтрующей функции H(m, n) (в масштабно-временной плоскости) размером М масштабов на N сдвигов и поступает на второй вход матричного комплексного перемножителя (блок 7), с выходов которого М одномерных массивов длиной N отсчетов результата перемножения (т.е. фильтрации в масштабно-временной плоскости) Wx₁(m, n) поступают на входы вычислителей БПФ (блоки 9.1-9.М), с выходов которых результаты БПФ поступают на первые входы М комплексных перемножителей (блоки 10.1-10.М).

С выходов первого ПЗУ (блок 5) считывается М одномерных массивов длиной N отсчетов (вычисленного заранее базиса сжатых спектров аналитических вейвлетов) и поступает на вторые входы комплексных перемножителей (блоки 10.1-10.М), с выходов которых результаты перемножения поступают на входы вычислителей обратного БПФ (блоки 11.1-11.М), с выходов которых результаты обратного БПФ поступают на входы матричного интегратора (блок 12), где производится интегральное суммирование по масштабу m.

С выхода матричного интегратора (блок 12) временная реализация отфильтрованного в масштабно-временной области процесса x₁(n) поступает на вход второго вычислителя БПФ (блок 13), с выхода которого комплексный спектр поступает на первый вход комплексного перемножителя (блок 14).

Из третьего ПЗУ (блок 15) считывается вычисленный заранее сопряженный комплексный спектр эталонного сигнала и поступает на второй вход комплексного перемножителя (блок 14), с выхода которого результат перемножения поступает на вход вычислителя обратного БПФ (блок 16). С выхода вычислителя обратного БПФ (блок 16) отклик согласованного фильтра y(n) поступает на вход вычислителя квадрата модуля (блок 17), с выхода которого выделенная огибающая поступает на вход порогового устройства (блок 18), выход которого является выходом устройства.

Устройство управления (блок 19) осуществляет синхронизацию работы: аналого-цифрового преобразователя (блок 1), рециркулятора (блок 2), вычислителей быстрого преобразования Фурье (блоки 3, 9.1-9.М и 13), комплексных перемножителей (блоки 4.1-4.М, 7, 10.1-10.М и 14), вычислителей обратного быстрого преобразования Фурье (блоки 6.1-6.М, 11.1-11.М и 16) и постоянных запоминающих устройств (блоки 5, 8 и 15).

Однако данное устройство [11] (прототип), реализующее способ обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией, в масштабно-временной области [11], обладает следующим недостатком. Цифровая реализация операций вычисления прямого и обратного «непрерывного» (избыточного дискретного) вейвлет-преобразования с произвольно мелким шагом дискретизации масштабных коэффициентов α_m=α₀ ^m, 1<α₀<2, позволяющим анализировать сигнал с произвольной точностью измерения масштабов, не эффективна с точки зрения требуемых быстродействия и вычислительных и аппаратурных затрат.

Так, для цифровой реализации прямого и обратного НВП (основных составляющих операции предварительной фильтрации полезного сигнала на фоне помех в масштабно-временной области [11]) входной выборки длиной N отсчетов требуются следующие цифровые ресурсы:

- в памяти ПЗУ (блок 5) должны храниться М вычисленных заранее сжатых копий спектра исходного вейвлета - каждая длиной N отсчетов (уместно заметить, что для их предварительного вычисления требуется провести М операций масштабирования (сжатия) спектра исходного вейвлета и, соответственно, столько же интерполяционных процедур);

- в памяти ПЗУ (блок 8) должен храниться вычисленный заранее двумерный массив фильтрующей функции H(m, n) (в масштабно-временной плоскости) размером М масштабов на N сдвигов;

- для реализации вычисления прямого вейвлет-преобразования с произвольным дискретным шагом масштаба в спектральной области требуется: одна операция прямого БПФ (блок 3) и М операций обратного БПФ (блоки 6.1-6.М), или соответственно примерно операций комплексного умножения (с учетом того, что одна операция БПФ для сигнала длиной N отсчетов требует комплексных умножений [12 (с.647)]); плюс MN операций комплексного умножения в перемножителях (блоки 4.1-4.М);

- для реализации перемножения фильтрующей функции H(m, n) и результата вейвлет-преобразования входного процесса Wx(m, n) требуется MN операций комплексного умножения (блоки 4.1-4.М);

- для реализации вычисления обратного вейвлет-преобразования с произвольным дискретным шагом масштаба в спектральной области требуется: М операций прямого БПФ (блоки 9.1-9.М) и М операций обратного БПФ (блоки 11.1-11.М), или соответственно, примерно MNlog₂N операций комплексного умножения; плюс MN операций комплексного умножения в перемножителях (блоки 10.1-10.М);

Итого:

- требуемый объем памяти ПЗУ - 2 MN;

- требуемый объем вычислений - операций комплексного умножения.

Ниже предлагается новое устройство, реализующее способ обнаружения сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области, на основе использования вычислителей прямого и обратного дискретного вейвлет-преобразования (ДВП) с шагом дискретизации масштабных коэффициентов, равным 2, значительно более эффективное с точки зрения быстродействия, вычислительных и аппаратурных затрат, чем прототип.

При этом помехоустойчивость предлагаемого нового обнаружителя, как, показало моделирование в среде MathCadl3, практически полностью совпадает с помехоустойчивостью устройства-прототипа [11], т.е. обладает аналогичным выигрышем (11) относительно классического согласованного фильтра.

Теоретические основы быстрого алгоритма дискретного вейвлет-преобразования

При дискретном вейвлет-преобразовании необходимая дискретизация значений параметров α и τ при сохранении возможности восстановления сигнала из его вейвлет-преобразования должна осуществляться следующим образом

где m, n ∈ Z; α₀>1; τ₀≠0.

Параметр сдвига зависит от параметра масштаба. С увеличением масштаба увеличивается и размер шага сдвига. При шаге сдвига τ₀=1, соответствующем одному отсчету, базис вейвлет-функций представляется в виде

При некотором, весьма специфичном, выборе вейвлета ψ и исходных значений α₀, τ₀ дискретный набор функций ψ_ατ, образует ортонормированный базис в гильбертовом пространстве [5].

В частности, при дискретном ВП, без потери общности, выбирают α₀=2 и τ₀=1

Т.е. в цифровом виде при ДВП минимальный шаг логарифмического масштаба параметра сжатия (или его основание) равен двум, а минимальный шаг параметра сдвига по времени - единице (т.е. одному отсчету).

Именно для данного способа дискретизации параметров сжатия и сдвига разработаны все известные эффективные алгоритмы быстрого дискретного вейвлет-преобразования (DWT - discrete wavelet transform) [5-8]. В этом случае для сжатия исходного сигнала в 2^m раза достаточно произвести соответствующее количество раз прореживание четных или нечетных временных отсчетов. Именно таким способом реализуется масштабирование сигналов в алгоритмах быстрого дискретного вейвлет-преобразования.

В отличие от теории непрерывного ВП, в теории дискретного ортогонального ВП, а точнее, в теории кратномасштабного анализа [5], помимо функции вейвлета ψ(t) вводится еще одно важное понятие - так называемая скейлинг-функция (или масштабирующая функция) φ(t). В литературе масштабирующую функцию φ(t) иногда называют «отцовским» вейвлетом по аналогии с материнским вейвлетом ψ(t).

Функциям вейвлета и скейлинг-функции в теории ДВП ставятся в соответствие дискретные последовательности g_n и h_n. Функции ψ(t), φ(t) и последовательности g_n, h_n связаны между собой следующими основными соотношениями

При вычислении ДВП оказывается возможным итеративное вычисление дискретных вейвлет-коэффициентов c_j,k и d_j,k, без непосредственного использования функций отцовского φ(t) и материнского вейвлета ψ(t}. Для произвольного этапа разложения j можно записать

получив таким образом полностью дискретный процесс декомпозиции сигнала (прямого ДВП). Последовательности h_n и g_n по сути являются импульсными характеристиками цифровых НЧ- и ВЧ-фильтров. При этом коэффициенты аппроксимации c_j,k и детализации d_j,k. имеют «половинную» длину по сравнению с c_j-1,k.

Для матричного описания процедуры ДВП через вектор v^j обозначают последовательность конечной длины c_j,n для некоторого номера масштаба j (или этапа вычисления ДВП). На каждом этапе ДВП этот вектор преобразуется в вектор V^j+1, который содержит последовательности c_j+1,n и d_j+1,n, каждая из которых половинной длины. Преобразование может быть записано в виде (18) матричного умножения v^j+1=M_jv^j, где M_j - квадратная матрица, состоящая из нулей и элементов h_n, умноженных на . В силу свойств h_n, матрица M_j является ортонормированной и обратная ей матрица равна транспонированной.

В качестве иллюстрации можно рассмотреть следующий пример. Возьмем фильтры g_n и h_n длиной L=4, последовательность сигнала c₀ длиной N=8, а в качестве начального значения масштаба - j=0.

Тогда операция матрично-векторного умножения может быть представлена в виде

Последовательность g_n можно получить из h_n по формуле: g_n=(-1)ⁿh_-n+2L+1 переписать (18) в виде

Таким образом, операция (19) - это один шаг ДВП. Полный алгоритм ДВП заключается в итеративном умножении верхней половины вектора v^j+1 на квадратную матрицу M_j+1, размер которой 2^D-j. Эта процедура повторяется D раз, пока длина вектора не станет равной одному отсчету.

Полное разложение исходного сигнала c_0,n длиной N=2^D на вейвлет-коэффициенты d_j,n потребует D аналогичных матричных умножений (для j=0, …, D-1 этапов ДВП). Необходимо отметить, что общее количество элементарных операций умножения в алгоритме ДВП зависит от длины L выбранных последовательностей h_n, g_n, т.е. от выбранного типа вейвлета и его порядка. Как правило, для наиболее известных дискретных вейвлетов (Хаара, Добеши - различных порядков) длина L последовательности h_n значительно меньше длины выборки N анализируемого сигнала. Наиболее экономичным в этом смысле является вейвлет Хаара длиной всего в два отсчета.

Окончательный результат ДВП содержит N вейвлет-коэффициентов: N - 1 коэффициентов деталей d_j,n и один коэффициент аппроксимации c_J,0. Обычно результат одномерного ДВП записывают одной строкой длиной в N коэффициентов (в частности, в приложениях MathCad и MathLab). Для рассмотренного примера результат ДВП будет иметь вид

[d_1,0, d_1,1, d_1,2, d_1,3; d_2,0, d_2,1; d_3,0; c_3,0].

Коэффициент аппроксимации последнего уровня c_J,0 ходим для возможности начала реализации итеративного вычисления обратного ДВП.

Обратное ДВП можно описать с помощью умножения v^j+1 обратную матрицу

В иностранной литературе рассмотренный быстрый алгоритм вычисления ДВП связывают с работами С.Малла (S.Mallat) [5]. Быстрый алгоритм Малла дискретного вейвлет-преобразования исходного сигнала длиной N отсчетов реализуется в D=log₂ N этапов и требует всего лишь 2NL умножений.

Сущность предлагаемого устройства

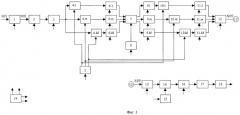
Предлагаемое устройство - обнаружитель сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области на основе дискретного вейвлет-преобразования - приведено на фиг.2, где:

блок 1 - аналого-цифровой преобразователь (АЦП);

блок 2 - рециркулятор;

блок 3 - вычислитель дискретного вейвлет-преобразования (ДВП);

блок 4 - постоянное запоминающее устройство (ПЗУ) 1;

блок 5 - перемножитель;

блок 6 - ПЗУ 2;

блок 7 - вычислитель обратного ДВП;

блок 8 - вычислитель БПФ 2;

блок 9 - комплексный перемножитель;

блок 10 - ПЗУ 3;

блок 11 - вычислитель обратного БПФ;

блок 12 - вычислитель квадрата модуля;

блок 13 - пороговое устройство;

блок 14 - управляющее устройство.

Таким образом, обнаружитель сложных широкополосных частотно-модулированных сигналов с фильтрацией в масштабно-временной области на основе дискретного вейвлет-преобразования содержит: аналого-цифровой преобразователь (блок 1), на вход которого подается входной сигнал, выход аналого-цифрового преобразователя соединен с входом рециркулятора (блок 2), выход которого соединен с первым входом вычислителя ДВП (блок 3), выход которого соединен с первым входом перемножителя (блок 5), выход которого соединен с первым входом вычислителя обратного ДВП (блок 7), выход которого соединен с входом вычислителя быстрого преобразования Фурье (блок 8), выход которого соединен с первым входом комплексного перемножителя (блок 9), выход которого соединен с входом вычислителя обратного быстрого преобразования Фурье (блок 11), выход которого соединен с входом вычислителя квадрата модуля (блок 12), выход которого соединен с входом порогового устройства (блок 13), выход которого является выходом устройства; первое постоянное запоминающее устройство (блок 4), выход которого соединен со вторыми входами вычислителя ДВП (блок 3) и вычислителя обратного ДВП (блок 7); второе постоянное запоминающее устройство (блок 6), выход которого соединен со вторым входом перемножителя (блок 5); третье постоянное запоминающее устройство (блок 10), выход которого соединен со вторым входом комплексного перемножителя (блок 9); управляющее устройство; (блок 14), выходы которого соединены с управляющими входами аналого-цифрового преобразователя (блок 1), рециркулятора (блок 2), вычислителя ДВП (блок 3), перемножителя (блок 5), вычислителя обратного ДВП (блок 7), вычислителя быстрого преобразования Фурье (блок 8), комплексного перемножителя (блок 9), вычислителя обратного быстрого преобразования Фурье (блок 11) и постоянных запоминающих устройств (блоки 4, 6 и 10).

Принцип действия устройства заключается в следующем. На вход устройс