Способ определения гидродинамических параметров математической модели движения судна
Иллюстрации
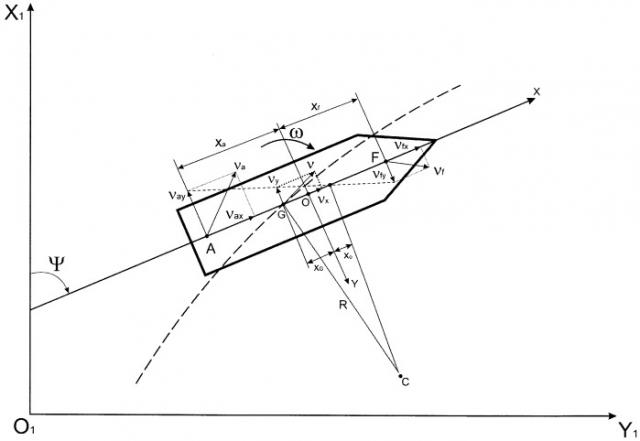
Показать всеИзобретение относится к судовождению и может быть использовано для прогнозирования движения судна при маневрировании. Используют условно носовую и кормовую точки. Носовая и кормовая точки расположены на диаметральной плоскости судна. Измеряют в реальном масштабе времени координаты носовой и кормовой точек. Измерение координат точек проводят с помощью приемников СНС и с дифференциальными поправками. На основании результатов измерений координат этих точек определяют текущие значения кинематических параметров движения судна: линейных скоростей носовой F (υf) и кормовой A (υa) точек и их продольных (υfx, υax) и поперечных (υfy, υay) составляющих в подвижной системе координат ZX0Y, связанной с судном; абсциссы центра вращения (х0) в подвижной системе координат ZX0Y, связанной с судном; проекции вектора линейной скорости в центре тяжести на поперечную ось 0Y (υy); линейной скорости центра тяжести судна (υ); радиуса кривизны траектории центра тяжести судна (R); угловой скорости судна (ω). Полученные данные используют для вычисления текущих значений гидродинамических параметров математической модели движения судна. На базе математической модели выполняют компьютерное моделирование с целью прогнозирования движения судна при маневрировании. Изобретение позволяет повысить точность прогнозирования движения судна при маневрировании на базе адекватной математической модели его движения. 2 з.п. ф-лы, 1 ил.
Реферат
Изобретение относится к области судовождения и может быть использовано для прогнозирования движения судна при маневрировании.
Известен способ определения параметров математической модели движения судна (пат. РФ №2197016, опубл. 20.09.2002), заключающийся в том, что при малых отклонениях руля измеряют угловую скорость судна и начинают интегрировать ее по времени, измеряют путевой угол, запоминают и для получения значения угла курса суммируют оба сигнала, при угле перекладки руля больше заданной величины измеряют фазовые координаты состояния судна, в качестве которых используют угол перекладки руля, угловую скорость судна, путевой угол и угол дрейфа, который формируют в виде алгебраической суммы путевого угла и угла курса, запоминают их в текущий момент времени, подают на вход электронной модели движения судна, формируют разность измеренной угловой скорости судна с полученным на выходе электронной модели сигналом угловой скорости судна, формируют разность вычисленного сигнала угла дрейфа и сигнала угла дрейфа, полученного на выходе электронной модели движения судна, формируют модули этих разностей и минимизируют их путем изменения первого коэффициента математической модели движения судна в электронной модели движения судна, после минимизации модулей разностей измененное значение первого коэффициента математической модели движения судна фиксируют в электронной модели движения судна, сформированные модули разностей вновь минимизируют, путем изменения второго коэффициента математической модели движения судна, после минимизации модулей разностей измененное значение второго коэффициента математической модели движения судна фиксируют в электронной модели движения судна и повторяют процесс уточнения третьего, четвертого, … последнего коэффициента математической модели движения судна.
Недостатком данного способа является то, что параметры математической модели движения судна определяются не единовременно, а поочередно, что, во-первых, делает недопустимо продолжительным сам процесс определения параметров модели (их количество зависит от степени адекватности математической модели и возрастает с ее ростом, может быть равно 10-15 и более), во вторых, при определении рассматриваемых в данный момент параметров, значения определенных ранее параметров, по ряду причин, могут измениться [1], [2], [3], [4], [5]. Растянутость во времени процедуры определения параметров математической модели движения судна приводит к потере адекватности большей части их значений в заданный момент времени, что приводит в итоге и к неадекватности самой математической модели движения судна, и поэтому она не может быть использована для корректного прогнозирования движения судна при выполнении маневрирования.
Известен способ экспериментального определения коэффициентов математической модели движения судна (пат. РФ №2151713, опубл. 27.06.2000), основанный на использовании измеряемого с помощью приемников спутниковой навигационной системы сигнала бокового сноса, электронной модели, соответствующей полной математической модели движения судна, а также на использовании двухмерного критерия с переменными весовыми коэффициентами, который необходим для подстройки параметров. Однако способ не позволяет достаточно точно определить коэффициенты математической модели движения судна, что связано с получением довольно грубого значения текущего угла дрейфа. Кроме того, способу присущ тот же недостаток, что и для патента №2197016, заключающийся в поочередном, а не в единовременном определении параметров математической модели движения судна. Данный способ экспериментального определения коэффициентов математической модели движения судна наиболее близок к предлагаемому и принят за прототип.
Технический результат, на достижение которого направлено заявляемое изобретение, состоит в одновременном определении всех параметров математической модели движения судна в непрерывном режиме и, как следствие, повышении точности прогнозирования движения судна при выполнении им маневрирования с использованием компьютерного моделирования на базе адекватной математической модели движения судна.
Для достижения указанного технического результата в способе определения гидродинамических параметров математической модели движения судна, включающем использование электронной модели движения судна, измерение координат судна с помощью приемников спутниковой навигационной системы (СНС), используют две разнесенные по длине диаметральной плоскости (ДП) судна носовую и кормовую точки, координаты которых используют в качестве координат судна и на их основе определяют текущие значения кинематических параметров движения судна:
- линейных скоростей носовой F (υf) и кормовой А (υа) точек и их продольных (υfx, υax) и поперечных составляющих (υfy, υау) в подвижной системе координат ZX0Y, связанной с судном;
- абсциссы центра вращения (х0) в подвижной системе координат ZX0Y, связанной с судном;
- проекции вектора линейной скорости в центре тяжести (ЦТ) на поперечную ось 0Y (υy);
- линейной скорости центра тяжести судна (υ);
- радиуса кривизны траектории ЦТ судна (R);
- угловой скорости судна (ω);
на основе значений кинематических параметров вычисляют текущие значения гидродинамических параметров математической модели движения судна, на базе последней выполняют компьютерное моделирование движения судна. Кроме того, измерение координат носовой и кормовой точек осуществляют с дифференциальными поправками в реальном масштабе времени, продольные и поперечные составляющие линейных скоростей носовой (υfx, υfy) и кормовой (υax, υау) точек судна в подвижной системе координат ZX0Y, связанной с судном, рассчитывают с учетом воздействия на судно течения в районе маневрирования.
Благодаря наличию этих признаков возможно единовременное определение параметров математической модели движения судна, что позволяет с высокой точностью прогнозировать любой маневр до его выполнения.
Предлагаемый способ определения гидродинамических параметров математической модели движения судна иллюстрируется чертежом, представленным на фигуре.
Способ заключается в следующем. Математическая модель движения судна, используемая для компьютерного моделирования при прогнозировании движения судна в процессе маневрирования, представляет собой систему дифференциальных уравнений, общий вид которых с учетом известных условностей [1], [2], [3], [4], [5] следующий:
;
;
;
;
;
где υx, υy - проекции вектора линейной скорости в ЦТ судна на продольную 0Х и поперечную 0Y оси соответственно;
Ψ - курс судна;
X1, Y1 - координаты ЦТ судна в неподвижной системе координат X101Y1;
C1, C2, C3, … - параметры математической модели, численные значения которых определяются в зависимости от геометрических элементов погруженной части корпуса судна, они постоянны при данном состоянии загрузки последнего [3], [4], [5].
В процессе движения судна с помощью СНС с дифференциальными поправками определяют координаты носовой (x1f, y1f) и кормовой (x1а, y1а) точек судна в неподвижной системе координат X101Y1 и рассчитывают продольные и поперечные составляющие линейных скоростей носовой (υfx1, υfy1) и кормовой (υax1, υay1) точек с использованием известных зависимостей:
.
Далее рассчитывают продольные и поперечные составляющие линейных скоростей носовой (υfx, υfy) и кормовой (υax, υay) точек судна в подвижной системе координат ZX0Y, связанной с судном, с учетом воздействия на судно течения в районе маневрирования:
;
;
где υst - скорость течения;
qst - направление течения.
Очевидно, что продольная составляющая линейной скорости судна в любой заданной точке, расположенной на ДП, будет иметь одно значение, следовательно, можно считать, что
Используя значения абсциссы носовой точки в подвижной системе координат ZX0Y (xf) и абсциссы кормовой точки в той же системе координат (xа), а также поперечные составляющие линейных скоростей в носовой (υfy) и кормовой (υау) точках, определенных с использованием зависимостей (3), рассчитываем абсциссу центра вращения судна (фиг.) x0 [3], [4], [5] по формуле:
Поперечная составляющая линейной скорости в ЦТ судна определяется по формуле, полученной из фиг., а именно:
Определяем значение линейной скорости в ЦТ судна, используя зависимость
и радиус кривизны траектории ЦТ судна по формуле
Известные значения радиуса R и скорости υ позволяют рассчитать угловую скорость судна, т.е.
Значения коэффициентов C1, C2, C3, … рассчитывают только при изменении состояния загрузки судна [1], [2], [3], [5]. Так как состояние загрузки судна в процессе маневрирования не меняется, значения C1, C2, C3, … принимаются постоянными, рассчитанными на момент последнего изменения состояния загрузки судна.
Таким образом, определяют все гидродинамические параметры математической модели движения судна, входящие в правые части дифференциальных уравнений (1). Вычислив правые части уравнений (1), можно в любой заданный момент времени рассчитать значения параметров, характеризующих движение судна при выполнении маневрирования, а именно υх, υy, ω, ψ, x1, x2, что позволяет прогнозировать любой маневр до его выполнения с использованием методов компьютерного моделирования.
Литература
1. Басин A.M. Ходкость и управляемость судов / A.M.Басин. - М.: Транспорт, 1967. - 255 с.
2. Васильев А.В. Управляемость судов: учеб. пособие / А.В.Васильев. - Л.: Судостроение, 1989. - 328 с.
3. Гофман А.Д. Движительно-рулевой комплекс и маневрирование судна: справочник / А.Д.Гофман. - Л.: Судостроение, 1988. - 360 с.
4. Соболев Г.В. Управляемость корабля и автоматизация судовождения / Г.В.Соболев. - Л.: Судостроение, 1976. - 478 с.
5. Справочник по теории корабля. В 3 т. Т.3: Управляемость водоизмещающих судов. Гидродинамика судов с динамическими принципами поддержания / под ред. Я.И.Войткунского. - Л.: Судостроение, 1985. - 544 с.
1. Способ определения гидродинамических параметров математической модели движения судна, включающий использование электронной модели движения судна, измерение координат судна с помощью приемников спутниковой навигационной системы (СНС), отличающийся тем, что используют две разнесенные по длине диаметральной плоскости (ДП) судна носовую и кормовую точки, координаты которых используют в качестве координат судна, на основе которых определяют текущие значения кинематических параметров движения судна:- линейных скоростей носовой F (υf) и кормовой А (υа) точек и их продольных (υfx, υах) и поперечных (υfy, υay) составляющих в подвижной системе координат ZX0Y, связанной с судном;- абсциссы центра вращения (х0) в подвижной системе координат ZX0Y, связанной с судном;- проекции вектора линейной скорости в центре тяжести на поперечную ось 0Y (υу);- линейной скорости центра тяжести судна (υ);- радиуса кривизны траектории ЦТ судна (R);- угловой скорости судна (ω);на основе значений кинематических параметров вычисляют текущие значения гидродинамических параметров математической модели движения судна, на базе последней выполняют компьютерное моделирование движения судна.
2. Способ по п.1, отличающийся тем, что измерение координат носовой и кормовой точек осуществляют с дифференциальными поправками в реальном масштабе времени.
3. Способ по п.1, отличающийся тем, что продольные и поперечные составляющие линейных скоростей носовой (υfx, υax) и кормовой (υax, υay) точек судна в подвижной системе координат ZX0Y, связанной с судном, рассчитывают с учетом воздействия на судно течения в районе маневрирования.