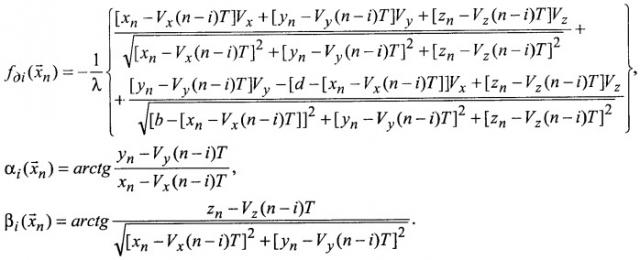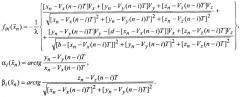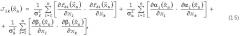Устройство для определения координат движущихся целей

Устройство для определения координат движущихся целей

Иллюстрации

Показать все

Реферат

Изобретение относится к радиолокации, в частности к методам восстановления траектории цели в бистатической радиолокации с обнаружением "на просвет", например, в наземно-космических радиолокационных комплексах.

Известно устройство для определения параметров движения цели, патент РФ №2124220, МПК G01S 13/06, опубликован 27.12.1998 г., авторы: Бляхман А.Б., Ковалев Ф.Н., Рындык А.Г. Работа устройства основана на приеме зондирующего сигнала и сигнала вторичного излучения цели, выделения низкочастотного сигнала биений путем детектирования интерференционного сигнала (суммы прямого сигнала передатчика и отраженного от цели сигнала), измерении доплеровской частоты и направления прихода отраженного от цели сигнала по интерференционному сигналу, экстраполяции измеряемых первичных параметров и вычислении момента времени пересечения целью линии базы. Применение ряда операций и преобразований позволяет определять местоположение цели до пересечения ею линии базы. Это достигается за счет экстраполяции измеряемых функциональных зависимостей f_∂(t) - частоты Доплера от времени и α(t) - углового направления на цель от времени, и, тем самым, определения экстраполированного момента времени пересечения целью линии базы из условия равенства нулю экстраполированных функциональных зависимостей. Таким образом, используя несколько измеряемых значений f_∂ и α, в этом способе производится экстраполяция зависимостей f_∂(t) и α(t), по которым определяется момент времени пересечения целью линии базы до прихода к ней цели и во время нахождения ее в зоне режекции доплеровских фильтров. Пространственные координаты цели однозначно находятся как координаты точки пересечения поверхности положения (поверхности равных фаз или суммарных дальностей) и линии направления на цель из приемной позиции (линии пеленга).

Описанное устройство характеризуется значительным ростом ошибки измерения дальности до цели в окрестности линии базы системы, что связано с высокой чувствительностью измерений к отклонениям угловой координаты и отклонениям поверхности положения (поверхности равных фаз или суммарных дальностей) в непосредственной близости от линии базы, а также недостаточно высокой точностью определения местоположения цели по сравнению с потенциально достижимой точностью.

В качестве прототипа принято устройство для определения параметров движения объекта, патент РФ №2154840, МПК G01S 13/06, опубликован 20.08.2000 г., авторы: Бляхман А.Б, Ковалев Ф.Н., Рындык А.Г., Сидоров С.Б. Данное устройство содержит передающую позицию и в удаленной от нее точке приемную позицию, состоящую из антенны, соединенной с приемным устройством (включающим в себя два канала, каждый из которых состоит из последовательного соединения приемника, детектора и фильтра низкой частоты (ФНЧ)), выход которого соединен с входами блока измерения доплеровской частоты и входами блока измерения направления прихода отраженного от цели сигнала (по интерференционному сигналу), блока экстраполяции измеряемых параметров, один из входов которого соединен с выходом блока измерения доплеровской частоты, второй вход - с выходом блока измерения направления прихода отраженного от цели сигнала, а выход блока экстраполяции измеряемых параметров соединен с входом блока вычисления момента времени пересечения целью линии базы, блока определения поверхности положения, один из входов которого соединен с выходом блока вычисления момента времени пересечения целью линии базы, второй вход - с выходом блока экстраполяции измеряемых параметров, а выход - с одним из входов блока вычисления начального приближения траекторных параметров, другой вход которого соединен с выходом блока измерения направления прихода отраженного от цели сигнала, при этом выход блока вычисления начального приближения траекторных параметров соединен с входом блока конечного вычисления (уточнения) траекторных параметров, другие входы которого соединены соответственно с выходом блока определения статистических характеристик ошибок измерения доплеровской частоты и направления прихода отраженного от цели сигнала, а также выходом блока измерения направления прихода отраженного от цели сигнала и выходом блока измерения доплеровской частоты, при этом выходом всего устройства является выход блока конечного вычисления траекторных параметров.

В этом устройстве осуществляется прием зондирующего сигнала и сигнала вторичного излучения цели, выделение из них низкочастотного сигнала биений путем детектирования интерференционного сигнала, измерение доплеровской частоты (частоты биений) сигнала, например путем измерения моментов времени переходов его напряжения через нуль, измерение направления прихода отраженного от цели сигнала (по интерференционному сигналу), например моноимпульсным методом по соотношению амплитуд интерференционного сигнала в парциальных каналах, фазовым способом или сканированием луча антенны по максимуму значений огибающей сигнала на выходе фильтра низкой частоты [Теоретические основы радиолокации / под ред. Я.Д.Ширмана. М.: Советское Радио, 1970. С.274-310].

Определение параметров движения цели в этом устройстве условно можно разделить на два этапа. На первом из них по измеренным значениям частоты Доплера f_∂(t) и угловой координаты цели α(t) (азимута цели) происходит предварительная оценка местоположения цели, другими словами, находится начальное приближение траекторных параметров, а на втором - уточнение ее в соответствии с критерием максимального правдоподобия.

До пересечения целью линии базы предварительная оценка траекторных параметров осуществляется путем экстраполяции измеряемых функциональных зависимостей f_∂(t) - частоты Доплера от времени и α(t) - углового направления на цель от времени, определения момента времени пересечения целью линии базы из условия равенства нулю экстраполированных функциональных зависимостей, оценки суммарной дальности и нахождения точки пересечения поверхности положения (поверхности равных суммарных дальностей) и направления на цель (линии пеленга цели). После пересечения целью линии базы оценка суммарной дальности может быть получена путем непосредственного интегрирования измеренной зависимости f_∂(f).

Для получения уточненных в соответствии с критерием максимального правдоподобия оценок траекторных параметров цели может использоваться, например, итерационный алгоритм. При этом предварительно вычисляются статистические характеристики ошибок измерения первичных параметров (доплеровской частоты и направления прихода отраженного от цели сигнала).

Устройство, взятое в качестве прототипа, характеризуется резким ухудшением точности определения координат цели экстраполяционным алгоритмом с предварительной оценкой суммарной дальности при изменении высоты полета цели в процессе ее движения. При увеличении наклона траектории в вертикальной плоскости момент, когда цель находится на кратчайшем расстоянии от линии базы, все более отличается от момента, когда азимут цели равен нулю. А при движении цели по траектории, нормальной к плоскости (x, y), азимут вообще не обращается в ноль. При этом точность оценок начального приближения может оказаться недостаточной для схождения итерационной процедуры к глобальному максимуму функции правдоподобия.

Предлагаемое устройство позволяет устранить этот недостаток. Это достигается тем, что в устройство, содержащее передающую позицию и в удаленной от нее точке приемную позицию, состоящую из антенны, соединенной с приемным устройством азимутального угломерного канала, выходы которого соединены с входами блока измерения доплеровской частоты и входами блока измерения направления прихода отраженного от цели сигнала в азимутальной плоскости, блока экстраполяции измеряемых параметров, один из входов которого соединен с выходом блока измерения доплеровской частоты, а выход блока экстраполяции измеряемых параметров соединен с входом блока вычисления момента времени пересечения целью линии базы, блока определения поверхности положения, один из входов которого соединен с выходом блока вычисления момента времени пересечения целью линии базы, второй вход - с выходом блока экстраполяции измеряемых параметров, а выход - с одним из входов блока вычисления начального приближения траекторных параметров, при этом входы блока вычисления траекторных параметров соединены соответственно с блоком определения статистических характеристик ошибок измерения доплеровской частоты и направления прихода отраженного от цели сигнала, с блоком измерения доплеровской частоты, блоком измерения направления прихода отраженного от цели сигнала в азимутальной плоскости, причем выходом всего устройства является выход блока вычисления траекторных параметров, введены антенна, формирующая лучи в угломестной плоскости, приемное устройство угломестного угломерного канала, блок измерения направления прихода отраженного от цели сигнала в угломестной плоскости, блок пересчета углов для повернутой системы координат и блок пересчета траекторных параметров из повернутой системы координат в исходную систему координат, причем антенна, формирующая лучи в угломестной плоскости, соединена с приемным устройством угломестного угломерного канала, которое, в свою очередь, последовательно соединено с блоком измерения направления прихода отраженного от цели сигнала в угломестной плоскости и блоком пересчета углов для повернутой системы координат, другой вход которого соединен с выходом блока измерения направления прихода отраженного от цели сигнала в азимутальной плоскости, а два выхода соединены с входами блока экстраполяции измеряемых параметров и блока вычисления начального приближения траекторных параметров; входы блока определения статистических характеристик ошибок измерения доплеровской частоты и направления прихода отраженного от цели сигнала соединены с выходами блоков измерения направления прихода отраженного от цели сигнала в азимутальной и угломестной плоскостях соответственно и выходом блока измерения доплеровской частоты; вход блока пересчета траекторных параметров из повернутой системы координат в исходную систему координат соединен с выходом блока вычисления начального приближения траекторных параметров, а выход - с блоком вычисления траекторных параметров; выход блока измерения направления прихода отраженного от цели сигнала в угломестной плоскости соединен с блоком вычисления траекторных параметров.

Применение новых блоков и связей позволило строить с приемлемой точностью траектории, имеющие произвольный наклон к плоскости (x, y). Это достигается за счет использования информации об угломестном положении цели (возможность измерения угла места появляется после введения дополнительного блока), а также путем осуществления дополнительных преобразований над первичными измеряемыми параметрами (азимутом и углом места цели) и начальными приближенными значениями координат цели.

Сравнение предложенного технического решения с другими известными источниками патентной и научно-технической документации показывают, что в них отсутствуют технические решения, позволяющие в бистатической просветной радиолокационной системе (БРЛС) достигнуть такого технического результата - определения местоположения цели, траектория которой имеет произвольный наклон к горизонтальной плоскости (x, y), с точностью, близкой к потенциально достижимой точности.

Для более полного понимания изложенной сущности заявляемого устройства следует обратиться к нижеследующему описанию и чертежам, иллюстрирующим изобретение.

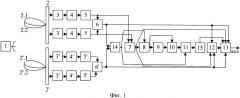
На фиг.1 представлена функциональная схема заявляемого устройства, когда определение направления прихода отраженного от цели сигнала осуществляется моноимпульсным методом с двумя пространственными каналами. На чертеже введены следующие обозначения:

1 - передающая позиция;

2 - антенна приемной позиции, формирующая лучи (2.1 и 2.2) в азимутальной плоскости;

2′ - антенна приемной позиции, формирующая лучи (2′.1 и 2′.2) в угломестной плоскости;

3 и 3′ - приемник;

4 и 4′ - детектор;

5 и 5′ - ФНЧ;

6 - блок измерения направления прихода отраженного от цели сигнала в азимутальной плоскости;

6′ - блок измерения направления прихода отраженного от цели сигнала в угломестной плоскости;

7 - блок измерения доплеровской частоты f_∂;

8 - блок экстраполяции измеряемых параметров (зависимостей доплеровской частоты и угловых координат цели α, β от времени);

9 - блок вычисления момента времени пересечения целью линии базы;

10 - блок определения поверхности положения;

11 - блок вычисления начального приближения траекторных параметров;

12 - блок определения статистических характеристик ошибок измерения доплеровской частоты и направления прихода отраженного от цели сигнала;

13 - блок вычисления траекторных параметров;

14 - блок пересчета азимута и угла места цели (α, β) для повернутой системы координат;

15 - блок пересчета траекторных параметров из повернутой системы координат в исходную систему координат.

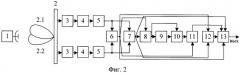
На фиг.2 представлена функциональная схема устройства-прототипа с определением направления прихода отраженного от цели сигнала моноимпульсным методом с двумя пространственными каналами, где использованы те же, что и на фиг.1, обозначения.

На фиг.3 приведены основные геометрические соотношения для предлагаемого устройства, показаны связанная с ним декартова система координат xyz и возможная движущаяся цель. На фиг.3 обозначено:

П - передающая позиция (расположена в точке с координатами (b;0;0));

Пр - приемная позиция (расположена в точке с координатами (0;0;0));

b - расстояние от передающей позиции до приемной позиции (база системы);

Ц - движущаяся цель;

x, y, z - координаты цели в декартовой системе координат;

- вектор, начало которого расположено в точке расположения приемной позиции (b;0;0), а конец - в точке расположения цели (x,y,z);

- вектор, начало которого расположено в точке расположения передающей позиции (0;0;0), а конец - в точке расположения цели (x,y,z);

АВ - траектория цели;

CD - проекция траектории на горизонтальную плоскость;

- вектор скорости цели, где V_x, V_y, V_z - проекции вектора скорости на оси x, y, z;

φ - угол наклона траектории в горизонтальной плоскости по отношению к линии базы системы;

ψ - угол наклона траектории в вертикальной плоскости;

- бистатический угол (угол между векторами и );

х_П - точка пересечения целью линии базы.

На фиг.4, а, б приведена геометрическая иллюстрация процедуры поворота системы координат xyz и возможная движущаяся цель. На фиг.4, а, б обозначено:

x, y, z - исходная система координат, ось x направлена из точки расположения приемной позиции на передающую;

x, y′, z′ - декартова система координат, повернутая на угол θ вокруг оси x;

- радиус-вектор цели;

- проекция радиус-вектора на плоскость (y, z);

- вектор скорости цели;

- проекция вектора скорости на плоскость (х, y);

φ - угол наклона траектории в плоскости (х, y);

Ψ - угол наклона траектории в плоскости (y, z);

α и β - азимут и угол места цели в исходной системе координат;

γ - угол между радиус-вектором цели и осью x (остается неизменным при повороте системы координат вокруг оси x);

ξ - угол между проекцией радиус-вектора цели на плоскость (y, z) и осью z,

ξ′ - угол между проекцией радиус-вектора цели на плоскость (y, z) и осью z′ повернутой системы координат.

Римскими цифрами показаны номера квадрантов системы координат (y, z). Круговой стрелкой показано положительное направление отсчета углов.

На фиг.5 приведена блок-схема алгоритма вычисления угла поворота системы координат θ и пересчета азимута α и угла места β цели в повернутую систему координат. Практически для обеспечения приемлемой точности оценки начального приближения достаточно выполнить N=5…10 итераций.

На фиг.6 приведены графики, иллюстрирующие результаты моделирования работы предлагаемого устройства. При этом считается, что передающая позиция расположена в точке с координатами (b;0;0), а приемная - в точке с координатами (0;0;0), длина линии базы b=40 км. На фиг.6 отдельно показаны две траектории цели (I и II) для двух различных углов наклона к горизонтальной плоскости, при этом для каждого случая приведены истинная траектория движения цели (позиция 1) и траектория, полученная по измеренным значениям α, β, f_∂ и вычисленным в устройстве траекторным параметрам (позиция 2).

На фиг.7 изображены зависимости ошибок определения координаты x от значения ординаты у цели, рассчитанные для траектории движения I (фиг.6) с параметрами: х_П=15 км; φ=60°; ψ=30°; h=1 км (на момент пролета над базой); V=100 м/с. Сплошной линией (позиция 1) изображен график зависимости среднеквадратического отклонения (СКО) ошибок измерения координаты x, соответствующего потенциально достижимой точности. Пунктирной линией изображены суммарные ошибки измерения координаты x , где m_x - смещение оценки координаты, σ_х - СКО оценки координаты, полученные по результатам моделирования работы заявляемого устройства для 1000 независимых реализаций входных данных и тех же параметров системы и траектории, что и первый график (позиция 2).

На фиг.8 изображены зависимости ошибок определения координаты x в зависимости от значения ординаты у цели, рассчитанные для траектории движения II (фиг.6) с параметрами: х_П=30 км; φ=60°; ψ=-60°; h=1 км (на момент пролета над базой); V=100 м/с. Сплошной линией (позиция 1) изображен график зависимости СКО ошибок измерения координаты x, соответствующего потенциально достижимой точности. Пунктирной линией изображены суммарные ошибки измерения координаты x , полученные по результатам моделирования работы заявляемого устройства для 1000 независимых реализаций входных данных и тех же параметров системы и траектории, что и первый график (позиция 2).

Предлагаемое устройство с определением направления прихода отраженного от цели сигнала моноимпульсным методом с двумя пространственными каналами (фиг.1) состоит из передающей позиции 1 и, в удаленной от источника излучения точке, приемной позиции. Приемная позиция, в свою очередь, состоит из двух антенн, формирующих лучи соответственно в азимутальной плоскости (2) и угломестной плоскости (2′), каждая имеет два выхода, каждый из которых соединен с входом последовательного соединения приемника (3 и 3′), детектора (4 и 4′) и ФНЧ (5 и 5′). Приемник, детектор и ФНЧ каждого угломерного канала образуют вместе приемное устройство соответствующего угломерного канала. Выходы ФНЧ 5 соединены с соответствующими входами блока 6 измерения направления прихода отраженного от цели сигнала в азимутальной плоскости и блока 7 измерения доплеровской частоты. Выходы ФНЧ 5′ соединены с соответствующими входами блока 6′ измерения направления прихода отраженного от цели сигнала в угломестной плоскости. Выходы блоков измерения направления прихода отраженного от цели сигнала в азимутальной и угломестной плоскости соответственно 6 и 6′, последовательно соединены с блоком 14 пересчета измерений азимута и угла места цели для повернутой системы координат и блоком 7 измерения доплеровской частоты. Выход блока 7 измерения доплеровской частоты соединен последовательно с блоком 8 экстраполяции измеряемых параметров, блоком 9 вычисления момента времени пересечения целью линии базы, блоком 10 определения поверхности положения, блоком 11 вычисления начального приближения траекторных параметров, блоком 15 пересчета траекторных параметров из повернутой системы координат в исходную систему координат и блоком 13 вычисления траекторных параметров. Входы блока 13 вычисления траекторных параметров соединены с выходом блока 6, выходом блока 6′, выходом блока 7 и выходом блока 12 определения статистических характеристик ошибок измерения доплеровской частоты и направления прихода отраженного от цели сигнала, входы которого, в свою очередь, соединены с выходами блоков 6 и 6′ измерения направления прихода отраженного от цели сигнала в азимутальной и угломестной плоскости соответственно и выходом блока 7 измерения доплеровской частоты. При этом выход блока 14 пересчета измерений азимута и угла места цели для повернутой системы координат соединен с входом блока 8 экстраполяции измеряемых параметров и входом блока 11 вычисления начального приближения траекторных параметров, а выход блока 8 экстраполяции измеряемых параметров соединен со входом блока 10 определения поверхности положения. Выход блока 13 вычисления траекторных параметров является выходом всего устройства.

Предложенное устройство работает следующим образом. Допустим, что зондирующий сигнал непрерывный, а каждая приемная антенна (2 и 2′) имеет парциальные каналы соответственно в азимутальной плоскости (2.1 и 2.2) и угломестной плоскости (2′.1 и 2′.2) (фиг.1). При этих условиях в устройстве обеспечивается возможность измерения трех параметров сигнала, отраженного от цели: доплеровской частоты по частоте сигнала биений, образуемых при сложении отраженного от цели сигнала и прямого сигнала передатчика (эта операция осуществляется в блоке 7 измерения доплеровской частоты), угловых координат цели в азимутальной и угломестной плоскости путем сравнения амплитуд низкочастотных сигналов биений с одинаковой частотой Доплера в соответствующих парциальных каналах (блоки 6 и 6′ измерения направления прихода отраженного от цели сигнала в азимутальной и угломестной плоскости соответственно).

Рассмотрим возможность определения по измеренным значениям частоты Доплера f_∂(t) и угловых координат цели α(t) и β(t) параметров траектории движения цели в заявляемом устройстве.

Условно работу всего устройства можно разделить на два этапа. На первом из них происходит предварительная оценка местоположения цели (осуществляется в блоках 1-11, 14 и 15), а на втором - уточнение ее в соответствии с критерием максимального правдоподобия (осуществляется в блоках 12-13).

Поясним основные моменты нахождения начальной оценки траекторных параметров цели в блоках 1-11, 14-15. Измерения первичных параметров - доплеровской частоты f_∂ и угловых координат α и β - производятся в дискретные моменты времени через равные интервалы Т, и имеется n последовательных измерений этих параметров, произведенных в блоке 7 измерения доплеровской частоты и блоках 6 и 6′ измерения направления прихода отраженного от цели сигнала в азимутальной и угломестной плоскости соответственно. Для удобства эти первичные измерения можно представить в виде вектора

где

[.]^T - знак транспонирования;

^∧ - означает оценку измеряемой величины;

, , - оценки соответственно частоты Доплера, азимута и угла места цели в момент наблюдения t_n=nT, соответствующий n-ному интервалу первичных измерений ((n-1)T, nT).

Для получения начального приближения траекторных параметров следует использовать экстраполяционный алгоритм с предварительной оценкой суммарной дальности. Для получения начального приближения траекторных параметров в повернутой системе координат необходимо предварительно пересчитать в новую систему координат угловые координаты цели (α и β). Угол поворота системы координат, обеспечивающий "горизонтальный" пролет цели в новой системе координат (параллельно плоскости (x, y′)), можно приближенно определить из следующего условия:

где β′(t) - угол места цели, пересчитанный в повернутую систему координат.

Процедура поворота системы координат иллюстрируется фиг.4, б. На практике необходимый угол поворота системы координат можно найти, например, методом деления пополам (фиг.5). При этом задаются начальные значения угла поворота θ и шага его изменения Δθ и осуществляется линейная аппроксимация временной зависимости β(t) для исходной системы координат β(t)≈a_βt+b_β, где a_β, b_β - коэффициенты аппроксимации.

На каждой итерации вектор измерений угла места пересчитывается в новую систему координат, проводится линейная аппроксимация пересчитанных измерений , определяется направление поворота, изменяется угол поворота на величину шага с учетом направления и проводится замена коэффициента аппроксимации . Практически для обеспечения приемлемой точности оценки начального приближения достаточно выполнить N=5…10 итераций.

Угол ξ между проекцией радиус-вектора цели на плоскость (y, z) и осью z находится из следующего выражения:

После поворота системы координат вокруг оси x угол между проекцией радиус-вектора цели на плоскость (y, z) и осью z′ повернутой системы координат равен

Угол γ между радиус-вектором цели и осью х не изменяется при повороте системы координат. После выполнения поворота нужно пересчитать измерения азимута и угла места в повернутую систему координат:

В формулах (3)-(5) углы ξ, ξ′ приведены к интервалу [0, π/2]. Поэтому после пересчета азимута и угла места цели в повернутую систему координат следует учесть, в каком квадранте системы (y′, z′) окажется после поворота системы координат вектор и при необходимости изменить знаки рассчитанных углов.

Как известно [Теоретические основы радиолокации / под ред. Я.Д.Ширмана. М.: Сов. Радио, 1970. С.326; Справочник по радиолокации: В 4 т. / под ред. М.Сколника; пер. с англ. под. общ. ред. К.Н.Трофимова. М.: Сов. Радио, 1978. Т.4. С.199], существует следующая зависимость частоты Доплера от траектории цели:

где

λ - длина волны излучения;

r₁(t) и r₂(t) - зависимости модулей векторов и движущейся цели от времени (фиг.3);

L_Σ(t) - суммарное расстояние передатчик - цель - приемник.

Интегрирование (6) при известной соответствующей постоянной (постоянная интегрирования, равная значению суммарной дальности на момент времени t_П пролета цели над линией базы) позволяет получить зависимость L_Σ(t). Если цель движется в плоскости (x, y), то значение постоянной интегрирования на момент пересечения линии базы точно известно и равно величине базы системы (L_Σ(t_П)=b). Таким образом, до пересечения целью линии базы в блоке 8 производится экстраполяция доплеровской частоты для приближенного определения зависимости f_∂(t) от времени и определение в блоке 9 момента времени пересечения целью линии базы (для этого может также использоваться и экстраполяция угловых координат).

При движении цели на постоянной высоте необходима как экстраполяция частоты Доплера, так и азимутального и угломестного положения цели, так как в этом случае оценка момента времени пересечения линии базы может быть получена только из условия обращения в ноль азимута цели. Оценка постоянной интегрирования находится по известной длине базы системы и экстраполированному значению угла места.

Для построения с приемлемой точностью траекторий, имеющих произвольный наклон к горизонтальной плоскости, предлагается использовать следующий подход. Если повернуть оси y, z декартовой системы координат, связанной с наземной позицией, вокруг оси x, на которой расположены приемная и передающая позиции, так, чтобы плоскость траектории была параллельна плоскости (x, y′), где ось y′ получена поворотом оси y, то тем самым будет обеспечен "горизонтальный" пролет цели в новой системе координат (фиг.4, а, б). При этом оценка момента времени пересечения линии базы и постоянная интегрирования могут быть получены аналогично описанному выше случаю пролета цели на постоянной высоте.

Затем в блоке 10 на основании (6) производится оценка суммарной дальности L_∑(t) для текущего момента наблюдения. После пересечения целью линии базы оценка L_∑(t) может быть получена путем непосредственного интегрирования измеренной зависимости f_∂(t) от момента t_П до текущего момента наблюдения за целью.

По результатам измерения суммарной дальности и измерения угловой координаты начальная оценка координат цели в повернутой системе координат может быть получена как точка пересечения поверхности положения (поверхности равной суммарной дальности) и луча, проведенного из приемной позиции под измеряемыми углами прихода отраженного от цели сигнала (азимут и угол места цели), в соответствие со следующими выражениями:

Знание декартовых координат цели для двух разных моментов времени позволяет определить ее скорость движения (V_x, V_y, V_z) согласно следующей формуле:

Пересчет координат цели и их производных из исходной системы координат в повернутую систему координат (блок 15) выполняется в соответствии с правилами:

где

y, z, V_y, V_z - координаты цели и их производные в исходной системе координат;

y′, z′, - координаты и их производные в повернутой системе координат.

При этом значение координаты x и ее производной при повороте системы координат не изменяется. В формулах (8) значения углов ξ′, χ′ приведены к интервалу [0, π/2], и при вычислениях необходимо определить, в каком квадранте системы координат (y, z) (фиг.4, б) находится цель, и корректно учесть знаки координат и скоростей.

Поясним основные моменты работы устройства на втором этапе (блоки 12-13). Движение цели по линейной траектории может быть полностью описано вектором параметров:

где

x_n, y_n, z_n, V_x=V_cos(Ψ)cos(φ), V_y=Vcos(Ψ)sin(φ), V_z=Vsin(Ψ) - значения декартовых координат цели и скоростей их изменения в момент наблюдения t_n (фиг.3).

Местоположение цели в любой другой момент времени t_i можно определить по вектору параметров :

Маневрирование цели может быть учтено путем ограничения количества троек n измерений первичных параметров, используемых для оценки вектора параметров .

Задачей блоков 12-13 является наиболее точное определение вектора траекторных параметров по вектору измерений . Для этого производится уточнение предварительной оценки вектора траекторных параметров в соответствие с оптимальными критериями теории оценивания. В случае использования метода максимального правдоподобия возможно использование следующей итерационной процедуры [Черняк B.C. Многопозиционная радиолокация. М.: Радио и связь, 1993. С.369]:

где

- оценка вектора параметров на i-й итерации, i=0, 1…n;

- начальное приближение, полученное на предыдущем этапе обработки (по результатам работы блоков 1-11, 14-15);

k - параметр, определяющий скорость сходимости итерационной процедуры;

- нелинейная векторная функция, определяемая следующими зависимостями, связывающими точные значения измеряемых параметров частоты Доплера f_∂, азимута цели α и угла места β с точными значениями траекторных параметров:

- матрица размером [3n×6], каждая строка которой - градиент одной из функций , и по вектору .

R_e - корреляционная матрица ошибок первичных измерений размером [3n×3n].

На практике дискретные измерения первичных параметров производятся через интервал Т, равный или превышающий интервал корреляции оценок, поэтому матрица R_e - диагональная и содержит на главной диагонали значения , , - дисперсии ошибок измерения частоты Доплера и угловых координат, полагаемых одинаковыми для всех моментов времени i:

В случае движения цели по траекториям, близким к линейным, оценки дисперсий ошибок измерения доплеровской частоты и угловых координат , , можно получить методом линейной аппроксимации временных зависимостей первичных параметров , и (блок 12). Измерения частоты Доплера, азимута и угла места аппроксимируются линейными полиномами:

где коэффициенты аппроксимирующих полиномов a _f, b_f, а _α, b_α, а _β, b_β рассчитываются в соответствии с методом наименьших квадратов [Сейдж Э., Мэлс Дж. Теория оценивания и ее применение в связи и управлении. М.: Связь, 1976. С.238-250].

Тогда оценки дисперсий ошибок измерения первичных параметров находятся из следующих выражений:

В общем виде процесс получения оценок дисперсий ошибок измерения доплеровской частоты и угловых координат , , в результате работы блока 12 описан в изобретении «Устройство для определения параметров движения объекта», патент РФ №2154840, МПК G01S 13/06, опубликован 20.08.2000 г., авторы: Бляхман А.Б., Ковалев Ф.Н., Рындык А.Г., Сидоров С.Б.

Таким образом, в каждом из двух парциальных каналов (азимутального или угломестного угломерных каналов), состоящих из последовательного соединения приемника 3 (3′), детектора 4 (4′), ФНЧ 5 (5′), происходит выделение низкочастотного колебания (сигнала биений) путем детектирования суммарного сигнала, образуемого за счет интерференции прямого сигнала передатчика 1 и сигнала, отраженного от цели. Далее с выхода азимутального угломерного канала низкочастотное колебание поступает в блок 7 измерения доплеровской частоты и блок 6 измерения направления прихода отраженного от цели сигнала в азимутальной плоскости, а с выхода угломестного угломерного канала низкочастотное колебание поступае