Способ определения угла поворота вектора силы тяги гиперзвукового прямоточного воздушно-реактивного двигателя с косым срезом сопла по результатам летных испытаний его на гиперзвуковой летающей лаборатории

Способ определения угла поворота вектора силы тяги гиперзвукового прямоточного воздушно-реактивного двигателя с косым срезом сопла по результатам летных испытаний его на гиперзвуковой летающей лаборатории

Иллюстрации

Показать все

Реферат

Область техники.

Изобретение относится к авиадвигателестроению, а именно к новому направлению в нем - гиперзвуковым прямоточным воздушно-реактивным двигателям (ГПВРД), прежде всего - к определению угла поворота вектора силы тяги двигателя с косым срезом сопла по результатам летных испытаний ГПВРД на гиперзвуковой летающей лаборатории (ГЛЛ).

Уровень техники.

Модуль и угол поворота вектора силы тяги ГПВРД с косым срезом сопла являются важнейшими тяговыми характеристиками двигателей и летно-техническими характеристиками ГЛЛ. Серьезным препятствием, ограничивающим возможности определения тяговых характеристик таких двигателей на наземных стендах, является зависимость этих характеристик от условий обтекания ГЛЛ в натурных условиях, а также особенности интеграции двигателя с планером ГЛЛ: вся нижняя поверхность планера от носка до входа в ГПВРД профилируется как воздухозаборник, а кормовая часть от выхода из камеры сгорания до донного среза планера является соплом одностороннего расширения. Разумеется, при установке двигателя на другой планер изменяются не только аэродинамические характеристики ГЛЛ, но и тяговые характеристики ГПВРД. Воспроизведение на стенде реальных условий полета при больших скоростных напорах и высоких температурах технически трудно реализуемо, требует больших экономических затрат и в настоящее время практически невозможно.

Существенное дополнение в методику определения вектора силы тяги двигателя с косым срезом сопла вносит изменение угла поворота вектора в процессе работы двигателя; величина угла отклонения может достигать 20÷25°. Задача летных испытаний - определить как можно точнее этот угол, в особенности при его малых значениях.

В настоящее время проводятся исследования тяговых характеристик двигателей, обеспечивающих отклонение направления вектора силы тяги (И.А.Браилко, Ю.М.Клестов, С.Ю.Крашенинников, А.К.Миронов "Экспериментальное и расчетное исследование аэродинамики плоского поворотного сопла с резким изменением контура в горле". ЦИАМ им. П.И.Баранова, "Аэромеханика и газовая динамика ", №3). Проводятся исследования сопел, которые могли бы обеспечить поворот вектора силы тяги. Один из вариантов - геометрический поворот сопла, который задается системой управления и который может быть достаточно точно измерен. Для сопел с отклонением потока в сверхзвуковой части выявлена зависимость угла направления вектора силы тяги от величины перепада давления. При малых сверхзвуковых перепадах давления на сопле обнаружено существенное превышение эффективного угла направления силы тяги по сравнению с геометрическим углом поворота сверхзвуковых створок сопла. Из-за косого среза выходного сопла и взаимодействия выхлопной струи с внешним потоком, а также с нижней частью корпуса ГЛЛ, происходит отклонение струи на выходе из сопла и, соответственно, отклонение вектора силы тяги от оси oX₁. До настоящего времени решению задачи определения величины этого угла, в том числе при проведении летных испытаний летательных аппаратов, не уделено должного внимания.

Близким к указанному является результат, изложенный в патенте RU №2122963 от 10.12.1998 г. «Система управления двухдвигательного самолета посредством управления вектором тяги». В этой системе осуществляется координация сигналов на стабилизаторы в зависимости от механического поворота сопла левого и правого двигателя с целью обеспечения устойчивости в продольном и путевом каналах управления.

Известен "Стенд для определения вектора тяги двигателя с кососрезанным соплом", патент С2 №2274764 от 20 апреля 2006 г. В предложенной методике модуль вектора силы тяги определяется по показаниям силоизмерителей в направлениях двух ортогональных осей. Направление вектора силы тяги определяется путем геометрических построений фактической схемы испытаний двигателя (наложением проекции двигателя на вычисленный вектор тяги).

Существенным недостатком предложенной методики является то, что она может быть использована только при работе на стенде. Кроме того, угол поворота определяется путем сложных геометрических построений, что не позволит определить его с высокой точностью.

Известен "Метод измерения тяги реактивного двигателя в реальном масштабе времени, патент EP №0342970. А2 от 19 мая 1988 г. В данном методе полная тяга двигателя определяется как разность общей силы, включающей подъемную силу самолета и силу аэродинамического сопротивления с учетом углов атаки и скольжения. Для определения этих составляющих в алгоритме расчетов используется большое количество измеряемых параметров, в том числе и перегрузок, измеряемых с помощью акселерометров.

Существенным недостатком данного метода является большая погрешность, которая обусловлена измерением в полете большого количества параметров, в том числе термодинамических параметров смеси газа: температур, показателей изоэнтропы (k), газовой постоянной (R), с учетом реального состава газа. В этом методе ставится задача определения только модуля вектора силы тяги.

Известен “Способ измерения тяги в полете гиперзвукового прямоточного воздушно-реактивного двигателя (ГПВРД) непилотируемой гиперзвуковой летающей лаборатории (ГЛЛ)”, патент RU №2242736 от 20 декабря 2004 г.

В данном способе тяга двигателя определяется по приращению продольного ускорения (вдоль оси oX₁), создаваемого за счет действия силы тяги в полете. Для определения тяги двигателя производится разделение сил аэродинамического сопротивления вдоль продольной оси ГЛЛ, земного тяготения и тяги двигателя. С этой целью производится выключение и включение подачи топлива в камеру сгорания в короткие рядом стоящие промежутки времени t₁ и t₂, которые не превышают 1 сек. Силу тяги двигателя определяют по формуле

R_ДВ=m_лл·ω_R,

где m_лл - масса ГЛЛ,

ω_R - ускорение ГЛЛ при действии силы тяги.

Ускорение ГЛЛ вычисляют по формуле

ω_R=(n_xt1-n_xt2)·g,

где n_xt1 и n_xt2 - значения продольных перегрузок в моменты времени t₁ и t₂,

g - ускорение свободного падения.

Существенным недостатком такой системы измерений с одним акселерометром является невозможность определения угла поворота вектора силы тяги.

Наиболее близким техническим решением, принятым за прототип, является “Способ определения вектора силы тяги гиперзвукового прямоточного воздушно-реактивного двигателя (ГПВРД) с косым срезом сопла по результатам летных испытаний его на гиперзвуковой летающей лаборатории (ГЛЛ)”; патент №2314503 от 18 июля 2004 г.

Технический результат при использовании такого способа достигается за счет измерения перегрузки, создаваемой действием силы тяги двигателя в полете в строго определенном направлении, и внешнетраекторных измерений относительной скорости. При определенном повороте измерительной оси акселерометра исключается в его показаниях составляющая от действия суммарных аэродинамических сил и остается составляющая только от силы тяги.

При этом дается формула для вычисления угла поворота измерительной оси (оси чувствительности) в зависимости от аэродинамических характеристик ГЛЛ; используются заданные аэродинамические характеристики ГЛЛ, принятые за номинальные. Формула получается из условия равенства нулю проекции вектора полной аэродинамической силы, включающей в себя силу лобового сопротивления Q и подъемную силу Y.

Вычисления угла поворота вектора силы тяги при малых его значениях и при наличии больших погрешностей акселерометров показали, что невозможно добиться дальнейшего повышения точности определения угла поворота на основании указанных в прототипе средств измерений. Поэтому необходимо использование других характерных параметров, которые наиболее чувствительны к изменению угла поворота вектора силы тяги, и средств измерения этих параметров. Такими параметрами могут служить моменты вращения ГЛЛ относительно центра масс при повороте вектора силы тяги и углы отклонения рулей высоты для устранения этих моментов.

Раскрытие изобретения.

Технический результат, на достижение которого направлено изобретение, заключается в повышении точности определения угла поворота вектора силы тяги гиперзвукового прямоточного воздушно-реактивного двигателя с косым срезом сопла за счет привлечения дополнительных измерений параметров в короткопериодическом движении ГЛЛ вокруг центра масс.

Указанный технический результат достигается тем, что в способе определения вектора силы тяги гиперзвукового прямоточного воздушно-реактивного двигателя с косым срезом сопла по результатам летных испытаний его на гиперзвуковой летающей лаборатории, включающем операции измерения перегрузки на ГЛЛ от действия силы тяги двигателя при условии равенства нулю в показаниях акселерометра проекции вектора полной аэродинамической силы, вычисление модуля вектора силы тяги Р_∂вt текущий момент времени, в установившемся режиме полета ГЛЛ, при котором сумма продольного аэродинамического момента и момента от силы тяги двигателя равна нулю, дополнительно задают импульсное ступенчатое отклонение руля высоты на угол δ_имп, величину которого выбирают на основании результатов предварительного математического моделирования из условия, чтобы разность Δα=α-α₀ между текущим значением угла атаки α в режиме колебаний и значением его α₀ в момент подачи импульса по модулю не превышала требуемое при проведении эксперимента значение , измеряют в возмущенном движении углы отклонений рулей высоты и вращающие моменты, при таком испытании измеренные моменты будут определять отклонение только аэродинамического момента M_Zаэр. от балансировочного M_{Zаэр.бал.}, который уравновешен моментом от тяги двигателя. Определяют отклонение момента как разность ΔM_Zаэр.=M_Zаэр.-M_{Zаэр.бал.}, вносят коррекцию в значение ΔM_Zаэр. на величину где

- производная по углу атаки от коэффициента аэродинамического момента. Определяют предварительно расчетным путем и по результатам наземных стендовых испытаний координаты l и h точки приложения вектора силы тяги на срезе сопла относительно центра масс ГЛЛ, далее вычисляют приращение аэродинамического момента, обусловленное только отклонением руля относительно его балансировочного значения при подаче импульса и равное разности:

ΔM_Z≈ΔM_Zаэр.-ΔM_Zα, где

ΔM_Zаэр. измеренное значение аэродинамического момента в возмущенном движении.

Затем по результатам измерений, полученных в летных испытаниях, вычисляют производную по углу отклонения руля высоты от коэффициента аэродинамического момента по формуле

где Δδ=δ-δ₀ - разность между измеренными значениями угла отклонения руля высоты δ в возмущенном движении и его балансировочным значением δ₀, измеренным при подаче импульса,

q - измеренное значение скоростного напора,

s,b - характерная площадь и длина изделия.

В установившемся режиме после подачи импульса измеряют текущие значения скоростного напора, угла отклонения руля высоты и находят угол поворота φ вектора силы тяги - Р_двt в результате решения тригонометрического уравнения:

где Р_двt - значение модуля вектора силы тяги в текущий момент времени t,

которое определяется по показаниям акселерометров,

δ_t, q_t - текущие значения руля высоты и скоростного напора в установившемся состоянии после подачи импульса,

l и h - координаты точки приложения вектора силы тяги на срезе сопла.

Таким образом достигается технический результат, на достижение которого направлено изобретение: повысить точность определения угла поворота вектора силы тяги ГПВРД с косым срезом сопла.

Изобретение поясняется чертежами, на которых:

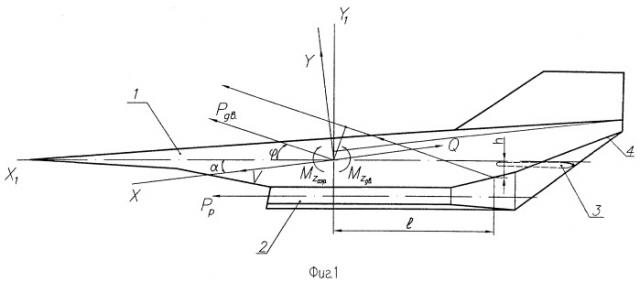
на фиг.1 показана схема распределения сил и моментов относительно центра масс ГЛЛ:

1 - ГЛЛ,

2 - экспериментальный ГПВРД,

3 - руль высоты,

4 - срез сопла;

oX₁Y₁ - связанная система координат,

oXY - скоростная система координат, ось оХ повернута на угол атаки α относительно оси oX₁, по осям оХ и oY направлены сила лобового сопротивления Q и подъемная сила Y, по оси оХ направлен вектор относительной скорости V;

Р_дв - тяга двигателя, приведенная к центру масс,

Р_р - реактивная сила тяги двигателя;

φ - угол поворота вектора силы тяги;

M_аэр., M_дв - моменты вращения относительно центра масс от действия аэродинамических сил и силы тяги двигателя;

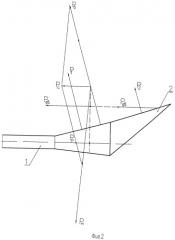
на фиг.2 показано распределение сил тяги двигателя на срезе сопла:

1 - тракт двигателя,

2 - сопло двигателя,

P₁/P₂ - тяги двигателя на верхнем внутреннем и внешнем срезах сопла;

Р_B - суммарная тяга двигателя на верхнем срезе сопла (геометрическая сумма векторов сил P₁ и Р₂,);

P_H - тяга двигателя на нижнем срезе сопла,

P_C - суммарная тяга двигателя на срезе сопла (геометрическая сумма векторов сил Р_B и Р_H в точке их пересечения),

Р_р - реактивная сила тяги;

Р_дв - суммарная тяга двигателя, приведенная к срезу сопла (геометрическая сумма векторов сил Р_Р и Р_С);

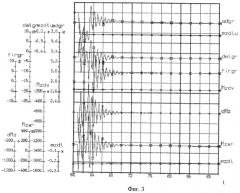
на фиг.3 представлены в качестве примера результаты математического моделирования; показано изменение по времени параметров и характеристик в короткопериодическом движении ГЛЛ вокруг центра масс; задано ступенчатое отклонение руля высоты на угол Δδ=5° при t=60 сек, отклонение вектора силы тяги - на угол φ=5°.

М_zаэр. и М_zдв. (Mzar и Mzdv) - моменты от аэродинамических сил и от силы тяги двигателя,

ΔM_z, (dMz) - сумма этих моментов,

- частная производная коэффициента момента тангажа (заданная - mzdl, вычисленная по результатам измерений (результаты математического моделирования - mzdlu),

δ (delgr, в градусах) - угол отклонения руля высоты относительно балансировочного значения,

α (adgr) - угол атаки,

φ (firgr) - угол отклонения вектора силы тяги.

Предлагаемый способ определения вектора силы тяги гиперзвукового прямоточного воздушно-реактивного двигателя (ГПВРД) (2) с косым срезом сопла по результатам летных испытаний его на гиперзвуковой летающей лаборатории (ГЛЛ) (1) осуществляют в следующей последовательности:

устанавливают по осям вращения рулей высоты датчики моментов и углов отклонения рулей;

устанавливают датчики давления (скоростного напора);

замеряют по осям oX₁ и oY₁ координаты l и h от центра масс ГЛЛ до расчетной точки приложения силы тяги на срезе сопла;

по результатам моделирования выбирают ориентировочно время подачи импульсного ступенчатого возмущения на руль высоты;

в процессе полета задают импульсное ступенчатое возмущение на руль высоты;

замеряют величины моментов, углов отклонений рулей высоты, скоростного напора;

вносят коррекцию с учетом заданной частной производной в измеренное значение аэродинамического момента при отклонении угла атаки от заданного номинального;

вычисляют значение частной производной ;

вычисляют значение угла поворота вектора силы тяги двигателя в результате решения тригонометрического уравнения:

Результаты вычислений угла представлены на фиг.3.

Принцип разделения в показаниях акселерометров проекций перегрузки от аэродинамических сил и силы тяги двигателя и средства измерения (акселерометры и внешнетраекторные измерения), используемые в представленном в прототипе способе определения угла поворота, не позволяют добиться дальнейшего существенного повышения точности определения угла поворота вектора силы тяги. Поэтому ставится задача использования других измеряемых параметров, которые более чувствительны к изменению угла поворота вектора силы тяги. Такими параметрами могут быть моменты вращения вокруг центра масс летательного аппарата и соответствующие им углы отклонения рулей высоты.

Динамика пространственного движения ЛА определяется двумя основными законами: изменениями количества движения и момента количества движения. Первый из них характеризует длиннопериодическое движение центра масс под действием равнодействующей, проходящей через центр масс ЛА, всех внешних сил, второй - короткопериодическое вращательное движение вокруг центра масс под действием главного момента относительно центра масс всех внешних сил.

Пространственная система сил, главный вектор которой не равен нулю и не перпендикулярен к главному моменту, может быть приведена к динаме - совокупности силы и пары, плоскость которой перпендикулярна к линии действия силы. Вектор силы можно переносить вдоль линии действия силы. Рассматриваются силы в продольной плоскости. Центр приведения целесообразно выбрать в центре масс ЛА, в соответствии с принятым распределением сил: аэродинамические силы можно привести к одной результирующей - полной аэродинамической силе, и результирующему моменту - полному аэродинамическому моменту, действующему относительно центра масс ЛА. При повороте вектора силы тяги система сил может быть приведена к этой же указанной системе. Дополнительно возникающий момент при отклонении вектора силы на угол φ должен быть скомпенсирован аэродинамическим моментом за счет отклонения руля высоты для выполнения условия балансировки на заданном угле атаки: М_дв=М_аэр.

Указанная система сил и моментов положена в основу алгоритма определения угла поворота вектора силы тяги ГПВРД, см. фиг.1.

Основная суть проблемы состоит в том, что при этом необходимо найти способ разделения в показаниях датчика момента составляющих, зависящих от аэродинамических сил и от поворота силы тяги двигателя.

Этот результат достигается за счет, прежде всего, того, что в установившемся режиме полета ГЛЛ сумма продольного аэродинамического момента и момента от силы тяги двигателя равна нулю. При отклонении руля высоты от этого равновесного балансировочного значения возникает момент, который при таком испытании будет содержать только аэродинамическую составляющую момента. По измеренным значениям момента и углам отклонения рулей можно вычислить коэффициент аэродинамического момента и далее - полный аэродинамический момент, который в установившемся режиме был уравновешен моментом от двигателя.

Как видно из фиг.1, в случае выбора точки приведения сил в центре масс при отсутствии поворота вектора силы тяги создается момент (на фиг.1 - кабрирующий), который уравновешивается аэродинамическим моментом при номинальном балансировочном значении руля высоты. При отклонении вектора силы тяги вверх от нулевого положения будет создаваться пикирующий момент.

Система уравнений углового движения имеет вид:

,где

- момент от аэродинамических сил;

- приведенный момент от аэродинамических сил;

- приведенный момент от силы тяги двигателя;

ω_x, ω_y, ω_z - угловые скорости вращения ГЛЛ относительно связанных осей;

I_x, I_y, I_z - моменты инерции ГЛЛ относительно связанных осей;

υ - угол тангажа;

- производные коэффициента аэродинамического момента соответственно по углу атаки, углу отклонения руля и по угловой скорости;

принято b=4.39 м², I_z=1400 кг м².

Уравнение момента от аэродинамических сил может быть представлено в виде:

где

α_δ - балансировочное значение угла атаки.

Из этой формулы следует, что в установившемся режиме при α=α_δ приращение аэродинамического момента будет соответствовать такому отклонению руля относительно балансировочного значения, которое уравновесит момент от силы тяги двигателя, обусловленный поворотом вектора силы тяги относительно расчетного номинального значения. В величине момента от тяги двигателя рассматривается составляющая момента, обусловленная поворотом вектора силы тяги, и составляющая момента ΔM_zдв.=-P_дв.h, равная величине кабрирующего момента при отсутствии поворота вектора силы тяги. Направление при отсутствии поворота вектора принимается за номинальное расчетное. Оно может не совпадать с продольной осью двигателя и будет зависеть от распределения сил на срезе сопла. В общем случае все силы могут быть приведены к динаме в центре масс ГЛЛ. Схема распределения сил на косом срезе сопла показана на фиг.2.

На этом рисунке показаны расчетные значения сил при числе М=7 и угле атаки α=4° для одного из вариантов тяговых характеристик;

здесь Р_Н и Р_В - суммарные силы на нижней и верхней поверхностях сопла,

Р_Р - реактивная сила.

В результате геометрического сложения указанных сил P_Н и P_В получим суммарное значение силы на срезе сопла - Р_С, и суммарное значение силы тяги P_дв. - в результате сложения сил Р_С и Р_Р. Вдоль линии действия суммарная сила тяги приведена к срезу сопла. Через полученную точку в направлении, параллельном оси ox₁, проходит вектор силы тяги при нулевом угле поворота. Составляющая момента ΔМ_zдв.=-Р_дв.h, обусловленная расположением двигателя с косым срезом сопла под фюзеляжем, ниже строительной оси ox₁, при отсутствии поворота вектора силы тяги уравновешивается аэродинамическим моментом при расчетном балансировочном положении руля высоты, т.е. при отсутствии поворота вектора силы тяги сумма момента аэродинамических сил и указанного кабрирующего момента от силы тяги двигателя будет равна нулю. В установившемся режиме дополнительное отклонение руля высоты от указанного балансировочного значения будет зависеть практически только от угла поворота вектора силы тяги.

В соответствии с фиг.1 и принятыми условиями, формула для вычисления момента М_zдв., создаваемого силой тяги двигателя на плече l относительно центра масс, имеет вид:

Для одной из рассмотренных компоновок ГЛЛ получено: l=1.561 м, h=0.24 м. При повороте вектора силы тяги равновесие моментов в условиях балансировки будет выполняться уже при другом значении руля высоты. Отличие этого значения от балансировочного будет характеризовать поворот вектора силы тяги. Так как при малых углах поворота изменение проекции на ось ox₁ незначительно, то момент силы будет зависеть главным образом от величины проекции силы на ось оy₁.

Указанная форма записи уравнений моментов позволяет проводить вычисление аэродинамического момента М_zаэр. при отклонении руля высоты относительно нулевого значения. Таким образом решается задача определения угла поворота вектора силы тяги в линейном приближении. Относительно указанной исходной схемы рассматриваются далее моменты при повороте вектора силы тяги. Такой подход к решению задачи правомерен и позволяет упростить ее решение, прежде всего при малых углах φ.

Возможность повышения точности определения углов поворота в малом диапазоне значений позволит скомпенсировать недостатки алгоритма, изложенного в прототипе. Предполагается, что модуль вектора силы тяги определяется по показаниям акселерометра в текущий момент времени во всем диапазоне возможных значений угла φ.

В дополнение к сказанному, при составлении алгоритма определения угла поворота φ принимаются во внимание большой скоростной напор, соотношения между коэффициентами аэродинамических моментов и требования к работе системы стабилизации углов атаки и скольжения: обеспечить полет практически при постоянных углах атаки и скольжения, т.е. при малых значениях угловых скоростей ω_x, ω_y, ω_z.

При больших скоростных напорах q и малых значениях угловых скоростей ω_x, ω_y, ω_z можно пренебречь произведением ω_x·ω_y и, следовательно, моментом от инерционных сил. Кроме того, принято Тогда второе из уравнений (3) можно представить в виде:

.

На фиг.3 показаны изменения параметров и характеристик в короткопериодическом движении ГЛЛ вокруг центра масс; задано ступенчатое отклонение руля высоты на угол Δδ=5° при t=60 сек; отклонение вектора силы тяги - на угол φ=5°. При этом сохраняется режим непрерывной стабилизации угла атаки. Такой режим полета с незначительным возмущением практически не нарушает требуемые условия сохранения значений угла атаки и скоростного напора, т.е. требуемых условий на входе в воздухозаборник. В то же время он позволяет получить дополнительную информацию о влиянии высокочастотных колебаний угла атаки на величину силы тяги. Такая информация может быть получена на основании показаний акселерометров при определенной ориентации измерительных осей; обоснование такой возможности было дано в прототипе.

Как видно из фиг.3, при номинальных условиях в установившемся режиме при t>72 сек. вычисленное значение угла φ≈5°(4.85°…5.15°), т.е. близкое к заданному на значительном интервале времени (Δt≈20 сек).

При непрерывном измерении моментов и углов отклонений рулей вычисленное значение может быть использовано при послеполетной обработке в широком промежутке времени как до подачи импульса, так и в установившемся режиме после возмущения. Это позволит определять угол поворота вектора силы тяги на достаточно продолжительном интервале времени.

Для решения задачи в более широком временном диапазоне также может быть использован дополнительно колебательный режим на начальном участке с момента включения двигателя. Поэтому целесообразно осуществлять запуск ГПВРД с запаздыванием в несколько сек после отделения от ускорителя, с момента установления требуемого балансировочного угла атаки. Аналогично, после окончания работы двигателя, поддерживать стабилизацию заданных значений скоростного напора и угла атаки.

Как видно из фиг.3, в установившемся режиме ΔM_z≈0. В переходном процессе при постоянном значении силы тяги получим ΔM_z≈ΔM_zаэр.; отклонения угла атаки от номинального по модулю не превышают 0.3°. При малых отклонениях угла атаки от номинального значения приращение момента можно представить в виде:

, где

Δδ=δ_t-δ_to - разность между текущим значением руля и значением его перед подачей импульса.

Момент может быть достаточно точно измерен с помощью датчика момента (в частности, ДМ-18, ДМ-20, ВТ-191); погрешность измерений моментов ≈1%.

При необходимости, в случае больших колебаний, можно внести коррекцию на величину момента , используя расчетные значения моментных характеристик и измеренные значения скоростного напора, угла атаки и угловой скорости. При ω_z≈0 правомерно ранее указанное принятое условие =0 и можно пренебречь составляющей момента демпфирования, в сравнении со статической составляющей от поворота руля высоты и отклонения угла атаки от расчетного балансировочного.

В итоге, получим равновесие моментов - аэродинамического, только от величины угла отклонения руля относительно балансировочного значения, и от силы тяги двигателя при повороте вектора силы на угол φ. С целью повышения точности вычислений при обработке результатов измерений следует принимать для расчетов значения измеряемых параметров в моменты максимальных отклонений руля в режиме колебаний после подачи возмущений.

Следовательно, по измеренным в летном эксперименте величинам ΔM_z, δ, q можно вычислить частную производную коэффициента продольного момента по углу отклонения руля высоты следующим образом:

Отметим, что здесь величина Δδ - отклонение руля высоты относительно балансировочного значения, измеренного в момент подачи импульса. Тогда в установившемся режиме приращение момента за счет отклонения вектора силы тяги должно быть уравновешено приращением аэродинамического момента, который может быть вычислен с использованием указанной формулы. При условии медленного изменения производной на достаточно продолжительном участке полета можно принять ≈const и использовать полученные соотношения на всем этом участке полета.

Возможно смещение точки приложения силы тяги относительно расчетной точки на срезе сопла, т.е. отступление от принятой схемы распределения сил. Тогда изменится кабрирующий момент на величину P_двt·Δh и, в соответствии с этим, - балансировочное значение руля высоты, относительно которого вычисляется приращение Δδ. Изменение плеча l, влияющее на величину угла φ, изменится незначительно. В частности, при срезе сопла в 45° изменение плеча l не превысит 2%. Следовательно, принятая система распределения сил остается справедливой при смещении точки приложения силы тяги в достаточно широком диапазоне.

Результаты статистического моделирования измерительной системы подтверждают работоспособность ее при действии случайных возмущений. Ошибки определения угла поворота вектора силы тяги при заданных случайных возмущениях характеризуются следующими параметрами: среднее квадратическое отклонение не превышает σ_φ=0.2° при математическом ожидании m_φ=0.2°.

Следовательно, при использовании представленного способа удается существенно повысить точность определения угла поворота вектора силы тяги. Это, прежде всего, является следствием того, что поворот вектора силы даже на малый угол сказывается в первую очередь на величине момента. Изменение модуля вектора силы тяги при этом незначительно. При увеличении расстояния от центра масс ЛА до среза сопла (плеча силы) величина момента и, следовательно, точность вычисления угла увеличится. Для уточнения полученных значений модуля и угла поворота вектора силы тяги следует произвести послеполетное математическое моделирование траекторий полета с привлечением полученных результатов обработки бортовой системы измерений и результатов внешнетраекторных измерений.

Заявляемое решение дает возможность определить в летном эксперименте угол поворота и уточнить значение модуля вектора силы тяги (из прототипа). Такой способ может быть использован при испытании всех двигателей, в особенности двигателей, в которых выявлена зависимость угла направления вектора силы тяги от величины перепада давления в тракте двигателя.

Предложенный способ может быть использован для определения вектора силы тяги по результатам измерений моментов в короткопериодическом движении, углов отклонений рулей высоты и скоростного напора при осуществлении полетов летательных аппаратов с прямоточными реактивными двигателями.

При более точном определении угла поворота вектора силы тяги могут быть уточнены характеристики потока газов из сопла, запасы управляемости ГЛЛ в продольном движении, что позволит повысить точность стабилизации угла атаки и в конечном итоге - выдать рекомендации при разработке двигателя.

Способ определения угла поворота вектора силы тяги гиперзвукового прямоточного воздушно-реактивного двигателя с косым срезом сопла по результатам летных испытаний его на гиперзвуковой летающей лаборатории, включающий операции измерения перегрузки на ГЛЛ от действия силы тяги двигателя при условии равенства нулю в показаниях акселерометра проекции вектора полной аэродинамической силы, вычисление модуля вектора силы тяги Р_двt в текущий момент времени, отличающийся тем, что в установившемся режиме полета ГЛЛ, при котором сумма продольного аэродинамического момента и момента от силы тяги двигателя равна нулю, дополнительно задают импульсное ступенчатое отклонение руля высоты на угол δ_имп, величину которого выбирают на основании результатов предварительного математического моделирования из условия, чтобы разность Δα=α-α₀ между текущим значением угла атаки α в режиме колебаний и значением его α₀ в момент подачи импульса по модулю не превышала требуемое при проведении эксперимента значение |Δα|<0.5°, измеряют в возмущенном движении углы отклонений рулей высоты и вращающие моменты, при таком испытании измеренные моменты будут определять отклонение только аэродинамического момента М_Zаэр от балансировочного М_{Zаэр.бал}, который уравновешен моментом от тяги двигателя, определяют отклонение момента как разность ΔM_Zaэp=M_Zaэp-M_Zaэp.бaл, вносят коррекцию в значение ΔМ_Zаэр на величину , где - производная по углу атаки от коэффициента аэродинамического момента; определяют предварительно расчетным путем и по результатам наземных стендовых испытаний координаты l и h точки приложения вектора силы тяги на срезе сопла относительно центра масс ГЛЛ, далее вычисляют приращение аэродинамического момента, обусловленное только отклонением руля относительно его балансировочного значения при подаче импульса и равное разности:ΔM_Z≈ΔM_Zаэр-ΔM_Zα, гдеΔM_Zаэр - измеренное значение аэродинамического момента в возмущенном движении, затем по результатам измерений, полученных в летных испытаниях, вычисляют производную по углу отклонения руля высоты от коэффициента аэродинамического момента по формуле: Δδ=δ-δ₀ - разность между измеренными значениями угла отклонения руля высоты δ в возмущенном движении и его балансировочным значением δ₀, измеренным при подаче импульса,q - измеренное значение скоростного напора,s, b - характерная площадь и длина изделия,в установившемся режиме после подачи импульса измеряют текущие значения скоростного напора, угла отклонения руля высоты и находят угол поворота φ вектора силы тяги Р_двt в результате решения тригонометрического уравнения: Р_двt - значение модуля вектора силы тяги в текущий момент времени t, которое определяется по показаниям акселерометров,δ_t, q_t - текущие значения руля высоты и скоростного напора в установившемся состоянии после подачи импульса,l и h - координаты точки приложения вектора силы тяги на срезе сопла.