Устройство для определения функций ценности единичных оценочных показателей сложных технических систем
Иллюстрации
Показать всеИзобретение относится к вычислительной технике и может быть использовано для определения функций ценности единичных показателей, которые характеризуют их влияние на качество сложных технических систем (СТС). Техническим результатом является повышение достоверности оценки технического уровня СТС, за счет выявления предпочтения единичного числового показателя. Устройство содержит группу входных регистров, три входных регистра, группу коммутаторов, блок возведения в степень, элемент задержки, два блока вычитания, коммутатор, два блока умножения, квадратор, три группы сумматоров с накоплением, группу блоков вычитания, две группы блоков деления, три группы элементов задержки, группу регистров, две группы ключей, группу квадраторов, элемент ИЛИ, блок сравнения, блок деления, две группы блоков индикации, генератор тактовых импульсов и распределитель импульсов. 11 ил., 32 табл.
Реферат
Изобретение относится к вычислительной технике и может быть использовано для определения функций ценности единичных показателей, которые характеризуют их влияние на качество сложных технических систем (СТС).
Заявителям неизвестно, чтобы такая техническая задача решалась. Это объясняется тем, что в конкретных практических задачах этим фактором часто пренебрегают.
Техническим результатом заявленного решения является выявление предпочтения единичного числового показателя на шкале от нуля до единицы для повышения достоверности оценки технического уровня СТС. Это дает возможность производить оценку степени влияния данного и других единичных показателей на выполнение основных функций СТС в нормированном виде (т.е. независимо от размерности оценочного показателя) при определении технического уровня СТС.
Кроме того, появляется возможность определить граничные значения оценочных единичных показателей, т.е. диапазоны допустимых изменений значений показателей. Под единичным показателем следует понимать параметр или характеристику, которые определяют основные свойства СТС и существенным образом влияют на ее функционирование.
Таким образом, формируется функция, участвующая в определении технического уровня СТС.
Определение функций ценности единичных показателей СТС осуществляется в следующем порядке:
1. Определение перечня единичных показателей.
2. Определение типа функции ценности для каждого единичного показателя.
3. Установление граничных значений единичных показателей.
4. Подбор функции ценности каждым экспертом.
5. Проверка степени согласованности экспертных оценок.
Исходной информацией для этих процедур является матрица опроса к-го эксперта, представленная в таблице 1 (этапы с 1-го по 4-й).
| Таблица 1 | |||||
| Матрица опроса к-го эксперта | |||||
| Показатели | Значения показателя | ||||
| Uiк1(gi)=0,10 | Uiк2(gi)=0,20 | Uiк3(gi)=0,50 | Uiк4(gi)=0,70 | Uiк5(gi)=0,90 | |
| g1 | |||||
| gi | |||||
| gn |
Количество этих таблиц определяется числом экспертов, участвующих в опросе.
В таблице 1 приняты следующие обозначения:
Uiкк(gi) - функция ценности, которая устанавливает соответствие между значениями показателя и шкалой от 0 до 1.
gi - единичный показатель, влияющий на качество СТС.
Функция ценности устанавливает приоритеты между различными значениями единичного показателя. Для каждого типа показателя в принципе может назначаться свой вид функции ценности.
Функция ценности для логических показателей является бинарной и принимает значения 0 или 1 в зависимости от того желательно данное свойство или нет. В дальнейшем будем рассматривать числовые показатели, которые предусматривают введение пяти точек.
Числовые значения в каждой строке таблицы 1 определяют характер изменения функции ценности: она может быть монотонно убывающей или возрастающей, линейной, выпуклой или вогнутой, S-образной, треугольной и трапецеидальной формы и т.д.
Целесообразно получить осредненные показатели gij для каждой j-й точки по следующей зависимости по всем экспертам:
где giкj - значение показателя из таблицы 1;
j=1, …, 5; к=1, …, m; i=1, …, n;
m - число экспертов, участвующих в опросе;
n - количество единичных показателей.
Эти осредненные показатели можно представить в виде таблицы 2.
| Таблица 2 | |||||
| Матрица осредненных показателей | |||||
| Показатели | Значения показателя | ||||
| Ui1(gi)=0,10 | Ui2(gi)=0,20 | Ui3(gi)=0,50 | Ui4(gi)=0,70 | Ui5(gi)=0,90 | |
| g1 | |||||
| gi | |||||
| gn |
Числовые значения в каждой строке таблицы 2 определяют внешний вид искомой функции ценности.
Однако возникает необходимость проверки степени согласованности экспертных оценок (этап 5-й). Это можно осуществить с помощью коэффициента конкордации Wj, который оценивается для каждой из пяти точек функции ценности по следующей формуле:
i=1, …, n; к=1, …, m; j=1, …, 5;
где dijк - нормированное отклонение текущего значения показателя giкj от его средней величины, определяемой по формуле (1).
Величина dijк оценивается по следующей формуле:
Если соблюдается неравенство
где W∂ - допустимое значение коэффициента конкордации, то результаты опроса экспертов можно признать согласованными.
В противном случае необходимо скорректировать результаты опроса экспертов путем его повторного проведения.
Для иллюстрации рассмотрим конкретный пример. Определим функции ценности единичных показателей грузового автомобиля. Выделим шесть его функциональных единичных показателей:
1) скорость (U, км/ч);
2) вместимость (V, м3);
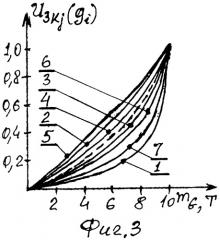
3) масса перевозимого груза (mG, т);
4) масса снаряженного автомобиля (ma, т);
5) угол разворота (α, град);
6) мощность двигателя (P, л.с).
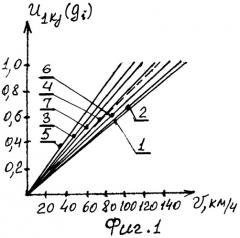
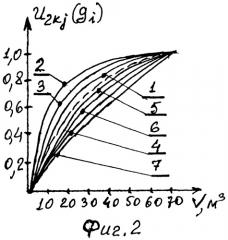
На фиг. с 1 по 6 представлены функции ценности для этих показателей, причем учтены мнения каждого из семи экспертов. Номера кривых на каждой фигуре соответствуют номерам соответствующих экспертов.
Числовые значения показателей, снятые с этих кривых, представлены в табл.3-9 для каждого эксперта. Табл. 10 содержит информацию о средних значениях показателей, основанных на показаниях экспертов. В табл.11-17 приведены разности между средними величинами единичного показателя и значениями этого показателя по мнению каждого эксперта для каждой j-й точки функции ценности. Поскольку в дальнейшем будет возведение в квадрат, то знак перед этими разностями не имеет значения и поэтому в этих таблицах приведены модули разностей.
В табл.18-24 помещены нормированные значения этих разностей, полученные в соответствии с формулой (3).
В табл.25-31 приведены квадраты этих нормированных значений для каждого эксперта по всем точкам кривых функций ценности. В табл.32 помещены итоги суммирования квадратов нормированных разностей и оценки Wj по формуле (2). Из этой таблицы видно, что каждое значение Wj больше 0,99. Это свидетельствует о хорошей согласованности действий экспертов и даже при W∂=0,80 полученные средние значения функции ценности единичных показателей грузового автомобиля (табл.10) можно принять за основу. Полученные функции ценности этих показателей представлены на фиг.1-6 в виде пунктирных линий.
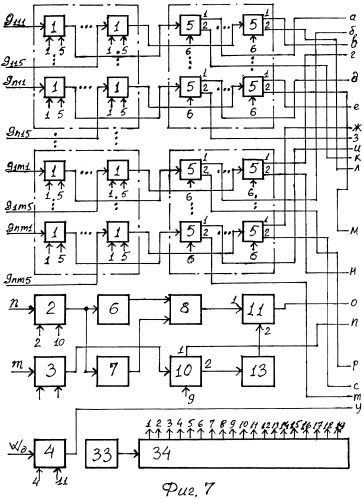
Технический результат достигается тем, что устройство для определения функций ценности единичных оценочных показателей сложных систем содержит группу входных регистров, включающую m матриц, каждая из которых состоит из 5×n элементов, первый, второй и третий входные регистры, группу коммутаторов, включающую m матриц, каждая из которых состоит из 5×n элементов, блок возведения в степень, элемент задержки (ЭЗ), первый и второй блоки вычитания, коммутатор, первый и второй блоки умножения, квадратор, первую и вторую группы сумматоров с накоплением, каждая из которых состоит из 5×n элементов, третью группу сумматоров, состоящую из пяти элементов, группу блоков вычитания, включающую m матриц, каждая из которых
| Таблица 3 | |||||
| Числовые значения показателей для эксперта №1 | |||||
| № показателя | Значения показателя | ||||
| Ui11(gi)=0,10 | Ui12(gi)=0,20 | Ui13(gi)=0,50 | Ui14(gi)=0,70 | Ui15(gi)=0,90 | |
| 1 | 17,34 | 32,00 | 80,00 | 111,00 | 142,66 |
| 2 | 1,96 | 4,65 | 12,80 | 24,30 | 45,00 |
| 3 | 5,00 | 7,00 | 9,00 | 9,60 | 9,94 |
| 4 | 1,20 | 2,90 | 7,25 | 10,20 | 13,15 |
| 5 | 2,40 | 3,60 | 14,40 | 28,80 | 67,20 |
| 6 | 96,00 | 132,00 | 174,00 | 198,00 | 246,00 |
| Таблица 4 | |||||
| Числовые значения показателей для эксперта №2 | |||||
| № показателя | Значения показателя | ||||
| Ui21(gi)=0,10 | Ui22(gi)=0,20 | Ui23(gi)=0,50 | Ui24(gi)=0,70 | Ui25(gi)=0,90 | |
| 1 | 16,18 | 30,05 | 77,34 | 108,00 | 134,68 |
| 2 | 0,27 | 1,33 | 6,65 | 13,99 | 31,33 |
| 3 | 1,60 | 2,80 | 6,10 | 8,00 | 9,24 |
| 4 | 1,00 | 2,30 | 6,00 | 8,60 | 11,20 |
| 5 | 5,60 | 9,60 | 28,80 | 45,60 | 84,00 |
| 6 | 90,00 | 120,00 | 157,00 | 180,00 | 240,00 |
| Таблица 5 | |||||
| Числовые значения показателей для эксперта №3 | |||||
| № показателя | Значения показателя | ||||
| Ui31(gi)=0,10 | Ui32(gi)=0,20 | Ui33(gi)=0,50 | Ui34(gi)=0,70 | Ui35(gi)=0,90 | |
| 1 | 9,54 | 18,00 | 52,00 | 73,35 | 96,00 |
| 2 | 1,12 | 2,98 | 10,00 | 20,00 | 38,67 |
| 3 | 2,60 | 4,10 | 7,60 | 8,80 | 9,52 |
| 4 | 1,30 | 3,20 | 8,95 | 11,40 | 14,70 |
| 5 | 4,00 | 6,60 | 20,40 | 38,40 | 74,40 |
| 6 | 36,00 | 60,00 | 102,00 | 132,00 | 198,00 |
| Таблица 6 | |||||
| Числовые значения показателей для эксперта №4 | |||||
| № показателя | Значения показателя | ||||
| Ui41(gi)=0,10 | Ui42(gi)=0,20 | Ui43(gi)=0,50 | Ui44(gi)=0,70 | Ui45(gi)=0,90 | |
| 1 | 12,66 | 22,10 | 61,33 | 90,00 | 117,34 |
| 2 | 4,48 | 9,66 | 22,65 | 41,33 | 60,00 |
| 3 | 2,00 | 3,40 | 6,80 | 8,40 | 9,38 |
| 4 | 1,10 | 2,60 | 6,60 | 9,30 | 12,20 |
| 5 | 7,20 | 12,50 | 36,00 | 57,60 | 93,60 |
| 6 | 135,00 | 165,00 | 204,00 | 234,00 | 270,00 |
| Таблица 7 | |||||
| Числовые значения показателей для эксперта №5 | |||||
| № показателя | Значения показателя | ||||
| Ui51(gi)=0,10 | Ui52(gi)=0,20 | Ui53(gi)=0,50 | Ui54(gi)=0,70 | Ui55(gi)=0,90 | |
| 1 | 8,00 | 20,10 | 46,65 | 66,62 | 86,65 |
| 2 | 2,80 | 6,32 | 18,10 | 30,00 | 54,00 |
| 3 | 1,20 | 2,40 | 5,40 | 7,38 | 9,10 |
| 4 | 1,40 | 3,50 | 8,70 | 12,30 | 16,50 |
| 5 | 10,40 | 18,60 | 48,00 | 72,00 | 103,20 |
| 6 | 114,00 | 150,00 | 188,00 | 216,00 | 258,00 |
| Таблица 8 | |||||
| Числовые значения показателей для эксперта №6 | |||||
| № показателя | Значения показателя | ||||
| Ui61(gi)=0,10 | Ui62(gi)=0,20 | Ui63(gi)=0,50 | Ui64(gi)=0,70 | Ui65(gi)=0,90 | |
| 1 | 14,22 | 24,00 | 63,20 | 98,20 | 125,40 |
| 2 | 3,64 | 7,99 | 22,10 | 36,00 | 57,34 |
| 3 | 3,00 | 4,80 | 8,20 | 9,15 | 9,68 |
| 4 | 1,50 | 3,80 | 9,60 | 13,50 | 17,70 |
| 5 | 12,00 | 21,60 | 55,20 | 79,30 | 108,00 |
| 6 | 72,00 | 102,00 | 144,00 | 165,00 | 234,00 |
| Таблица 9 | |||||
| Числовые значения показателей для эксперта №7 | |||||
| № показателя | Значения показателя | ||||
| Ui71(gi)=0,10 | Ui72(gi)=0,20 | Ui73(gi)=0,50 | Ui74(gi)=0,70 | Ui75(gi)=0,90 | |
| 1 | 11,10 | 19,80 | 57,34 | 98,67 | 125,30 |
| 2 | 5,32 | 11,33 | 30,00 | 45,30 | 61,38 |
| 3 | 3,60 | 6,00 | 8,80 | 9,40 | 9,80 |
| 4 | 0,90 | 2,00 | 5,40 | 7,95 | 10,20 |
| 5 | 8,80 | 15,60 | 40,00 | 64,80 | 100,80 |
| 6 | 54,00 | 81,00 | 123,00 | 150,00 | 222,00 |
| Таблица 10 | |||||
| Средние значения показателей на основе информации от семи экспертов | |||||
| № показателя | Средние значения показателей | ||||
| Ui1(gi)=0,10 | Ui2(gi)=0,20 | Ui3(gi)=0,50 | Ui4(gi)=0,70 | Ui5(gi)=0,90 | |
| 1 | 12,72 | 23,72 | 62,69 | 92,26 | 118,29 |
| 2 | 2,80 | 6,32 | 17,47 | 30,15 | 49,67 |
| 3 | 2,71 | 4,36 | 7,41 | 8,68 | 9,38 |
| 4 | 1,20 | 2,90 | 7,50 | 10,46 | 13,66 |
| 5 | 7,20 | 12,59 | 34,69 | 55,21 | 90,17 |
| 6 | 91,00 | 115,72 | 156,00 | 182,14 | 238,29 |
| Таблица 11 | |||||
| Разности между средними величинами единичного показателя и значениями этого показателя по мнению эксперта №1 | |||||
| № показателя | Значения разности | ||||
| Ui11(gi)=0,10 | Ui12(gi)=0,20 | Ui13(gi)=0,50 | Ui14(gi)=0,70 | Ui15(gi)=0,90 | |
| 1 | 4,62 | 8,28 | 17,31 | 18,74 | 24,37 |
| 2 | 0,84 | 1,67 | 8,47 | 5,85 | 4,67 |
| 3 | 2,29 | 2,64 | 1,59 | 0,92 | 0,56 |
| 4 | 0,00 | 0,00 | 0,25 | 0,26 | 0,51 |
| 5 | 4,80 | 8,99 | 10,29 | 26,41 | 22,97 |
| 6 | 5,00 | 16,28 | 18,00 | 15,86 | 7,71 |
| Таблица 12 | |||||
| Разности между средними величинами единичного показателя и значениями этого показателя по мнению эксперта №2 | |||||
| № показателя | Значения разности | ||||
| Ui21(gi)=0,10 | Ui22(gi)=0,20 | Ui23(gi)=0,50 | Ui24(gi)=0,70 | Ui25(gi)=0,90 | |
| 1 | 3,46 | 6,33 | 14,65 | 15,74 | 16,39 |
| 2 | 2,53 | 4,99 | 10,82 | 16,16 | 18,34 |
| 3 | 1,11 | 1,56 | 1,31 | 0,68 | 0,14 |
| 4 | 0,20 | 0,60 | 1,50 | 1,86 | 2,46 |
| 5 | 1,60 | 2,99 | 5,89 | 9,61 | 6,17 |
| 6 | 1,00 | 4,28 | 1,00 | 2,14 | 1,71 |
| Таблица 13 | |||||
| Разности между средними величинами единичного показателя и значениями этого показателя по мнению эксперта №3 | |||||
| № показателя | Значения разности | ||||
| Ui31(gi)=0,10 | Ui32(gi)=0,20 | Ui33(gi)=0,50 | Ui34(gi)=0,70 | Ui35(gi)=0,90 | |
| 1 | 3,18 | 5,72 | 10,69 | 18,91 | 22,29 |
| 2 | 1,68 | 3,34 | 7,47 | 10,15 | 11,00 |
| 3 | 0,11 | 0,26 | 0,19 | 0,12 | 0,14 |
| 4 | 0,10 | 0,30 | 1,45 | 0,94 | 1,04 |
| 5 | 3,20 | 5,99 | 14,29 | 16,81 | 15,77 |
| 6 | 55,00 | 55,72 | 54,00 | 50,14 | 40,29 |
| Таблица 14 | |||||
| Разности между средними величинами единичного показателя и значениями этого показателя по мнению эксперта №4 | |||||
| № показателя | Значения разности | ||||
| Ui41(gi)=0,10 | Ui42(gi)=0,20 | Ui43(gi)=0,50 | Ui44(gi)=0,70 | Ui45(gi)=0,90 | |
| 1 | 0,06 | 1,62 | 1,36 | 2,26 | 0,95 |
| 2 | 1,68 | 3,34 | 5,18 | 11,18 | 10,33 |
| 3 | 0,71 | 0,96 | 0,61 | 0,28 | 0,00 |
| 4 | 0,10 | 0,30 | 0,90 | 1,16 | 1,46 |
| 5 | 0,00 | 0,09 | 1,31 | 2,39 | 3,43 |
| 6 | 44,00 | 50,28 | 48,00 | 51,86 | 31,71 |
| Таблица 15 | |||||
| Разности между средними величинами единичного показателя и значениями этого показателя по мнению эксперта №5 | |||||
| № показателя | Значения разности | ||||
| Ui51(gi)=0,10 | Ui52(gi)=0,20 | Ui53(gi)=0,50 | Ui54(gi)=0,70 | Ui55(gi)=0,90 | |
| 1 | 4,72 | 3,62 | 16,04 | 25,64 | 31,64 |
| 2 | 0,00 | 0,00 | 0,63 | 0,15 | 4,33 |
| 3 | 1,51 | 1,96 | 2,01 | 1,30 | 0,28 |
| 4 | 0,20 | 0,60 | 1,20 | 1,84 | 2,84 |
| 5 | 3,20 | 6,01 | 13,31 | 26,79 | 13,03 |
| 6 | 23,00 | 34,28 | 32,00 | 33,86 | 19,71 |
| Таблица 16 | |||||
| Разности между средними величинами единичного показателя и значениями этого показателя по мнению эксперта №6 | |||||
| № показателя | Значения разности | ||||
| Ui61(gi)=0,10 | Ui62(gi)=0,20 | Ui63(gi)=0,50 | Ui64(gi)=0,70 | Ui65(gi)=0,90 | |
| 1 | 1,50 | 0,28 | 0,51 | 5,94 | 7,11 |
| 2 | 0,84 | 1,67 | 4,63 | 5,85 | 7,67 |
| 3 | 0,29 | 0,44 | 0,79 | 0,47 | 0,30 |
| 4 | 0,30 | 0,90 | 2,10 | 3,04 | 4,04 |
| 5 | 4,80 | 9,01 | 20,51 ' | 24,09 | 17,83 |
| 6 | 19,00 | 13,72 | 12,00 | 17,14 | 4,29 |
| Таблица 17 | |||||
| Разности между средними величинами единичного показателя и значениями этого показателя по мнению эксперта №7 | |||||
| № показателя | Значения разности | ||||
| Ui71(gi)=0,10 | Ui72(gi)=0,20 | Ui73(gi)=0,50 | Ui74(gi)=0,70 | Ui75(gi)=0,90 | |
| 1 | 1,62 | 3,92 | 5,35 | 6,41 | 7,01 |
| 2 | 2,52 | 5,01 | 12,53 | 15,15 | 11,71 |
| 3 | 0,89 | 1,64 | 1,39 | 0,72 | 0,42 |
| 4 | 0,30 | 0,90 | 2,10 | 2,51 | 3,46 |
| 5 | 1,60 | 3,01 | 5,31 | 9,59 | 10,63 |
| 6 | 37,00 | 34,72 | 33,00 | 32,14 | 16,29 |
| Таблица 18 | |||||
| Нормированные значения разности для эксперта №1 | |||||
| № показателя | Нормированные значения разности | ||||
| Ui11(gi)=0,10 | Ui12(gi)=0,20 | Ui13(gi)=0,50 | Ui14(gi)=0,70 | Ui15(gi)=0,90 | |
| 1 | 0,363 | 0,349 | 0,276 | 0,203 | 0,206 |
| 2 | 0,300 | 0,264 | 0,485 | 0,194 | 0,094 |
| 3 | 0,845 | 0,606 | 0,215 | 0,106 | 0,060 |
| 4 | 0,000 | 0,000 | 0,033 | 0,025 | 0,037 |
| 5 | 0,667 | 0,714 | 0,297 | 0,478 | 0,255 |
| 6 | 0,055 | 0,141 | 0,115 | 0,087 | 0,032 |
| Таблица 19 | |||||
| Нормированные значения разности для эксперта №2 | |||||
| № показателя | Нормированные значения разности | ||||
| Ui21(gi)=0,10 | Ui22(gi)=0,20 | Ui23(gi)=0,50 | Ui24(gi)=0,70 | Ui25(gi)=0,90 | |
| 1 | 0,272 | 0,267 | 0,234 | 0,171 | 0,139 |
| 2 | 0,904 | 0,790 | 0,619 | 0,536 | 0,369 |
| 3 | 0,410 | 0,357 | 0,176 | 0,078 | 0,015 |
| 4 | 0,167 | 0,207 | 0,200 | 0,178 | 0,180 |
| 5 | 0,222 | 0,237 | 0,170 | 0,174 | 0,068 |
| 6 | 0,011 | 0,037 | 0,006 | 0,012 | 0,007 |
| Таблица 20 | |||||
| Нормированные значения разности для эксперта №3 | |||||
| № показателя | Нормированные значения разности | ||||
| Ui31(gi)=0,10 | Ui32(gi)=0,20 | Ui33(gi)=0,50 | Ui34(gi)=0,70 | Ui35(gi)=0,90 | |
| 1 | 0,250 | 0,241 | 0,171 | 0,205 | 0,188 |
| 2 | 0,600 | 0,528 | 0,428 | 0,337 | 0,221 |
| 3 | 0,041 | 0,060 | 0,026 | 0,014 | 0,015 |
| 4 | 0,083 | 0,103 | 0,193 | 0,090 | 0,076 |
| 5 | 0,444 | 0,476 | 0,412 | 0,304 | 0,175 |
| 6 | 0,604 | 0,482 | 0,346 | 0,275 | 0,169 |
| Таблица 21 | |||||
| Нормированные значения разности для эксперта №4 | |||||
| № показателя | Нормированные значения разности | ||||
| Ui41(gi)=0,10 | Ui42(gi)=0,20 | Ui43(gi)=0,50 | Ui44(gi)=0,70 | Ui45(gi)=0,90 | |
| 1 | 0,005 | 0,068 | 0,022 | 0,024 | 0,008 |
| 2 | 0,600 | 0,528 | 0,297 | 0,371 | 0,208 |
| 3 | 0,262 | 0,220 | 0,082 | 0,032 | 0,000 |
| 4 | 0,083 | 0,103 | 0,120 | 0,111 | 0,107 |
| 5 | 0,000 | 0,007 | 0,038 | 0,043 | 0,038 |
| 6 | 0,484 | 0,434 | 0,308 | 0,285 | 0,133 |
| Таблица 22 | |||||
| Нормированные значения разности для эксперта №5 | |||||
| № показателя | Нормированные значения разности | ||||
| Ui51(gi)=0,10 | Ui52(gi)=0,20 | Ui53(gi)=0,50 | Ui54(gi)=0,70 | Ui55(gi)=0,90 | |
| 1 | 0,371 | 0,153 | 0,256 | 0,278 | 0,267 |
| 2 | 0,000 | 0,000 | 0,036 | 0,005 | 0,087 |
| 3 | 0,557 | 0,450 | 0,271 | 0,150 | 0,030 |
| 4 | 0,167 | 0,207 | 0,160 | 0,176 | 0,208 |
| 5 | 0,444 | 0,477 | 0,384 | 0,485 | 0,145 |
| 6 | 0,253 | 0,296 | 0,205 | 0,186 | 0,083 |
| Таблица 23 | |||||
| Нормированные значения разности для эксперта №6 | |||||
| № показателя | Нормированные значения разности | ||||
| Ui61(gi)=0,10 | Ui62(gi)=0,20 | Ui63(gi)=0,50 | Ui64(gi)=0,70 | Ui65(gi)=0,90 | |
| 1 | 0,118 | 0,012 | 0,008 | 0,064 | 0,060 |
| 2 | 0,300 | 0,264 | 0,265 | 0,194 | 0,154 |
| 3 | 0,107 | 0,101 | 0,107 | 0,054 | 0,032 |
| 4 | 0,250 | 0,310 | 0,280 | 0,291 | 0,296 |
| 5 | 0,667 | 0,716 | 0,591 | 0,436 | 0,198 |
| 6 | 0,209 | 0,119 | 0,077 | 0,094 | 0,018 |
| Таблица 24 | |||||
| Нормированные значения разности для эксперта №7 | |||||
| № показателя | Нормированные значения разности | ||||
| Ui71(gi)=0,10 | Ui72(gi)=0,20 | Ui73(gi)=0,50 | Ui74(gi)=0,70 | Ui75(gi)=0,90 | |
| 1 | 0,127 | 0,165 | 0,085 | 0,069 | 0,059 |
| 2 | 0,900 | 0,793 | 0,717 | 0,502 | 0,236 |
| 3 | 0,328 | 0,376 | 0,188 | 0,083 | 0,045 |
| 4 | 0,250 | 0,310 | 0,280 | 0,240 | 0,253 |
| 5 | 0,222 | 0,239 | 0,153 | 0,174 | 0,118 |
| 6 | 0,411 | 0,300 | 0,212 | 0,176 | 0,068 |
| Таблица 25 | |||||
| Квадраты нормированных значений разности для эксперта №1 | |||||
| № показателя | Квадраты нормированных значений разности | ||||
| Ui11(gi)=0,10 | Ui12(gi)=0,20 | Ui13(gi)=0,50 | Ui14(gi)=0,70 | Ui15(gi)=0,90 | |
| 1 | 0,1318 | 0,1218 | 0,0762 | 0,0412 | 0,0424 |
| 2 | 0,0900 | 0,0697 | 0,2350 | 0,0376 | 0,0088 |
| 3 | 0,7141 | 0,3666 | 0,0460 | 0,0112 | 0,0036 |
| 4 | 0,0000 | 0,0000 | 0,0011 | 0,0006 | 0,0014 |
| 5 | 0,4444 | 0,5099 | 0,0880 | 0,2288 | 0,0649 |
| 6 | 0,0030 | 0,0198 | 0,0133 | 0,0076 | 0,0010 |
| Таблица 26 | |||||
| Квадраты нормированных значений разности для эксперта №2 | |||||
| № показателя | Квадраты нормированных значений разности | ||||
| Ui21(gi)=0,10 | Ui22(gi)=0,20 | Ui23(gi)=0,50 | Ui24(gi)=0,70 | Ui25(gi)=0,90 | |
| 1 | 0,0740 | 0,0712 | 0,0546 | 0,0291 | 0,0192 |
| 2 | 0,8164 | 0,6234 | 0,3836 | 0,2873 | 0,1363 |
| 3 | 0,1678 | 0,1280 | 0,0313 | 0,0061 | 0,0002 |
| 4 | 0,0278 | 0,0428 | 0,0400 | 0,0316 | 0,0324 |
| 5 | 0,0494 | 0,0564 | 0,0288 | 0,0303 | 0,0047 |
| 6 | 0,0001 | 0,0014 | 0,00004 | 0,0001 | 0,00005 |
| Таблица 27 | |||||
| Квадраты нормированных значений разности для эксперта №3 | |||||
| № показателя | Квадраты нормированных значений разности | ||||
| Ui31(gi)=0,10 | Ui32(gi)=0,20 | Ui33(gi)=0,50 | Ui34(gi)=0,70 | Ui35(gi)=0,90 | |
| 1 | 0,0625 | 0,0582 | 0,0291 | 0,0420 | 0,0355 |
| 2 | 0,3600 | 0,2793 | 0,1828 | 0,1133 | 0,0490 |
| 3 | 0,0016 | 0,0036 | 0,0007 | 0,0002 | 0,0002 |
| 4 | 0,0007 | 0,0107 | 0,0374 | 0,0081 | 0,0058 |
| 5 | 0,1975 | 0,2264 | 0,1697 | 0,0927 | 0,0306 |
| 6 | 0,3653 | 0,2318 | 0,1198 | 0,0758 | 0,0286 |
| Таблица 28 | |||||
| Квадраты нормированных значений разности для эксперта №4 | |||||
| № показателя | Квадраты нормированных значений разности | ||||
| Ui41(gi)=0,10 | Ui42(gi)=0,20 | Ui43(gi)=0,50 | Ui44(gi)=0,70 | Ui45(gi)=0,90 | |
| 1 | 0,00002 | 0,0047 | 0,0005 | 0,0006 | 0,00006 |
| 2 | 0,3600 | 0,2793 | 0,0879 | 0,1375 | 0,0436 |
| 3 | 0,0686 | 0,0485 | 0,0068 | 0,0010 | 0,0000 |
| 4 | 0,0069 | 0,0107 | 0,0144 | 0,0123 | 0,0114 |
| 5 | 0,0000 | 0,00005 | 0,0014 | 0,0019 | 0,0014 |
| 6 | 0,2338 | 0,1888 | 0,0947 | 0,0811 | 0,0177 |
| Таблица 29 | |||||
| Квадраты нормированных значений разности для эксперта №5 | |||||
| № показателя | Квадраты нормированных значений разности | ||||
| Ui51(gi)=0,10 | Ui52(gi)=0,20 | Ui53(gi)=0,50 | Ui54(gi)=0,70 | Ui55(gi)=0,90 | |
| 1 | 0,1377 | 0,0230 | 0,0655 | 0,0772 | 0,0715 |
| 2 | 0,0000 | 0,0000 | 0,0013 | 0,00002 | 0,0076 |
| 3 | 0,0964 | 0,2021 | 0,0736 | 0,0224 | 0,0009 |
| 4 | 0,0278 | 0,0428 | 0,0256 | 0,0309 | 0,0432 |
| 5 | 0,1975 | 0,2279 | 0,1472 | 0,2355 | 0,0209 |
| 6 | 0,0639 | 0,0878 | 0,0421 | 0,0346 | 0,0068 |
| Таблица 30 | |||||
| Квадраты нормированных значений разности для эксперта №6 | |||||
| № показателя | Квадраты нормированных значений разности | ||||
| Ui61(gi)=0,10 | Ui62(gi)=0,20 | Ui63(gi)=0,50 | Ui64(gi)=0,70 | Ui65(gi)=0,90 | |
| 1 | 0,0139 | 0,0001 | 0,00007 | 0,0041 | 0,0036 |
| 2 | 0,0900 | 0,0698 | 0,0702 | 0,0376 | 0,0238 |
| 3 | 0,0115 | 0,0102 | 0,0114 | 0,0029 | 0,0010 |
| 4 | 0,0625 | 0,0963 | 0,0784 | 0,0845 | 0,0875 |
| 5 | 0,4444 | 0,5122 | 0,3496 | 0,1904 | 0,0391 |
| 6 | 0,0436 | 0,0141 | 0,0059 | 0,0089 | 0,0003 |
| Таблица 31 | |||||
| Квадраты нормированных значений разности для эксперта №7 | |||||
| № показателя | Квадраты нормированных значений разности | ||||
| Ui71(gi)=0,10 | Ui72(gi)=0,20 | Ui73(gi)=0,50 | Ui74(gi)=0,70 | Ui75(gi)=0,90 | |
| 1 | 0,0162 | 0,0273 | 0,0073 | 0,0048 | 0,0035 |
| 2 | 0,8100 | 0,6284 | 0,5144 | 0,2525 | 0,0556 |
| 3 | 0,1079 | 0,1415 | 0,0352 | 0,0069 | 0,0020 |
| 4 | 0,0625 | 0,0963 | 0,0784 | 0,0576 | 0,0642 |
| 5 | 0,0494 | 0,0572 | 0,0234 | 0,0302 | 0,0139 |
| 6 | 0,1690 | 0,0900 | 0,0447 | 0,0311 | 0,0047 |
| Таблица 32 | |||||
| Итоги суммирования и оценки Wj | |||||
| Промежуточные величины | № показателя | Суммы квадратов нормированных значений разности | |||
| Ui1(gi)=0,10 | Ui2(gi)=0,20 | Ui3(gi)=0,50 | Ui4(gi)=0,70 | Ui5(gi)=0,90 | |
| 1 | 0,4361 | 0,3063 | 0,2332 | 0,1990 | 0,1757 |
| 2 | 2,5264 | 1,9499 | 1,4752 | 0,8658 | 0,3247 |
| 3 | 1,1679 | 0,9005 | 0,2050 | 0,0507 | 0,0079 |
| 4 | 0,1882 | 0,2996 | 0,2753 | 0,2256 | 0,2459 |
| 5 | 1,3826 | 1,5900 | 0,8081 | 0,8098 | 0,1755 |
| 6 | 0,8787 | 0,6337 | 0,3205 | 0,2392 | 0,0591 |
| Σ | 6,5799 | 5,6800 | 3,3173 | 2,3901 | 0,9888 |
| Wj | 0,9923 | 0,9938 | 0,9961 | 0,9972 | 0,9988 |
состоит из 5×n элементов, первую группу блоков деления, состоящую из 5×n элементов, вторую группу блоков деления, включающую m матриц, каждая из которых состоит из 5×n элементов, первую группу ЭЗ, включающую пять подгрупп, каждая из которых состоит из n элементов, вторую и третью группы ЭЗ, состоящие из четырех элементов, группу регистров, состоящую из 5×n элементов, первую группу ключей, состоящую из 5×n элементов, вторую группу ключей, состоящую из пяти элементов, регистр, группу квадраторов, включающую m матриц, каждая из которых состоит из 5×n элементов, элемент ИЛИ, блок сравнения, блок деления, первую группу блоков индикации, состоящую из 5×n элементов, вторую группу блоков индикации, состоящую из n элементов, генератор тактовых импульсов и распределитель импульсов (РИ), тактовый вход которого соединен с выходом генератора тактовых импульсов, первый выход РИ - со входами записи первой группы входных регистров, второй, третий и четвертый выходы - со входами записи соответственно первого, второго и третьего входных регистров, пятый выход - со входами считывания группы входных регистров, шестой выход - с управляющими входами группы коммутаторов, седьмой выход - со входами записи группы регистров, восьмой выход - со входом считывания второго регистра, девятый выход - с управляющим входом коммутатора, десятый и одиннадцатый выходы - со входами считывания соответственно первого и третьего входных регистров, с двенадцатого по шестнадцатый выходы - с управляющими входами соответственно с первого по пятый элементов второй группы ключей, семнадцатый выход - со входами считывания группы регистров, восемнадцатый и девятнадцатый выходы - со входами соответственно записи и считывания регистра, информационные входы группы входных регистров являются входом задания исходной информации, на которые поступают значения giкj, характеризующие i-й единичный показатель для к-го эксперта j-й точки его функции ценности, информационные входы первого, второго и третьего входных регистров являются входом задания исходной информации, на который поступают соответственно значения n, m и W∂, характеризующие количество единичных показателей, число экспертов и допустимое значение коэффициента конкордации, выход каждого элемента с первой по m-ую матрицы входного регистра соединен с информационным входом соответствующего элемента с первой по m-ую матрицы группы коммутаторов, первый выход каждого из которых подключен к первому по m-й входы соответствующих элементов первой группы сумматоров с накоплением, а второй выход - к входу вычитаемого соответствующего элемента каждой из m матриц группы блоков вычитания, выход каждого из которых соединен с входом делимого соответствующего элемента каждой из m матриц второй группы блоков деления, а вход уменьшаемого каждой матрицы - с выходом соответствующего элемента единственной матрицы первой группы блоков деления, вход делимого каждого из которых подключен к выходу соответствующего элемента первой группы сумматоров с накоплением, а вход делителя - к первому выходу коммутатора, второй выход которого соединен с входом квадратора, а информационный вход - с выходом второго входного регистра, выход первого входного регистра подключен к входам блока возведения в степень и ЭЗ, выходы которых соединены с входами соответственно уменьшаемого и вычитаемого первого блока вычитания, выход которого подключен к первому входу первого блока умножения, второй вход которого соединен с выходом квадратора, а выход - с информационным входом регистра, выход которого подключен к входу делителя блока деления, вход делимого которого соединен с выходом второго блока умножения, а выход - с входом вычитаемого второго блока вычитания, выход которого подключен к информационному входу блока сравнения, пороговый вход которого соединен с выходом третьего входного регистра, выход каждого элемента первой группы блоков деления подключен к информационному входу соответствующего элемента группы регистров и к входу соответствующего элемента первой группы ЭЗ, выход каждого из которых соединен с входом делителя соответствующего элемента каждой из m матриц второй группы блоков деления, выход каждого из которых подключен к входу каждого соответствующего элемента группы квадраторов, выход каждого из которых соединен с первым по m-й входом соответствующих элементов второй группы сумматоров с накоплением, выход каждого элемента определенного столбца которой подключен к первому по n-й входы соответствующих элементов третьей группы сумматоров с накоплением, выход первого элемента которой соединен с первым входом элемента ИЛИ, а вход каждого из последующих элементов, со второго по пятый, - с входом соответствующего элемента, с первого по четвертый, второй группы ЭЗ, выход каждого из которых подключен к соответствующим входам элемента ИЛИ, со второго по пятый выход которого соединен с входом второго блока умножения, выход блока сравнения подключен к информационному входу каждого элемента второй группы ключей, выход последнего, пятого, из которой соединен с управляющим входом каждого элемента последнего, пятого, столбца первой группы ключей, выход каждого из остальных элементов, с первого по четвертый, второй группы ключей подключен к входу соответствующего элемента третьей группы ЭЗ, выход каждого из которых соединен с управляющим входом каждого элемента соответствующего столбца, с первого по четвертый, первой группы ключей, информационный вход каждого элемента которой подключен к выходу соответствующего элемента группы регистров, а выход - к входу соответствующего элемента первой группы блоков индикации, при этом выходы элементов определенной строки, с первой по n-ую, первой группы ключей соединены с первым по пятый входы соответствующих элементов, с первого по n-й, второй группы блоков индикации.
На фиг.1-6 изображены функции ценности для шести единичных оценочных показателей, характеризующие грузовой автомобиль. Номера кривых на каждой фигуре соответствуют номерам соответствующих экспертов (от первого до седьмого).
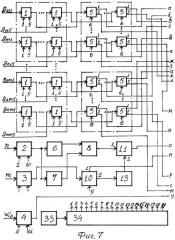
На фиг.7, 8, 9 и 10 представлена функциональная схема у