Способ автоматического декодирования изображений микроматрицы

Способ автоматического декодирования изображений микроматрицы

Иллюстрации

Показать все

Реферат

Перекрестные ссылки на родственные заявки

Заявители притязают на приоритет предварительной заявки № 60/868129, поданной 1 декабря 2006 г.

Данное изобретение относится к способу автоматического определения положений зондов в изображении микроматрицы, чтобы данные изображения можно было преобразовать в меры биологической активности.

Технология микроматриц ДНК разработана недавно и быстро развивается. В настоящее время она широко используется в систематических исследованиях глобальных программ экспрессии генов, при выявлении функции генов с использованием микроматриц, при измерении полиморфизмов числа копий гена и взаимодействий ДНК-белок в пределах генома. Извлечение данных из изображений микроматрицы сопряжено с многочисленными внутренними проблемами: неоднородная гибридизация приводит к неравномерности интенсивности и геометрии зонда; размещение чипов в сканере не фиксируется, в результате чего углы чипа могут находиться где угодно; сканеры часто искажают результирующие изображения, и это затрудняет преобразование этих изображений в необходимые данные; опорные точки могут располагаться во многих разных комбинациях, поскольку одновременно существует много разных шаблонов конструкции.

Микроматрица ДНК состоит из твердой поверхности, с которой химически связаны одноцепочечные молекулы ДНК. Микроматрицы широко используются для изучения экспрессии генов с целью связывания активностей генов с биологическими процессами и группирования генов в сети взаимосвязанных активностей. Они обладают большими преимуществами, поскольку позволяют параллельно измерять экспрессию тысяч генов в полуавтоматическом режиме. В функциональной геномике существуют разные типы микроматриц, в том числе матрицы экспрессии генов, матрицы для анализа однонуклеотидного полиморфизма (SNP), матрицы генных промоторов, матрицы сравнительной геномной гибридизации, матрицы ЦГ-богатых островков и т.д. Для всех этих типов матриц сканированное изображение необходимо обрабатывать для нахождения данных микроматрицы.

Репрезентативный анализ олигонуклеотидной микроматрицы (ROMA) был разработан в лаборатории Cold Spring Harbor Laboratory (CSHL) в качестве варианта способа сравнительной геномной гибридизации [6]. Эта технология является значительным шагом вперед в разрешении, доступном для исследования полиморфизмов числа копий (CNP) в геноме человека. Благодаря классификации генома с помощью фермента с малым (6 пар оснований) участком распознавания, формируется большое количество фрагментов, более или менее равномерно распределенных по геному. В каждом фрагменте, уникальный зонд был идентифицирован и размещен в одном пятне на микроматрице. В настоящее время используются чипы с 85000 зондов, и чипы с примерно 400000 зондами находятся на стадии тестирования. ДНК, извлеченная из клеток ткани-образца, маркируется и гибридизируется с помощью чипа; изменения интенсивности пропорциональны числам копий фрагментов в образцах. Благодаря использованию этой методологии можно идентифицировать изменение между раковым и нормальным геномами, а также между нормальными человеческими геномами.

Однако эти чипы высокой плотности представляют проблему для современных устройств чтения чипов. С использованием шаговых двигателей и лазерных сканеров возбужденные гибридизированные зонды преобразуются в изображения, т.е. пиксельные матрицы. Двигатель каждый раз перемещает сканер на несколько микрон, обеспечивая считывание новой строки. Таким образом, производится оцифровка чипа микроматрицы с различными разрешениями в один, два или пять микрон в зависимости от величины шага двигателя. Матрица зондов в изображении подвергается параллельному переносу и повороту неизвестной величины за счет механических и оптических операций сканера. Кроме того, может возникать эффект трапецеидального искажения (т.е. матрица приобретает трапецеидальную форму вместо прямоугольной) и/или малые синусоидальные возмущения в положениях зондов (т.е. вместо того, чтобы располагаться на прямой линии, зонды в действительности располагаются на синусоидальной кривой). Для исследования с высокой пропускной способностью с помощью микроматриц высокой плотности требуется программное обеспечение для автоматической (т.е. без вмешательства человека) идентификации положения зондов, интенсивности которых подлежат преобразованию в интенсивности зондов.

В настоящее время шаблоны зондов на чипах исследуются, но максимальная плотность достигается при шахматном шаблоне. Таким образом, половина площади чипа пропадает впустую, поскольку современное программное обеспечение обработки изображения не способно адекватно разрешать зонды. Если будет создано усовершенствованное программное обеспечение, можно будет добиться удвоения плотности информации на чипах ROMA.

В литературе описаны другие алгоритмы, которые пытаются осуществлять автоматический анализ изображения микроматрицы. В работах Brandle и др. [ссылка 1] и Uehara и Kakadiaris [ссылка 6] представлены подходы ко всему спектру функций, необходимых для преобразования изображения в нужные численные значения, и рекомендуется использовать преобразование Радона (см. ниже), но насколько нам известно, подход к коррекции трапецеидального искажения в изображениях микроматрицы до сих пор не предложен. Программное средство BioDiscovery Imagene 7.0 претендует на автоматическое нахождение пятен и размещение сетки даже в пакетном режиме обработки для множественных матриц, однако алгоритмы на данный момент не обнародованы (http://www.biodiscovery.com/index/imagene-cgh). В работе Khojasteh и др. [ссылка 2] предложен алгоритм автоматической идентификации областей выигрыша и потери числа копий ДНК из данных CGH матрицы посредством алгоритма определения края с множественным масштабированием [2].

Решить эти проблемы позволяет раскрытый здесь способ, который предусматривает автоматическую идентификацию углов и зондов из сканированного изображения микроматрицы. Пробные изображения получены с помощью технологии микроматриц ROMA, но способ является достаточно общим, чтобы работать с другими типами изображений микроматрицы.

Согласно настоящему изобретению раскрыт способ автоматической идентификации углов и зондов чипа микроматрицы в сканированном изображении микроматрицы высокой плотности и высокого разрешения, имеющем пространство изображения, в котором способ минимизирует ошибочные искажения в изображении, возникающие в процессе сканирования, путем применения к изображению многопроходного алгоритма нахождения углов.

В частности, задачей этого изобретения является обеспечение способа автоматической идентификации углов и зондов чипа микроматрицы, даже в отсутствие самих зондов в углах, в сканированном изображении микроматрицы высокой плотности и высокого разрешения, имеющем пространство изображения, в котором способ минимизирует ошибочные искажения в изображении, возникающие в процессе сканирования, путем применения к изображению многопроходного алгоритма нахождения углов и содержит этапы, на которых:

применяют преобразование Радона к входному изображению микроматрицы для проецирования изображения в пространство углов и расстояний, когда это возможно, для нахождения ориентации прямых линий,

применяют быстрое преобразование Фурье к спроецированному изображению, полученному на этапе (a), для нахождения оптимального угла наклона спроецированного изображения,

определяют оптимальные первый и последний локальные максимумы для оптимального угла наклона,

выполняют обратную проекцию определенных первого и последнего локальных максимумов в пространство изображения для нахождения, в первом приближении, первой и последней вертикальных линий изображения,

поворачивают изображение и повторяют этапы (a)-(d) для нахождения, в первом приближении, верхней и нижней горизонтальных линий изображения,

определяют, в первом приближении, четыре угла изображения из пересечения вертикальных и горизонтальных линий,

применяют эвристику для определения, достаточно ли первого приближения, полученного на этапе (f), и,

опционально, обрезают сканированное изображение вокруг первого приближения четырех углов и повторяют этапы (a)-(f).

Еще одной задачей является обеспечение способа, в котором сканированное изображение микроматрицы представляет собой изображение, полученное посредством элемента, выбранного из группы, состоящей из репрезентативного анализа олигонуклеотидной микроматрицы, матриц экспрессии генов, матриц однонуклеотидного полиморфизма, матриц ЦГ-богатых островков, микроматриц промоторов и матриц взаимодействия белок-ДНК.

Еще одной задачей является обеспечение способа, в котором ошибочные искажения в изображении включают в себя эффекты трапецеидального искажения.

Еще одной задачей является обеспечение способа, в котором ошибочные искажения в изображении включают в себя синусоидальные или искривленные линии размещения зондов вместо прямых линий размещения.

Еще одной задачей является обеспечение способа, в котором разрешение сканированного изображения составляет 1, 2 или 5 микрон.

Еще одной задачей является обеспечение способа, в котором сканированное изображение сканируют с использованием флуорофоров Cy3 и Cy5.

Еще одной задачей является обеспечение способа, в котором сканированное изображение получают из чипа, содержащего от около 85000 зондов до около 400000 зондов.

Еще одной задачей является обеспечение способа, дополнительно содержащего способ по п.1, дополнительно содержащий этап, на котором оценивают положение одного или нескольких зондов.

Еще одной задачей является обеспечение способа, дополнительно содержащего способ по п.1, дополнительно содержащий этап, на котором обрабатывают изображение путем прореживания или обрезки.

Еще одной задачей является обеспечение способа, дополнительно содержащего способ по п.1, дополнительно содержащий этап, на котором преобразуют данные изображения в меру биологической активности.

Эти и другие аспекты изобретения более подробно объяснены со ссылкой на следующие варианты осуществления и со ссылкой на фигуры.

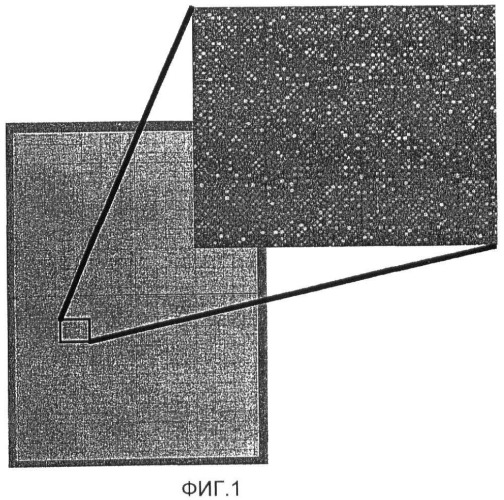
Фиг.1 - изображение ROMA с 85000 зондов, сканированное с разрешением 2 мкм (размер изображения равен 150 Мб).

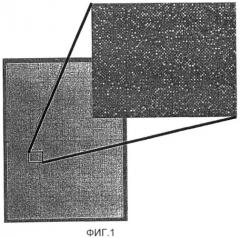
Фиг.2 - изображение системы координат программы.

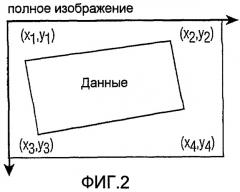
Фиг.3 - псевдокод для алгоритма Find_corners (изображения).

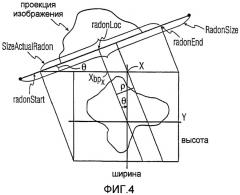
Фиг.4 - проекция пространства Радона в пространство изображения.

Фиг.5 - пример преобразования Радона для наилучшего угла.

Фиг.6 - пример БПФ проекции изображения.

Фиг.7 - пример преобразования Радона для изображения, имеющего опорные точки.

Фиг.8 - увеличение проекции с фиг.7.

Фиг.9 - оценочные линии в изображении ROMA.

В данном раскрытии представлен способ автоматического нахождения углов, а также привязки к сетке или нахождения внутренних зондов, изображений микроматрицы, который позволяет декодировать изображения в числа. Мы использовали методы обработки изображения, например преобразования Радона и быстрые преобразования Фурье, и несколько эвристик для нахождения точного положения углов и зондов микроматрицы. На основании нашей техники мы способны идентифицировать углы в пределах нескольких пикселей даже для схемы без зондов в углах.

Пример изображения микроматрицы высокой плотности (в нашем случае, изображения ROMA) показан на фиг.1. Существуют различные методы размещения конструкции зондов. Зонды, исследованные к настоящему времени, представляют собой квадраты со стороной 16 мкм с промежутками между ними 2 мкм. Изображения можно сканировать с разрешением 5 мкм, 2 мкм или 1 мкм, и даже возможно разрешение меньше микрона, в результате чего получаются изображения с 3, 8 или 16 пикселями на зонд и нулем, одним или двумя пикселями на промежуток.

Согласно раскрытому здесь способу, для чипов высокой плотности (т.е. 85000-400000 зондов) можно использовать эвристики: 1) прореживая изображения в горизонтальном и вертикальном направлениях (например, беря каждый второй пиксель или каждый четвертый пиксель). Кроме того, можно взять часть верхней левой четверти изображения и часть верхней правой четверти изображения, часть нижней левой и нижней правой, чтобы сделать разумный размер изображения, чтобы начать с первого приближения. Это также можно делать на основании печатного шаблона и опорных точек.

Кроме того, чипы печатаются с разнообразными шаблонами опорных точек (которые выглядят как очень яркие зонды). Каждое изображение сканируется на двух цветовых частотах (обычно флуорофоры Cy3 и Cy5). Наилучшие результаты обработки изображения для алгоритма нахождения углов ожидаются из анализа полных интенсивностей изображений, т.е. суммы двух цветовых частот. Автоматическое декодирование изображения микроматрицы необходимо для нахождения угловых точек, для осуществления привязки к сетке и декодирования в данные микроматрицы. В этом процессе алгоритмы интеллектуальной обработки изображения необходимы для очистки от артефактов, создаваемых химическими реакциями (т.е. нормализации) и процессом сканирования.

Задачей описанного ниже программного обеспечения является автоматическое определение положения четырех углов матрицы зондов в пиксельных координатах. На основании этой информации можно использовать билинейное преобразование для определения положения центров масс зондов без учета синусоидальных возмущений. Технология ROMA для матриц высокой плотности является новым подходом, и в настоящее время не существует адекватных методов обработки этих изображений.

Нахождение угловых точек в изображении микроматрицы является первым шагом, необходимым для осуществления привязки к сетке для нахождения положения зондов в изображении и декодирования в данные микроматрицы. Процесс формирования изображения привносит артефакты и перекашивает изображение. Важно обнаруживать и компенсировать артефакты, порождаемые процессом сканирования. Мы разработали многопроходный алгоритм обнаружения угловых точек в изображении микроматрицы высокого разрешения и высокой плотности. Алгоритм состоит из внешнего и внутреннего циклов. Внешний цикл делает первый проход при нахождении углов, которое является точным, при условии отсутствия трапецеидального искажения (т.е. матрица зондов сохраняет прямоугольную форму). Вычисляется метрика согласия, и, если она удовлетворительна, алгоритм выдает свои результаты и останавливается. Если эта проверка не проходит, выполняется внутренний цикл, который пытается скорректировать трапецеидальное искажение. Опять же, вычисляется метрика согласия, и, если она приемлема, возвращаются результаты, в противном случае алгоритм сообщает об ошибке и останавливается. Результаты представляют собой координаты x и y углов матрицы зондов в пикселях, как показано на фиг.2.

Алгоритм использует преобразование Радона. Преобразование Радона можно рассматривать как аналог наблюдения сада с разных углов. При наблюдении строго под прямым углом, все деревья и промежутки между рядами отчетливо видны. Если пиксели в изображении суммировать под этим углом, будут наблюдаться отчетливые и регулярные колебания интенсивности (см. фиг.7 и 8). Вычисляется преобразование Фурье преобразования Радона, и для идентификации оптимального угла используется эвристический критерий.

Эта эвристика применяется для получения наилучшего угла поворота в горизонтальном и вертикальном направлениях. После выбора оптимального угла поворота края матрицы зондов идентифицируются путем выбора первого и последнего локальных максимумов в преобразовании Радона для этого угла. Эта операция сначала осуществляется на всем изображении. Затем, если мера согласия указывает, что изображение имеет трапецеидальное искажение, весь процесс повторяется в горизонтальном и/или в вертикальном направлении, при этом субизображения обрезаются для проверки только непараллельных краев. Псевдокод алгоритма представлен на фиг.3.

Алгоритм нахождения линий (findLines) вдоль крайних правого и левого краев изображения выражается следующим образом.

Применяем преобразование Радона к входному изображению микроматрицы. Преобразование Радона проецирует изображение в пространство полярных координат, т.е. пространство углов и расстояний (θ и ρ), когда это возможно, для нахождения ориентации прямых линий.

,

где g(x,y) выражает исходное изображение как матрицу интенсивностей в декартовых координатах, выражает изображение, подвергнутое преобразованию Радона, θ - угол поворота, и ρ - наименьшее расстояние до начала отсчета системы координат, и δ( ) - дельта-функция Дирака.

Для минимизации вычислительных затрат алгоритм осуществляет иерархическое преобразование Радона начиная с изменения θ от -1 до +1 градусов с шагом в 0,1 градуса. Наш опыт с изображениями из одного сканера говорит о том, что этот диапазон адекватен для этого сканера. Другой сканер с большим углом поворота может потребовать расширения этого диапазона. Преобразование Радона последовательно применяется для всех θ ∈ {-1, -0,9, -0,8, ..., 1}. На фиг.5 показан пример проекции преобразования Радона для конкретного θ.

Применяем быстрое преобразование Фурье к каждой из θ-кривых для нахождения угла наклона изображения. Выбирается угол наклона θ _k, БПФ которого содержит наибольшую энергию на одной частоте. На фиг.6 показано БПФ проекции, показанной на фиг.5.

На этот раз берем θ _k и применяем преобразование Радона от θ _k-0,1 до θ _k+0,1 с величиной шага 0,01 и переходим к этапу 3. Опять же, эти варианты выбора параметров могут разниться для разных наборов сканер-изображение. Для каждого применения преобразования Радона с конкретным значением θ получаем вертикальную проекцию изображения в пространство ρ. Для каждого тета (θ ₁, …, θ ₂₁) получаем отдельную кривую, из которой выбирается кривая, которая имеет наибольшую энергию на одной частоте в своем быстром преобразовании Фурье, в качестве наилучшего угла поворота.

Находим локальные максимумы преобразования Радона наилучшего угла. На фиг.7 показано преобразование Радона для угла, который имеет наибольшую энергию на одной частоте. Звездочки обозначают локальные максимумы.

Находим первый и последний локальные максимумы, которые составляют, по меньшей мере, 20% от глобального максимума. Малые кружки в начале и конце графика на фиг.7 обозначают выбранные первый и последний локальные максимумы. Альтернативно, если найден пик, значительно превышающий средний уровень сигнала, считаем его нашим первым/последним локальным максимумом и игнорируем другие пики вокруг этих максимумов (фиг.7). Это обычно имеет место для конструкций, где опорные точки окружают зонды. Увеличение проекции и выбранных локальных максимумов показано на фиг.8. Первый и последний столбец оцениваются по первому и последнему локальным максимумам, которые отвечают определенным критериям. Это необходимо для отсечения шума измерения до фактического начала матрицы изображения. Для осуществления этой обработки рассматриваем только максимумы в первой и последней третях изображения. Берем подмножество локальных максимумов, локальный средний градиент которых меньше 20%. Затем находим первый максимум, высота которого составляет, по меньшей мере, 25% средней интенсивности в средней трети изображения. Это позволяет захватить края типичной матрицы. Затем, в случае наличия опорных точек проверяем, действительно ли максимальное значение в первой (или последней) трети вдвое больше среднего значения первой (или последней) трети изображения. Если мы получаем такие точки, мы обозначаем их как первый и последний значимые максимумы вместо найденных ранее. Малые кружки в начале и конце на фиг.7 обозначают выбранные первый и последний локальные максимумы. Увеличение проекции и выбранных локальных максимумов показано на фиг.8.

Выполняем обратную проекцию соответствующих первого и последнего локальных максимумов в пространство изображения для нахождения, в первом приближении, линий, проходящих через первый и последний столбцы изображения. При этом линии задаются углами и точками, найденными из обратной проекции. Это линии, проходящие через самый левый и самый правый столбцы. Следующее уравнение отображает ρ в пространстве Радона в пространство изображения. На фиг.4 графически представлено оценивание, которое необходимо осуществлять.

.

Каждое преобразование Радона имеет длину RadonSize, которая является максимально возможным размером преобразования Радона. Она задана следующим уравнением:

.

Преобразование Радона для всех остальных углов покрывает лишь часть матрицы размера RadonSize. Оно задано следующим уравнением:

Для каждой нужной точки в преобразовании Радона ее обратная проекция в пространство изображения задается как

Нужно получить уравнение линии, которая проходит через эту точку в изображении.

Угол наклона задается углом тета, который выбран как имеющий наибольшее значение на одной частоте после осуществления быстрого преобразования Фурье (БПФ). Чтобы оценить значение константы c в уравнении, имеем y = 0 для обратно спроецированной точки преобразования Радона. Поэтому

Затем осуществляем этапы 2-7 для повернутого изображения для оценивания линий, проходящих через верхнюю и нижнюю строки.

Для нахождения первого приближения углов находим пересечение четырех линий (верхней, нижней, левой и правой). Из вышеописанных этапов имеем уравнения четырех линий и решаем четыре уравнения для оценивания четырех угловых точек.

Затем проверяем согласие оценочных углов. С этой целью снова используем преобразование Радона. Для БПФ преобразования Радона для выбранного тета (θ _i) вычисляем отношение (r _i) глобального максимума к суммарной энергии вокруг глобального максимума частоты энергии, которая вычисляется следующим образом:

[maxEnergy i]=max(fft)

maxEnergySum=sum(fft(i-10:i+10))

r _i=maxEnergySum/maxEnergy.

Если это отношение r _i ниже выбранного порога (выбранного равным 0,4 эвристически на основании ряда экспериментов и оценивающего, что хорошо работает), обрезаем изображение вокруг первого приближения и повторно применяем преобразование Радона. Вышеописанный процесс повторяется, и даже если во втором раунде это отношение оказывается ниже выбранного порога, возвращается неудача.

Мы использовали пробные изображения переменного разрешения для испытания нашего алгоритма. Различные пробные изображения и их разрешения представлены в таблице 1. Во многих случаях Cy5 и Cy3 представляли собой два изображения, объединенные в одном файле tiff. Всего было протестировано четырнадцать изображений.

Таблица 1Пробные изображения и их разрешение
Разрешение сканирования	Количество изображений	Номера изображений
5 мкм	9	1-9
2 мкм	2+2*	10-11
1 мкм	1	12

В таблице 2 представлено положение «на месте» углов для двенадцати из четырнадцати изображений, указанных в таблице 1. Два изображения, обозначенные как 2* в таблице 1, просканированные с разрешением 2 мкм, не рассматривались для последующего вычисления, поскольку алгоритм возвратил неудачу. Изображения были размытыми, и алгоритм не смог хорошо оценить угол поворота, на этапе 9 была объявлена неудача после осуществления преобразования Радона на обрезанных изображениях. Ситуация «на месте» оценивалась вручную путем наблюдения изображений в фигуре MATLAB и установления центра на верхнем правом зонде. В случае отсутствия зонда проводили линии и определяли угловую точку как точку пересечения этих линий. Для изображения 11 гибридизация чипа ROMA работала неудовлетворительно, и углы были размытыми, что не позволяло оценивать их вручную (в таблице отмечено словом «нет»). В таких случаях автоматизированный способ чрезвычайно полезен, поскольку оператор-человек не способен находить углы. Ситуацию «на месте» для изображения 11, для точности вычисления, взяли такую же, как для изображения 10, которое было просканировано для флуорофора Cy3.

Таблица 2Положение углов «на месте» для двенадцати изображений
Углы «на месте»	x1	x2	x3	x4	y1	y2	y3	y4
1	105	80	2690	2665	50	3504	64,1	3519
2	91,5	94	2677	2679	87	3541	83	3536,5
3	91	93,5	2676,5	2679	86	3540	81	3534,5
4	70	74	2655	2659,5	46	3500	39,5	3493,5
5	70	74,5	2655	2659,5	46	3500	39,5	3493
6	86,4	89,4	2668,7	2672,6	110,4	3563,6	104	3557,6
7	79,4	82,5	2664,6	2666,6	152,3	3605,4	147,4	3601,4
8	58,5	61,5	2643,5	2646,5	114	3567,5	108,5	3562
9	73,5	75,5	2656,5	2658,5	53,5	3506,5	51	3504,5
10	421	398	7241	7215	263	8657	200	8592
11	Нет	Нет	7241	7216,5	Нет	Нет	200	8593
12	1017,5	982	14244	14206	511,5	17568	377	17432

В таблице 3 представлены оценочные углы и полная абсолютная разность (TAD) между оценочными значениями углов, полученных с помощью алгоритма, и значениями, полученными «на месте», приведенными в таблице 2, для каждого изображения. Например, для изображения 1, TAD в таблице 3 вычисляется как сумма абсолютных разностей для x₁ в таблицах 2 и 3 (т.е. 105,3-105=0,3); x₂ (т.е. 80-80=0); x₃ (2690,3-2690=0,3); x₄ (2665-2665=0); y₁ (50,4-50=0,4); у₂ (3504,4-3504=0,4); y₃ (64,6-64,1=0,5) и y₄ (3519,5-3519=0,5). Поэтому, суммируя абсолютные разности, получаем для изображения 1 TAD, равную 2,4. На фиг.9 показан пример оценочных линий и углов в изображении ROMA. Это визуальный выход программы, где можно видеть оценочные линии и углы в наложении на фактическую матрицу ROMA.

Таблица 3Оценочное положение углов совместно с полной абсолютной разностью относительно положения «на месте» для углов всего изображения
Оценочные углы	x1	x2	x3	x4	y1	y2	y3	y4	Полная абсолютная разность (TAD)
1	105,3	80	2690,3	2665	50,4	3504,4	64,6	3519,5	2,4
2	92,1	94,8	2677,1	2679,8	86,6	3540,6	82,3	3536,3	4
3	92,1	94,8	2677,1	2679,8	85,9	3539,9	81,1	3535,1	4,7
4	70,5	74,4	2656,5	2660,4	46,1	3500,1	40,9	3494,9	6,3
5	70,5	74,4	2655,5	2659,4	46,6	3499,6	40,5	3493,5	3,7
6	86,4	90,6	2669,4	2673,6	111,8	3564,8	105,2	3558,2	7,3
7	80,2	82,9	2665,2	2667,9	152,9	3606,9	148,2	3602,2	6,8
8	59	62	2644	2647	113,5	3567,5	108,5	3562,5	3
9	74,3	76,7	2657,3	2659,7	52,9	3505,9	51,1	3504,1	5,7
10	421,3	397,9	7239,5	7216,1	265,5	8658,1	200	8592,6	7,2
11	421,3	397,9	7239,5	7216,1	265,5	8658,1	200	8592,6	2,3
12	1010,4	992,5	14238	14220	512,9	17568	377,8	17433	5,45

В таблице 4 показано значение разности в расчете на оценочный пиксель (DPEP), а также значение как процент от размера зонда. Это сумма всех абсолютных разностей при каждом из разных разрешений сканирования, деленная на количество изображений, умноженное на восемь (мы оценивали восемь значений для каждого изображения). Каждый зонд имеет форму квадрата со стороной 16 мкм. Таким образом, при 5 мкм существует примерно 3×3 пикселей на зонд и т.д.

DPEP=∑ TAD/(полное количество изображений · 8)

Таблица 4Абсолютная разность в расчете на оценочное значение, выраженная в процентах от размера зонда
Разрешение сканирования	Разность в расчете на оценочный пиксель	Пикселей на зонд(ширина 16 мкм)	Процент от размера зонда
5 мкм	0,609722	3×3	20,32407
2 мкм	0,59375	8×8	7,421875
1 мкм	1,3625	16×16	8,515625

Таким образом, используя преобразование Радона, можно точно оценить углы изображения ROMA высокой плотности. В данном наборе данных максимальная разность составляет около 20% размера зонда. Это означает, что для нахождения наилучшей сетки привязки область поиска вокруг оценочного угла должна составлять, самое большее, порядка нескольких пикселей. Это избавляет от необходимости вмешательства человека для нахождения точек сетки изображения, обеспечивая широкую область применения этой технологии. Раскрытый здесь способ, отвечающий изобретению, дает большие возможности автоматизации всего процесса преобразования изображений ROMA высокого разрешения в числа.

Помимо применения к ROMA, также предполагается, что раскрытый способ можно использовать для других типов матриц, в том числе матриц экспрессии генов, матриц для анализа однонуклеотидного полиморфизма (SNP), матриц ЦГ-богатых островков, микроматриц промоторов, матриц взаимодействия белок-ДНК и др., включая микроматрицы, имеющие «пустые» зонды в углах, которые очень трудно оценить вручную. Кроме того, с помощью быстрого преобразования Фурье в совокупности с преобразованием Радона можно обнаруживать синусоидальную волну, которая может иметь место, когда сканер работает в режиме высокого разрешения. Дополнительно, мы полагаем, что расширение нашего алгоритма позволит практически удвоить емкость микроматриц и использовать все пространство чипа, а не шаблон в виде шахматной доски, который используется в настоящее время, чтобы зонды можно было правильно считывать.

Аналогично вышеописанному способу, где проекции Радона осуществлялись только для прямых линий, для компенсации синусоидального изменения изображение можно проецировать вдоль синусоид с разными частотами, с разными фазами и разными амплитудами для нахождения наиболее подходящих синусоиды и угла поворота. Этот способ позволит компенсировать синусоидальное изменение и определять положение зонда с более высокой точностью. Такая проекция может быть необходима для нахождения локальных минимумов преобразования Радона, которое выбрано, и для определения, находится ли сумма минимумов в пределах порога. В случае отсутствия синусоидального изменения минимумы будут близки к нулю. В противном случае будет существовать значение, немного превышающее фоновый шум, которое может инициировать осуществление этого этапа компенсации синусоидального изменения.

Для оценивания зондов мы находим локальные максимумы преобразования Радона для наилучших угла, частоты, фазы и амплитуды и проецируем их обратно в пространство изображения в горизонтальном и вертикальном направлениях. Пересечения этих линий дают положение зондов.

Также предполагается, что раскрытый способ можно использовать для: 1) обработки изображения путем прореживания или обрезки для повышения скорости обработки - это может играть важную роль при более высоких плотностях или для пакетной обработки; 2) обработки декодирования в данные. Одна возможность состоит в декодировании обрезанной матрицы в пространственной области. Это также можно производить на основании данных преобразования Фурье.

Хотя настоящее изобретение описано в отношении конкретных вариантов его осуществления, специалисты в данной области техники смогут предложить многочисленные модификации, расширения и/или изменения, не выходящие за рамки сущности и объема изобретения. Поэтому мы заявляем, что изобретение ограничивается только объемом формулы изобретения и ее эквивалентов.

1. Способ автоматической идентификации углов и зондов чипа микроматрицы в сканированном изображении микроматрицы высокой плотности и высокого разрешения, имеющем пространство изображения, содержащий этапы, на которых(a) применяют преобразование Радона к входному изображению микроматрицы для проецирования изображения в пространство углов и расстояний, когда это возможно, для нахождения ориентации прямых линий,(b) применяют быстрое преобразование Фурье к спроецированному изображению, полученному на этапе (а), и применяют эвристику для нахождения оптимального угла наклона спроецированного изображения,(c) применяют эвристику для определения оптимальных первого и последнего локальных максимумов для оптимального угла наклона,(d) выполняют обратную проекцию определенных первого и последнего локальных максимумов в пространство изображения для нахождения, в первом приближении, первой и последней вертикальных линий изображения,(e) поворачивают изображение и повторяют этапы (a)-(d) для нахождения, в первом приближении, верхней и нижней горизонтальных линий изображения,(f) определяют, в первом приближении, четыре угла изображения из пересечения вертикальных и горизонтальных линий,(g) применяют эвристику для определения того, достаточно ли первого приближения, полученного на этапе (f), и,(h) опционально, обрезают сканированное изображение вокруг первого приближения четырех углов и повторяют этапы (a)-(f).

2. Способ по п.1, в котором сканированное изображение микроматрицы представляет собой изображение, полученное посредством элемента, выбранного из группы, состоящей из репрезентативного анализа олигонуклеотидной микроматрицы, матриц экспрессии генов, матриц однонуклеотидного полиморфизма, матриц ЦГ-богатых островков, микроматриц промоторов и матриц взаимодействия белок-ДНК.

3. Способ по п.1, в котором ошибочные искажения в изображении включают в себя эффекты трапецеидального искажения.

4. Способ по п.1, в котором ошибочные искажения в изображении включают в себя синусоидальные или искривленные линии размещения зондов вместо прямых линий размещения.

5. Способ по п.1, в котором разрешение сканированного изображения составляет 1, 2 или 5 мкм.

6. Способ по п.1, в котором сканированное изображение сканируют с использованием флуорофоров Су3 и Су5.

7. Способ по п.1, в котором сканированное изображение получают из чипа, содержащего от около 85000 зондов до около 400000 зондов.

8. Способ по п.1, дополнительно содержащий этап, на котором оценивают положение одного или нескольких зондов.

9. Способ по п.1, дополнительно содержащий этап, на котором обрабатывают изображение путем прореживания или обрезки.

10. Способ по п.1, дополнительно содержащий этап, на котором преобразуют данные изображения в меру биологической активности.