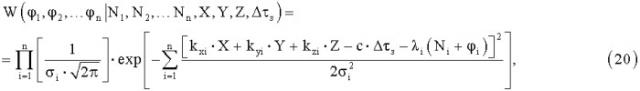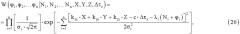Способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем

Способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области спутниковой навигации и может быть использовано для определения углового положения объектов в пространстве или на плоскости.

Известен способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем [1], основанный на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата, в котором в течение интервала времени измерения проводят m измерений фазовых сдвигов между парами антенно-приемных устройств, а текущее угловое положение объекта определяют путем решения следующей системы уравнений:

,

где i=1,…,n - текущий номер космического аппарата;

j=1,…,m - номер измерения фазовых сдвигов сигналов n космических аппаратов;

n - общее число принимаемых космических аппаратов;

m - общее число измерений фазовых сдвигов сигналов n космических аппаратов;

k_xij, k_yij, k_zij - направляющие косинусы векторов-направлений от объекта до i-го космического аппарата в j-й момент времени;

ψ_ij - значение фазового сдвига сигнала i-го космического аппарата в j-й момент времени;

X_j, Y_j, Z_j - значения направляющих косинусов в j-й момент времени;

λ_i - длина волны i-го космического аппарата;

ΔS_i - систематическая погрешность измерения фазового сдвига сигнала i-го космического аппарата, складывающаяся из целочисленной неоднозначности и аппаратурной составляющей систематической погрешности.

Недостатком способа является необходимость проведения m разновременных измерений фазовых сдвигов между разнесенными антеннами объекта, что увеличивает время, требуемое для определения угловой ориентации. Кроме того, точность определения угловой ориентации объекта зависит от величины поворота антенной системы объекта и величины изменения углового положения принимаемых космических аппаратов относительно вектора-базы, образованного разнесенными антеннами объекта. При этом, если антенная система объекта будет малоподвижной в течение времени измерения, то время, необходимое для получения заданной точности оценки углового положения, может составлять единицы - десятки минут.

Известен способ угловой ориентации объекта по сигналам спутниковых радионавигационных систем [2], взятый в качестве прототипа, основанный на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на разнесенные две или более антенны, расположенные параллельно одной или двум осям измеряемого объекта, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата, проведении в течение интервала времени измерения m измерений фазовых сдвигов между парами антенно-приемных устройств, в котором осуществляют подбор значений целочисленных неоднозначностей измерений фазовых сдвигов для минимального созвездия из s космических аппаратов, позволяющий определить возможные значения угловой ориентации, отбор возможных значений угловой ориентации по заранее известным значениям ориентации антенной системы и расстояния между разнесенными антеннами, проверку оставшихся значений угловой ориентации расчетом значений неоднозначности Nj для измеренных фазовых сдвигов дополнительных космических аппаратов, не вошедших в начальное созвездие, решение системы уравнений для определения угловой ориентации по измеренным значениям фазовых сдвигов сигналов всех принимаемых космических аппаратов, при этом значение, соответствующее искомой угловой ориентации объекта, определяется из условия максимума функции правдоподобия, а возможные значения угловой ориентации определяются путем решения системы уравнений, составленной по измерениям фазовых сдвигов для минимального созвездия из s космических аппаратов, имеющей вид:

,

где i=1,…,s - текущий номер космического аппарата из числа входящих в начальное созвездие;

s=2, 3 - общее число КА, вошедших в начальное созвездие;

k_xi, k_yi, k_zi - направляющие косинусы векторов-направлений от объекта до i-го космического аппарата в текущий момент времени измерений;

ψ_i - измеренное и скорректированное с учетом систематической погрешности значение фазового сдвига сигнала i-го космического аппарата;

λ_i - длина волны сигнала i-го космического аппарата;

N_i - значение целочисленной неоднозначности сигнала i-го космического аппарата, удовлетворяющее условию: ;

В - значение расстояния между антеннами, при s=2 - известное с высокой точностью, при s=3 - подлежащее уточнению в процессе решения системы уравнений;

X, Y, Z - неизвестные значения относительных координат фазового центра второй антенны относительно первой.

Недостатком этого способа является то, что для его реализации требуется предварительная коррекция измеренных фазовых сдвигов на величину аппаратурной составляющей систематической погрешности, вызванной неодинаковыми значениями группового времени запаздывания (ГВЗ) сигналов в антенно-приемных устройствах (далее антенно-приемные каналы), являющихся составной частью устройства определения угловой ориентации, размещаемого на объекте. Устройство определения угловой ориентации является одним из возможных вариантов реализации аппаратуры потребителей (АП) спутниковых радионавигационных систем.

При неодинаковых значениях ГВЗ в антенно-приемных каналах разность значений ГВЗ в них будет отличаться от нуля. Если в расчетах принять указанную разность значений ГВЗ равной нулю, то это приведет к снижению точности оценки угловой ориентации объекта.

В основу изобретения положена задача повышения точности определения угловой ориентации на основе расчета разности ГВЗ в антенно-приемных каналах как дополнительного неизвестного параметра при оценке угловой ориентации объекта.

Поставленная задача решается тем, что в способе угловой ориентации объекта, по сигналам спутниковых радионавигационных систем, основанном на приеме сигналов от космических аппаратов глобальных навигационных спутниковых систем на расположенные параллельно одной или двум осям измеряемого объекта разнесенные две или более антенны антенно-приемных каналов, измерении фазового сдвига между принятыми сигналами от каждого космического аппарата, проведении в течение интервала времени измерения m измерений фазовых сдвигов принятых сигналов между парами антенно-приемных каналов, подборе значений целочисленных неоднозначностей для минимального созвездия из s космических аппаратов, позволяющем определить возможные значения угловой ориентации, отборе возможных значений угловой ориентации по заранее известным значениям ориентации антенной системы и расстояний между разнесенными антеннами, проверке оставшихся значений угловой ориентации расчетом значений неоднозначности N_i для измеренных фазовых сдвигов дополнительных космических аппаратов, не вошедших в начальное созвездие, определении угловой ориентации объекта по измеренным значениям фазовых сдвигов сигналов всех принимаемых космических аппаратов, определении значения искомой угловой ориентации объекта по максимуму функции правдоподобия, согласно изобретению возможные значения угловой ориентации определяют решением системы уравнений, составленной по измерениям фазовых сдвигов для минимального созвездия из s космических аппаратов, имеющей вид:

,

где i=1,…,s - текущий номер космического аппарата из числа входящих в начальное созвездие;

s=3 или s=4 - общее число КА, вошедших в начальное созвездие;

с - скорость распространения радиосигналов, равная скорости света в вакууме;

k_xi, k_yi, k_zi - направляющие косинусы векторов-направлений от объекта до i-го космического аппарата в текущий момент времени измерений;

φ_i - измеренное значение фазового сдвига сигнала i-го космического аппарата, выраженное в фазовых циклах;

λ_i - длина волны сигнала i-го космического аппарата;

N_i - целочисленная неоднозначность сигнала i-го космического аппарата, удовлетворяющая условию:

В - расстояние между антеннами, при s=3 - известное с высокой точностью, при s=4 - подлежащее уточнению в процессе решения системы уравнений;

X, Y, Z - неизвестные значения относительных координат фазового центра второй антенны относительно первой;

Δτ_з - разность группового времени запаздывания в антенно-приемных каналах устройства определения угловой ориентации при условии, что

,

где Δτ_з - априорное значение разности группового времени запаздывания в антенно-приемных каналах, заданное при изготовлении или начальной калибровке устройства;

Δτ_доп - максимально допустимое отклонение между полученной разностью группового времени запаздывания Δτ_з и ее априорным значением.

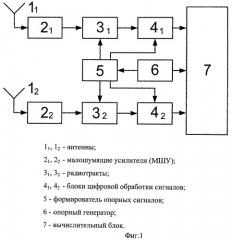
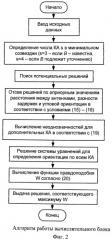
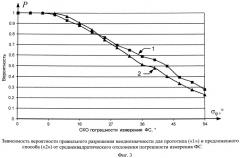
Изобретение поясняется прилагаемыми чертежами, в которых на фиг.1 изображена структурная схема размещаемого на объекте устройства определения угловой ориентации, реализующего предложенный способ, на фиг.2 изображена блок-схема алгоритма работы вычислительного блока, реализующего алгоритм определения угловой ориентации в соответствии с предлагаемым способом, на фиг.3 приведены результаты расчета вероятности правильного разрешения неоднозначности для прототипа и предлагаемого способа определения угловой ориентации.

Сущность предлагаемого способа можно пояснить следующим образом. При определении угловой ориентации объектов интерферометрическим методом по сигналам спутниковых радионавигационных систем (СРНС) используют результаты измерений косинусов углов α_i между вектором-базой, образованном приемными антеннами и вектором-направлением на i-й космический аппарат (КА) СРНС.

Фазовый сдвиг (ФС) сигнала i-го КА, принимаемого двумя пространственно разнесенными антеннами, и косинус угла между вектором-базой и вектором-направлением на КА связаны между собой выражением:

где i=1,…,n - текущий принимаемый сигнал КА;

n - общее число КА, используемых для определения угловой ориентации объекта;

λ_i - длина волны сигнала i-го КА;

Ф_i - полный фазовый сдвиг сигналов i-го КА, принятых разнесенными антеннами объекта, выраженный в фазовых циклах (1 фазовый цикл соответствует фазовому сдвигу 2π радиан или 360°);

В - расстояние между пространственно разнесенными антеннами АП.

Вычисление направляющих косинусов вектора-базы можно осуществить на основе уравнения, полученного исходя из свойства скалярного произведения векторов в декартовой системе координат:

где cosβ_x, cosβ_y, cosβ_z - неизвестные направляющие косинусы вектора-базы объекта;

k_xi, k_yi, k_zi - направляющие косинусы векторов - направлений между объектом и i-м КА.

Значения направляющих косинусов зависят от координат КА и объекта и определяются в соответствии с выражениями:

где x, y, z - известные координаты объекта в геоцентрической системе координат (ГЦСК);

x_ci, y_ci, z_ci - координаты i-го КА в ГЦСК, полученные из решения задачи размножения эфемерид КА;

- расстояние между объектом и i-м КА, полученное на основе известных координат объекта и i-го КА.

Систему уравнений (2) можно дополнить нелинейным уравнением связи между направляющими косинусами вектора-базы:

При определении углового положения объекта часто неизвестными являются не только направляющие косинусы вектора-базы, но и сама величина базы В. В связи с этим выражения (2) и (4) запишутся следующим образом:

где X=B·cosβ_x;

Y=B·cosβ_y;

Z=B·cosβ_z.

Величины X, Y, Z являются геоцентрическими координатами фазового центра второй антенны относительно фазового центра первой антенны, взятой в качестве опорной. При определении угловой ориентации с целью повышения точности используется расстояние между антеннами В, значительно превышающее длину волны принимаемых сигналов λ. Кроме того, вследствие разброса электрических характеристик антенн, антенных кабелей, блоков усиления и преобразования частоты в каналах основной и вспомогательной антенн интерферометра (антенно-приемных каналах), при измерениях ФС возникают аппаратурные систематические погрешности, обусловленные разностью ГВЗ сигналов.

Исходя из этого выражение для полного фазового сдвига сигнала i-го КА, принятого разнесенными антеннами объекта, примет вид:

где N_i - целое число фазовых циклов неоднозначности в полном ФС сигнала i-го КА (далее именуемое неоднозначностью);

Δφ_ci - аппаратурная систематическая погрешность измерения ФС сигнала i-го КА, выраженная в фазовых циклах;

φ_i - измеренный ФС сигнала i-го КА, принятого двумя антеннами объекта, выраженный в фазовых циклах.

С учетом наличия систематической погрешности и неоднозначности в измеренных значениях ФС система уравнений (5) принимает вид:

Значения систематических погрешностей измеренных ФС КА Δφ_ci необходимо определять и исключать из результатов измерений до выполнения решения задачи определения угловой ориентации.

Пренебрежение величинами Δφ_ci приводит к увеличению погрешности определения неизвестных параметров X, Y, Z и снижению точности определения угловой ориентации.

Для повышения точности определения угловой ориентации при наличии систематической погрешности измерения фазовых сдвигов требуется ввести данную составляющую погрешности в число оцениваемых параметров системы уравнений (7), что достигается переносом величины, содержащей Δφ_ci, в левую часть системы и приведением (7) к следующему виду:

Значение произведения λ_i·Δφ_ci может быть представлено в виде:

где с - скорость распространения радиосигналов;

f_i - рабочая частота сигнала i-го КА, принимаемого аппаратурой потребителей;

Δτ_з - разность ГВЗ в антенно-приемных каналах, возникающая вследствие разброса электрических характеристик антенн, антенных кабелей, блоков усиления и преобразования частоты принимаемых сигналов в антенно-приемных каналах АП.

Значение разности ГВЗ Δτ_з считается не зависящим от частоты принимаемых сигналов в диапазоне рабочих частот спутниковых радионавигационных систем (СРНС), что основано на следующем. Полоса частот антенн, антенных кабелей и малошумящих усилителей (МШУ) значительно превосходит полосу рабочих частот используемых СРНС, что приводит к высокой линейности их фазочастотных характеристик в указанном диапазоне, следовательно, к постоянству их производных, представляющих собой значения группового времени запаздывания сигналов в антенно-приемных каналах АП. При создании АП СРНС, выполняющей интерферометрические измерения, перед разработчиками ставится задача максимального уменьшения как значения Δτ_з, так и ее зависимости от

частоты принимаемых сигналов. Это достигается размещением антенн АП на единой антенной платформе, с выравниванием электрических параметров соединительных кабелей и характеристик цепей предварительного усиления сигналов. Помимо этого принимаются схемотехнические решения, направленные как на максимальное использование цифровой обработки сигналов в тракте приема и обработки сигналов СРНС, так и на обеспечение равенства ГВЗ в аналоговых частях разных антенно-приемных каналов.

Указанные меры обеспечивают минимизацию разности ГВЗ и уменьшение ее неравномерности в диапазоне частот КА СРНС, принимаемых АП. Исходя из условия постоянства разности ГВЗ Δτ_з в антенно-приемных каналах система уравнений (8) запишется следующим образом:

Система уравнений (10) содержит n+5 неизвестных, в число которых входят n неоднозначностей N_i (i=1,…,n), 3 направляющих косинуса вектора-базы X, Y, Z, разность ГВЗ Δτ_з и расстояние между антеннами В. Число уравнений системы (10) складывается из n линейных и одного нелинейного уравнения связи между величинами X, Y, Z и В и равно n+1. Поскольку число неизвестных превышает число уравнений, система (10) является вырожденной и не может быть решена на практике.

Для обеспечения решения системы уравнений (10) используют свойство целочисленности неоднозначностей измерения ФС N₁,…,N_n. Диапазон возможных значений целочисленных неоднозначностей определяется максимально возможным числом длин волн принимаемых сигналов, укладывающихся на расстоянии В между антеннами объекта, что соответствует случаю совпадения направления вектора-базы с направлением на данный КА. Таким образом, для нахождения угловой ориентации с использованием системы уравнений (10) требуется осуществить перебор значений целочисленной неоднозначности N_i для каждого из принимаемых

КА в диапазоне:

где int(.) - означает операцию выделения целой части числа, заключенного в скобки;

В - расстояние между антеннами;

λ_i - длина волны сигнала i-го КА;

φ_i - измеренное значение ФС сигнала i-го КА.

Например, при расстоянии между антеннами B=0.7 м, если в первом приближении принять значения измеренных фазовых сдвигов φ_i=0, диапазон перебираемых неоднозначностей N_i будет находиться в пределах -4≤N_i≤4, т.е. неоднозначность по каждому из спутников N_i будет соответствовать одному числу из ряда: -4, -3, -2, -1, 0, 1, 2, 3, 4. Значения неоднозначностей N_i ФС принимаемых КА могут наблюдаться во всех возможных сочетаниях.

Число возможных сочетаний неоднозначностей N_max для работы по сигналам n КА составляет:

Таким образом, для определения угловой ориентации требуется многократное решение системы уравнений (10) при заданных в каждом случае значениях вектора неоднозначностей NN=(N₁,N₂,…,N_n)^T, в котором каждый из элементов N_i вектора NN должен удовлетворять условию (11). Поскольку значения вектора NN подвергаются перебору, они полагаются известными при решении системы уравнений (10). Поэтому, если число принимаемых КА n оказывается больше или равно 4 (n≥4), система уравнений (10) не будет вырожденной и позволит определить неизвестные относительные координаты второй антенны объекта X, Y, Z, разность ГВЗ в антенно-приемных каналах Δτ_з и расстояние между антеннами В. Так как число возможных состояний вектора неоднозначности NN равно N_max (12), то в результате решения системы (10) будет получено N_max различных значений X, Y, Z, Δτ_з, B (далее будут называться потенциальными решениями).

При приеме сигналов СРНС ГЛОНАСС и GPS общее число КА n может составлять 16 и более. Исходя из этого, например, в рассмотренном примере при расстоянии между антеннами интерферометра B=0.7 м общее число потенциальных решений N_max составляет 9¹⁶≈1.8·10¹⁵.

В связи с этим прямое решение системы (10) путем перебора всех возможных состояний вектора неоднозначностей NN=(N₁,N₂,…,N_n)^T при большом числе принимаемых сигналов КА n требует очень больших вычислительных и временных затрат, и не может быть реализовано в реальных устройствах измерения угловой ориентации по сигналам СРНС. Число потенциальных решений N_max может быть уменьшено при переходе к системе нормальных уравнений (10), в которой число неизвестных равно числу уравнений и составляет 4. Для решения системы нормальных уравнений (10) достаточно принять на разнесенные антенны и измерить ФС сигналов 4-х КА, а определение неизвестных параметров будет базироваться на решении системы (10) при числе НКА s=4:

где i=1,…,s - текущий номер принимаемого КА.

В данной системе уравнений имеется 5 уравнений, 4 из которых линейны и составлены для измерений ФС 4-х КА, пятое уравнение нелинейно и не зависит от ФС сигналов КА. Число неизвестных в данной системе также равно пяти (неизвестны значения X, Y, Z, Δτ_з и В), т.е. система может быть решена однозначно. Решение системы (13) может осуществляться в два этапа: вначале определяют неизвестные значения X, Y, Z, Δτ_з из линейных уравнений, а затем, используя нелинейное уравнение, определяют значение расстояния между антеннами В.

Для рассмотренного выше примера определения угловой ориентации при расстоянии между антеннами В=0.7 м число перебираемых неоднозначностей составляет 9⁴=6561.

В случае, когда при определении угловой ориентации расстояние между антеннами В является известной величиной, число КА в минимальном созвездии может быть уменьшено до трех (s=3), т.е. система (13) запишется в виде:

В полученной системе неизвестными являются значения X, Y, Z, Δτ_з и для ее решения достаточно выполнить измерения ФС по сигналам трех КА. При этом число перебираемых неоднозначностей уменьшится и при расстоянии между антеннами В=0.7 м составит 9³=729.

Независимо от используемой для определения угловой ориентации системы уравнений, после перебора неоднозначностей и решения системы по минимальному созвездию из s КА (s=3 или s=4) образуется набор из

потенциальных решений, каждое из которых характеризует возможное угловое положение объекта и разность ГВЗ в антенно-приемных каналах АП. В данных потенциальных решениях содержатся:

- целочисленные неоднозначности измеренных значений ФС - N₁,…,N_s, где s - число КА, находящихся в минимальном созвездии;

- относительные координаты второй антенны - X, Y, Z, найденные в результате решения соответствующей системы уравнений;

- полученная разность ГВЗ в антенно-приемных каналах Δτ_з;

- уточненное расстояние В между антеннами объекта (при s=4).

Из полученного набора N_{max s} потенциальных решений требуется выбрать одно значение, которое с максимальной вероятностью соответствует искомому угловому положению объекта.

Для исключения избыточных потенциальных решений могут быть приняты следующие меры.

В системе уравнений (13), где происходит определение расстояния между антеннами (при s=4) организуется проверка полученных потенциальных решений по значению расстояния между антеннами

.

Условием исключения потенциальных решений является превышение некоторого заданного порогового значения ΔB_доп между полученным значением В и априорно известным расстоянием В_апр.

Следовательно, потенциальные решения, удовлетворяющие условию (15), исключаются из числа возможных значений угловой ориентации.

Дополнительным условием проверки является отличие полученной разности ГВЗ Δτ_з от своего априорного значения Δτ_апр на величину Δτ_доп, т.е. исключению из потенциальных решений подлежат те решения, которые не удовлетворяют условию:

Следует отметить, что при высокой технологичности изготовления интерферометрической АП СРНС можно принять значения Δτ_апр=0, а , где f - среднее значение частоты принимаемых сигналов.

Следующим критерием проверки является соответствие полученной ориентации максимально допустимому для данного объекта углу места вектора-базы. По известным формулам пересчета [3] относительные координаты второй антенны X, Y, Z переводятся в направляющие косинусы вектора - базы объекта cosβ_x, cosβ_y, cosβ_z, заданные в геоцентрической системе координат. Из полученных значений cosβ_x, cosβ_y, cosβ_z, используя известные формулы пересчета [3], можно перейти к направляющим косинусам в связанной с объектом системе координат cosβ_xt, cosβ_yt, cosβ_zt, а от них - к угловой ориентации вектора-базы в местной системе координат, заданной азимутом Ψ_а и углом места Ψ_ум.

По результатам сравнения полученного угла места Ψ_yм с его допустимым значением Ψ_{ум доп} производится исключение потенциальных решений, не удовлетворяющих условию:

По результатам сравнения вычисленного азимута Ψ_а и значения азимута, полученного, например, от датчика курса Ψ_ак, при его наличии, производится исключение потенциальных решений, не удовлетворяющих условию:

где ΔΨ_а - максимально допустимое значение погрешности оценки азимута,

определяющееся как сумма максимально допускаемой погрешности определения азимута по сигналам СРНС и предельной погрешности оценки азимута, полученной от датчика курса.

Оставшиеся после исключения потенциальные решения в дальнейшем подвергаются проверке с использованием дополнительных КА, не вошедших в начальное созвездие, в следующей последовательности:

1. Для каждого из оставшихся значений угловой ориентации объекта, в соответствии с используемой системой уравнений для определения углового положения (при s=4 система (13), при s=3 система (14)), вычисляют значения неоднозначностей дополнительных КА, которые не были использованы в начальном созвездии КА:

где i=s+1,…,n - текущий номер дополнительного КА, для которого осуществляется определение неоднозначности.

2. После определения неоднозначностей для всех дополнительных КА осуществляют повторное решение соответствующей системы уравнений для определения угловой ориентации с привлечением всех доступных измерений ФС по КА (число КА в системах (13) или (14) равно n). Решение системы уравнений выполняют, например, по методу наименьших квадратов, позволяющему решать избыточные системы уравнений.

3. После решения системы уравнений для n КА и нахождения уточненных значений неизвестных вычисляют значения функции правдоподобия для полученных значений неоднозначностей, относительных координат второй антенны и разности ГВЗ. Функция правдоподобия представляет собой условную плотность вероятности измеренных значений ФС (φ₁,…,φ_n) при условии подобранных неоднозначностей N₁,…,N_n и неизвестных параметров ориентации и разности ГВЗ антенно-приемных каналов. При некоррелированных, нормально распределенных погрешностях измерения ФС функция правдоподобия имеет вид:

где σ_i - среднеквадратическая погрешность измерения ФС сигнала i-го КА, выраженная в фазовых циклах.

Шаги 1-3 выполняются для всех оставшихся после отсева потенциальных решений, характеризующих возможные значения угловой ориентации. Из полученных потенциальных решений выбирается одно, имеющее максимальное значение функции правдоподобия W. Значение угловой ориентации, соответствующее максимуму W является оптимальным решением, с максимальной вероятностью соответствующим искомой ориентации объекта.

Следует отметить, что согласно [4] для некоррелированных измерений при нормальном законе распределения погрешностей оценка, оптимальная по критерию максимального правдоподобия, соответствует оценке, полученной по методу наименьших квадратов. В связи с этим, для упрощения вычислений, критерий выбора оптимального решения может быть сведен к виду:

В данном случае максимизация функции правдоподобия (20) сводится к минимизации показателя ее экспоненты, представляющего собой квадратичную форму Q (21).

Действительно, квадратичная форма (21) при правильно разрешенной неоднозначности будет принимать значения, определяемые только случайной погрешностью измерения ФС принятых сигналов. В условиях нормального функционирования СРНС значения случайных погрешностей измерения ФС принятых сигналов, переведенные в расстояния, оказываются существенно меньше длины волны принимаемых сигналов, равной 19 см, и согласно экспериментальным данным составляют около 1-2 см. Следовательно, величина также будет составлять единицы сантиметров.

При наличии неправильно разрешенной неоднозначности, когда один или несколько элементов вектора неоднозначности NN найдены неверно, соответствующий элемент суммы, образующей Q, станет приблизительно равен длине волны по расстоянию, что приведет к возрастанию Q.

В связи с этим значение угловой ориентации, соответствующее минимуму Q, с высокой вероятностью соответствует искомой угловой ориентации объекта. Вероятность соответствия оказывается тем выше, чем больше КА используется для оценки угловой ориентации. Данный факт объясняется тем, что при накоплении суммы квадратов невязок Q происходит усреднение случайных отклонений суммируемых величин, обусловленных погрешностями измерения ФС для каждого из КА.

С другой стороны, критерий поиска решения, соответствующего максимуму функции правдоподобия, может быть использован при распределении погрешностей измеренных значений ФС по закону, отличающемуся от нормального, а также при наличии взаимной корреляции погрешностей измерения ФС для сигналов разных КА. В этом случае изменяется вид функции правдоподобия W (20), однако поиск оптимального решения по-прежнему базируется на поиске максимума функции правдоподобия.

С целью дальнейшего повышения достоверности полученной оценки угловой ориентации может быть организовано вычисление и накопление значений W или Q по результатам т разновременных измерений для проверяемых возможных значений угловой ориентации, в результате чего обеспечивается уменьшение влияния случайных отклонений W или Q, вызванных погрешностями измерения ФС.

Устройство определения угловой ориентации (фиг.1), размещаемое на объекте и служащее для реализации предложенного способа, содержит два идентичных антенно-приемных канала, каждый из которых содержит последовательно соединенные приемную антенну 1₁ (1₂), малошумящий усилитель (МШУ) 2₁ (2₂), радиотракт 3₁ (3₂) и блок цифровой обработки сигналов 4₁ (4₂). Каждый из радиотрактов 3₁ (3₂) и блоков цифровой обработки сигналов 4₁ (4₂) своими вторыми входами подключены к формирователю опорных сигналов 5, вход которого соединен с выходом опорной частоты опорного генератора 6. Второй выход опорного генератора 6 подключен к входу синхронизации вычислительного блока 7, информационные входы которого соединены с выходами блоков цифровой обработки сигналов 4₁ и 4₂.

Сигналы n КА принимаются двумя разнесенными антеннами 1₁ и 1₂, усиливаются малошумящими усилителями 2₁ и 2₂, преобразуются в сигналы промежуточной частоты и усиливаются радиотрактами 3₁ и 3₂, после чего поступают в блоки цифровой обработки сигналов 4₁ и 4₂, где происходит разделение сигналов каждого из спутников. Блоки цифровой обработки 4₁ и 4₂ реализованы по схеме оптимального корреляционного приемника, на выходе которых формируются отсчеты корреляционных интегралов I и Q для сигналов каждого из КА. Значения корреляционных интегралов соответствуют результатам корреляционного перемножения принимаемых сигналов на синфазную и ортогональную составляющие опорного сигнала, синтезируемых формирователем опорных сигналов 5 для каждого из спутников. На вычислительный блок 7 возложены функции управления режимами работы приемника, включающими в себя поиск, захват сигналов по частоте и задержке, частотную и фазовую автоподстройку, синхронизацию по метке времени и границе бита служебной информации, прием и декодирование служебной информации, измерение радионавигационных параметров сигнала. К радионавигационным параметрам сигнала относятся его задержка, частота и фаза. Кроме управления режимами работы и измерения радионавигационных параметров вычислительный блок 7 решает задачи вторичной обработки измеренных параметров, заключающиеся в определении координат КА на момент проведения измерений (задача размножения эфемерид) на основе принятой служебной информации, вычисления координат места объекта и определения угловой ориентации антенной платформы. Также на вычислительный блок 7 возложена задача прогноза сеансов навигационных определений и управления режимами работы блоков 4₁ и 4₂ для КА, появляющихся в зоне радиовидимости или покидающих эту зону.

Координаты объекта определяются на основе измерений задержек сигналов, принятых от каждого КА. Для проведения таких измерений сигналы каждого КА модулируются псевдослучайными последовательностями (ПСП), называемыми дальномерным кодом. Путем сравнения ПСП сигнала, сформированного блоком 5, с ПСП принятого сигнала происходит определение времени задержки принятого сигнала. Дальность до КА, излучившего сигнал, получают путем умножения времени задержки на скорость распространения радиосигналов. Следует отметить, что, вследствие несовпадения бортового времени объекта с опорным временем спутниковой радионавигационной системы, эта дальность не равна геометрической и в связи с этим получила название псевдодальности. Координаты объекта на основе измеренных значений псевдодальностей получают путем решения системы уравнений вида

где x_ci, y_ci, z_ci - координаты i-го КА в геоцентрической системе координат, вычисленные на момент проведения измерений путем решения задачи размножения эфемерид;

R_i - измеренные значения псевдодальностей;

с - скорость распространения радиосигналов;

x, y, z - неизвестные координаты объекта в геоцентрической системе координат;

τ₀ - неизвестное расхождение шкалы времени объекта с системным временем спутниковой радионавигационной системы.

Система уравнений (22) содержит 4 неизвестных и для ее однозначного решения необходимо принять сигналы не менее 4-х КА. Способы решения таких систем рассмотрены, например, в [5, с.230-231].

Для определения угловой ориентации объекта вычислительный блок 7 производит оптимальную оценку начальных фаз сигналов, принятых антенно-приемными устройствами на основе значений корреляционных интегралов I и Q, накопленных на измерительном интервале по формуле

где

Ф начальная фаза принятого сигнала, имеющая диапазон однозначных измерений (-π,+π).

После оценки начальных фаз сигналов, принятых каждой из антенн, вычисляют значения ФС сигналов, принятых пространственно разнесенными антеннами в соответствии с выражением

где φ_i - значение ФС сигнала i-го КА, принятого разнесенными антеннами объекта;

Ф_2i Ф_1i - найденные в соответствии с (23) значения начальных фаз сигналов i-го КА, принятых соответственно антеннами 1₂ и 1₁ объекта. Значения ФС φ_i сигналов каждого из КА используются для определения углового положения осей измеряемого объекта путем решения систем уравнений (13) или (14) и поиска оптимального решения из всех перебираемых значений решений.

Блок-схема алгоритма р