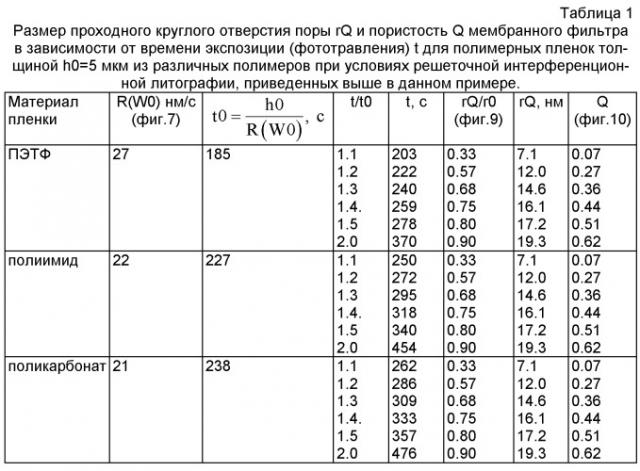
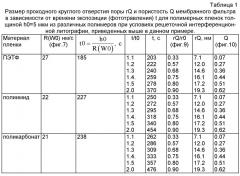
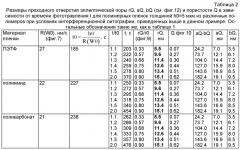
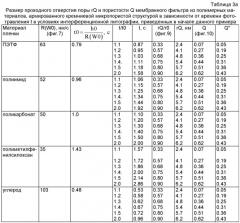
Способ изготовления мембранного фильтра

Способ изготовления мембранного фильтра

Иллюстрации

Показать все

Реферат

Изобретение относится к микроструктурным технологиям и может быть применено в нанотехнологии, медицине, химии, молекулярной биологии и оптике.

Одним из средств выделения и разделения наноразмерных частиц (например, белков, нуклеиновых кислот, клеток и субклеточных структур) являются мембранные фильтры. Мембранные фильтры представляют собой пористые перегородки с микронными и субмикронными порами, через которые проходит фильтруемая среда под действием перепада давления или концентрации (диффузия), а частицы, размер которых больше размера пор, остаются на перегородке.

Наиболее распространенные мембранные фильтры получают из эфиров целлюлозы (нитратов и ацетатов) по сложной технологии. Определенным образом приготовленные коллоидные растворы эфиров целлюлозы наносят тонким слоем на гладкую подложку, в определенном режиме испаряют растворители, и при этом получается мелкосетчатая структура. Характеристики этой структуры зависят от состава исходных растворов и режима испарения. Таким образом получают мембраны с размерами пор 10-100 нм (для ультрафильтрации), 1-10 нм (для нанофильтрации), 0.1 нм (для обратного осмоса). Мембраны, изготовленные этим способом, с порами размером менее 0,1 мкм, используемые для удаления мельчайших частиц из воды, от крупных органических молекул до ионов растворенных веществ, имеют незначительное проходное сечение, относительно высокое гидравлическое сопротивление (например, рабочее давление обратного осмоса 1-10 МПа (10-100 атм)), и поэтому для обеспечения заданной производительности требуются большие площади фильтрации. Поры имеют неправильную форму и большой разброс размеров пор, из-за чего такие мембраны более подходят для очистки сред от нано- и микрочастиц, нежели как сита (сито - это фильтр, с которого можно и легко отделить осадок, извлеченный из фильтруемой среды - жидкости, газа), т.к. частицы в значительной степени застревают в более крупных ячейках сетки.

Наиболее близкими к заявляемому техническому решению является способ получения т.н. «ядерных» или «трековых» мембран. Им в значительной степени не свойственно указанное «ситовое ограничение». Их изготавливают путем облучения полимерных пленок толщиной от 1 до 15 мкм из или полиэтилентерефталата (лавсан), или поликарбонатов или осколками деления ядер (т.н. «ядерные мембраны»), или ионами аргона в ускорителе частиц (т.н. «трековые мембраны»). При прохождении частицы через пленку из полимерного материала в ней образуется след (трек) в виде разрушенного полимера. Затем эти треки протравливают (удаляют разрушенный полимер) кислотой или щелочью и получают в пленке правильные цилиндрические отверстия одного и того же диаметра в диапазоне от 30 нм до 8 мкм (Т.Брок, Мембранная фильтрация, М., «Мир», 1987, стр.9, 59-61). Наиболее существенным недостатком этого способа является невозможность получения упорядоченной пространственной структуры пор из-за неупорядоченного пространственного распределения ионов в пучке и, соответственно, треков в полимерной пленке. Это обстоятельство является недостатком способа, потому что обусловливает недостаток конечного продукта - мембранного фильтра. Так, пространственная неупорядоченность получаемой структуры пор позволяет получать мембраны с небольшой (0.07÷0.1) пористостью (отношением площади проходного сечения пор к общей площади фильтра), т.к. увеличение плотности расположения пор на мембране приводит к наложению их друг на друга и получению отверстий больше заданного размера. Недостаточная пористость, в свою очередь, ухудшает расходную характеристику мембраны (зависимость расхода от давления). Также известный способ позволяет получать поры только цилиндрические, круглые в поперечном сечении и не позволяет получать эллиптические в поперечном и конические в продольном сечении. Между тем считается, что конические в продольном и эллиптические («щелевые») в поперечном сечении поры меньше подвержены «забиванию» частицами в процессе работы. Наконец, этот известный способ не позволяет получать нанопоры с диаметром менее 30 нм.

Целью данного изобретения является способ изготовления мембранного фильтра большой пористости (до 0.5÷0.6) с порами одинакового размера от 1 нм или больше или круглыми, или эллиптическими в поперечном и коническими в продольном сечении.

Технический результат, достигаемый данным предложением, состоит в способе изготовления мембранного фильтра большой (0.5-0.6) пористости с порами одинакового размера от 1 нм и больше или круглыми, или эллиптическими в поперечном и коническими в продольном сечении.

Указанный технический результат достигается тем, что в известном способе, включающем облучение полимерной пленки излучением, вызывающим локальную химическую деструкцию полимера и вытравливание (удаление) продуктов деструкции из облученных участков пленки,

облучение производят структурно упорядоченным синхротронным излучением с помощью системы решеточной интерференционной литографии

(H.H.Solak, C.David, J.Gobrecht, V.Golovkina, F.Cerrina, S.O.Kim, P.F.Nealey, Sub-50 nm period patterns with EUV interference lithography. Microelectronic Engineering, v.67-68 (2003), pp.56-62;

Beyer O., Nee I., Havermeyer F., Buse K. Applied Optics. 2003. Vol.42. N1. P.30-37; Cai L.Z., Yang X.L. Optical and Laser Technology. 2002. Vol.34. P.671-674; Egglet B.J. IEEE Journal of Selected Topics in Quantum Electronics. 2001. Vol.7. N.13. P.409-423; Harun H. Solak Laboratory for Micro and Nanotechnology, Paul Scherrer Institute, Switzerland Pushing the Limits of Nano-patterning with Extreme Ultraviolet Interference Lithography, http://lmn.web.psi.ch/xil/xil_pres.pdf)

в камере, заполненной газообразным водородом, благодаря чему травление (удаление) материала облученных участков, приводящее к образованию пор в пленке из полимерного материала, происходит во время облучения за счет образования летучих продуктов в результате фотохимической реакции между материалом пленки и водородом (далее этот процесс мы будем называть «фототравлением»).

Большая пористость мембранного фильтра в предлагаемом способе достигается благодаря упорядоченному регулярному расположению получающихся пор в мембране, соответствующему упорядоченной структуре интерферирующих пучков излучения (называемой далее «интерференционной картиной») после системы решеточной интерференционной литографии; эллиптичность поперечного сечения пор достигается выбором пар дифракционных решеток с разным периодом (с одинаковым периодом получаются круглые в поперечном сечении поры), а коничность продольного сечения пор обеспечивается специфичным неоднородным распределением плотности потока излучения в интерферирующих пучках излучения после системы решеточной интерференционной литографии, обусловливающим разную скорость фототравления материала полимерной пленки по поперечному сечению каждого упомянутого пучка излучения.

На фиг.1 показана схема четырехлучевой решеточной интерференционной литографии.

На фиг.2 показана схема интерференции пучков излучения от двух дифракционных решеток.

На фиг.3 показано распределение плотности потока излучения по поверхности пленки из полимерного материала после четырехлучевой системы решеточной интерференционной литографии (далее «интерференционная картина») с парами дифракционных решеток с разным периодом.

На фиг.4 показана структура интерференционной картины, полученной от пар дифракционных решеток с одинаковыми периодами на поверхности пленки из полимерного материала в 4-пучковой системе бесшаблонной интерференционной литографии с одинаковыми периодами пар дифракционных решеток.

На фиг.5 показано распределение плотности потока излучения в отдельной ячейке периодической структуры интерференционной картины, полученной от пар дифракционных решеток с одинаковым периодом.

На фиг.6 показана зависимость плотности потока излучения от расстояния от центра ячейки периодической структуры интерференционной картины, полученной от пар дифракционных решеток с одинаковым периодом.

На фиг.7 показана зависимость скорости фототравления для разных полимерных материалов от плотности потока излучения.

На фиг.8 показана зависимость продольного профиля поры мембранного фильтра от времени фототравления.

На фиг.9 показана зависимость радиуса проходного отверстия поры от времени фототравления.

На фиг.10 показана зависимость пористости мембранного фильтра от радиуса проходного отверстия поры.

На фиг.11 показана структура интерференционной картины на полимерной пленке при разном периоде пар дифракционных решеток системы решеточной интерференционной литографии.

На фиг.12 показана структура ячейки периодической структуры интерференционной картины на полимерной пленке, полученной при разном периоде дифракционных решеток.

На фиг.13 приведен пример технологической схемы изготовления мембранного фильтра из полимерного материала, армированного микропористой кремниевой структурой.

На фиг.14 приведен пример технологической схемы изготовления мембранного фильтра из неорганического материала, армированного кремниевой микропористой структурой.

На фиг.15 приведен пример технологической схемы изготовления мембранного цельнометаллического фильтра.

Осуществляют способ следующим образом.

Упорядоченную структуру пор в предлагаемом способе изготовления мембранного фильтра получают путем облучения (экспонирования) тонкой полимерной пленки узкополосным (Δλ/λ=2,5%) когерентным синхротронным излучением (СИ) с рабочей длиной волны в диапазоне 5÷100 нм. Такое излучение генерируется специализированным многополюсным ондулятором. Пространственное структурирование излучения на обрабатываемой (экспонируемой) полимерной пленке 1 осуществляют с помощью оптической системы 4-лучевой решеточной интерференционной литографии (схема на фиг.1), включающей квазишаблон 2, в котором располагают две взаимно перпендикулярные пары дифракционных решеток 3 и 4 с периодами РХ и PY соответственно. Интерференция 4-х пучков 1-го порядка, дифрагируемых на этих решетках, приводит к образованию на поверхности и в объеме пленки 1 стоячего электромагнитного поля 5 (интерференционной картины), периодического по координатам Х и Y с периодами DX и DY и однородного по координате Z на расстояниях порядка глубины резкости (ГР) интерференционной картины. Более детально схема формирования интерференционной картины 5 в методе решеточной интерференционной литографии иллюстрируется на фиг.2 на примере интерференции двух пучков синхротронного излучения первого дифракционного порядка (+1 и -1), прошедших, например, через пару решеток 3 (решетки 4 при этом предполагаются закрытыми от излучения). На фиг.2 для основных компонентов системы используются те же обозначения, что и на фиг.1. Кроме того, введены обозначения:

θ - угол между интерферирующими пучками +1 и -1;

α - угол дифракции пучков +1 и -1 на решетках;

1/2ГР - половина глубины резкости интерференционной картины.

Особенность интерференционной картины 5 состоит в большой глубине резкости (ГР) - около 100 мкм (фиг.2), что позволяет осуществлять процесс фотохимического травления без динамической фокусировки, необходимой при использовании других проекционных литографических систем.

Другой важной для реализации предлагаемого способа особенностью системы решеточной интерференционной литографии является ее полная ахроматичность, т.е. независимость размерных параметров формируемого электромагнитного поля (интерференционной картины) от длины волны. Эта особенность позволяет использовать оптимальную для осуществления фотохимической реакции длину волны в рабочем диапазоне 5-100 нм без зависимости размера пор в формируемом фильтре от длины волны (разумеется, при известном ограничении периода дифракционных решеток, который не может быть менее полудлины волны).

Упомянутая ахроматичность обусловлена тем, что изменение угла дифракции пучков α на решетках 3 при изменении длины волны λ приводит к такому изменению углов θ (фиг.2) между интерферирующими пучками, при котором остается неизменной результирующая интерференционная картина. Например, два дифракционных пучка 1-го порядка, формируемые решетками 3 (фиг.2), составляют угол α с нормалью к решеткам 3, причем

где РХ - период решеток в паре 3, λ - длина волны излучения. Поэтому эти пучки составляют между собой угол θ=2α. Если бы рассматривалась интерференция только этих двух пучков, то они формировали бы одномерную интерференционную картину (вдоль оси X) с периодом

С учетом соотношения (1) получаем период дифракционной картины

т.е. независимо от длины волны формировалось бы одномерное стоячее электромагнитное поле, период которого вдвое меньше периода решеток в данной паре. При использовании дифракционных пучков 2-го порядка

Формулы (1)-(4) точно описывают двухпучковую интерференцию, которая здесь рассмотрена для иллюстрации основных особенностей метода решеточной интерференционной литографии. Кроме того, двухпучковую интерференционную литографию используют в предлагаемом способе для изготовления дифракционных решеток с нужным периодом путем многократного последовательного уменьшения периода имеющихся решеток (H.H.Solak, C.David, J.Gobrecht, V.Golovkina, F.Cerrina, S.O.Kim, P.F.Nealey, Sub-50 nm period patterns with EUV interference lithography, Microelectronic Engineering, v.67-68 (2003), pp.56-62).

В реально используемой оптической системе из двух взаимно перпендикулярных пар дифракционных решеток 3 и 4 (фиг.1) с периодами РХ и PY интерферируют сразу 4 вторичных дифракционных пучка. Они создают стоячее электромагнитное поле (интерференционную картину) с периодическим двумерным распределением относительной плотности потока излучения W/W0 в плоскости пленки 1 (фиг.3), причем для дифракционных пучков 1-го порядка периоды DX и DY интерференционной картины вдоль осей Х и Y в этом случае равны соответствующим периодам РХ и PY пар дифракционных решеток (а не РХ/2 и PY/2, как в случае двухпучковой интерференции на отдельной паре решеток) и также не зависят от длины волны.

На трехмерном графике фиг.3 представлена интерференционная картина 5 для частного случая, в качестве примера, когда период дифракционных решеток 4 вдвое больше периода решеток 3: PY=2PX, т.е. для DY=2DX, в трехмерном пространстве, где координаты Х и Y задают точку поверхности полимерной пленки 1, а значение соответствующей координаты Z=Z(X,Y) - величину нормированной плотности потока W/W0 в этой точке пленки, где W0 - максимальное значение плотности потока. На фиг.3 размеры интерференционной картины вдоль осей Х и Y нормированы на величину периода РХ.

На двумерном графике фиг.4 приведено такое же распределение для частного случая одинаковых шагов пар дифракционных решеток РХ=PY, представленное с помощью линий 6 одинаковой плотности W/W0 потока излучения (указана числом в разрыве линии) в проекции на поверхность полимерной пленки (по аналогии с линиями одинаковой высоты -«горизонталями» в картографии). При использовании пар дифракционных решеток с равными периодами PX=PY=P периоды DX и DY двумерной дифракционной картины одинаковы: DX=DY=D, причем при интерференции пучков 1-го порядка D=P (при интерференции 2-го порядка D=P/2), а линии равной плотности потока излучения 6 образуют концентрические квазиокружности, располагающиеся в шахматном порядке (фиг.4). Эти концентрические квазиокружности 6 фактически оказываются упорядоченными в периодической структуре из квадратных ячеек 7, в системе координат (x, y), повернутой на угол 45° относительно исходных осей Х и Y, с периодом, который мы обозначим как 2r0. Как видно из фиг.4,

а при интерференции пучков 2-го порядка D=P/2 и

Параметр 2r0 определяет размер квадратной ячейки 7 периодической структуры интерференционной картины 5 и, следовательно, максимальный теоретически возможный поперечный размер поры при использовании дифракционных решеток с заданным периодом Р. Таким образом, порядок размера пор в предлагаемом способе определяется периодом применяемых дифракционных решеток Р по формулам (5) и (6). Распределение плотности потока излучения W/W0 в отдельной ячейке 7 этой структуры показано на фиг.5, где

r - расстояние от центра ячейки 7, или радиус окружности, образуемой линией, равной плотности потока излучения 6,

r/r0 - нормированное (для общности рассмотрения) расстояние от центра ячейки 7 на ½ длины стороны ячейки.

Для больших значений плотности потока (вблизи центра ячейки) линии, равной плотности 6, с большой точностью являются окружностями. По мере удаления от центра ячейки форма этих линий немного отклоняется от формы окружности. На фиг.6 приведено изменение нормированной плотности потока излучения W/W0 от величины нормированного радиуса r/r0 в направлении, параллельном стороне ячейки 7 - r и под углом 45° к ней - r45.

Различие кривых на графике фиг.6 становится заметным только на краях ячейки при W/W0<0.2. Эта область, как правило, будет находиться вне области формируемого отверстия в ячейке (отдельной поры), поэтому для большинства практических применений можно аппроксимировать форму линий равной плотности потока 6 окружностью с радиусом r.

В этом случае плотность потока излучения можно рассматривать как функцию одной переменной - радиуса соответствующей аппроксимирующей окружности в ячейке:

W=W(r).

Процесс фотохимического формирования мембранного фильтра осуществляют следующим образом. Пленку из полимерного материала 1, например, такого как или полиэтилентерефталат (ПЭТФ), или полиимид, или поликарбонат, или полисилоксан, или углерод, помещают в фокус оптической системы интерференционной литографии (фиг.1). Пусть заданы длина волны излучения λ, максимальная плотность потока излучения W0, a зависимость скорости фототравления R от плотности потока излучения W для выбранного материала пленки и длины волны излучения известна или предварительно определена экспериментально (например, см. фиг.7), периоды дифракционных решеток РХ и PY выбраны в соответствии с типом и целевыми размерными параметрами изготавливаемого мембранного фильтра. Камеру заполняют реакционным газом, предпочтительно водородом, образующим с материалом пленки под действием излучения летучие вещества. Возможно использовать для этого и некоторые другие газы, например кислород, хлор, фтор. Однако водород предпочтителен благодаря самому малому молекулярному весу. Его молекулы имеют самую большую скорость теплового движения (1700 м/с при нормальных условиях, а молекулы кислорода - всего 425 м/с), что обеспечивает более быстрый их транспорт в зону реакции. Кроме того, при фотореакции с полимерами водород образует вещества с меньшим молекулярным весом: метан -СН₄ (М.в.=16), воду -Н₂О (М.в.м18), аммиак -NH₃ (М.в.=17), силан -SiH₄ (M.в.=32), что обеспечивает их более быстрый транспорт из зоны реакции.

Например, ниже приведены брутто реакции фототравления полимеров (в расчете на мономерное звено полимера) в атмосфере водорода:

полиэтилентерефталата (лавсана) - C₁₀H₈O₄+20H₂=10CH₄+4H₂O;

поликарбоната (эфира бисфенола А) - C₁₆H₁₄O₃+28Н₂=16СН₄+3H₂O;

полиимида - C₁₆H₁₄O₄N₂+32Н₂=16СН₄+4H₂O+2NH₃;

полиметилфенилсилоксана - C₇H₈OSi+12H₂=7CH₄+H₂O+SiH₄;

углерода - С+2Н₂=СН₄.

В то время как, например, в реакции с кислородом образовывалось бы много углекислого газа CO₂ (М.в.=44), а фототравление полиметилфенилсилоксана привело бы к образованию двуокиси кремния - продукта отнюдь не летучего. Наконец, весьма важно, что водород гораздо меньше, чем другие газы поглощает излучение в диапазоне 5-100 нм, что обеспечивает практическое отсутствие потерь потока излучения в камере.

Рабочее давление водорода выбирают таким, чтобы, прежде всего, был обеспечен с избытком его подвод в зону реакции для обеспечения реакции гидрирования при разрыве химических связей в полимере под действием излучения. Поэтому необходимый поток водорода в зону реакции будет зависеть от плотности потока излучения W: чем больше плотность потока излучения, тем больше будет скорость разрыва связей полимера и тем больше нужно водорода для их насыщения. При достаточном количестве водорода, полностью обеспечивающем насыщение разорванных связей (реакции нулевого порядка по водороду), пространственное распределение скорости фототравления полимера в плоскости пленки будет пропорционально распределению плотности потока излучения:

где

R(r) - распределение по радиусу r (см. фиг.5) скорости фототравления полимера в плоскости пленки 1;

А - константа, зависящая от материала пленки (см. фиг.7);

W(r) - распределение по радиусу r плотности потока излучения (см. фиг.6).

Необходимое давление водорода вычисляют предпочтительно на основе молекулярно-кинетической теории газов, и для реальных плотностей излучения в диапазоне W0=50÷500 мВт/см² (в реальной системе интерференционной литографии) давление водорода может составлять 0.5÷2 Па. При таких давлениях влияние поглощения излучения водородом на скорость фототравления полимера в рабочем диапазоне длин волн пренебрежимо мало. Камера предпочтительна проточная, с постоянной откачкой и напуском водорода для удаления из камеры продуктов реакции и поддержания концентрации водорода постоянной.

Фототравление происходит по законам изотропного травления. В каждый момент времени скорость дальнейшего распространения фронта травления в каждой точке r текущего фронта определяется локальной скоростью R(r). Профили (продольные сечения) формируемой поры (фиг.8) в отдельной ячейке получены путем численного решения уравнения распространения фронта волны - аналога уравнения эйконала, описывающего распространение фронта световой волны в среде с переменным показателем преломления (Лаврук В.Н., Мануйлов В.В., Матвеев В.М., Модели проявления рентгенорезистов, Электронная техника. Серия 3. Микроэлектроника, вып.1 (140), 1991, стр.35-38), и представлены на фиг.8.

На фиг.8 введены обозначения:

h0 - толщина полимерной пленки;

Z/h0 - текущая координата по оси Z (на фиг.1), отсчитываемая от нижней поверхности полимерной пленки и нормированная на толщину пленки (на нижней поверхности пленки Z/h0=0, на верхней - Z/h0=1);

строчные буквы а-д отмечают профили нанопоры в процессе фототравления для определенных моментов времени t, нормированных на время t0 протравливания пленки на всю толщину h0 в центре ячейки, где скорость травления максимальна:

а - t/t0=1.1, б - t/t0=1.2; в - t/t0=1.3; г - t/t0=1.4, д - t/t0=1.5.

Время t0 определяют путем деления толщины полимерной пленки h0 на известную заранее (например, из фиг.7) скорость травления для данного материала полимерной пленки 1 при имеющейся максимальной плотности потока излучения W0, соответствующей центру ячейки:

Из фиг.8 видно, что получающиеся поры расширяются в разной степени при разных временах фототравления t/t0 от нижней поверхности полимерной пленки к верхней и их условно можно считать коническими.

Из фиг.8 видно, что проходной радиус формируемой поры, т.е. радиус поры на нижней границе пленки, обозначенный в нормированном виде как rQ/r0 (он указан для профиля а), определяющий пористость Q изготавливаемого мембранного фильтра, задается надлежащим выбором значения нормированного времени фототравления t/t0. Зависимость этого радиуса от времени rQ/r0=rQ/r0(t/t0), полученная теми же численными методами, что и профили фототравления на фиг.8, представлена на фиг.9.

Таким образом, в полимерной пленке 1 формируется упорядоченная структура пор мембранного фильтра, соответствующая структуре интерференционной картины 5 (см., например, фиг.4), формируемой системой решеточной интерференционной литографии (см. фиг.1).

В этой упорядоченной структуре пор пористость определяется как отношение площади проходного отверстия поры к площади ячейки:

где Q - пористость;

rQ - радиус проходного отверстия поры (см. фиг.8);

2r0 - сторона ячейки 7 или период периодической структуры (см. фиг.4);

π(rQ)² - площадь проходного сечения поры;

(2r0)² - площадь ячейки 7 (см. фиг.5):

После упрощения уравнения (9)

Эта зависимость приведена на графике фиг.10.

Предельное значение пористости (при rQ=r0) в системе круглых пор составляет

Таким образом, пористость в предлагаемом способе для пор с круглым поперечным сечением (при одинаковых периодах пар дифракционных решеток) определяется радиусом проходного отверстия поры, который получают, выбирая соответствующее время фототравления (при известной заранее зависимости скорости фототравления для данного полимера от плотности потока излучения).

Мы рассмотрели получение мембранного фильтра с круглыми в поперечном сечении порами с применением системы решеточной интерференционной литографии с парами дифракционных решеток (3 и 4 на фиг.1) с одинаковым периодом. Применяя решетки с разным периодом, можно аналогично получить поры квазиэллиптического поперечного сечения. Например, на фиг.11 показана структура интерференционной картины 5 для случая применения пар решеток 3 и 4 с периодами PY=2PX (обозначения аналогичны обозначениям на фиг.4).

В этом случае также образуется показанная на фиг.11 периодическая структура интерференционной картины 5 (фиг.1), аналогичная рассмотренному выше случаю (фиг.4) с применением пар дифракционных решеток с равными периодами.

Но в этом случае ячейки 7 (фиг.11) периодической структуры интерференционной картины представляют собой ромбы со стороной, равной 2r0, она же - период упорядоченной структуры интерференционной картины 5. Линии равной плотности потока 6 (показана только одна линия на ячейку) образуют концентрические эллипсы (точнее квазиэллипсы, аналогично квазиокружностям на фиг.4).

На фиг.12 показана ячейка 7 периодической структуры интерференционной картины 5, где 8 - эллипс, вписанный в ячейку 7, 6 - один из эллипсов равной плотности излучения, 2r0 - сторона ячейки, или период периодической структуры интерференционной картины 5 (фиг.1), r - расстояние от центра ячейки до точки пересечения с эллипсом равной плотности излучения (rQ - до пересечения с краем проходного отверстия эллиптической поры) по линии r0, a0, b0 - полуоси вписанного в ячейку 7 эллипса 8, а а и b соответственно полуоси произвольного эллипса 6 одинаковой плотности излучения, aQ и bQ - полуоси проходного отверстия поры. Значениями r и r0 в случае получения эллиптических пор пользуются для определения характеристик так же, как ранее для случая круглых (фиг.8, 9, 10).

Однако, если у проходного отверстия круглой поры одна характеристика - диаметр 2rQ или радиус rQ, то у эллиптической две - большая и малая полуось - aQ и bQ. Поэтому возникает необходимость выразить их через r и r0. Для такой связи воспользуемся второй теоремой Апполония (http://www.pm298.ru/ellips18.php). которая утверждает, что площадь ромба S, например, ячейки 7 на фиг.12, описывающего эллипс, например эллипс 8, с полуосями а0 и b0

S=4a0b0. С другой стороны, площадь ромба 7 равна половине произведения его диагоналей:

S=PxPy/2,

где Px Py - периоды дифракционных решеток в случае использования интерференции 1-го порядка (в случае интерференции 2-го порядка следует в выражение подставить вместо Px, Py-Px/2, Py/2).

Приравнивая значения площадей ромба 7

,

С другой стороны, из фиг.11 по теореме Пифагора видно:

Разделив уравнение (13) на уравнение (12) и проведя простые преобразования, получим

Уравнение 14 устанавливает связь между полуосями и полудлиной стороны ячейки, а проще между осями вписанного в ячейку 7 эллипса 8 - 2а0, 2b0 и стороной ячейки 2r0 периодической структуры, учитывая, что отношение осей эллипса задается отношением периодов дифракционных решеток Px и Py.

По принципу подобия для произвольного эллипса 6 равной плотности излучения (фиг.12)

где

a, b - значения полуосей эллипса равной плотности потока излучения,

r - расстояние от центра ячейки периодической структуры до середины стороны ромба, описывающего эллипс равной плотности излучения с полуосями a и b, а для проходного отверстия поры

Используя вышеприведенную теорему Апполония для площади ромба, описывающего эллипс, и известную формулу для площади эллипса, можно определить максимальную возможную пористость фильтра с эллиптическими порами:

где Q_max - максимальная возможная пористость фильтра,

а0, b0 - полуоси эллипса 8, вписанного в ячейку периодической структуры 7;

π·а0·b0 - площадь вписанного в ячейку периодической структуры эллипса 8;

4a0·b0 - площадь ромба, описывающего эллипс 8 с полуосями а0, b0 по вышеприведенной теореме Апполония. Таким образом, максимальная достижимая пористость одинакова для фильтра с круглыми и эллиптическими порами и не зависит от отношения осей последних.

Проведенные выкладки позволяют при осуществлении предлагаемого способа в случае эллиптических пор применять параметры t/t0, rQ/r0, приведенные выше на фиг.8, 9, 10 для круглых пор.

При экспонировании полимерной пленки 1 в атмосфере водорода получают упорядоченную структуру эллиптических пор в мембранном фильтре, соответствующую структуре интерференционной картины 5 на полимерной пленке 1, сформированной системой решеточной интерференционной литографии (фиг.1). Возможность изготовления предлагаемым способом мембранного фильтра с эллиптическим порами, относящимися к так называемым «щелевым», является весьма полезным техническим результатом, т.к. известно, что поры такой формы при фильтрации забиваются меньше из-за того, что вероятность перекрывания частицей полностью сечения поры, в случае щелевой поры гораздо меньше, чем в случае круглой. Кроме того, такие «эллиптические» фильтры (сита) могут оказаться эффективным средством разделения по форме (центросимметричных и осесимметричных) близких по размеру наночастиц.

Необходимым условием реализации предлагаемого способа изготовления мембранных фильтров с использованием решеточной интерференционной литографии является высокая степень когерентности излучения ондулятора (близкая к 100%). Поскольку степень когерентности уменьшается с уменьшением длины волны, для лучших современных источников приемлемый диапазон длин волн начинается с 5 нм. Верхняя граница рабочего диапазона не может быть больше 100 нм из-за резкого возрастания поглощения излучения в компонентах системы при дальнейшем увеличении длины волны. Кроме того, чем меньше длина волны излучения, тем больший диапазон размеров пор мембранного фильтра можно получить на ней из-за ограничения величины шага интерференционных решеток, которая не может быть менее половины длины волны. Предпочтительна длина волны - вблизи 10 нм. В частности, целесообразно использовать длину волны 13,4 нм, на которой работают лучшие интерференционные многослойные зеркала Mo/Si. В конкретных реализациях предлагаемого способа такие зеркала могут понадобиться для управления пучками излучения (кроме того, на этой длине волны в принципе возможна реализация не только решеточной, но и зеркальной системы интерференционной литографии).

Для нанопористых фильтров характерно большое сопротивление фильтрации, преодоление которого требует давления в десятки атмосфер. Это сопротивление пропорционально длине поры (толщине фильтра) и обратно пропорционально квадрату диаметра поры. При этих условиях целесообразно для уменьшения сопротивления мембранного фильтра изготавливать его как можно тоньше. Минимальная возможная толщина мембранного фильтра определяется технологическими возможностями изготовления пленки минимальной толщины, которая в настоящее время составляет значительно менее 100 нм, как для полимеров, так и для металлов, и для неорганических материалов. Однако практическое использование фильтров такой толщины представляется нереальным как в отношении возможности технологического манипулирования такой тонкой пленкой, так и в отношении возможности ее применения (вследствие малой собственной прочности) для фильтрации при реальном давлении.

Поэтому в предлагаемом способе реализуют концепцию армированного мембранного фильтра 9 (см. фиг.13) с нанопорами 10, изготовленного из, например, тонкой (менее 100 нм) полимерной пленки 1, закрепленной на армирующей структуре 11 достаточно большой толщины (порядка от 10 до 50 мкм) с упорядоченной структурой пор 12 микронного размера (например, с диаметром от 10 до 100 мкм). При дальнейшем рассмотрении армированных мембранных фильтров для удобства различения мы будем называть пленочную часть его 9 «нанопористым мембранным фильтром», поры 10 в нем - «нанопорами», а поры 12 в армирующей структуре 11 - «микропорами» в соответствии с их характерными размерами. Технологическая схема изготовления аналогичных армированных микропористой структурой мембранных нанопористых фильтров из неорганических материалов и металлов приведены на фиг.14 и 15.

Армирующая структура 11 из микропор 12 (см., например, фиг.13) обеспечивает многократное увеличение прочности мембранного нанопористого фильтра 9. Выдерживаемый им перепад давлений определяется теперь прочностью мембраны из тонкой полимерной пленки в отдельной микропоре 12 армирующей структуры 11. Например, для круглой микропоры 12 диаметром d и мембраны на ней толщиной h0 связь между перепадом давления р на мембране, прогибом мембраны s и полным напряжением σ в материале мембраны определяется хорошо известными формулами (Effect of stress on the stability of X-ray masks. M.Karnezos. J.Vac.Sci.Nechnol., В 4(1), 1986)

где σ0 - начальное напряжение в мембране (зависит от технологии и рабочей температуры),

Е=8·E0/3(1-ν) - эффективный модуль упругости круглой мембраны,

E0 и ν - модуль Юнга и коэффициент Пуассона материала мембраны соответственно. Исключая s из (18а) и (18б), получаем

Таким образом, максимальное давление, выдерживаемое мембраной, обратно пропорционально диаметру d микропоры 12.

Для определения максимально возможного перепада давлений на мембране нужно подставить в (18) разрывное напряжение материала мембраны (например, полимерной пленки). Например, для пленки полиимида толщиной 50 нм на микропоре диаметром 10 мкм для типичных значений Е₀=4000 МПа, ν=0,4 и разрывного напряжения σ=100 МПа при нулевом начальном напряжении σ₀ получаем

р=60 МПа=600 атм.

Начальные напряжения приводят к уменьшению максимально возможного давления. Но если начальное напряжение составляет даже 50% от разрывного напряжения (реальные начальные напряжения в большинстве случаев намного меньше), то максимально допустимый перепад давлений уменьшается всего лишь в 1,4 раза.

Масштабируемость результата, определяемого формулой (18) при изменении h0 и d, очевидна. Поэтому можно, например, сделать вывод, что рабочий перепад давлений р=100 атм будет выдерживаться при 6-кратном увеличении диаметра d микропор в армирующей микропористой структуре (до 60 мкм). С другой стороны, можно уменьшать толщину пленки h0, сохраняя прочность, до примерно нескольких нанометров, уменьшая диаметр микропоры d, на которой она размещается.

Таким образом, видно, что мембрана толщиной в несколько десятков нанометров, закрепленная на микропоре диаметром в несколько десятков микрон, может выдерживать довольно значительные давления, порядка десятков атмосфер. Поэтому нет необходимости в этом варианте реализации мембранного фильтра изготовлять его из пленок толще чем 100 нм (условный диапазон размеров нанообъектов). Такие армированные микропористыми структурами мембранные нанопорист