Способ определения упругих характеристик горной породы по данным измерений в скажине

Способ определения упругих характеристик горной породы по данным измерений в скажине

Иллюстрации

Показать все

Реферат

Изобретение относится к технологии бурения скважин, а именно к определению естественных упругих характеристик горных пород в условиях залегания, необходимых для выполнения технологических расчетов.

С использованием данных о величине фактического коэффициента бокового распора λ_ф проводятся прочностные расчеты стенок скважины для проектирования мероприятий по предупреждению гидроразрыва скважины при бурении и цементировании, осыпания и разрушения стенок. В связи с бурением наклонных скважин с большими углами искривления и горизонтальных возникла необходимость расчета деформирования сечения скважины, т.к. круглое сечение скважины, образованное долотом, становится эллиптическим при дальнейшем углублении скважины. Такое деформирование создает опасность заклинивания долота при подъеме из скважины и затрудняет спуск обсадной колонны (Попов А.Н., Могучев А.И., Попов М.А. Деформирование стенок наклонной скважины и его влияние на работу и изнашивание буровых долот // НТЖ. Строительство нефтяных и газовых скважин на суше и на море. - М.: ОАО "ВНИИОЭНГ", 2008. - №3. С.6-13). Величина деформации зависит не только от фактического коэффициента бокового распора, но и от модуля упругости горной породы в условиях залегания, т.е. в условиях сложного напряженного состояния. В качестве такого модуля целесообразно использовать модуль упругости С, соответствующий определяемому при статическом вдавливании штампа.

Известен способ определения естественных напряжений в горных породах как в идеально упругих телах (Сельващук А.П., Бондаренко А.П., Ульянов М.Г. Прогнозирование давления открытия поглощений при бурении на месторождениях Восточной Украины /Обзорная информация. - Сер. Бурение нефтяных и газовых скважин. - М.: ВНИИЭгазпром, 1981. - С.8-18). Вертикальная компонента р_г (геостатическое давление) на рассматриваемой глубине определяется по величине средневзвешенной плотности вышележащих горных пород. Горизонтальная компонента Р_б (боковое давление) прямо пропорционально геостатическому давлению:

где λ_У - коэффициент бокового распора упругой модели горной породы:

где µ - модуль поперечной деформации (коэффициент Пуассона), определяемый при испытаниях кернов горной породы на одноосное сжатие.

Недостатками этого способа являются: во-первых, в осадочных горных породах большую роль играет релаксация напряжений, в результате которой в общем случае λ_ф не равен λ_у, а лежит в интервале

во-вторых, способ не предусматривает определение модуля упругости С горной породы.

Наиболее близким техническим решением к заявляемому изобретению является способ определения упругих характеристик горной породы по данным измерений в скважине. Для этого после достижения скважиной изучаемого пласта в нем соосно бурят опережающую скважину меньшего диаметра и в нее спускают измерительный зонд (деформометр). Затем опережающую скважину обуривают методом колонкового бурения. Полученный в виде полого цилиндра керн вместе с зондом извлекают на поверхность. Извлеченный деформометр содержит данные о деформации горной породы в скважине и на поверхности. Извлеченный керн используют для определения коэффициента Пуассона методом аналогий или прямыми испытаниями. По данным замеров деформации керна горной породы с учетом геостатического давления, давления бурового раствора в скважине и коэффициента Пуассона составляют систему уравнений и расчетным путем определяют фактические упругие характеристики горной породы (Виттке В. Механика скальных пород. - М.: Недра, 1990. - С.292-323).

Недостатками этого способа является то, что он очень сложен и дорог. Способ предусматривает остановку бурения и соответствующее изменение компоновки инструмента. Для измерения деформаций горной породы в нескольких точках пласта потребуется соответствующее количество измерений в скважине и на поверхности. В осадочных горных породах низкой и средней прочности формирование в скважине керна в виде полого цилиндра весьма проблематично. Поэтому этот способ в глубоких скважинах не применяется.

Изобретение решает техническую задачу определения упругих характеристик горной породы по данным замера в скважине радиального смещения (деформации) стенок наклонной или горизонтальной скважины после вскрытия скважиной заданного интервала пласта.

Указанная задача решается тем, что в способе определения упругих характеристик горной породы по данным измерений в скважине, включающем определение коэффициента Пуассона (µ) методом аналогий, геостатического давления (р_г) и гидростатического давления бурового раствора (р_с) на рассматриваемой глубине, согласно изобретению в пределах заданного интервала пласта в статистически значимом количестве поперечных сечений по данным кавернометрии определяют радиальные смещения боковой и верхней стенок наклонной скважины как разности измеренных и номинального (R_H) радиусов скважины в двух взаимно перпендикулярных направлениях, рассчитывают среднеарифметические значения, среднеквадратические отклонения и доверительные интервалы смещений стенок скважины, а затем назначают область влияния скважины с радиусом контура R_к≥50R_н, разбивают текущие радиусы в направлении от боковой и верхней стенок на n элементов толщиной h=0,10R_н, составляют две системы уравнений для боковой стенки и для верхней стенки, связывающие соответствующие смещения стенок скважины с упругими характеристиками горной породы, с геостатическим давлением и гидростатическим давлением бурового раствора и углом искривления скважины, и решают обе системы совместно методом последовательных приближений относительно модуля деформации С и фактического коэффициента бокового распора λ_ф горной породы с заданной точностью.

Возможность применения предлагаемого способа определения упругих характеристик горной породы по данным измерений в наклонных и горизонтальных скважинах обусловлено неосесимметричным напряженным состоянием окружающих горных пород относительно оси скважины, что позволяет получить не менее двух замеров смещения стенок в одном поперечном сечении скважины при соответственно разных напряженных состояниях, которые необходимы для последующего расчета двух характеристик λ_ф и С. В вертикальной скважине смещение стенок невелико, практически осесимметрично и его измерение не достаточно для определения двух упругих характеристик горной породы. По мере увеличения угла искривления скважины α (зенитного угла) величины смещения стенок по абсолютной величине и их отличие друг от друга быстро возрастают и достигают максимума в горизонтальной скважине. В случае λ_ф=1 в любой скважине упругое смещение стенок скважины осесимметрично и равно

где ΔR - радиальное смещение стенки скважины; р_с - гидростатическое давление бурового раствора в скважине на рассматриваемой глубине. Для расчета смещений боковой ΔR_б и верхней ΔR_в стенок наклонной и горизонтальной скважины применено численное интегрирование в пределах области ее влияния (Попов А.Н., Могучев А.И., Попов М.А. Деформирование стенок наклонной скважины и его влияние на работу и изнашивание буровых долот // НТЖ. Строительство нефтяных и газовых скважин на суше и на море. - М.: ОАО "ВНИИОЭНГ", 2008. - №3. С.6-13).

Такое определение упругих характеристик горной породы позволяет решить задачу повышения надежности прочностных расчетов стенок скважины и прогнозирования опасности заклинивания породоразрушающего инструмента при подъеме из скважины.

Сопоставительный анализ с прототипом показывает, что заявляемый способ определения упругих характеристик горной породы отличается тем, что расчет характеристик проводится по статистическим данным измерений радиусов наклонной или горизонтальной скважины в двух взаимно перпендикулярных направлениях.

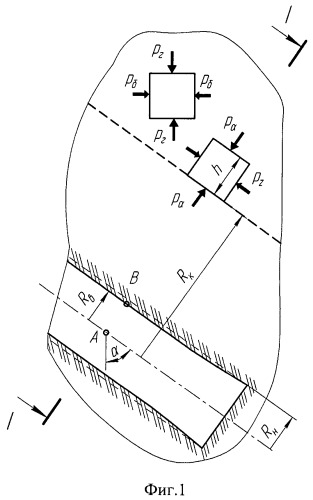
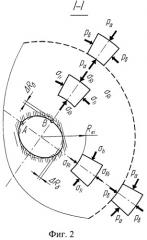
На фиг.1 показана схема наклонной скважины в разрезе и компоненты горного давления в массиве и на контуре влияния скважины. На фиг.2 показано поперечное сечение скважины плоскостью I-I и компоненты напряжений внутри контура влияния скважины в направлении от боковой (от т. А) и от верхней (от т. В) стенок скважины. Решение выполнено в цилиндрической системе координат с аппликатой z, совпадающей с осью скважины. На элемент внутри контура действуют радиальная σ_R и тангенциальная σ_t компоненты напряжений.

Из фиг.1 следует, что действующее на выделенный на контуре элемент радиальное давление над верхней стенкой и тангенциальное давление на выделенный элемент сбоку от стенки скважины (фиг.2) в соответствии с правилами сопромата равно

Тангенциальное давление, действующее на выделенный на контуре элемент над верхней стенкой, и радиальное давление сбоку от стенки лежат в горизонтальной плоскости и равны p_б=λ_фр_г (фиг.2). Компонента р_z на контуре и σ_z внутри контура определены при допущении о плоской деформации горной породы при вскрытии ее скважиной.

Элементу на контуре присвоен индекс l, а на стенке скважины индекс n. Тогда средний радиус i-го элемента

где R_ki - радиус контура i-го элемента; ΔR_i - радиальная деформация i-го элемента; h - толщина элемента.

Формула для расчета радиальной деформации i-го элемента в соответствии с законом Гука имеет вид

Сумма ΔR_i равна радиальному смещению стенки, т.е.

Тогда система уравнений для боковой стенки принимает вид

и для верхней стенки принимает вид

где R_0i=R_i/R_н; M=(p_α+λ_фр_г)/2; N=(p_α-λ_фр_г)/2.

Расчеты ΔR выполнены с использованием системы Excel. Вид программы с примером расчета для поперечного сечения I-I скважины (глубина по вертикали 2420 м, угол α=70°), пробуренной в Западной Сибири, приведен в таблице 1. Рассматриваемое сечение принадлежит интервалу бурения, сложенному в основном плотными глинами, для которых коэффициент Пуассона принимают равным 0,35. Если α=0, то результаты расчета соответствуют вертикальной скважине, а если α=90°, то горизонтальной скважине. В таблице 1 основная часть строк скрыта. Выбор радиуса контура R_к=50R_н и толщины h=0,10R_н обеспечил ошибку вычислений в пределах 2,5%. Для повышения точности вычислений следует увеличить радиус контура.

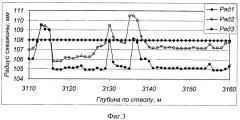
Способ осуществляют следующим образом. После вскрытия пласта бурением снимается кавернограмма ствола скважины в двух взаимно перпендикулярных направлениях, которая представляет собой два ряда замеренных размеров поперечных сечений скважины. Нетрудно показать, что в соответствии с принципом наименьшего действия один замер соответствует минимальному, а второй замер максимальному размеру сечения. Пример замера приведен на фиг.3.

Таблица 1
Расчет смещений стенки скважины
Исходные данные
Рг, МПа	57,0000
α, градус	70,0000	α, радиан	1,221
Рα, МПа	54,9353
µ	0,3500
λу	0,5385	рбу, МПа	30,692
λф	0,6914	рб, МПа	39,410
С, МПа	1867
		М, МПа	47,173
		N, МПа	7,763
рс, МПа	27
Rc, мм	108
Rк/RC	50	n	490
h0	0,10	h, мм	10,8

Боковая стенка

Rкi	Ri	ΔσRбi	Δσtбi	ΔRi	Сумма Δ Ri
5400		0	0	0	0
5389,2	5394,60	-0,00436	-0,00809	0,000000	0,000000
5378,4	5383,80	-0,00437	-0,00812	0,000000	0,000000
5367,6	5373,00	-0,00439	-0,00815	0,000000	0,000000
129,6	134,69	2,63339	-22,59881	-0,085625	-0,399514
118,8	123,80	5,20899	-28,83983	-0,119963	-0,519477
108	112,88	9,55632	-37,98037	-0,173583	-0,693060

Верхняя стенка

Rкi	Ri	ΔσRвi	Δσtвi	ΔRi	Сумма ΔRi
5400		0	0	0	0
5389,2	5394,60	0,02053	-0,00808	-0,000144	-0,000144
5378,4	5383,80	0,02061	-0,00811	-0,000144	-0,000288
5367,6	5373,00	0,02069	-0,00815	-0,000145	-0,000433
129,6	132,61	23,73108	-3,13411	-0,147039	-2,541929
118,8	121,66	25,90453	-1,43407	-0,154316	-2,696245
108	110,70	27,65689	1,89595	-0,154081	-2,850326

Ряд 1 соответствует номинальному радиусу скважины. Ряды 2 и 3 - измеренные радиусы скважины в двух взаимно перпендикулярных направлениях. Из фиг.3 видно, что радиус скважины может быть как больше, так и меньше номинального. При этом смещения стенок могут быть как положительными, так и отрицательными. Радиусы скважины рассматриваются как полуоси полученного эллиптического сечения скважины.

В таблице 2 приведены результаты статистической обработки измерений размеров скважины в интервале от 3140 до 3160 м. Далее решаются системы уравнений (9) и (10) относительно величин λ_ф и С. Поскольку решение систем в явном виде затруднительно, то используют метод последовательных приближений. Расчет по данным о средних арифметических значениях приведен в таблице 3.

Таблица 2
Результаты измерений размеров скважины каверномером
Глубина по стволу, м	RH, мм	Rб, мм	RB, мм	ΔσR6	ΔσRв
3160	108	107,8	105,35	-0,2	-2,65
3159	108	107,7	105,05	-0,3	-2,95
3158	108	107,25	104,95	-0,75	-3,05
3157	108	107,25	104,95	-0,75	-3,05
3156	108	107,25	104,95	-0,75	-3,05
3155	108	107,6	105,55	-0,4	-2,45
3154	108	107,2	105,1	-0,8	-2,9
3153	108	107,2	105,1	-0,8	-2,9
3152	108	107,2	105,1	-0,8	-2,9
3151	108	107,3	105,1	-0,7	-2,9
3150	108	107,2	105,1	-0,8	-2,9
3149	108	107,2	105,1	-0,8	-2,9
3148	108	107,2	105,05	-0,8	-2,95
3147	108	107,2	105,15	-0,8	-2,85
3146	108	107,25	105,1	-0,75	-2,9
3145	108	107,3	105,1	-0,7	-2,9
3144	108	107,25	105,1	-0,75	-2,9
3143	108	107,35	105,15	-0,65	-2,85
3142	108	107,25	105,2	-0,75	-2,8
3141	108	107,2	105,1	-0,8	-2,9
3140	108	107,3	105,8	-0,7	-2,2
Среднее арифметическое значение	-0,693	-2,85
Среднее квадратическое отклонение	0,173	0,199

Вначале принимают максимально возможное значение λ_ф=1 и из уравнения (4) с подстановкой смещения верхней стенки скважины определяют начальное значение С:

Далее, постепенно изменяя значения λ_ф и С и подставляя их в программу, соответствующую таблице 1, добиваются совпадения вычисленных значений смещений стенок скважины с полученными выше их средними арифметическими значениями.

В таблице 3 последняя строка соответствует окончательным результатам расчета, т.е. для рассмотренного интервала среднее арифметическое значение λ_ф=0,6914, а среднее арифметическое значение модуля упругости в забойных условиях С=1867 МПа.

Таблица 3
Расчет фактических значений λФ и С
λф	С, МПа	Смещение боковой стенки	Смещение верхней стенки
1	1748		-2,840
0,7	1748	-0,613	-3,040
0,7	1800	-0,776	-2,952
0,7	1850	-0,754	-2,871
0,65	1850	-0,434	-2,900
0,65	1860	-0,434	-2,887
0,67	1860	-0,559	-2,874
0,69	1860	-0,667	-2,862
0,69	1850	-0,690	-2,877
0,69	1860	-0,687	-2,862
0,691	1860	-0,693	-2,861
0,691	1862	-0,692	-2,858
0,691	1864	-0,692	-2,855
0,691	1868	-0,690	-2,849
0,6915	1867	-0,694	-2,850
0,6914	1867	-0,693	-2,850

Аналогично, используя данные таблицы 2, вычисляются другие статистические характеристики величин λ_ф и С.

Определение фактических коэффициента бокового распора и модуля упругости горных пород позволит существенно уточнить технологические расчеты в бурении и соответственно повысить надежность запроектированных мер профилактики таких осложнений, как открытие поглощения в результате гидроразрыва пластов и прихват инструмента в результате его заклинивания в скважине, что даст существенный экономический и экологический эффект.

Способ определения упругих характеристик горной породы по данным измерений в скважине, включающий определение коэффициента Пуассона µ методом аналогий, геостатического давления р_г и давления бурового раствора р_c на рассматриваемой глубине, отличающийся тем, что в пределах заданного интервала пласта в статистически значимом количестве поперечных сечений по данным кавернометрии определяют радиальные смещения боковой и верхней стенок наклонной скважины как разности измеренных и номинального R_н радиусов скважины в двух взаимно перпендикулярных направлениях, рассчитывают средние арифметические значения, среднеквадратические отклонения и доверительные интервалы смещений стенок скважины, а затем назначают область влияния скважины с радиусом контура R_к≥50R_н, разбивают текущие радиусы в направлении от боковой и верхней стенок на n элементов толщиной h=0,10R_н, составляют две системы уравнений для боковой стенки и для верхней стенки, связывающие соответствующие смещения стенок скважины с упругими характеристиками горной породы, с геостатическим давлением и гидростатическим давлением бурового раствора и углом искривления скважины, и решают обе системы совместно методом последовательных приближений относительно модуля деформации С и фактического коэффициента бокового распора λ_ф горной породы с заданной точностью.