Способ обнаружения ошибок при приеме дискретных сообщений (варианты)

Способ обнаружения ошибок при приеме дискретных сообщений (варианты)

Иллюстрации

Показать все

Реферат

Изобретения объединены единым изобретательским замыслом, относятся к радиотехнике, а именно к способам обнаружения ошибок при приеме дискретных сообщений, и могут быть использованы при обработке дискретных сообщений в системах связи, применяющих пакетные передачи с повторным запросом.

Известен способ обнаружения ошибок при приеме дискретных сообщений, реализованный в системе радиосвязи [авторское свидетельство СССР №1688423, 1991], заключающийся в следующем. Принимают дискретные сообщения по двум независимым трактам, суммируют их и затем по данным обработки результатов сложения выявляют ошибки в принятых сообщениях. Указанное техническое решение обеспечивает требуемую вероятность обнаружения ошибок при сохранении заданного объема передаваемой информации и снижении энергетических затрат. Недостатком способа является относительно низкая вероятность обнаружения ошибок в условиях нестационарности радиоканала, вызванного флуктуациями среды распространения радиоволн.

Известен способ обнаружения ошибок при приеме дискретных сообщений, реализованный в устройстве, описанном в [Андронов И.С. и др. Передача дискретных сообщений по параллельным каналам. М.: Сов. радио, 1971. с.337-342]. Указанный способ реализует дискретное сложение при разнесенном приеме. В данном способе формируют импульсы, соответствующие переданным символам логической «единицы» и логического «нуля», суммируют их и по результатам суммирования принимают решение о наличии или отсутствии ошибок в переданном дискретном сообщении.

Недостатком способа является сложность его технической реализации, так как он требует прием дискретных сообщений по нечетному числу ветвей (от трех до пяти идентичных каналов приема и соответствующее им количество аппаратуры). Кроме того, данный способ не обеспечивает обнаружение одиночных ошибок в дискретном сообщении, что снижает помехоустойчивость радиосвязи в целом.

Наиболее близким по своей технической сущности к заявленным вариантам является способ, реализованный в устройстве обнаружения и исправления ошибок (патент РФ №2109405, опубликованный 20.04.98, бюл. №11). В ближайшем аналоге (прототипе) принимают дискретное сообщение по двум разнесенным трактам приема, демодулируют дискретные сообщения до уровня последовательности импульсов, соответствующих переданным символам логической «единицы» или логического «нуля», выполняют операцию проверки наличия ошибок в последовательности импульсов. Для чего суммируют «по модулю два» принятые по двум трактам приема последовательности импульсов. По результатам суммирования принимают решение о наличии или отсутствии ошибок в принятом дискретном сообщении. Признаком наличия ошибки является значение логической «единицы» в результате суммирования «по модулю два».

Недостатком способа-прототипа является узкая область применения из-за невозможности определения блока кодовых комбинаций, в пределах которого находится ошибка. Способ-прототип нельзя использовать при работе с блочными кодами, и соответственно, способ-прототип не может быть реализован в системах связи, применяющих пакетные передачи с повторным запросом.

Кроме того, способ-прототип предполагает использование двух идентичных трактов приема и соответствующее им количество аппаратуры, что усложняет его реализацию и процесс эксплуатации.

Целью заявленного технического решения является расширение области применения за счет разработки способов (вариантов), позволяющих точно указать границы блока кодовых комбинаций, в пределах которых содержится ошибка, что обеспечивает возможность их реализации в системах связи, применяющих пакетные передачи с повторным запросом, а также возможность использования только одного тракта приема.

В первом варианте поставленная цель достигается тем, что в известном способе обнаружения ошибок, заключающемся в том, что при приеме дискретных сообщений принимают дискретное сообщение, демодулируют его до уровня последовательности импульсов, выполняют операцию проверки наличия ошибок в последовательности импульсов, по результатам которой принимают решение о наличии или отсутствии ошибок в принятом дискретном сообщении, дискретное сообщение кода значностью I и весом W принимают по одному тракту приема. После демодуляции формируют из последовательности импульсов символьное сообщение, из которого затем формируют квадратную матрицу М размером I×I элементов и рассчитывают ее собственные значения C_i, где i=1, 2, …, I. При выполнении операции проверки из полученных собственных значений выделяют максимальное собственное значение C_max и при выполнении условия C_max не равно W, т.е. C_max≠W, делают вывод о наличии ошибки в принятом дискретном сообщении. Под значностью кода I понимают число символов в кодовой комбинации. Под весом W понимают число единиц в одной кодовой комбинации. Под блоком кодовой комбинации понимают количество одновременно обрабатываемых кодовых комбинаций при обнаружении ошибок.

Во втором варианте поставленная цель достигается тем, что в известном способе обнаружения ошибок, заключающемся в том, что принимают дискретное сообщение, демодулируют его до уровня последовательности импульсов, выполняют операцию проверки наличия ошибок в последовательности импульсов, по результатам которой принимают решение о наличии или отсутствии ошибок в принятом дискретном сообщении, дискретное сообщение кода значностью I и весом W принимают по одному тракту приема. После демодуляции формируют из последовательности импульсов символьное сообщение, из которого затем формируют квадратную матрицу М размером I×I элементов и рассчитывают собственные значения C_i, где i=1, 2, …, I. При выполнении операции проверки из полученных собственных значений выделяют максимальное собственное значение C_max и вычисляют сумму собственных значений S без учета максимального значения S=S_C-C_max, где S_C - сумма всех собственных значений. И при выполнении условия S не равно R, т.е. S≠R, где R - целое число в интервале от минус W до I-W, делают вывод о наличии ошибки в принятом дискретном сообщении.

В третьем варианте поставленная цель достигается тем, что в известном способе обнаружения ошибок, заключающемся в том, что принимают дискретное сообщение, демодулируют его до уровня последовательности импульсов, выполняют операцию проверки наличия ошибок в последовательности импульсов, по результатам которой принимают решение о наличии или отсутствии ошибок в принятом дискретном сообщении, дискретное сообщение кода значностью I и весом W принимают по одному тракту приема. После демодуляции формируют из последовательности импульсов символьное сообщение, из которого затем формируют квадратную матрицу М размером I×I элементов и рассчитывают собственные значения C_i, где i=1, 2, …, I. При выполнении операции проверки выделяют из полученных собственных значений максимальное собственное значение C_max, вычисляют сумму всех собственных значений S без учета максимального значения S=S_C-C_max, где S_C - сумма всех собственных значений, и вычисляют сумму всех собственных значений S_W без учета величины значения веса S_W=S_C-W. При выполнении условия S не равно S_W, т.е. S≠S_W, делают вывод о наличии ошибки в принятом дискретном сообщении.

В четвертом варианте поставленная цель достигается тем, что в известном способе обнаружения ошибок, заключающемся в том, что принимают дискретное сообщение, демодулируют его до уровня последовательности импульсов, выполняют операцию проверки наличия ошибок в последовательности импульсов, по результатам которой принимают решение о наличии или отсутствии ошибок в принятом дискретном сообщении, дискретное сообщение кода значностью I и весом W принимают по одному тракту приема. После демодуляции формируют из последовательности импульсов символьное сообщение, из которого затем формируют квадратную матрицу М размером I×I элементов и рассчитывают матрицу ее собственных векторов V размером I×I элементов. При выполнении операции проверки в каждом столбце матрицы V определяют число одинаковых элементов N_n, где n=1, 2, …, I. Выделяют столбец, имеющий наибольшее количество одинаковых элементов N_max, и при выполнении условия N_max меньше I, т.е. N_max<I, делают вывод о наличии ошибки в принятом дискретном сообщении.

В пятом варианте поставленная цель достигается тем, что в известном способе обнаружения ошибок, заключающемся в том, что принимают дискретное сообщение, демодулируют его до уровня последовательности импульсов, выполняют операцию проверки наличия ошибок в последовательности импульсов, по результатам которой принимают решение о наличии или отсутствии ошибок в принятом дискретном сообщении, дискретное сообщение кода значностью I и весом W, принимают по одному тракту приема. После демодуляции формируют из последовательности импульсов символьное сообщение, из которого затем формируют квадратную матрицу М размером I×I элементов. Рассчитывают матрицу ее собственных векторов V размером I×I элементов и кодовый символ Kc матрицы М. При выполнении операции проверки вычисляют модули значений элементов |V_i,i|, где i=1, 2, …, I, находящихся на диагонали матрицы V. Сравнивают их с кодовым символом Kc и при равенстве, по крайней мере, одного из значений |V_i,i| с Kc делают вывод об отсутствии ошибки в принятом дискретном сообщении. Причем матрицу собственных векторов V размером I×I элементов вычисляют по алгоритму Якоби, а кодовый символ Kc матрицы М рассчитывают по формуле .

В шестом варианте поставленная цель достигается тем, что в известном способе обнаружения ошибок, заключающемся в том, что принимают дискретное сообщение, демодулируют его до уровня последовательности импульсов, выполняют операцию проверки наличия ошибок в последовательности импульсов, по результатам которой принимают решение о наличии или отсутствии ошибок в принятом дискретном сообщении, дискретное сообщение кода значностью I и весом W принимают по одному тракту приема. После демодуляции формируют из последовательности импульсов символьное сообщение, из которого затем формируют квадратную матрицу М размером I×I элементов. Рассчитывают матрицу ее собственных векторов V размером I×I элементов и кодовый символ Kc матрицы М. А при выполнении операции проверки наличия ошибки вычисляют сумму значений элементов каждого i-го собственного вектора , где n=1, 2, …, I - количество строк матрицы собственных векторов V, a i=1, 2, …, I - количество столбцов матрицы собственных векторов V. Вычисляют произведение Р=Kc×I. Сравнивают каждую из сумм U_i с произведением Р и при равенстве, по крайней мере, одной из сумм U_i с Р делают вывод об отсутствии ошибки в принятом дискретном сообщении. Причем матрицу собственных векторов V размером I×I элементов вычисляют по алгоритму Якоби, а кодовый символ Kc матрицы M рассчитывают по формуле .

В седьмом варианте поставленная цель достигается тем, что в известном способе обнаружения ошибок, заключающемся в том, что принимают дискретное сообщение, демодулируют его до уровня последовательности импульсов, выполняют операцию проверки наличия ошибок в последовательности импульсов, по результатам которой принимают решение о наличии или отсутствии ошибок в принятом дискретном сообщении, дискретное сообщение кода значностью I и весом W принимают по одному тракту приема. После демодуляции формируют из последовательности импульсов символьное сообщение, из которого затем формируют квадратную матрицу М размером I×I элементов, рассчитывают ее собственные значения C_i, где i=1, 2, …, I, и вычисляют их модули |C_i|. При выполнении операции проверки сравнивают |C_i| с W и при равенстве, по крайней мере, одного из |C_i| с W делают вывод об отсутствии ошибки в принятом дискретном сообщении.

Благодаря новой совокупности существенных признаков в заявленных вариантах способах (вариантах) по каждому из вариантов 1-7, обеспечивается возможность определения блока кодовых комбинаций в принятом дискретном сообщении, кодированного блочным кодом со значностью I и весом W (например, код МТК №3, имеющий I=7 и W=3 [В.Григорьев. Сигналы современных зарубежных систем электросвязи. - СПб.: ВАС, 2007, с.60-62]), в пределах которых содержится ошибка, что обеспечивает возможность их реализации в системах связи, применяющих пакетные передачи с повторным запросом, а также возможность использования только одного тракта приема, и указывает на расширение области применения заявленных способов (вариантов).

Заявленные способы (варианты) поясняются чертежами, на которых показаны:

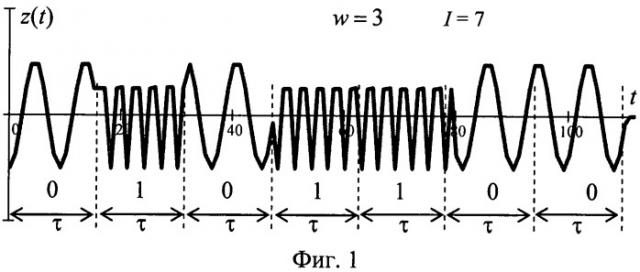
фиг.1. Временная реализация аналогового сигнала z(t) дискретного сообщения семиэлементного кода I=7 с весом W=3;

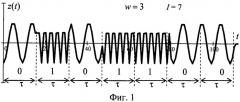
фиг.2. Временная реализация последовательности импульсов s(t) демодулированного аналогового сигнала z(t) дискретного сообщения семиэлементного кода I=7 с весом W=3 (последовательность s(t) содержит три импульса е₁, соответствующих логической «единице», и четыре импульса е₀, соответствующих логическому «нулю»);

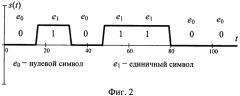
фиг.3. Символьная последовательность кодовых комбинаций демодулированного аналогового сигнала z(t);

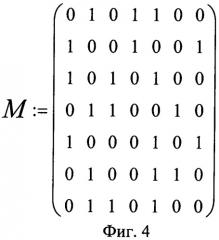
фиг.4. Квадратная матрица М размером I×I, сформированная из символьной последовательности кодовых комбинаций семиэлементного кода I=7 с весом W=3 дискретного сообщения, принятого без ошибок;

фиг.5. Квадратная матрица °М размером I×I, сформированная из символьной последовательности кодовых комбинаций семиэлементного кода I=7 с весом W=3 дискретного сообщения, принятого с одной ошибкой;

фиг.6. Собственные значения C_i матрицы М размером I×I элементов принятого без ошибок дискретного сообщения;

фиг.7. Собственные значения °C_i матрицы М размером I×I элементов принятого с ошибкой дискретного сообщения;

фиг.8. Матрица собственных векторов V размером I×I элементов для матрицы М;

фиг.9. Матрица собственных векторов °V размером I×I элементов матрицы для °М;

фиг.10. Столбец, имеющий наибольшее количество одинаковых элементов N_max в матрице V;

фиг.11. Столбец, имеющий наибольшее количество одинаковых элементов °N_max в матрице °V;

фиг.12. Модули значений элементов |V_i,i|, находящихся на диагонали матрицы собственных векторов V размером I×I;

фиг.13. Модули значений элементов |°V_i,i|, находящихся на диагонали матрицы собственных векторов °V размером I×I.

Реализация заявленных вариантов способа заключается в следующем.

Существующая проблема обнаружения ошибок при приеме дискретных сообщений по радиоканалу заключается в том, что реализация принципа сложения «по модулю два» предполагает наличие не менее двух трактов приема с однотипным набором оборудования. Между тем, разнесение трактов в условиях воздействия помех не гарантирует безошибочный прием дискретных сообщений, поэтому для борьбы с указанным явлением применяются пакетные передачи с повторным запросом. Такие передачи известны и описаны, например в [Б.Скляр. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. - М.: Издательский дом «Вильямс», 2003, с.342-344]. Следовательно, при использовании пакетных передач с повторным запросом достаточно выявить только факт наличия ошибки в блоке кодовых комбинаций, что и обеспечивается в заявляемых способах (вариантах).

В первом варианте последовательность действий над сигналом реализуется следующим образом.

Дискретное сообщение кода значностью I и весом W принимают в виде аналогового сигнала z(t) по тракту приема. Процедуры приема сигналов дискретных сообщений известны и описаны, например, в [Дж.Возенкрафт, И.Джекобс. Теоретические основы техники связи. Пер. с англ. - М.: Издат «Мир», 1969, с.216-226]. Затем принятый аналоговый сигнал z(t) демодулируют до уровня последовательности импульсов. Процедура демодуляции известна и описана, например, в [Б.Скляр. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. - М.: Издательский дом «Вильямс», 2003, с.135-138]. В качестве примера на фиг.1 показан фрагмент дискретного сообщения кодовой комбинации значностью I=7 и весом W=3 в виде аналогового сигнала z(t), у которого длительность элемента разряда равна τ. На фиг.2 показан фрагмент демодулированного аналогового сигнала z(t) дискретного сообщения кода значностью I=1 и весом W=3 в виде последовательности импульсов s(t) (3 импульса е₁, соответствующих логической «единице», и 4 импульса e₀, соответствующих логическому «нулю»).

После этого из сигнала s(t) формируют символьную последовательность кодовых комбинаций. Процесс формирования символьной последовательности известен и описан, например, в [Б.Скляр. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. - М.: Издательский дом «Вильямс», 2003, с.331-341 и Дж.Возенкрафт, И.Джекобс. Теоретические основы техники связи. Пер. с англ. - М.: Издат «Мир», 1969, с.10-30, 216-226]. В качестве примера на фиг.3 изображена символьная последовательность демодулированного сигнала z(t) дискретного сообщения кода значностью I=7 и весом W=3. На фиг.3 символьные значения сгруппированы в кодовые комбинации с порядковым номером g=1, 2, …, G, где G - общее количество принятых кодовых комбинаций. Каждая кодовая комбинация содержит количество символов, численно равное значности кода I.

Затем из поступающего потока кодовых комбинаций формируют матрицу М размером I×I элементов таким образом, что каждую строку матрицы составляют I элементов, соответствующие только одной кодовой комбинации. В результате при безошибочном приеме дискретного сообщения каждая строка матрицы М будет содержать число единиц, соответствующее весу кода W. Процесс формирования квадратных матриц известен и описан, например в [Ф.Гантмахер. Теория матриц. М.: Гос. изд-во технико-теоретической литературы, 1953, с.11-25]. В качестве примера на фиг.4 изображена квадратная матрица, сформированная из кодовых комбинаций семиэлементного кода I=7 с весом W=3 дискретного сообщения, принятого без ошибок. На фиг.5 изображена квадратная матрица °М, сформированная из кодовых комбинаций семиэлементного кода I=7 с весом W=3 дискретного сообщения, принятого с одной ошибкой. Ошибкой является наличие принятого символа логической «единицы» вместо переданного символа логического «нуля» (см. седьмой элемент первой строки матрицы °М на фиг.5). Известно, что в системах радиосвязи используют несимметричные каналы, в которых вероятность перехода сигнала, соответствующего логической «единицы» в «нуль», значительно больше вероятности перехода логического «нуля» в «единицу». Данный факт описан, например, в [В.Григорьев. Сигналы современных зарубежных систем электросвязи: Учебник. - СПб.: ВАС, 2007, с.60-62].

После этого для сформированной матрицы М размером I×I элементов рассчитывают ее собственные значения C_i, где i=1, 2, …, I. Процесс расчета собственных значений известен и описан, например, в [Сборник научных программ на Фортране. Вып.2. Матричная алгебра и линейная алгебра, Нью-Йорк, 1960-1971, пер. с англ. (США). М., Статистика, 1974, 224 с., С.187-210]. В качестве примера на фиг.6 изображены собственные значения C_i матрицы М размером I×I элементов принятого без ошибок дискретного сообщения семиэлементного кода I=7 с весом W=3. На фиг.7 изображены собственные значения °C_i матрицы М размером I×I элементов принятого с ошибкой дискретного сообщения семиэлементного кода I=7 с весом W=3.

Затем из совокупности собственных значений C_i выделяют максимальное собственное значение C_max. Процедуру выделения собственного значения C_max можно реализовать, например, путем последовательного парного сравнения собственных значений C_i друг с другом.

После этого максимальное собственное значение C_max сравнивают с числовым значением веса W=3 и при выполнении условия C_max≠W делают вывод о наличии ошибки в принятом дискретном сообщении.

Правомерность предлагаемых в заявляемом способе операций определяется следующим. В теории линейного векторного пространства спектральное разложение матрицы М предусматривает нахождение ее собственных значений C_i и собственных векторов V_i, где i=1, 2, …, I. Так, собственным вектором матрицы М является ненулевой вектор V, если он удовлетворяет равенству:

[см. Чинаев П.И., Черенков А.А., Минин Н.А., и др. Высшая математика. Специальные главы. Киев, Издательское объединение «Вища школа», 1977, 368 с. С.223-226].

Следовательно, если предположить, что один из совокупности собственных векторов V_i является единичным, то результатом его умножения на матрицу М будет некоторый вектор-столбец F, каждое из значений которого будет соответствовать сумме единиц, расположенных в соответствующих строках матрицы М. В том случае, когда матрица М формируется из кодовых комбинаций, принятых без ошибок, каждое значение вектора-столбца F будет соответствовать весу кодовой комбинации W. Тогда, согласно формуле (1), равенство будет выполняться только в том случае, если С=W. Причем согласно формуле (1), единичному вектору V будет соответствовать максимальное значение С.

В качестве примера на фиг.6 изображены собственные значения матрицы М, а на фиг.7 матрица °М. У матрицы М максимальное собственное значение C_max=3, а у матрицы °М максимальное собственное значение C_max=3,159. Следовательно, матрица М сформирована из символьной последовательности кодовых комбинаций, принятых без ошибок дискретного сообщения, а матрица °М из комбинаций, принятых с ошибкой (все расчеты в описании изобретения проводились в вычислительной среде Mathcad 11, все значения представлены в формате округления до третьего знака, собственные значения и собственные вектора рассчитывались с использованием встроенных алгоритмов вычислительной среды Mathcad 11).

Таким образом, благодаря возможности объективного сравнения максимального собственного значения C_max матрицы М с численным значением величины веса кодовой комбинации W обеспечивается возможность обнаружения ошибок в блоке кодовых комбинаций принятого дискретного сообщения, что обуславливает расширение области применения заявленного способа по варианту 1, т.е. реализуется возможность достижения указанного технического результата.

Отличие во втором варианте заключается в реализации способа проверки ошибок в символьном сообщении, а именно. После выделения максимального собственного значения C_max вычисляют сумму всех собственных значений без величины C_max. Процедуру вычисления суммы можно осуществить по формуле

где S_C - сумма всех собственных значений, которая рассчитывается по формуле

Затем проверяют выполнение условия S≠R, где R - целое число в интервале от минус W до I-W, и делают вывод о наличии ошибки в принятом дискретном сообщении.

Правомерность предлагаемых в заявляемом способе операций определяется следующим. Известно, что сумма собственных значений матрицы ровна сумме значений элементов матрицы, расположенных на ее главной диагонали. Элементы, расположенные на главной диагонали квадратной матрицы порядка I, определяются как a_i,i, где i=1, …, I; а - элемент матрицы см. [Ф.Гантмахер. Теория матриц. М.: Гос. изд-во технико-теоретической литературы, 1953, с.11-25]. Диапазон изменения R от минус W до I-W определяется тем, что сумма собственных значений зависит от числа единиц на диагонали матрицы М. Максимальное число единиц равно I, а минимальное ноль - см. [Ф.Гантмахер. Теория матриц. М.: Гос. изд-во технико-теоретической литературы, 1953, с.73-79]. Тогда с учетом формулы (2) получаем диапазон изменения R.

В качестве примера вычислим сумму S для собственных значений C_i матрицы М (см. фиг.6) по формуле (2). В итоге получим S=0, т.е. значение S является целым числом. Следовательно, символьная последовательность блока кодовых комбинаций, из элементов которой сформирована матрица М, не содержит ошибок. Теперь вычислим сумму S для собственных значений °C_i матрицы °М (см. фиг.7) по формуле (2). Получим S=-0,159, т.е. значение S не является целым числом. Следовательно, символьная последовательность блока кодовых комбинаций, из элементов которой сформирована матрица °М, содержит ошибку.

Таким образом, благодаря возможности объективного сравнения суммы собственных значений без максимального собственного значения с некоторым целым числом R=-W, …, I-W; где W есть вес, а I есть значность кода, обеспечивается возможность обнаружения ошибок в блоке кодовых комбинаций принятого дискретного сообщения, что обуславливает расширение области применения заявленного способа по варианту 2, т.е. реализуется возможность достижения указанного технического результата.

Отличие в варианте 3 заключается в реализации способа проверки ошибок в символьном сообщении, а именно. После выделения максимального собственного значения C_max вычисляют сумму собственных значений S_C. Сумму S_C можно вычислить по формуле (3).

Затем вычисляют сумму собственных значений без максимального собственного значения S по формуле (2) и вычисляют сумму собственных значений S_W без учета величины значения веса W по формуле:

Решение о наличии ошибки в принятом дискретном сообщении принимают, если результаты вычисления S и S_W не равны между собой.

Правомерность предлагаемых в заявляемом способе операций определяется следующим. В случае, когда квадратная матрица содержит строки, сумма элементов которых имеет одинаковое значение (одинаковый вес), то одно из собственных значений такой матрицы будет иметь численную величину, равную численному значению веса [см. Чинаев П.И., Черенков А.А., Минин Н.А. и др. Высшая математика. Специальные главы. Киев, Издательское объединение «Вища школа», 1977, 368 с., с.223-226]. Следовательно, в этом случае разность суммы собственных значений и максимального собственного значения, а также разность суммы собственных значений и численной величины веса будут иметь одинаковые значения.

В качестве примера вычислим по формуле (4) и (2), с учетом формулы (3), значение суммы S_W и S для собственных значений C_i (см. фиг.6) матрицы М (см. фиг.4) и значение суммы °S_W и °S для собственных значений °C_i (см. фиг.7) матрицы °М (см. фиг.5). В итоге получим для первого случая S_W=0 и S=0, а для второго случая °S_W=-0,159 и °S=0. Результаты парного сравнения S_W и S, и °S_W и °S показывают, что во втором случае °S_W≠°S, т.е. символьная последовательность блока кодовых комбинаций, из элементов которой сформирована матрица °М, содержит ошибку.

Таким образом, благодаря возможности объективного сравнения разности суммы собственных значений и максимального собственного значения, а также разности суммы собственных значений и численной величины веса обеспечивается возможность обнаружения ошибок в блоке блока кодовых комбинаций принятого дискретного сообщения, что обуславливает расширение области применения заявленного способа по варианту 3, т.е. реализуется возможность достижения указанного технического результата.

Отличие в варианте 4 заключается в дополнительном расчете матрицы собственных векторов V размером I×I элементов и реализации способа проверки ошибок в символьном сообщении, а именно. В каждом столбце матрицы V определяют число одинаковых элементов N_n, где n=1, 2, …, I. Операцию определения числа одинаковых элементов можно реализовать, например, путем парного сравнения элементов друг с другом. Процесс расчета собственных векторов известен и описан, например, в [Сборник научных программ на Фортране. Вып.2. Матричная алгебра и линейная алгебра. Нью-Йорк, 1960-1971, пер. с англ. (США). М., Статистика, 1974, 224 с., С.187-210]. Так как матрицы собственных векторов третьего и более высоких порядков могут содержать комплексные значения, то в алгоритме Якоби предусмотрена нормировка всех элементов матрицы на величину , где I - размерность матрицы (количество элементов кодовой комбинации). Алгоритм Якоби, используемый для расчета собственных векторов, известен и описан, например, в [Сборник научных программ на Фортране. Вып.2. Матричная алгебра и линейная алгебра. Нью-Йорк, 1960-1971, пер. с англ. (США). М., Статистика, 1974, 224 с., С.187-210].

Правомерность предлагаемых в заявляемом способе операций определяется следующим. В соответствии с формулой (1) в качестве собственного вектора V матрицы М может выступать единичный вектор в том случае, если вес каждой строки матрицы М будет иметь одинаковое числовое значение. Такая ситуация возможна только в том случае, если матрица М будет сформирована из кодовых комбинаций принятого без ошибок дискретного сообщения.

Затем выделяют столбец, имеющий наибольшее количество одинаковых элементов N_max. Операцию выделения можно реализовать также путем парного сравнения элементов друг с другом. Решение о наличии ошибки в принятом дискретном сообщении при выполнении условия N_max<I, которое можно реализовать путем парного сравнения указанных значений.

В качестве примера на фиг.10 изображена матрица собственных векторов V размером I×I элементов матрицы М. На фиг.11 изображена матрица собственных векторов °V размером I×I элементов матрицы °М. Указанные матрицы М и °М сформированы из кодовых комбинаций кода с параметрами I=7 и весом W=3. В матрице V (см. фиг.8) наибольшее число одинаковых элементов имеет первый столбец N_max=7 (см. фиг.10). В матрице °V (см. фиг.9) все столбцы имеют разные элементы, поэтому °N_max=1 (см. фиг.11). Так как N_max=I, a °N_max<I, то делаем вывод, что матрица М не содержит ошибки, а матрица °М содержит ошибку.

Таким образом, благодаря возможности объективного сравнения наибольшего количества одинаковых элементов N_max в столбце матрицы собственных векторов с количеством элементов I в матрице символьного сообщения М, обеспечивается возможность обнаружения ошибок в блоке кодовых комбинаций принятого дискретного сообщения, что обуславливает расширение области применения заявленного способа по варианту 4, т.е. реализуется возможность достижения указанного технического результата.

Отличие в варианте 5 заключается в дополнительном расчете матрицы собственных векторов V размером I×I элементов и кодового символа Kc матрицы М, который при использовании алгоритма Якоби при расчете матрицы V, вычисляется по формуле

где I - количество элементов кодового сообщения (количество элементов в матрице символьного сообщения М).

Кроме того, вариант 5 отличается в реализации способа проверки ошибок в символьном сообщении, а именно. Для матрицы V вычисляют модули значений ее элементов |V_i,i|, где i=1, 2, …, I, находящихся на диагонали матрицы. Процедура вычисления модуля числа известна как

и описана, например [Гусев В.А., Мордкович А.Г. Математика: Справ. Материалы: Кн. Для учащихся. - М.: Просвещение, 1988, с.36]. В формуле (6) А в общем случае произвольное число.

Затем значения модулей элементов матрицы |V_i,i| сравнивают с кодовым символом Kc, рассчитанным согласно формуле (5). Решение об отсутствии ошибки в принятом дискретном сообщении делают при равенстве, по крайней мере, одного из значений |V_i,i| с Kc. Указанные процедуры сравнения можно реализовать, например, путем парного перебора.

Правомерность предлагаемых в заявляемом способе операций определяется следующим. В сформированных матрицах V и °V элементы каждого столбца являются элементами соответствующего собственного вектора. Следовательно, у единичного собственного вектора все элементы будут одинаковы (при использовании для расчета алгоритма Якоби они равны ). Поэтому, для установления факта наличия единичного вектора в матрице собственных векторов достаточно вычислить значение модуля любого из его элементов.

В качестве примера вычислим модули значений |V_i,i| (см. фиг.12) для матрицы собственных векторов V (см. фиг.8) и модули значений |°V_i,i| (см. фиг.13) для матрицы собственных векторов °V (см. фиг.9). Рассчитаем значение Kc по формуле (5). Получим Kc=0,378. Сравним Kc со значениями |V_i,i| и |°V_i,i|. В |V_i,i| значения |V_1,1|=0,378 и |V_3,3|=0,378 совпадают с Kc. В то же время ни одно из значений |°V_i,i| с Kc не совпадают. Следовательно, делаем вывод, что матрица М не содержит ошибки, а матрица °М содержит ошибку.

Таким образом, благодаря возможности объективного сравнения модулей значений |V_i,i|, находящихся на диагонали матрицы собственных векторов V, со значением кодового символа Kc, представляющего обратную величину квадратного корня из значения длины кодовой комбинации, обеспечивается возможность обнаружения ошибок в блоке кодовых комбинаций принятого дискретного сообщения, что обуславливает расширение области применения заявленного способа по варианту 5, т.е. реализуется возможность достижения указанного технического результата.

Отличие в варианте 6 заключается в дополнительном расчете матрицы собственных векторов V размером I×I элементов и кодового символа Kc матрицы М, который при использовании алгоритма Якоби при расчете матрицы V вычисляется по формуле (5). Кроме того, вариант 6 отличается в реализации способа проверки ошибок в символьном сообщении, а именно. Вычисляют сумму значений элементов каждого i -го собственного вектора по формуле

где n=1, 2, …, I - количество строк матрицы собственных векторов V; i=1, 2, …, I - количество столбцов матрицы собственных векторов V.

В матрице собственных векторов V соответствующий собственный вектор представляет совокупность элементов, расположенных в столбце матрицы V - см. [Ф.Гантмахер. Теория матриц. М.: Гос. изд-во технико-теоретической литературы. 1953, с.63-66].

Затем вычисляют произведение Р по формуле

где Kc - кодовый символ матрицы М, рассчитываемый по формуле (5); I - длина кодовой комбинации.

После этого сравнивают каждую из сумм U_i, рассчитанную согласно формуле (7), с произведением Р, рассчитанным согласно формуле (8).

Решение об отсутствии ошибки в блоке кодовых комбинаций принятого дискретного сообщения делают при равенстве, по крайней мере, одной из суммы U_i с Р. Процедуру сравнения можно реализовать, например, путем парного перебора значений U_i и Р.

Правомерность предлагаемых в заявляемом способе операций определяется следующим. Сумма элементов единичного вектора матрицы собственных векторов, рассчитанных по алгоритму Якоби, определяется как , где I - порядок матрицы V, который определяется размерностью кода. Следовательно, если матрица собственных векторов V соответствует матрице М, сформированной из кодовых комбинаций, принятых без ошибки, то сумма элементов единичного собственного вектора будет численно равна произведению, вычисленному по формуле (8).

В качестве примера вычислим значения сумм U_i элементов собственных векторов матрицы V (см. фиг.8). Сумма элементов первого вектора U₁=2,646; второго U₂=-0,459; третьего U₃=-0,378; четвертого U₄=-0,268+j0,24; пятого U₅=-0,268-j0,24; шестого U₆=-0,277; седьмого U₇=-0,277. Затем вычислим значения сумм °U_i элементов собственных векторов матрицы °V (см. фиг.9). Сумма элементов первого вектора °U₁=2,632; второго °U₂=0,678; третьего °U₃=-0,248; четвертого °U₄=0,064+j0,169; пятого °U₅=0,064-j0,169; шестого °U₆=-0,171-j0,038; седьмого °U₇=-0,171+j0,038. Здесь j - знак мнимой части. По формуле (7) рассчитаем произведение Р=2,646. Вычислим по формуле (8) произведение Р=2,646. Результаты сравнения полученного значения Р со значениями сумм U_i и °U_i показывает, что U₁=P. Следовательно, делаем вывод, что матрица М не содержит ошибки, а матрица °М содержит ошибку.

Таким образом, благодаря воз