Способы и устройство для интегрирования систематического прореживания данных в основанный на генетическом алгоритме выбор подмножества признаков

Способы и устройство для интегрирования систематического прореживания данных в основанный на генетическом алгоритме выбор подмножества признаков

Иллюстрации

Показать все

Реферат

Областью техники заявки являются способы и устройство для интегрирования систематического прореживания данных в основанные на генетических алгоритмах системы выбора подмножества признаков для извлечения данных, уменьшения ложно положительных результатов (FPR), компьютеризированного обнаружения (CAD), компьютеризированной диагностики (CADx) и искусственного интеллекта.

Алгоритмы CAD были разработаны, чтобы автоматически распознавать важные с медицинской точки зрения анатомические признаки, такие как подозрительные поражения, по снимкам сканирования многослоевой компьютерной томографии (MSCT), и, тем самым, чтобы давать дополнительное мнение для использования рентгенологом. Эти алгоритмы помогают в раннем обнаружении раков, ведущем к повышенным коэффициентам выживаемости. Например, рак легких является одним из наиболее распространенных смертельных заболеваний, со 162460 смертельными исходами, обусловленными раком легких, ожидаемыми в 2006 году в Соединенных Штатах (American Cancer Society, «Cancer Facts & Figures 2006» («Данные по раку и диаграммы 2006 года»), Atlanta 2006) и 5-летней выживаемостью для пациентов с раком легких всего лишь около 15%, несмотря на усовершенствования в хирургической технике и терапии. Однако выживаемость значительно улучшается до приблизительно 50% для случаев, обнаруженных, когда заболевание еще локализовано. Таким образом, раннее обнаружение и диагностирование подозрительных поражений предусматривает раннее вмешательство и может приводить к лучшим прогнозам и коэффициентам выживаемости.

Известно, что использование технологий машинного самообучения в качестве этапа постобработки должно устранять ложно положительные структуры, которые ошибочно распознаются в качестве легочных включений алгоритмом CAD. Моуса и Хан использовали машины опорных векторов (SVM) для отсортировывания легочных включений от невключений (W.A.H. Mousa и M.A.U. Khan, Lung nodule classification utilizing support vector machines (Классификация легочных включений с использованием машин опорных векторов), presented at Int'l Conf. On Image Processing, 2002).

Ге и другие предложили линейный дискриминантный классификатор, основанный на 3-мерных признаках (Ge et al., Computer aided detection of lung nodules: false positive reduction using a 3D gradient field method (Компьютеризированное обнаружение легочных включений: уменьшение ложно положительных результатов с использованием способа 3-мерного градиентного поля), presented at Medical Imaging 2004: Image Processing, San Diego 2004).

Сузуки и другие предложили искусственную нейронную сеть массового обучения (MTANN), которая способна к непосредственному оперированию данными изображений и не требует извлечения признаков (K. Suzuki et al., Massive training artificial neural network (MTANN) for reduction of false positives in computerized detection of lung nodules in low-dose computed tomography (Искусственная нейронная сеть массового обучения (MTANN) для уменьшения ложно положительных результатов при компьютеризованном обнаружении легочных включений в компьютерной томографии с низкой дозой), 30 MED. PHYSICS 1602-17, 2003). Они пришли к выводу, что для FPR скорее могло бы быть полезным сочетание MTANN и основанного на правилах линейного дискриминантного классификатора, чем MTANN в одиночку. Большинство существующих работ по FPR следуют одной и той же методологии для контролируемого обучения: начиная со сбора данных с наземным контролем данных, классификатор обучается данными с использованием набора признаков (вычисленных из изображений), которые один или более пользователей считают надлежащими.

Несмотря на то, что последние успехи в MSCT дают возможность обнаружения рака, такого как рак легких, печени или молочной железы, на более ранней стадии, чем раньше, эти способы также имеют следствием гигантский объем данных, которые должны интерпретироваться рентгенологами, затратную и отнимающую много времени процедуру. Алгоритмы CAD обладают высокой чувствительностью, однако ни один из них не работает с безупречной точностью (то есть не способен обнаруживать все и только те структуры, которые являются истинными легочными включениями). Некоторые не относящиеся к включениям структуры (например, кровеносные сосуды) часто ошибочно помечаются как включения. Поскольку практикующие врачи, такие как рентгенолог, должны обследовать каждую распознанную структуру, крайне желательно устранить как можно больше ложно положительных результатов (FP) наряду с сохранением истинно положительных результатов (TP), то есть включений, для того, чтобы избежать утомительной работы и ошибок, вызванных ненужными обследованиями ложно положительных результатов. Это известно как уменьшение ложно положительных результатов (FPR). В отличие от других классификационных задач, которые нацелены на сокращение суммарного количества ошибочно классифицированных прецедентов, здесь цель состоит в том, чтобы устранить как можно больше FP (максимизация специфичности) при ограничении, что все TP должны сохраняться (сохранение чувствительности в 100%).

Хотя системы уменьшения ложно положительных результатов были описаны, цель таких систем, которой является максимальная специфичность наряду с сохранением 100% чувствительности, остается труднодостижимой.

Вариант осуществления изобретения предлагает способ улучшения точности классификации и уменьшения ложно положительных результатов при извлечении данных, компьютеризованном обнаружении, компьютеризованной диагностике и искусственном интеллекте. Способ включает в себя выбор набора данных обучения из набора обучающих прецедентов с использованием систематического прореживания данных. Способ также включает в себя создание классификатора на основании набора данных обучения с использованием способа классификации, при этом способ систематического прореживания данных и способ классификации создают классификатор, тем самым подавляя ложно положительные результаты и улучшая точность классификации.

В зависимом варианте осуществления классификатор выбирается из группы, состоящей из машины опорных векторов, нейронных сетей и деревьев решений.

Еще один вариант осуществления дополнительно включает в себя оценку классификатора, созданного посредством способа классификации на основании набора данных обучения, с использованием набора тестирования.

В еще одном варианте осуществления выбор набора данных обучения дополнительно включает в себя удаление из набора данных обучения ложных включений, которые образуют связи Томека с истинными включениями, до тех пор, пока не будет удовлетворено пороговое значение. В зависимом варианте осуществления пороговое значение определяется относительно коэффициента сокращения, x, из условия, чтобы количество ложных включений, оставшихся в наборе данных обучения после систематического прореживания данных, было не большим, чем взятое x раз количество истинных включений в наборе данных обучения.

В зависимом варианте осуществления способ включает в себя проверку достоверности классификатора с помощью набора прецедентов тестирования или его подмножества.

Также предложен генетический алгоритм, который, когда выполняется, реализует любой из вышеприведенных способов. В зависимом варианте осуществления генетическим алгоритмом является алгоритм CHC (L.J. Eshelman, The CHC Adaptive Search Algorithm: How to Have Safe Search When Engaging in Nontraditional Genetic Recombination (Алгоритм адаптивного поиска CHC: как получать надежный поиск при выполнении нетрадиционной генетической рекомбинации), in FOUNDATIONS OF GENETIC ALGORITHMS 265-83, G.J.E. Rawlines, ed. 1991).

Также предложен способ выбора признаков из пула признаков с использованием вышеупомянутого генетического алгоритма, способ содержит этапы: предоставления каждого из первого генетического алгоритма и второго генетического алгоритма согласно вышеприведенным способам, при этом первый генетический алгоритм используют для определения наилучшего размера набора признаков; и фиксации размера набора признаков и использования второго генетического алгоритма для выбора признаков. В зависимом варианте осуществления, при предоставлении первого генетического алгоритма, способ дополнительно содержит анализ результатов с использованием, по меньшей мере, одного из: количества вхождений хромосом, представляющих разные размеры подмножеств признаков, и количества средних ошибок. В дополнительном варианте осуществления «количество средних ошибок» является количеством ошибочно классифицированных легочных включений, полученным классификатором на основании этих хромосом.

Также предложен машиночитаемый носитель, который, когда приводится в исполнение, реализует любой из вышеприведенных способов.

Также предложено изделие, которое является устройством формирования изображений или устройством уменьшения ложно положительных результатов, при этом устройство является компьютером, который запрограммирован для анализа данных изображения посредством реализации любого из вышеприведенных способов.

В зависимом варианте осуществления в изделии, приведенном выше, устройство формирования изображений выбрано из группы, состоящей из: компьютерной томографии (CT), компьютерной аксиальной томографии (CAT), многослоевой компьютерной томографии (MSCT), послойного рентгеновского исследования, ультразвука, отображения магнитного резонанса (MRI), магнитно-резонансной томографии (MRT), ядерного магнитного резонанса (NMR), рентгенографии, микроскопии, флуороскопии, томографии и цифрового формирования изображения. В дополнительном варианте осуществления изделия, приведенного выше, изделием является система CAD легочных включений.

Фиг.1 - изображение выходных данных CAD ультразвукового снимка сканирования грудной клетки с одним поражением, обнаруженным и очерченным.

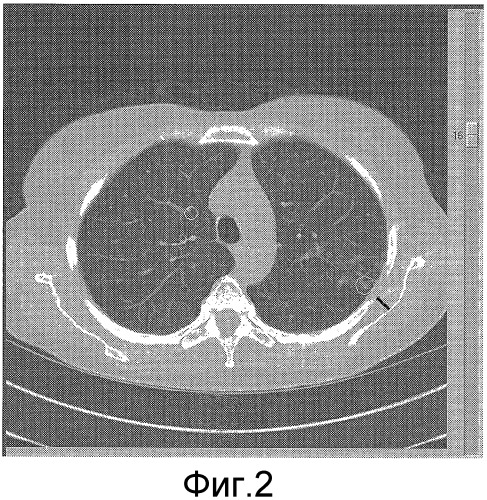
Фиг.2 - выходные данные CAD снимка сканирования CT легких с двумя обнаруженными распознанными поражениями.

Фиг.3 - схема основанного на генетическом алгоритме выбора подмножества признаков.

Фиг.4 - схема последовательности операций уменьшения ложно положительных результатов с использованием подмножества наилучших признаков, выбранного с использованием подмножества наилучших признаков, выбранных на фиг.3.

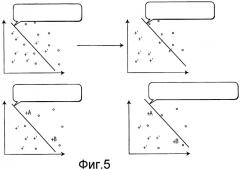
Фиг.5 показывает результат работы способа систематического сокращения для удаления ложно положительных результатов из набора данных обучения.

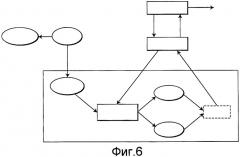
Фиг.6 - схема, изображающая интегрирование систематического прореживания данных (систематического сокращения) в последовательность операций выбора подмножества признаков GA.

Фиг.7 - график, показывающий качество функционирования генетических алгоритмов, включающих в себя случайное сокращение, систематическое прореживание данных (коэффициент сокращения 2) и систематическое прореживание данных (коэффициент сокращения 3) для подмножеств признаков с размером 5.

Фиг.8 - график, показывающий качество функционирования генетических алгоритмов, включающих в себя случайное сокращение, систематическое прореживание данных (коэффициент сокращения 2) и систематическое прореживание данных (коэффициент сокращения 3) для подмножеств признаков с размером 6.

Фиг.9 - график, показывающий качество функционирования генетических алгоритмов, включающих в себя случайное сокращение, систематическое прореживание данных (коэффициент сокращения 2) и систематическое прореживание данных (коэффициент сокращения 3) для подмножеств признаков с размером 7.

Фиг.10 - график, показывающий качество функционирования генетических алгоритмов, включающих в себя случайное сокращение, систематическое прореживание данных (коэффициент сокращения 2) и систематическое прореживание данных (коэффициент сокращения 3) для подмножеств признаков с размером 8.

Фиг.11 - график, показывающий качество функционирования генетических алгоритмов, включающих в себя случайное сокращение, систематическое прореживание данных (коэффициент сокращения 2) и систематическое прореживание данных (коэффициент сокращения 3) для подмножеств признаков с размером 9.

Фиг.12 - график, показывающий качество функционирования генетических алгоритмов, включающих в себя случайное сокращение, систематическое прореживание данных (коэффициент сокращения 2) и систематическое прореживание данных (коэффициент сокращения 3) для подмножеств признаков с размером 10.

Фиг.13 - график, показывающий качество функционирования генетических алгоритмов, включающих в себя случайное сокращение, систематическое прореживание данных (коэффициент сокращения 2) и систематическое прореживание данных (коэффициент сокращения 3) для подмножеств признаков с размером 11.

Фиг.14 - график, показывающий качество функционирования генетических алгоритмов, включающих в себя случайное сокращение, систематическое прореживание данных (коэффициент сокращения 2) и систематическое прореживание данных (коэффициент сокращения 3) для подмножеств признаков с размером 12.

Соответственно цель настоящего изобретения состоит в том, чтобы интегрировать систематическое прореживание данных в оценку подмножеств признаков-кандидатов в генетическом алгоритме.

Машины опорных векторов (SVM) являются относительно новым инструментальным средством для машинного самообучения (B.E. Boser, I. Guyon и V. Vapnik, A training algorithm for optimal margin classifiers (Алгоритм обучения для классификаторов с оптимальными границами), presented at 5^th Annual ACM Workshop on Computational Learning Theory, Pittsburgh, 1992). SVM обрели растущую популярность, начиная с конца 1990-ых (V.N. VAPNIK, THE NATURE OF STATISTICAL LEARNING THEORY (1995); V.N. VAPNIK, STATISTICAL LEARNING THEORY, 1998). Машины опорных векторов в настоящее время находятся в числе наилучших исполнителей классификационных задач, простирающихся от текстовых до геномных данных, однако некоторое количество проблем остается, как описано в материалах настоящей заявки.

SVM справляются с задачей классификации объектов на один из двух классов и подразумевают, что некоторые примеры уже были классифицированы. Цель этого типа контролируемого машинного самообучения состоит в том, чтобы предложить функцию, которая «правильно» классифицирует новый объект. Теория SVM может быть формализована, как изложено ниже: для набора {x _i , y _i} размера m данных обучения каждая информационная точка описана вектором признаков x _i ∈ R ^d и априорным знанием, что каждый x _i принадлежит к одному из классов y _i ∈ {-1,1} (i=1, ..., m). При заданной новой информационной точке x цель теории SVM состоит в том, чтобы определить функцию f из условия, чтобы {x, f(x)} была в некотором смысле подобной заданным данным обучения. Допустим, что можно найти гиперплоскость w∙x+b=0 (где точка обозначает скалярное произведение), такую, что все положительные примеры (y=1) лежат по одну сторону плоскости, а отрицательные примеры (y=-1) лежат по другую сторону, то есть

w∙x _i +b≥+1, если y _i=1,

w∙x _i +b≤-1, если y _i=-1.

В этом случае набор данных обучения является линейно сепарабельным. При заданной новой информационной точке x вычисляется w∙x+b, и знак значения сообщает, является ли x положительным или отрицательным примером. Другими словами, функция f(x)=sgn(w∙x+b) определяет классификацию любого нового вектора x.

В большинстве случаев невозможно найти гиперплоскость, которая будет четко разделять положительные и отрицательные примеры. SVM отображает исходные векторы признаков в пространство (обычно) большей размерности, где может быть найдена такая гиперплоскость:

Φ:x → φ(x).

Это отображение Ф названо кернфункцией. Есть много гиперплоскостей, которые могут разделять набор данных. Гиперплоскость выбирается из условия, чтобы минимальное расстояние векторов данных обучения (то есть нормальное расстояние до гиперплоскости) было максимальным. Векторы с этим минимальным расстоянием от гиперплоскости называются опорными (вспомогательными) векторами. Набор опорных векторов определяет разделяющую гиперплоскость. Другие векторы могут отбрасываться без изменения решения, а если удален любой из опорных векторов, гиперплоскость будет изменяться. Нахождение этой гиперплоскости, таким образом, является оптимизационной задачей.

На поверхности отображение в пространство большей размерности может вызывать вычислительные проблемы. Однако теория SVM показывает, что можно выбирать кернфункции так, чтобы результирующая функция f была привлекательной с вычислительной точки зрения.

Слово «классификатор», в качестве используемого в материалах настоящей заявки, описывает любой тип способа или устройства, способных к предсказанию, к какой группе или категории принадлежит объект. Это определение включает в себя, но не в качестве ограничения, инструментарий и технологии извлечения данных, такие как машины опорных векторов, нейронные сети и деревья решений.

Термин «способ классификации», в качестве используемого в материалах настоящей заявки, описывает любое средство создания классификатора. Это определение включает в себя, но не в качестве ограничения, инструментарий и технологии, такие как алгоритм Бозера и других для создания SVM, C4.5, J4.8 и метод APRIORI (B.E. Boser, I. Guyon и V. Vapnik, A training algorithm for optimal margin classifiers (Алгоритм обучения для классификаторов с оптимальными границами), presented at 5^th Annual ACM Workshop on Computational Learning Theory, Pittsburgh, 1992).

Вариант осуществления изобретения, приведенный в материалах настоящей заявки, является блоком основанного на машинном самообучении FPR, имеющим три основных компонента обработки: выделение признаков, управляемый SVM и основанный на GA выбор подмножества признаков, и SVM-классификатор. Блок выделения признаков вычисляет несколько 2-мерных и 3-мерных признаков из снимков сканирования CT для использования при проведении различий между истинными включениями и невключениями. Эти признаки составляют пул признаков для этапа выбора подмножества признаков, который выполняется только на фазе проектирования системы. Как только было выбрано оптимальное подмножество признаков и классификатор, построенный из них, система состоит только из выделения признаков и классификатора. Вариант осуществления изобретения использует машину опорных векторов вследствие ее превосходных эксплуатационных качеств для различных классификационных задач, в том числе поддержки медицинских решений. Другие классификаторы, такие как нейронные сети, также могут использоваться.

Для недопущения излишних вычислений и чрезмерного приближения, и чтобы обеспечить достоверный классификатор, подмножество признаков выбирается с использованием генетических алгоритмов (GA). Оберточный подход включает в себя алгоритм выбора признаков, связанный с классификатором для формирования критериев выбора (R. Kohavi и G.H. John, The Wrapper Approach (Оберточный подход), 97 ARTIFICIAL INTELLIGENCE 273-324, 1997). Одним из возможных сочетаний алгоритмов классификатора/выбора признаков, которое используется, является SVM и GA, названное CHC (L.J. Eshelman, The CHC Adaptive Search Algorithm: How to Have Safe Search When Engaging in Nontraditional Genetic Recombination (Алгоритм адаптивного поиска CHC: как получать надежный поиск при выполнении нетрадиционной генетической рекомбинации), in FOUNDATIONS OF GENETIC ALGORITHMS 265-83, G.J.E. Rawlines, ed. 1991). CHC желателен вследствие его устойчивой стратегии поиска для широкого класса задач. Способ выбора признаков способен автоматически определять оптимальный размер и набор таких признаков.

Вообще, способ в материалах настоящей заявки включает в себя создание некоторого количества «хромосом», которые состоят из многочисленных «генов» с каждым геном, представляющим выбранный признак (D. Schaffer et al., A Genetic Algorithm Approach for Discovering Diagnostic Patterns in Molecular Measurement Data (Подход генетического алгоритма для нахождения схем диагностики в данных молекулярных измерений), PROCEEDINGS OF THE 2005 IEEE SYMPOSIUM ON COMPUTATIONAL INTELLIGENCE IN BIOINFORMATICS AND COMPUTATIONAL BIOLOGY 1, 2005).

Набор признаков, представленный хромосомой, используется для обучения SVM с использованием порции данных обучения, соответствующей подмножеству признаков. Пригодность хромосомы оценивается согласно тому, насколько хорошо результирующая SVM работает на данных тестирования. В одном из вариантов осуществления функция иерархической пригодности, основанная на соотношении сохранения истинных включений и исключения ложно положительных результатов классификации SVM, выполняется на наборе тестирования. В альтернативных вариантах осуществления можно разрабатывать и использовать разные функции пригодности.

В начале этой последовательности операций популяция хромосом формируется случайным выбором признаков для формирования хромосом. Алгоритм затем многократно отыскивает те хромосомы, которые имеют более высокие значения продуктивности (более высокую пригодность). В каждом поколении GA оценивает пригодность каждой хромосомы в популяции и, посредством двух основных эволюционных методов, мутации и скрещивания, создает новые хромосомы из более пригодных. Гены, которые находятся в хороших хромосомах, должны наиболее вероятно сохраняться для следующего поколения, а таковые с плохой продуктивностью должны наиболее вероятно отбрасываться. В итоге, набор признаков с высокой продуктивностью обнаруживается благодаря этому процессу естественного отбора.

Цель изобретения состоит в том, чтобы улучшить эксплуатационные качества генетического алгоритма интегрированием систематического прореживания данных в оценку подмножеств признаков-кандидатов. В этом варианте осуществления систематическое прореживание данных используется для выбора набора данных обучения из набора обучающих прецедентов.

Для каждого набора подмножества признаков-кандидатов выбирается набор данных обучения из набора обучающих прецедентов. Пограничные с ложно положительными прецеденты удаляются из набора данных обучения. Набор данных обучения затем используется для создания классификатора, который используется для оценки пригодности подмножества признаков-кандидатов в качестве части генетического алгоритма.

В еще одном варианте осуществления пограничные с ложно положительными результаты могут распознаваться посредством концепции связей Томека (G.E.A.P.A. Batista, A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data (Изучения поведения нескольких способов для балансировки данных обучения машинного самообучения), 6 SIGKDD EXPLORATIONS 20-29, 2004). При заданном прецеденте A истинного включения и прецеденте B ложного включения, пусть d(A, B) будет расстоянием между A и B. Пара (A, B) названа связью Томека, если нет примера C (который может быть истинным включением или ложным включением), такого, что d(A, C)<d(A, B) или d(B, C)<d(A, B). Если A и B формируют связь Томека, то A или B являются шумовыми, либо A и B являются пограничными. Когда связи Томека используются в этом сценарии уменьшения ложно положительных результатов, только ложно положительный прецедент B удаляется в качестве способа сокращения. Фиг.5 показывает, как этот способ сокращения работает для сохранения большего количества истинных включений.

В дополнительном варианте осуществления некоторое количество удаленных ложно положительных прецедентов может уточняться, чтобы лучше добиваться требуемой специфичности и чувствительности. Это достигается благодаря использованию коэффициента x сокращения. Коэффициент (x) сокращения определен в качестве: количества ложных включений, оставшихся в наборе данных обучения (после удаления пограничных с ложно положительными прецедентов), которое является не большим, чем взятое x раз количество истинных включений в наборе данных обучения. Этот коэффициент может настраиваться. Уменьшение x благоприятствует большей чувствительности (меньшей специфичности). Увеличение x благоприятствует меньшей чувствительности (большей специфичности). Для уменьшения ложно положительных результатов типичной целью является наибольший коэффициент (значение x), который доводит до максимума специфичность наряду с сохранением 100% чувствительности.

Были проведены примеры для проверки действительности изобретения. Первый пример сравнивал три способа сокращения: случайное сокращение, систематическое сокращение (коэффициент сокращения 2) и систематическое сокращение (коэффициент сокращения 3).

Набор данных сначала разделялся на набор данных обучения и набор проверки достоверности.

	Набор данных обучения	Набор проверки достоверности
Истинные включения	67	22
Ложные включения	483	160

Способы разделения данных использовали следующие схемы. Для случайного сокращения:

	Обучение	Тестирование	Всего
Истинные включенияЛожные включения	5050	17433	67483

Для систематического сокращения (обоих коэффициентов 2 и 3):

	Обучение	Тестирование	Всего
Истинные включенияЛожные включения	50360	17123	67483

Для этого примера оценивались размеры от 5 до 12 подмножества признаков, которые определялись ранее в качестве наилучших размеров подмножества признаков из пула признаков в 23 признака. Для каждого размера проводились осуществления в следующей таблице:

	Сокращение в пределах GA
	Случайное	Коэффициент 2	Коэффициент 3
Начальное значение 0	Наилучшее подмножество признаков	...	Наилучшее подмножество признаков
Начальное значение 1	Наилучшее подмножество признаков	...	Наилучшее подмножество признаков
Начальное значение 2	Наилучшее подмножество признаков		Наилучшее подмножество признаков
Начальное значение 3	...		...
Начальное значение 4	...		...
Начальное значение 5	...	...	...
Начальное значение 6	...		...
Начальное значение 7	...		...
Начальное значение 8	...		...
Начальное значение 9	Наилучшее подмножество признаков	...	Наилучшее подмножество признаков

Кроме схемы разделения данных, описанной в материалах настоящей заявки, следующий файл конфигурации использовался для каждого прогона GA. Каждый прогон GA состоит из 3 независимых экспериментов с максимумом в 800000 испытаний для каждого эксперимента.

Для каждого из наилучшего подмножества признаков в вышеприведенной таблице проводилась проверка достоверности, и значения «чувствительности» (рассчитываемой в качестве количества ошибочно классифицированных истинно-положительных результатов) и «специфичности» (рассчитываемой в качестве % уменьшения ложно положительных результатов) получались и усреднялись для всех 10 начальных значений. Некоторое количество диаграмм разброса данных (кривых ROC) вычерчивались для сравнения (фиг.7-14).

Одна диаграмма начерчена для каждого размера подмножества. На диаграмме ось абсцисс представляет чувствительность (количество ошибочно классифицированных истинно-положительных результатов), ось ординат представляет специфичность (% уменьшения ложно положительных результатов). Есть 3 кривых на каждой диаграмме, созданных результатами проверки действительности при 16 коэффициентах (1,5, 1,6, 1,7 ... 3,0) сокращения.

Как показано на диаграммах, за исключением размера 11 и 12, подмножества признаков, выбранные «Систематическим сокращением - коэффициент 2», работают лучше (дают более высокую специфичность), чем подмножества признаков, выбранных «Случайным сокращением», когда допускается ошибочная классификация 1-2 истинных включений (является приемлемым количеством). Это отражено тем обстоятельством, что когда x имеет значение между 1 и 2, кривая Признаков с коэффициентом 2 (Factor2Features) находится выше кривой Случайных признаков (RandomFeatures).

Этот пример показывает, что подмножество признаков, выбранное посредством способа, является лучшим (получена большая специфичность), чем предыдущий основанный на случайном прореживании данных выбор подмножества признаков GA.

Более того, будет очевидно, что другие и дополнительные формы изобретения и варианты осуществления, иные, чем отдельные и примерные варианты осуществления, описанные выше, могут быть придуманы, не выходя из сущности и объема прилагаемой формулы изобретения и ее эквивалентов, а потому предполагается, что объем этого изобретения охватывает эти эквиваленты, и что описание и формула изобретения подразумеваются примерными и не должны интерпретироваться в качестве дополнительно ограничивающих.

1. Способ улучшения точности классификации и уменьшения ложно положительных результатов в извлечении данных, компьютеризованном обнаружении, компьютеризованной диагностике и искусственном интеллекте, способ состоит в том, что:выбирают набор данных обучения из набора обучающих прецедентов с использованием систематического прореживания данных; исоздают классификатор на основании набора данных обучения с использованием способа классификации, при этом способ систематического прореживания данных и способ классификации создают классификатор, тем самым уменьшая ложно положительные результаты и улучшая точность классификации.

2. Способ по п.1, в котором классификатор выбирают из группы, состоящей из: машин опорных векторов, нейронных сетей и деревьев решений.

3. Способ по п.1, способ дополнительно состоит в том, что оценивают классификатор, созданный способом классификации на основании набора данных обучения с использованием набора тестирования.

4. Способ по п.1, в котором выбор дополнительно состоит в том, что удаляют из набора данных обучения ложные включения, которые формируют связи Томска с истинными включениями до тех пор, пока не будет удовлетворено пороговое значение.

5. Способ по п.4, в котором пороговое значение определяют относительно коэффициента сокращения x из условия, чтобы количество ложных включений, оставшихся в наборе данных обучения после систематического прореживания данных, было не большим, чем взятое x раз количество истинных включений в наборе данных обучения.

6. Способ по п.1, в котором способ дополнительно состоит в том, что проверяют достоверность классификатора с помощью набора обучающих прецедентов или его подмножества.

7. Способ по п.1, который выполняется с использованием генетического алгоритма.

8. Способ по п.7, в котором генетический алгоритм является алгоритмом СНС.

9. Способ выбора признаков из пула признаков, способ состоит в том, что: предоставляют каждый из первого генетического алгоритма и второго генетического алгоритма, при этом первый генетический алгоритм используют для определения наилучшего размера набора признаков; и фиксируют размер набора признаков и используют второй генетический алгоритм для выбора признаков.

10. Способ по п.9, в котором, при предоставлении первого генетического алгоритма, способ дополнительно состоит в том, что анализируют результаты с использованием, по меньшей мере, одного из: количества вхождений хромосом, представляющих разные размеры подмножеств признаков и количества средних ошибок.

11. Способ по п.10, в котором количество средних ошибок является количеством ошибочно классифицированных легочных включений.

12. Машиночитаемый носитель, который, когда приводится в исполнение, реализует способ по п.1.

13. Изделие, которое является устройством формирования изображений, при этом устройство включает в себя компьютер, который запрограммирован для анализа данных изображения посредством реализации способа по п.1.

14. Изделие по п.13, при этом устройство формирования изображения выбрано из группы, состоящей из: компьютерной томографии (СТ), компьютерной аксиальной томографии (CAT), многослоевой компьютерной томографии (MSCT), послойного рентгеновского исследования, ультразвука, отображения магнитного резонанса (MRI), магнитно-резонансной томографии (MRT), ядерного магнитного резонанса (NMR), рентгенографии, микроскопии, флуороскопии, томографии и цифрового формирования изображения.

15. Изделие по п.13, при этом изделие является системой CAD легочных включений.