Способ формирования опорного сигнала в системе беспроводной связи

Способ формирования опорного сигнала в системе беспроводной связи

Иллюстрации

Показать все

Реферат

Область техники

[1] Данное изобретение относится к беспроводной связи и, в частности, к способу формирования опорного сигнала в системе беспроводной связи.

Предшествующий уровень техники

[2] В основном, для различных каналов и сигналов в системе беспроводной связи используется последовательность. Последовательность в системе беспроводной связи должна удовлетворять следующим характеристикам:

[3] (1) хорошие корреляционные характеристики для обеспечения высокого качества детектирования;

[4] (2) низкая CM (Cube Metric - кубическая метрика), повышающая эффективность усилителя мощности;

[5] (3) возможность формирования большого числа последовательностей, чтобы передавать большие объемы информации или обеспечивать планирование ячеек;

[6] (4) возможность формирования в ограниченной форме для уменьшения объема памяти для последовательности.

[7] Нисходящий канал синхронизации используется для выполнения временной и частотной синхронизации между базовой станцией и пользовательским оборудованием и для выполнения поиска ячейки. Нисходящий сигнал синхронизации, то есть последовательность, передается по нисходящему каналу синхронизации, и синхронизация осуществляется посредством операции корреляции с принимаемым нисходящим сигналом синхронизации. Физический ID ячейки может быть идентифицирован посредством нисходящего канала синхронизации. Так как уникальный ID ячейки должен быть идентифицирован, поскольку число доступных последовательностей возрастает, это выгодно с точки зрения планирования ячеек.

[8] Восходящий канал синхронизации используется для выполнения временной и частотной синхронизации и для выполнения доступа для сетевой регистрации, запроса планирования или тому подобное. Последовательность передается по восходящему каналу синхронизации, и каждая соответствующая последовательность распознается как единственно возможная. После детектирования последовательности базовая станция может распознать, через какое возможное пользовательское оборудование передавался восходящий канал синхронизации. В дополнение, через детектированную последовательность могут оцениваться слежение времени, остаточное смещение частоты и тому подобное. Поскольку число возможных вариантов возрастает, вероятность коллизий между единицами пользовательского оборудования может быть уменьшена. Поэтому большое число последовательностей предпочтительно с точки зрения планирования ячеек. Восходящий канал синхронизации называется каналом произвольного доступа (random access channel, RACH) или каналом выбора диапазона в зависимости от системы.

[9] Последовательность может использоваться для передачи управляющей информации по управляющему каналу. Это означает, что управляющая информация, такая как АСK (Acknowledgement, сигнал подтверждения) / NACK (Negative-Acknowledgement, сигнал отрицания подтверждения), CQI (Channel Quality Indicator, индикатор качества канала) и т.д., может отображаться на последовательности. Большое число доступных последовательностей благоприятствует передаче различной управляющей информации.

[10] Скремблирующий код используется для обеспечения рандомизации или понижения отношения пиковой и средней мощностей (peak-to-average power ration - PAPR). С точки зрения планирования ячеек большое число последовательностей благоприятствует использованию для скремблирующих кодов.

[11] Когда несколько пользователей мультиплексируются в отдельном канале с помощью мультиплексирования с кодовым разделением (code division multiplexing, CDM), последовательность может использоваться, чтобы гарантировать ортогональность среди пользователей. Емкость мультиплексирования связана с числом доступных последовательностей.

[12] Опорный сигнал используется приемником для оценки фединга канала и/или используется для демодуляции данных. Кроме того, опорный сигнал используется для достижения синхронизации, когда оборудование пользователя переходит в активный режим от слежения времени/частоты или в режим ожидания. Таким образом, опорный сигнал используется различным образом. Опорный сигнал использует последовательность, и большое число последовательностей выгодно с точки зрения планирования ячеек. Опорный сигнал называется также пилот-сигналом.

[13] Есть два типа восходящих опорных сигналов: опорный сигнал демодуляции и зондирующий опорный сигнал. Опорный сигнал демодуляции используется для оценки канала для демодуляции данных, и зондирующий опорный сигнал используется для планирования пользователей. В частности, восходящий опорный сигнал передается оборудованием пользователя с ограниченной емкостью батарей, поэтому характеристики PARP или СМ последовательностей, используемых для восходящего опорного сигнала, являются критическими. Кроме того, для снижения стоимости оборудования пользователя необходимо уменьшение объема памяти, необходимого для формирования последовательностей.

Раскрытие изобретения

Техническая проблема

[14] Проводился поиск способа формирования последовательности, пригодной для восходящего опорного сигнала.

[15] Проводился поиск способа для передачи восходящего опорного сигнала.

Техническое решение

[16] Проводился поиск способа формирования последовательности, пригодной для восходящего опорного сигнала, как изложено в пункте 1 формулы изобретения.

[17] Более точно, изобретение относится к способу формирования опорного сигнала в системе беспроводной связи, способ содержит получение базовой последовательности x_u(n) и получение последовательности r(n) опорного сигнала длины N из базовой последовательности x_u(n), причем базовая последовательность x_u(n) выражается как

[18]

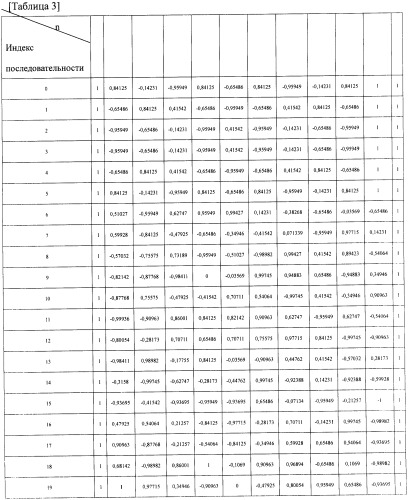
[19] и, если N=12, то, по меньшей мере, одно из значений, предусмотренных в приведенной ниже таблице, используется как значение фазового параметра p(n):

[20]

p(0), …, p(11)
-1 3 -1 1 1 -3 -3 -1 -3 -3 3 -1
-1 3 1 3 1 -1 -1 3 -3 -1 -3 -1
-1 -3 1 1 1 1 3 1 -1 1 -3 -1
-1 3 -3 3 -1 3 3 -3 3 3 -1 -1

[21] Далее, если N=24, то, по меньшей мере, одно из значений, предусмотренных в приведенной ниже таблице, может быть использовано как значение фазового параметра p(n):

[22]

p(0), …, p(23)
-1 -3 3 -1 -1 -1 -1 1 1 -3 3 1 3 3 1 -1 1 - 3 1 - 3 1 1 -3 -1
-1 -3 3 -3 -3 -3 -1 -1 -3 -1 -3 3 1 3 -3 -1 3 -1 1 -1 3 - 3 1
-1 -1 1 -3 1 3 -3 1 -1 -3 -1 3 1 3 1 -1 -3 -3 -1 -1 -3 -3 -3
-1 -3 1 1 3 -3 1 1 -3 -1 -1 1 3 1 3 1 -1 3 1 1 -3 -1 -3 -1
-1 -3 -1 -1 1 -3 -1 -1 1 -1 -3 1 1 -3 1 -3 -3 3 1 1 -1 3 -1

[23] Последовательность r(n) опорного сигнала может быть получена как

[24]

[25] циклическим сдвигом α базовой последовательности x_u(n).

[26] Кроме того, осуществляется поиск способа для передачи восходящего опорного сигнала, как изложено в пункте 4 формулы изобретения.

[27] Более конкретно, изобретение относится к способу для передачи опорного сигнала в системе беспроводной связи, способ содержит получение последовательности r(n) опорного сигнала длины N из базовой последовательности x_u(n), отображение последовательности опорного сигнала на N поднесущих частотах и передачу отображаемой последовательности опорного сигнала на восходящий канал, причем базовая последовательность x_u(n) выражается как

[28] ,

[29] и если N=12, то, по меньшей мере, одно из значений, предусмотренных в приведенной ниже таблице, используется как значение фазового параметра p(n):

[30]

p(0), …, p(11)
-1 3 -1 1 1 -3 -3 -1 -3 -3 3 -1
-1 3 1 3 1 -1 -1 3 -3 -1 -3 -1
-1 -3 1 1 1 1 3 1 -1 1 -3 -1
-1 3 -3 3 -1 3 3 -3 3 3 -1 -1

[31] В еще одном аспекте, способ для передачи опорного сигнала в системе беспроводной связи включает получение последовательности r(n) опорного сигнала, имеющего длину N, из базовой последовательности x_u(n), отображение последовательности опорного сигнала на N поднесущих частотах и передачу отображаемой последовательности опорного сигнала на восходящий канал.

Положительные эффекты

[32] Последовательности, формируемые с помощью формулы формирования в замкнутой форме, сравниваются со сравнительными последовательностями, из которых те, которые имеют хорошие корреляционные и СМ характеристики, используются как восходящий опорный сигнал. Хотя эти последовательности с хорошими корреляционными и СМ характеристиками используются наряду со сравнительными последовательностями как восходящий опорный сигнал, желаемые характеристики последовательностей могут быть поддержаны, чтобы таким образом улучшить характеристики демодуляции данных и выполнить точное планирование в восходящем канале.

Краткое описание чертежей

[33] Фиг.1 представляет собой блок-схему передатчика в соответствии с вариантом осуществления настоящего изобретения.

[34] Фиг.2 представляет собой блок-схему формирователя сигналов в соответствии с SC-FDMA схемой.

[35] Фиг.3 показывает структуру радиокадра.

[36] Фиг.4 представляет собой примерный вид, показывающий сетку ресурсов для восходящего слота.

[37] Фиг.5 показывает структуру восходящего субкадра.

[38] Фиг.6 представляет собой концептуальный вид, показывающий циклическое расширение.

[39] Фиг.7 показывает способ усечения.

[40] Фиг.8 представляет собой блок-схему, иллюстрирующую процесс способа передачи опорного сигнала в соответствии с вариантом осуществления настоящего изобретения.

Принцип работы изобретения

[41] В дальнейшем, нисходящий канал относится к связи от базовой станции (base station, BS) с оборудованием пользователя (user equipment, UE), и восходящий канал относится к связи от UE к BS. В нисходящем направлении, передатчик может быть частью BS и приемник может быть частью UE. В восходящем направлении, передатчик может быть частью UE и приемник может быть частью BS. Оборудование пользователя (UE) может быть фиксированным или подвижным и может называться другой терминологией, такой как подвижная станция (MS), терминал пользователя (user terminal, UT), абонентская станция (subscriber station, SS), беспроводное устройство (wireless device) и т.д. Станция BS обычно является фиксированной станцией, которая связывается с UE и может называться другой терминологией, такой как Node В, базовая приемопередающая система (base transceiver system, BTS), точка доступа (access point) и т.д. Может быть одна или более ячеек в пределах зоны покрытия BS.

[42] I. Система

[43] Фиг.1 представляет собой блок-схему, изображающую передатчик в соответствии с вариантом осуществления настоящего изобретения.

[44] Ссылаясь на Фиг.1, передатчик 100 включает формирователь 110 опорного сигнала, процессор 120 данных, устройство отображения 130 физических ресурсов и формирователь 140 сигналов.

[45] Формирователь 110 опорного сигнала формирует последовательность для опорного сигнала. Имеется два типа опорных сигналов: опорный сигнал демодуляции и зондирующий опорный сигнал. Опорный сигнал демодуляции используется для оценки канала для демодуляции данных, и зондирующий опорный сигнал используется для планирования восходящего канала. Та же последовательность опорного сигнала может быть использована для опорного сигнала демодуляции и зондирующего опорного сигнала.

[46] Процессор 120 данных обрабатывает пользовательские данные для формирования символов с комплексными значениями. Устройство 130 отображения физических ресурсов отображает символы с комплексными значениями для последовательности опорного сигнала и для пользовательских данных на физические ресурсы. Символы с комплексными значениями могут быть отображены на взаимоисключающие физические ресурсы. Физические ресурсы могут быть названы ресурсными элементами или поднесущими частотами.

[47] Формирователь 140 сигналов формирует сигнал временной области для передачи через передающую антенну 190. Формирователь 140 сигналов может формировать сигнал временной области в соответствии со схемой множественного доступа с частотным разделением с одной несущей частоты (single carrier-frequency division multiple access, SC-FDMA) и, в этом случае, сигнал временной области на выходе формирователя 140 сигналов называется SC-FDMA символом или символом множественного доступа с ортогональным частотным разделением (orthogonal frequency division multiple access, OFDMA).

[48] В нижеследующем описании предполагается, что формирователь 140 сигналов использует схему SC-FDMA, но это лишь в качестве примера и нет ограничения на схему множественного доступа, к которой применяется настоящее изобретение. Например, настоящее изобретение может быть применено для различных других схем множественного доступа, таких как OFDMA, множественный доступ с кодовым разделением каналов (code division multiple access, CDMA), множественный доступ с временным разделением каналов (time division multiple access, TDMA) или множественный доступ с частотным разделением каналов (frequency division multiple access, FDMA).

[49] Фиг.2 представляет собой блок-схему формирователя сигналов в соответствии с SC-FDMA схемой.

[50] Со ссылкой на Фиг.2, формирователь 200 сигналов включает блок 220 дискретного преобразования Фурье (discrete Fourier transform, DFT) для выполнения дискретного преобразования Фурье (DFT), устройство отображения 230 поднесущих частот и блок 240 обратного быстрого преобразования Фурье (inverse fast Fourier transform, IFFT) для выполнения обратного быстрого преобразования Фурье (IFFT). Блок 220 DFT выполняет DFT над входными данными и на выходе образует символы в частотной области. Устройство отображения 230 поднесущих частот отображает символы в частотной области на каждую поднесущую частоту, и блок 230 IFFT выполняет IFFT над входными символами, чтобы на выходе получить сигнал во временной области.

[51] Опорный сигнал может формироваться во временной области и поступать на вход блока 220 DFT. Альтернативно, опорный сигнал может формироваться в частотной области и напрямую отображаться на поднесущие частоты.

[52] Фиг.3 показывает структуру радиокадра.

[53] Со ссылкой на Фиг.3, радиокадр включает десять субкадров. Каждый субкадр включает два слота. Интервал для передачи отдельного субкадра называется интервалом передачи (transmission time interval, TTI). Например, TTI может быть 1 миллисекунда (мс) и интервал отдельного слота может быть 0,5 мс. Слот может включать множество SC-FDMA символов во временной области и множество блоков ресурсов в частотной области.

[54] Структура радиокадра является просто примером, и число субкадров, включаемых в радиокадр, число слотов, включаемых в субкадр, и число SC-FDMA символов, включаемых в слот, может меняться.

[55] Фиг.4 показывает сетку ресурсов для восходящего слота.

[56] Ссылаясь на Фиг.4, восходящий слот включает множество SC-FDMA символов во временной области и множество блоков ресурсов в частотной области. Здесь, показывается, что восходящий слот включает семь SC-FDMA символов, и блок ресурсов включает двенадцать поднесущих частот, но это просто примеры, и настоящее изобретение не ограничивается этим.

[57] Каждый элемент сетки ресурсов называется элементом ресурсов. Отдельный блок ресурсов включает 12×7 элементов ресурсов. Число (N^UL) блоков ресурсов, включаемых в восходящий слот, зависит от пропускной способности передачи в восходящем канале.

[58] Фиг.5 показывает структуру восходящего субкадра.

[59] Со ссылкой на Фиг.5, восходящий субкадр может быть разделен на две части: область управления и область данных. Средняя часть субкадра распределяется для области данных, и обе боковые части области данных распределяются для области управления. Область управления - это область для передачи сигналов управления, которые обычно распределяются для канала управления. Область данных - это область для передачи данных, которые обычно распределяются для канала данных. Канал, распределяемый для области управления, называется физическим восходящим каналом управления (physical uplink control channel, PUCCH), и канал, распределяемый для области данных, называется физическим восходящим общим каналом (physical uplink shared channel, PUSCH). Оборудование UE не может одновременно передавать PUCCH и PUSCH.

[60] Сигнал управления включает сигнал АСK (Acknowledgement - подтверждение) / NACK (Negative-Acknowledgement - отрицание подтверждения), который является обратной связью (feedback) гибридного автоматического запроса повторения (hybrid automatic repeat request, HARQ) для нисходящего потока данных, индикатор качества канала (channel quality indicator, CQI), указывающий состояние нисходящего канала, сигнал запроса планирования (scheduling request signal), который используют для запроса восходящих радиоресурсов, и т.п.

[61] Канал PUCCH использует отдельный блок ресурсов, который занимает взаимно различные частоты в каждом из двух слотов субкадра. Два блока ресурсов, распределяемых для PUCCH, перескакивают по частоте на границе слота. Здесь, иллюстрируется, что два канала PUCCH, один, имеющий m=0, и другой, имеющий m=1, распределяются для субкадра, но множество каналов PUCCH может быть распределено для субкадра.

[62] II. Последовательность Zadoff-Chu (ZC)

[63] Последовательность Zadoff-Chu (ZC) обычно используется в беспроводной связи из-за хороших СМ характеристик и корреляционных характеристик. Последовательность ZC является одной из последовательностей на основе последовательностей с постоянной амплитудой и нулевой автокорреляцией (constant amplitude and zero auto correlation, CAZAC). ZC последовательность имеет идеальные характеристики с постоянной амплитудой как в частотной области, так и во временной области через DFT (или IDFT) и периодическую автокорреляцию в форме импульса. Таким образом, применение ZC последовательности к OFDMA или SC-FDMA на основе DFT показывает очень хорошие PAPR (или СМ) характеристики.

[64] Формула формирования ZC последовательности с длиной N_zc имеет следующий вид:

[65] Математическое выражение 1

[Формула 1]

[66] где 0≤m≤N_ZC-1, и 'u' обозначает индекс корня, который является реальным числом не больше, чем N_ZC. Индекс u корня представляет собой относительно простое число с N_ZC. Это означает, что когда N_ZC определено, число индексов становится числом доступных корневых ZC последовательностей. Соответственно, когда Nzc является простым числом, наибольшее число корневых ZC последовательностей может быть обеспечено. Например, если N_ZC равна 12, которое является составным числом, число доступных корневых ZC последовательностей равно 4 (u=1, 5, 7, 11). Если N_ZC является 13, которое является простым числом, число доступных корневых ZC последовательностей равно 12 (u=1, 2, …, 10).

[67] В общем, ZC последовательность, имеющая длину простого числа, имеет лучшие СМ или корреляционные характеристики, чем ZC последовательности, имеющие длину составного числа. Исходя из этого, существует два способа для увеличения числа ZC последовательностей, когда длина ZC последовательности, требуемой для формирования, не является простым числом. Один из способов основан на циклическом расширении, и другой способ основан на усечении.

[68] Фиг.6 представляет собой концептуальный вид, показывающий способ циклического расширения. Способ циклического расширения относится к способу, в котором (1) когда длина требуемых ZC последовательностей равна 'N', (2) ZC последовательности формируются путем выбора простого числа меньше, чем требуемая длина N как N_ZC, и (3) формируемые ZC последовательности циклически расширяются на оставшуюся часть (N-N_ZC), чтобы сформировать ZC последовательности с длиной N. Например, если N равно 12, то N_ZC выбирается 11, чтобы получить все 10 циклически расширенных ZC последовательностей.

[69] Путем использования ZC последовательности x_u(m) формулы 1 циклически расширенные последовательности r_CE(n) могут быть выражены, как показано ниже.

[70] Математическое выражение 2

[Формула 2]

[71] где 0≤n≤N-1, «а mod b» обозначает операцию по модулю, которая означает остаток, обеспечиваемый делением 'а' на 'b1', и N_ZC обозначает наибольшее простое число среди натуральных чисел не больше, чем N.

[72] Фиг.7 представляет собой концептуальный вид, показывающий способ усечения. Способ усечения относится к способу, в котором (1) когда длина требуемых ZC последовательностей равна N, (2) выбирается N_ZC как простое число большее, чем требуемая длина N, чтобы сформировать ZC последовательности, и (3) оставшаяся часть (Nzc-N) усекается, чтобы формировать ZC последовательности с длиной N. Например, если N равно 12, Nzc выбирается равным 13, чтобы обеспечить все двенадцать усеченных ZC последовательностей.

[73] Путем использования ZC последовательности x_u(m) формулы 1 усеченные и формируемые последовательности r_TR(n) могут быть выражены, как показано ниже.

[74] Математическое выражение 3

[Формула 3]

[75] где 0≤n≤N-1, и Nzc обозначает наименьшее простое число среди натуральных чисел не меньше, чем N.

[76] Когда последовательности формируются путем использования описанных выше ZC последовательностей, число доступных последовательностей максимизируется, когда Nzc является простым числом. Например, если длина N требуемой последовательности равна 11, когда ZC последовательности Nzc=11 формируются, то число доступных последовательностей максимально равно 10. Если количество требуемой информации или число используемых последовательностей должно быть более чем десять последовательностей, то ZC последовательность не может использоваться.

[77] Если длина требуемой последовательности равна N=12, то выбирается N_ZC=11 и циклическое расширение выполняется или Nzc=13 выбирается и усечение выполняется, чтобы таким образом формировать десять ZC последовательностей в случае циклического расширения и двенадцать ZC последовательностей в случае усечения. В этом случае, однако, если больше последовательностей требуется (например, 30 последовательностей), ZC последовательности, имеющие такие хорошие характеристики, как удовлетворяющие упоминаемым последовательностям, не могут быть сформированы.

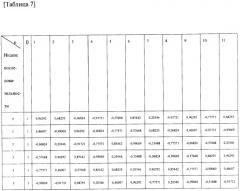
[78] В частности, если требуются последовательности, имеющие хорошие СМ характеристики, то число доступных последовательностей может быть серьезно сокращено. Например, предпочтительно, последовательности, используемые для опорного сигнала, ниже, чем СМ значение в передаче квадратурной фазовой модуляции (quadrature phase shift keying, QPSK), когда рассматривается повышение мощности. Когда используется SC-FDMA схема, СМ значение при QPSK передаче равно 1.2 дБ. Если последовательности, удовлетворяющие QPSK СМ требованиям, выбираются среди доступных ZC последовательностей, то число доступных последовательностей для использования для опорного сигнала будет сокращено. Более подробно, приведенная ниже таблица показывает СМ значения последовательностей, формируемых после циклического расширения путем выбора Nzc=1 в случае, где длина требуемой последовательности равна N=12.

[79] Таблица 1

[Таблица 1]
Индекс	u	СМ [дБ]
последовательности
0	1	0,17
1	2	1,32
2	3	1,50
3	4	0,85
4	5	0,43
5	6	0,43
6	7	0,85
7	8	1,50
8	9	1,32
9	10	0,17

[80] Как указано в таблице выше, если пороговое значение равно 1,2 дБ, требования QPSK СМ, то число доступных последовательностей сокращается с десяти до шести (u=0, 4, 5, 6, 7, 10).

[81] Поэтому требуется способ формирования последовательностей, которые могут иметь хорошие СМ и корреляционные характеристики и могут уменьшить емкость памяти, требуемую для формирования или хранения доступных последовательностей.

[82] III. Формула формирования последовательностей

[83] Формула формирования в замкнутой форме для формирования последовательностей, имеющих хорошие СМ и корреляционные характеристики, является полиномиальным выражением с одинаковым размером и фазовой компонентой k-го порядка.

[84] Формула формирования в замкнутой форме по отношению к последовательности r(n), имеет следующий вид:

[85] Математическое выражение 4

[Формула 4]

, ,

[86] где m=0, 1, …, N-1, N обозначает длину последовательности r(n), и u₀, u₁, …, u_k обозначают произвольные реальные числа. Последовательность x_u(m) является базовой последовательностью для формирования последовательности r(n). Значение 'u' представляет индекс последовательности и находится в один к одному связи с сочетанием u₀, u₁, …, u_k.

[87] Здесь, u_k является компонентой для сдвига фазы всей последовательности и не влияет на формирование последовательности. Таким образом, Формула 4 может быть представлена в следущем виде:

[88] Математическое выражение 5

[Формула 5]

, ,

[89] В отличном примере, формула формирования в замкнутой форме по отношению к последовательности r(n), получаемая путем аппроксимации или квантования фазового значения в последовательности формулы 4, может быть выражена следующим образом:

[90] Математическое выражение 6

[Формула 6]

, ,

[91] где m=0, 1, …, N-1, N обозначает длину последовательности r(n), и u₀, u_1, …, u_k обозначают произвольные реальные числа. Функция quan(.) обозначает функцию квантования, которая означает аппроксимацию или квантованиие до конкретного значения.

[92] Действительное значение и мнимое значение результатов последовательности в Формуле 6 может быть аппроксимировано/квантовано как показано ниже.

[93] Математическое выражение 7

[Формула 7]

, ,

[94] где m=0, 1, …, N-1, и p_n обозначает нормализационный коэффициент для регулирования амплитуды формируемой последовательности.

[95] В Формуле 6, значения на комплексной единичной окружности, которые могут квантоваться в число Nq. Квантованые значения могут аппроксимироваться до координат QPSK {0,7071+j0,7071, 0,7071-j0,7071, -0,7071+j0,7071, -0,7071-j0.7071} или аппроксимироваться до {exp(-j*2*π*0/8), exp(-j*2*π*l/8), exp(-j*2*π*2/8), exp(-j*2*π*3/8), exp(-j*2*π*4/8), exp(-j*2*π*5/8), exp(-j*2*π*6/8), exp(-j*2*π*7/8)} в форме 8-PSK.

[96] В этом случае, в соответствии со способами аппроксимации, упомянутые значения могут быть аппроксимированы до ближайших значений, до тех же или ближайших малых значений или до тех же или ближайших больших значений.

[97] В Формуле 7, реальное значение и мнимое значения, формируемые из значений экспоненциальной функции, аппроксимируются до ближайшего уникального сочетания. То есть, например, они аппроксимируются до M-PSK или M-QAM. Кроме того, реальное значение и мнимое значение могут быть аппроксимированы до {+1, -1, 0} через функцию знака (sign), которая выдает знак значения.

[98] В Формулах 6 и 7, для того чтобы аппроксимировать до ближайшего QPSK, значение u_k может быть установлено на π*1/4. Кроме того, функция округления, означающая округление как конкретная форма функции квантования, может использоваться. Функция квантования может использоваться над фазовой частью функции квантования или над всей экспоненциальной функцией.

[99] Переменные могут быть установлены в соответствии с конкретным критерием, чтобы формировать последовательности из формул формирования. Критерий может рассматривать СМ или корреляционные характеристики. Например, СМ значение и порог взаимной корреляции могут быть установлены, чтобы формировать последовательности.

[100] Подробные формулы формирования для формирования последовательностей из описанных выше общих формул формирования будут теперь описаны.

[101]

[102] Первый вариант осуществления: простая форма полиномиального выражения (k=3)

[103] Следующая формула формирования может быть выбрана:

[104] Математическое выражение 8

[Формула 8]

, ,

[105] где m=0, 1, …, N-1, N обозначает длину последовательности r(n), и u₀, u_1, u₂ обозначают произвольные реальные числа.

[106]

[107] Второй вариант осуществления: модифицированная ZC последовательность

[108] Следующая формула формирования может быть выбрана:

[109] Математическое выражение 9

[Формула 9]

, ,

[110] где m=0,1, …, N-1, N обозначает длину последовательности r(n), и u₀, u₁, …, u_k-1 обозначают произвольные реальные числа.

[111] Эта формула формирования имеет следующие преимущества. Во-первых, ZC последовательности, имеющие хорошие характеристики, которые могут быть созданы с длиной N, могут включаться в набор доступных последовательностей. Например, если k=2, u₁=0 и u₀ является целым числом, она эквивалентна ZC последовательности, когда N в Формуле 1 является четным числом. Если k=2, u₁ и u₀ являются целыми числами, и u₁=u₀, она эквивалентна ZC последовательности, когда N в Формуле 1 является нечетным числом. Во-вторых, последовательности, имеющие хорошие характеристики, так близки, как Евклидово расстояние исходной оптимизированной ZC последовательности.

[112]

[113] Третий вариант осуществления: циклически расширенная скорректированная ZC последовательность

[114] Следующая формула формирования может быть выбрана:

[115] Математическое выражение 10

[Формула 10]

, ,

[116] где m=0, 1, …, N-1, N обозначает длину последовательности r(n), и u₀, u₁, …, u_k-1 обозначают произвольные реальные числа. Число N_ZC является наибольшим простым числом среди натуральных чисел меньше, чем N. Эта формула формирования выгодна тем, что существующая ZC последовательность может включаться в набор доступных последовательностей. Например, если k=2, u₁ и u₀ являются целыми числами, и u₁=u₀, она эквивалентна значению, получаемому циклическим расширением ZC последовательности.

[117]

[118] Четвертый вариант осуществления: усеченная модифицированная ZC последовательность

[119] Следующая формула формирования может быть выбрана:

[120] Математическое выражение 11

[Формула 11]

, ,

[121] где m=0, 1, …, N-1, N обозначает длину последовательности r(n), и u₀, u₁, …, u_k-1 обозначают произвольные реальные числа. Число N_ZC является наибольшим простым числом среди натуральных чисел больше, чем N. Эта формула формирования выгодна тем, что существующая ZC последовательность может включаться в набор доступных последовательностей. Например, если k-2, и u₁ и u₀ являются целыми числами, то она эквивалентна значению, получаемому усечением ZC последовательности.

[122]

[123] Пятый вариант осуществления: модифицированная ZC последовательность, имеющая ограничение.

[124] Следующая формула формирования может быть выбрана:

[125] Математическое выражение 12

[Формула 12]

, ,

[126] где m=0, 1, …, N-1, N обозначает длину последовательности r(n), u₀, u₁, …, u_k-1 обозначают произвольные числа, и 'а' обозначает произвольное реальное число, 'а' служит, чтобы ограничить дробность переменных u₀, u₁, …, u_k-1. Потому что дробность переменных u₀, u₁, …, u_k-1 может быть преобразована в целую единицу через такое ограничение, объем памяти, требуемой для хранения информации последовательности, может быть уменьшен.

[127]

[128] Шестой вариант осуществления: модифицированная ZC последовательность, имеющая два ограничения

[ 129] Следующая формула формирования может быть выбрана:

[130] Математическое выражение 13

[Формула 13]

, ,

[131] где m=0, 1, …, N-1, N обозначает длину последовательности r(n), u₀, u₁, …, u_k-1 обозначают произвольные числа, 'а' обозначает произвольное реальное число, и b₀, b₁, …, b_k-1 обозначают произвольные реальные числа, 'а' служит, чтобы ограничить дробность переменных u₀, u₁, …, u_k-1. Возможно различное ограничение переменных через b₀, b₁, …, b_k-1. Объем памяти, требуемый для хранения информации последовательности, может быть уменьшен путем изменения дробности переменных u₀, u₁, …, u_k-1 на единицу целого числа через два ограничения, и последовательность с лучшими характеристиками может быть обеспечена путем регулирования дробности переменных.

[132]

[133] Седьмой вариант осуществления: модифицированная ZC последовательность (k=3), имеющая два ограничения

[134] Следующая формула формирования может быть выбрана:

[135] Математическое выражение 14

[Формула 14]

, ,

[136] где m=0, 1, …, N-1, N обозначает длину последовательности r(n), u₀, u₁, u₂ обозначают произвольные числа, 'а' обозначает произвольное реальное число, и b₀, b₁, b₂ обозначают произвольные числа, 'а' служит, чтобы ограничить дробность переменных u₀, u_1, u₂. Возможно различное ограничение переменных через b₀, b₁, b₂.

[137]

[138] Восьмой вариант осуществления: модифицированная ZC последовательность, имеющая одно ограничение и циклическое расширение

[139] Следующая формула формирования может быть выбрана:

[140] Математическое выражение 15

[Формула 15]

, ,

[141] где m=0, 1, …, N_zc-1, N обозначает длину последовательности r(n), u₀,u₁, …, u_k-1 обозначают произвольные числа, 'а' обозначает произвольное реальное число, и N_ZC обозначает наибольшее простое число среди натуральных чисел меньше, чем 'N'. Число 'а' служит, чтобы ограничить дробность переменных u₀, u₁, …, u_k-1. Из-за дробности переменных u₀, u₁, …, u_k-1 могут быть изменены на единицу целого через такое ограничение, объем памяти, требуемый для хранения информации последовательности, может быть уменьшен.

[142]

[143] Девятый вариант осуществления: модифицированная ZC последовательность, имеющая два ограничения и циклическое расширение

[144] Следующая формула формирования может быть выбрана:

[145] Математическое выражение 16

[Формула 16]

, ,

[146] где m=0, 1, N_ZC-1, N обозначает длину последовательности r(n), u₀, u₁, …, u_k-1 обозначают произвольные числа, 'a' обозначает произвольное реальное число, b₀, b₁, …, b_k-1 обозначают произвольные числа, и N_ZC обозначает наибольшее простое число среди натуральных чисел меньше, чем 'N'. Число 'a' служит, чтобы ограничить дробность переменных u₀, u₁, …, u_k-1. Возможно различное ограничение переменных через b₀, b₁, …, b_k-1. Объем памяти, требуемой для хранения информации последовательности, может быть уменьшена путем