Способ использования трех gps-частот для решения неопределенности фазы несущей

Способ использования трех gps-частот для решения неопределенности фазы несущей

Иллюстрации

Показать все

Реферат

Настоящее изобретение в целом относится к приемникам и способам определения положения объекта в системах позиционирования, таких как система глобального позиционирования (GPS) или европейская система Galileo, и, в частности, к способам разрешения неопределенности числа фазовых циклов несущей при измерениях по фазе несущей в системах позиционирования, использующих три частоты.

УРОВЕНЬ ТЕХНИКИ

Глобальная система позиционирования, такая как GPS, использует группу спутников для позиционирования или ведения объектов на земле. В настоящее время группа спутников передает сигналы на двух несущих частотах: частоте L1 на (154*10,23 МГц) или 1575,42 МГц и частоте L2 на (120*10,23 МГц) или 1227,6 МГц, которые соответствуют длине волны L1, равной 0,1903 м, и длине волны L2, равной 0,2442 соответственно. Для каждой несущей частоты GPS-приемник, как правило, выполняет два типа измерений для определения положения объекта. Эти два типа измерений - измерение псевдодальности и интегрированное измерение по фазе несущей. Измерение псевдодальности (или кодовое измерение) - это базисная возможность, которой обладают GPS-приемники всех типов. При этом используются C/A или P коды, модулированные в сигналах несущей. Измерение по фазе несущей выполняется интегрированием восстановленной несущей сигнала при его поступлении в приемник. Из-за того что с момента начала отслеживания приемником фазы несущей полное число циклов между спутником и приемником неизвестно, возникает неопределенность числа циклов. Эта неопределенность числа циклов должна быть решена для того, чтобы добиться высокой точности при измерениях по фазе несущей.

Имея результаты измерений, можно вычислить дальность или расстояние между GPS-приемником и каждым из множества спутников, умножив время прохождения сигнала на скорость света. Эти дальности обычно называют псевдодальностями (ошибочными дальностями), поскольку измерения могут включать в себя ошибки, возникающие из-за различных факторов, таких как ошибка относительно часов спутника, ошибка эфемерид, эффекты ионосферной и тропосферной рефракции, собственный шум приемника, помех типа "повторное изображение" и т.д. Для того чтобы исключить или уменьшить эти ошибки, в GPS-приложениях, как правило, используются дифференциальные операции. Дифференциальная GPS (DGPS), как правило, включает в себя базовый GPS-приемник, пользовательский GPS-приемник и механизм связи между базовым и пользовательским приемниками. Базовый приемник размещается в пункте с известными координатами, и известное положение используется для расчета поправок для некоторых или всех перечисленных выше факторов ошибок. Рассчитанные поправки или необработанные данные с базовой станции передаются пользовательскому приемнику, который затем использует их для соответствующей поправки рассчитанного положения. Дифференциальные операции, использующие измерения по фазе несущей частоты, часто называются позиционированием методом кинематической съемки в реальном времени (RTK).

Однако рассчитанные поправки или необработанные данные с базовой станции полезны для пользовательского GPS-приемника только тогда, когда имеется пространственная и временная корреляция ошибок у базового и пользовательского приемников. В то время как ошибки относительно часов спутника, влияющие на измерение псевдодальности или по фазе несущей частоты, превосходно коррелируют между базовым и пользовательским приемником, большинство других факторов ошибок либо не коррелируют, либо корреляция уменьшается при использовании на широких площадях, т.е. тогда, когда расстояние между базовым и пользовательским приемником становится большим. Более того, когда расстояние между пользовательским и базовым приемником становится большим, более 10-20 километров, двух несущих частот в существующей GPS-системе становится недостаточно для решения неопределенности числа фазовых циклов несущей.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Настоящее изобретение включает в себя способ для генерации скорректированных измерений по фазе несущей с вычисленной неопределенностью и минимальным шумом. В одном из вариантов осуществления первое скорректированное композитное измерение по фазе несущей с вычисленной неопределенностью формируется с помощью трех измерений по фазе несущей на трех несущих частотах. Второе скорректированное композитное измерение по фазе несущей с минимальным шумом формируется с использованием первичных измерений по фазе несущей. Наконец, первое композитное измерение по фазе несущей сглаживается с помощью второго композитного измерения по фазе несущей.

В некоторых вариантах осуществления второе композитное измерение по фазе несущей включает в себя нерешенную неопределенность числа полных циклов. Неопределенность числа полных циклов решается оценкой скорректированной на рефракцию длины волны для второго композитного измерения. Сглаженная величина коррекции определяется взятием разности между первым и вторым композитными измерениями. Далее сглаженная величина коррекции делится на длину волны, скорректированную на рефракцию. Затем результат округляется до ближайшего целого как неопределенность фазы. Скорректированное композитное измерение по фазе несущей с вычисленной неопределенностью и минимальной фазой получается суммированием второго композитного измерения и результата умножения длины волны, скорректированной на рефракцию, и неопределенности фазы.

Возможность решить неопределенности в скорректированных композитных измерениях в большой степени удалит ограничения в использовании дифференциальных GPS по фазе несущей, и, таким образом, глобальная RTK-возможность станет практически осуществимой.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

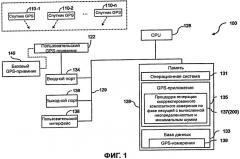
Фиг.1 - это блок-схема компьютерной системы, которая может быть использована для реализации способа генерации скорректированного измерения по фазе несущей с вычисленной неопределенностью и минимальным шумом.

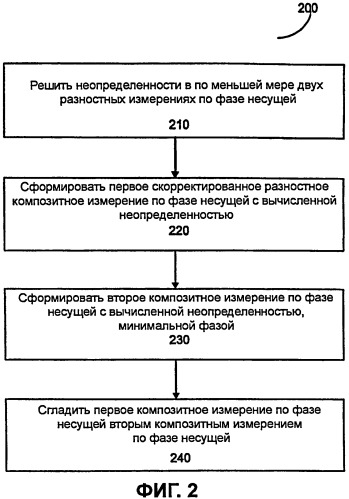
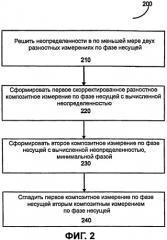
Фиг.2 - это блок-схема, иллюстрирующая способ для генерации скорректированных измерений по фазе несущей с вычисленной неопределенностью и минимальным шумом.

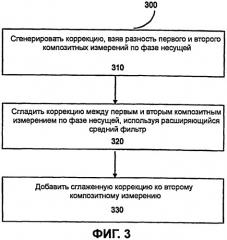
Фиг.3 - это блок-схема, иллюстрирующая процесс сглаживания, используемый в способе генерации скорректированного измерения по фазе несущей с вычисленной неопределенностью и минимальным шумом.

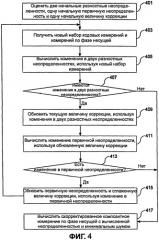
Фиг.4 - это блок-схема, иллюстрирующая дополнительный процесс сглаживания, используемый в способе генерации скорректированного измерения по фазе несущей с вычисленной неопределенностью и минимальным шумом.

ПОДРОБНОЕ ОПИСАНИЕ

Фиг.1 иллюстрирует компьютерную систему 100, которая может использоваться для выполнения способа для генерации скорректированного композитного измерения по фазе несущей с вычисленной неопределенностью и минимальным шумом в соответствии с одной из реализаций настоящего изобретения.

Компьютерная система 100 соединена с пользовательским GPS-приемником 122, который передает в компьютерную систему 100 GPS кодовые измерения и измерения по фазе несущей, основанные на сигналах от множества спутников 110-1, 110-2, …, 110-n, где n - число спутников, видимых пользовательским GPS-приемником 122. Пользовательский GPS-приемник 100 может обмениваться данными с базовым GPS-приемником 140, также выполняющим измерения, основанные на сигналах от множества спутников, используемых для генерации поправок измерений, выполненных пользовательским GPS-приемником. Множество спутников или любой и более из них будут иногда называться в данном документе как спутник(и) 110. В некоторых вариантах осуществления пользовательский GPS-приемник 122 и компьютерная система 100 интегрированы в одно устройство в едином корпусе, такое как ноутбук, карманный компьютер, или даже переносное устройство отслеживания местоположения, устанавливаемые на велосипед, или другая мобильная система позиционирования и/или навигации. В других вариантах осуществления пользовательский GPS-приемник 122 и компьютерная система 100 не интегрированы в одно устройство.

Как показано на Фиг.1, компьютерная система 100 включает в себя центральный процессор (CPU) 126, память 128, порт 134 ввода и порт 136 вывода и (опционально) пользовательский интерфейс 138, соединенные друг с другом одной или более коммуникационными шинами 129. Память 128 может включать в себя быстродействующее оперативное запоминающее устройство и может включать в себя энергонезависимую память, такую как один или более магнитных дисковых запоминающих устройств. Память 128 предпочтительно хранит операционную систему 131, базу 133 данных и процедуры 135 GPS-приложения. Процедуры GPS-приложения могут включать в себя процедуры 137, реализующие способ для генерации скорректированного композитного измерения по фазе несущей с вычисленной неопределенностью и минимальным шумом, в соответствии с одной из реализаций настоящего изобретения, как более детально описано ниже. Операционная система 131 и прикладные программы и процедуры 135 и 137, хранящиеся в памяти 128, выполняются CPU 126 компьютерной системы 124. Память 128 предпочтительно хранит структуры данных, используемые во время выполнения процедур 135 и 137 GPS-приложения, включая измерения 139 GPS псевдодальности и/или измерения по фазе несущей, а также и другие структуры данных, обсуждаемые в данном документе.

Порт 134 ввода предназначен для приема данных от GPS-приемника 122, а порт 136 вывода используется для экспорта данных и/или результатов вычислений. Данные и результаты вычислений могут также показываться на дисплее пользовательского интерфейса 138.

Для вычисления неопределенности фазы несущей были разработаны две основные методики. Первую методику часто называют «безгеометрической» ("geometry-free") или методикой «пространства измерений», она использует сглаженные кодовые измерения для определения неопределенности фазы при измерении по фазе несущей. Вторую методику часто называют «геометрической» или «пространства позиций», она использует процесс поиска, позволяющий определить, какая комбинация неопределенностей фазы по отношению к множеству спутников в зоне видимости GPS-приемника дает «наилучшее» решение по некоторому критерию, например, такому, как минимум суммы квадратов остатков измерений.

Имеется несколько преимуществ в использовании безгеометрического подхода для решения неопределенности фазы несущей. Первое преимущество использования безгеометрического подхода заключается в том, что он менее подвержен ошибкам измерений, вызванным эффектами тропосферной рефракции, потому что тропосфера одинаково влияет на кодовые измерения и на измерения по фазе несущей. Второе преимущество безгеометрического подхода заключается в том, что решение неопределенности выполняется на основе «спутник за спутником» в отличие от геометрического подхода, требующего для обеспечения корректного решения наличия в зоне видимости GPS-приемника по меньшей мере пяти спутников. Третье преимущество безгеометрического подхода заключается в том, что движение пользовательского GPS-приемника не влияет на разность между кодовыми измерениями и измерениями по фазе несущей, в то время как геометрический подход может требовать транслировать положение пользовательского GPS-приемника заранее вперед, во время движения пользователя. Также, поскольку безгеометрический подход использует большую степень свободы, чем геометрический, в случае безгеометрического подхода проще проверить, что было найдено верное решение неопределенности фазы. Эти преимущества делают безгеометрический подход более предпочтительным для RTK-приложений.

С двумя несущими частотами L1 и L2 безгеометрическая методика используется для решения неопределенности фазы последовательным способом, в котором неопределенности решаются сначала для комбинаций измерений, имеющих самую большую длину волны. Наиболее часто используемая разностная комбинация - это простая разность между измерениями по фазе несущей на двух имеющихся частотах L1 и L2, далее обозначаемая как разность измерений (L1-L2). Разность измерений (L1-L2) имеет приблизительную длину волны в 86,2 см и хорошо подходит для решения неопределенности фазы. Неопределенность фазы в разности измерений (L1-L2) может быть решена с использованием средневзвешенных по частоте кодовых измерений на двух частотах, соответствующих ионосферному искажению в разности измерений по фазе. Затем решенная неопределенность фазы на широкой площади используется для последовательного перехода к меньшим (на меньшей площади) длинам волны. Однако этот подход работает только тогда, когда расстояние между базовым и пользовательским приемниками (базовое расстояние) не превышает некоторого предела, такого как 10-20 километров.

Источник проблемы находится в рассеивающем эффекте ионосферы, воздействующем на две несущие частоты, когда базовое расстояние становится большим. Эффекты ионосферной рефракции негативно влияют на разность измерений (L1-L2). Величина воздействия ионосферной рефракции на разность измерений примерно равна среднему от величины воздействия на каждое из измерений L1 и L2 в отдельности, но противоположного знака. Хотя неопределенность фазы в разности измерений (L1-L2) и может быть решена на больших расстояниях, для того чтобы устранить эффект ионосферной рефракции в разности измерений, также должна быть решена неопределенность фазы в некоторой другой комбинации измерения с другой зависимостью от ионосферы. Комбинация измерения или композитное измерение - это комбинация измерений по фазе на различных несущих частотах.

Имея только две несущие частоты, очень трудно решить неопределенность фазы в любой другой комбинации измерений по фазе несущей, когда базовое расстояние велико. Без наличия третьей частоты, лучшей комбинацией, имеющей очень маленькое искажение, вызванное ионосферной рефракцией, является композитное измерение, образованное с использованием разности между девятикратным измерением по фазе несущей L1 и семикратным измерением по фазе несущей L2, называемое композитным измерением (9L1-7L2). Однако это композитное измерение имеет два очень вредных свойства. Во-первых, эффективная длина волны этого композитного измерения составляет лишь 5,35 сантиметров. Знание величины неопределенности для комбинации измерений (L1-L2) (является ли она четной или нечетной) может быть использовано для увеличения эффективной длины волны с 5,35 до 10,7 сантиметров. Однако по-прежнему невозможно решить скорректированную на рефракцию неопределенность на дальних расстояниях из-за неблагоприятного возрастания многолучевого шума в процессе коррекции рефракции.

Как часть модернизации GPS, гражданским пользователям будет доступен новый сигнал с третьей частотой. Этот новый сигнал по историческим причинам иногда обозначается как сигнал L5 и имеет частоту (115*10,23 МГц) или 1176,45 МГц, и соответствующую длину волны в 0,2548 м. Предложенное добавление третьей частоты к сигналам GPS дает дополнительную степень в конструировании композитных измерений с различными длинами волн, различной чувствительностью к ионосфере и различными эффектами усиления шума и таким образом может помочь в получении скорректированных измерений с решенной неопределенностью фазы, что является критично важным для высокоточных GPS-приложений.

Для последующего использования ниже представлен набор уравнений (1)-(6), определяющих базовые соотношения между кодовыми измерениями и измерениями по фазе несущей на трех частотах, геометрическим расстоянием и ошибкой ионосферной рефракции.

Предположим, что частоты сигналов L1, L2 и L5 называются f_a, f_b и f_c соответственно. Кодовые измерения P_a, P_b, и P_c, ассоциированные с L1, L2 и L5, определяются уравнениями

где ρ - это геометрическое расстояние (включая ошибку тропосферной рефракции) и I - ошибка ионосферной рефракции.

Соответствующие масштабированные измерения по фазе Φ_a, Φ_b и Φ_c на трех частотах определяются уравнениями

где φ_a, φ_b и φ_c обозначают соответствующие сырые измерения по фазе несущей на трех частотах N_a, N_b и N_c, а с - это скорость света.

Фиг.2 иллюстрирует способ 200 для генерации скорректированного композитного измерения по фазе несущей с вычисленной неопределенностью и минимальным шумом в соответствии с одной из реализаций настоящего изобретения. Как показано на Фиг.2, способ 200 включает в себя операцию 210, в которой неопределенности решаются, по меньшей мере, в двух разностных измерениях, каждое из которых формируется, используя разность между масштабированными измерениями по фазе несущей, взятыми на двух из трех частот.

Например, для того, чтобы решить разностную неопределенность в разности измерений по фазе (L1-L2), берется средневзвешенное по частоте от уравнений (1) и (2) определяющее соотношение между композитным кодовым измерением и ошибкой ионосферной рефракции как

Вычитая уравнение (5) из уравнения (4), получаем аналогичное соотношение между двумя измерениями по фазе несущей и ошибкой ионосферной рефракции.

где λ_a-b - это длина волны разности разности частот (f_a-f_b) между сигналами L1 и L2

Вычитая уравнение (8) из уравнения (7) и разделив результат на длину волны разности λ_a-b, получаем прямую меру разностной неопределенности как

Аналогичным образом разностные неопределенности в разностях измерений по фазе (L1-L5) и (L2-L5) могут быть определены с помощью уравнений

В некоторых вариантах осуществления предполагается, что и кодовые измерения и измерения по фазе несущей в уравнениях (9)-(11) скорректированы с использованием измерений, выполненных на базовом приемнике. Однако из-за соотношения между частотами только два из трех разностных измерений по фазе несущей являются независимыми. Вследствие этого, как только будет определена разностная неопределенность для любых двух из этих разностей измерений, неопределенность для третьей разности измерений сразу будет определена.

Но до тех пор пока имеется фазовая синхронизация между двумя частотами в разности измерений по фазе несущей, соответствующая разностная неопределенность не будет меняться в процессе времени. Также величина может быть сглажена во времени сходным образом. В некоторых вариантах осуществления процесс сглаживания выполняется расширяющимся средним фильтром

где n представляет степень сглаживания, например, в терминах числа эпох измерений. Степень сглаживания, требуемая для получения корректной неопределенности на большом расстоянии, является функцией от длины волны λ_a-b разности частот. Сглаженное значение разностной неопределенности может быть вставлено в уравнение (8) для получения скорректированного измерения по фазе несущей с вычисленной неопределенностью

Последний член в выражении (13) выше соответствует ошибке ионосферной рефракции в разностном измерении. Затем эта ошибка удаляется в операции 220 способа 200 формированием скорректированного композитного измерения по фазе несущей с вычисленной неопределенностью, используя измерения по фазе несущей, взятые на всех трех частотах, как будет детально объяснено ниже.

Первая операция в удалении этой ошибки ионосферной рефракции - формирование другого разностного измерения по фазе несущей с вычисленной неопределенностью от трех доступных первичных измерений по фазе. В некоторых вариантах осуществления второе разностное измерение по фазе несущей с вычисленной неопределенностью формируется, используя разность измерений по фазе несущей (L2-L5), поскольку для определения точной величины неопределенности на большом расстоянии требуется в среднем меньше времени. Аналогично уравнению (13) это второе разностное измерение по фазе несущей с вычисленной неопределенностью на основе измерений по фазе несущей (L2-L5) может быть определено как

Линейная комбинация уравнений (13) и (14) удаляет ошибку ионосферной рефракции и дает скорректированное композитное измерение Φ_RC по фазе несущей с вычисленной неопределенностью.

К сожалению, вышеупомянутый процесс формирования разностных измерений по фазе несущей с вычисленной неопределенностью и дальнейшего удаления ошибок ионосферной рефракции значительно усиливает шум в первичных измерениях по фазе несущей. Например, из-за того что частоты L2 и L5 столь близки друг к другу (разница между этими частотами составляет лишь 51,15 МГц), вычитание измерений по фазе несущей на двух частотах в уравнении (14) приводит к большому объему многолучевого шума в получающейся разности измерений Φ_bc. После коррекции ионосферной рефракции в уравнении (15) многолучевой шум еще больше усилится.

Более того, поскольку только два из трех разностных измерений по фазе несущей с вычисленной неопределенностью являются независимыми, эффект усиления шума не зависит от того, какие два будут взяты в уравнении (15) для образования скорректированного композитного измерения по фазе несущей с вычисленной неопределенностью. Другими словами, подобные проблемы присутствуют и в других комбинациях разностных измерений по фазе несущей. Фактически это наблюдение становится более наглядным при замене двух разностных измерений Φ_ab и Φ_bc в уравнении (15) на масштабированные измерения по фазе несущей Φ_a, Φ_b и Φ_c, определенные в уравнениях (4)-(6)

(16)

Уравнение (16) определяет характерное соотношение между композитным измерением по фазе несущей и первичными измерениями по фазе несущей на трех частотах. Это соотношение распространяется как на GPS-систему Соединенных Штатов, так и на другие Глобальные Спутниковые Навигационные Системы (GNSS), такие как европейская система Galileo. Фактически GPS-системы и система Galileo имеют одни и те же частоты для сигналов L1 и L5, но разную частоту для сигнала L2. Средняя частота системы Galileo, E6 равна 1278,75 МГц, что на 51,15 МГц выше, чем частота L2.

Уравнение (16) показывает, что частоты несущего сигнала влияют на уровень шума в композитном измерении по фазе несущей Φ_RC. В некоторых вариантах реализации ожидаемый шум в измерении по фазе несущей Φ_RC определяется как квадратный корень из суммы квадратов шумов в первичных измерениях по фазе несущих, каждый шум взвешен ассоциированными с ним коэффициентами в уравнении (16). Таблица 1 предоставляет значения коэффициентов в уравнении (16) под различными средними частотами (GPS L2, Galileo E6 и 1,3299 ГГц) и соответствующие уровни шума в предположении, что имеется одинаковый шум в один сантиметр от каждого из трех несущих сигналов.

Таблица 1Усиление односантиметрового шума
Средняя частота	C1	C2	C3	RSS
GPS L2	17,89	-84,71	67,82	109,98
Galileo E6	20,97	-53,88	33,91	67,03
1,3299 ГГц	25,34	-46,94	22,61	57,94

Очевидно, переход от сигнала GPS L2 к сигналу Galileo E6 как средней частоте снижает шум приблизительно на 39% ≈ (109,98-67,03)/109,98. Это наводит на мысль, что сигнал Galileo E6 лучше, чем GPS-сигнал L2, подходит для минимизации шума в скорректированных разностных измерениях по фазе несущей с вычисленной неопределенностью.

Хотя шум усиливается в скорректированных композитных разностных измерениях Φ_RC по фазе несущей с вычисленной неопределенностью, все же он выдерживает сравнение с уровнем шума в скорректированном композитном кодовом измерении. Это вызвано, по меньшей мере, частично тем, что измерения по фазе несущей меньше, чем кодовые измерения, подвержены негативным влияниям от различных источников, таких как свойства дизайна приемника. Далее композитные измерения по фазе несущей менее чувствительны к завершению фазы из-за равного количества положительных и отрицательных измерений по фазе в композитном измерении. Большая часть шума в композитных измерениях по фазе Φ_RC возникает из-за помех типа "повторное изображение", имеющегося в отдельных первичных измерениях по фазе несущей. К счастью, тот же самый метод, примененный для сглаживания многолучевого распространения в кодовых измерениях, может быть использован для сглаживания помех от многолучевого распространения в композитном измерении по фазе несущей.

Для уменьшения шума многолучевого распространения способ 200 включает в себя операцию 230, в которой формируется скорректированное композитное измерение по фазе несущей с минимальным шумом, и операцию 240, в которой скорректированное измерение по фазе несущей с вычисленной неопределенностью уравнения (16) сглаживается скорректированным композитным измерением по фазе несущей с минимальным шумом. Обратите внимание, что нет требования к решению неопределенности в скорректированном композитном измерении по фазе несущей с минимальным шумом, сформированном в операции 230. Другими словами, композитное измерение по фазе несущей может включать в себя ошибку, относящуюся к неопределенности.

Аналогично уравнению (16) скорректированное композитное измерение Φ_M по фазе несущей с минимальным шумом определяется как функция от трех масштабированных первичных измерений по фазе несущей Φ_a, Φ_b, и Φ_c

где a, b и c - коэффициенты для умножения масштабированных первичных измерений по фазе несущей на трех частотах. Подстановка определения трех масштабированных первичных измерений по фазе несущей в уравнениях (4)-(6) в уравнение (17) превращает уравнение (17) в новую форму

Для иллюстративных целей предположим, что каждое из этих трех масштабированных первичных измерений по фазе несущей имеет шум в один сантиметр. Для того чтобы композитное измерение Φ_M достигло минимума, коэффициенты a, b и c должны удовлетворять следующим трем ограничениям:

Уравнение (19) показывает, что выбор коэффициентов не увеличивает и не уменьшает расстояние. Уравнение (20) показывает, что из композитного измерения удалена ошибка ионосферной рефракции. Уравнение (21) показывает, что для определенных коэффициентов имеется минимальное усиление шума. Обратите внимание, что если предположение равного шума неверно, например в трех измерениях по фазе несущей имеются неравные шумы, то уравнение (21) должно быть соответствующим образом модифицировано.

Решение уравнения (19) для с дает:

Подстановка уравнения (22) в уравнение (20) и решение его для b дает:

это выражение в свою очередь может быть упрощено до:

Заменяя c и b в уравнении (21) уравнениями (22) и (24) соответственно, получаем:

Взяв производную по a, приравняв производную к нулю и решив уравнение, получаем:

Значения b и c могут быть получены подстановкой уравнения (26) обратно в уравнения (24) и (22) соответственно. Числовые значения коэффициентов a, b и c, полученные выше под тремя различными средними частотами, показаны в Таблице 2.

Таблица 2Коэффициенты для коррекции на рефракцию с минимумом шума
Средняя частота	a	b	c	RSS=
GPS L2	2,3269	-0,3596	-0,9673	2,546
Galileo E6	2,2691	-0,0245	-1,2446	2,588
1,3299 ГГц	2,1065	0,3135	1,4200	2,560

Последняя колонка Таблицы 2 оценивает усиление шума в первичных измерениях по фазе несущей. В отличие от результата в Таблице 1 GPS-частота L2 в действительности дает несколько меньший скорректированный на рефракцию шум (2,546), чем частота Galileo E6 (2,588), если отсутствует первичная неопределенность в композитном измерении по фазе несущей Φ_М.

Фиг.3 иллюстрирует процесс 300 сглаживания в операции 240 в соответствии с некоторыми из вариантов осуществления настоящего изобретения. Как отмечено выше, и композитное измерение по фазе несущей Φ_RC в уравнении (16), и композитное измерение Φ_M в уравнении (17) содержат измерения скорректированного на рефракцию геометрического расстояния. Таким образом, вычисляя разность двух композитных измерений, получаем величину коррекции, равную 0 (операция 310), как функцию шума многолучевого распространения в трех частотах и постоянной ошибки смещения, вызванной первичными неопределенностями в уравнении (17)

После сглаживания расширяющимся средним фильтром (операция 320) величина коррекции приблизится к отрицательному значению постоянной ошибки смещения в уравнении (17). В некоторых вариантах осуществления сглаженная коррекция задается с помощью

где значение n увеличивается на единицу с каждой эпохой измерения.

В конечном итоге сглаженное значение смещения S_n добавляется обратно в скорректированное композитное измерение Φ_M по фазе несущей с минимальным шумом (операция 330), чтобы получить в большей степени точное скорректированное композитное измерение по фазе несущей с минимальным шумом без смещения. В некоторых вариантах осуществления сглаженное скорректированное измерение Φ_s по фазе несущей с вычисленной неопределенностью определяется формулой

Одним из преимуществ использования операций 320 и 330 в процессе 300 для сглаживания измерений по фазе несущей с вычисленной неопределенностью является возможность контроля корректности величины коррекции в процессе сглаживания.

Следует обратить внимание, что шум в первичных измерениях по фазе несущей не является белым. Наоборот, на него воздействуют эффекты многолучевого распространения, являющиеся цветным шумом. Таким образом, реальный средний тренд шума в уравнении (29) зависит от автокорреляции шумов многолучевого распространения и измерений приемника. В некоторых вариантах осуществления начальная положительная автокорреляция приводит к более медленному усреднению действительного шума, чем белого шума. Через несколько минут, когда автокорреляция становится отрицательной, действительный шум усредняется быстрее, чем белый шум.

Необходимо также заметить, что в отличие от эффектов многолучевого распространения в кодовых измерениях, многолучевое распространение в измерениях по фазе несущей имеет равное распределение положительной и отрицательной ошибок и должно сходиться к нулю с течением времени. В результате необходимо ожидать того, что остаточный шум будет составлять несколько сантиметров через 15-30 минут сглаживания.

Поскольку ни одно из трех композитных разностных измерений по фазе несущей с вычисленной неопределенностью не может быть выведено из двух других измерений, имеется только одна степень свободы для неопределенностей фазы, имеющихся в трех первичных измерениях по фазе несущей. Другими словами, ограниченная корректными величинами разностных неопределенностей, любая ошибка оценки в величине одной из неопределенностей фазы приведет к равной ошибке в остальных величинах первичных неопределенностей фазы. Например, если неопределенность фазы N в уравнении (4) оказывается на один полный цикл больше, чем истинное значение, то обе неопределенности фазы N_b и N_c будут на один полный цикл больше, чем их истинные значения, в предположении, что неопределенности разностных измерений (N_a-N_b) и (N_a-N_c) в уравнениях (9) и (10) были определены верно.

Таблица 3 ниже дает расчетную скорректированную на рефракцию длину волны λ_RC композитного измерения Φ_M при соответствующих средних частотах. Эта длина волны λ_RC является по существу ошибкой оценки дальности, вызванной ошибкой неопределенности фазы в каждом из трех первичных измерений по фазе. Как показано ниже в Таблице 3, ошибка оценки дальности составляет приблизительно 11 сантиметров (все длины волн показаны в метрах).

Таблица 3Длины волн, скорректированных на рефракцию
Средняя частота	aλa	bλb	сλс	λRC =aλa+bλb+c?c
GPS L2	0,4428	-0,0878	-0,2465	0,1085
Galileo E6	0,4318	-0,0058	-0,3172	0,1089
1,3299 ГГц	0,4008	0,0707	-0,3619	0,1097

Как отмечено ранее, скорректированное композитное измерение Φ_M по фазе несущей с минимальным шумом может включать в себя постоянную ошибку, связанную с неопределенностью. Однако скорректированное композитное разностное измерение Φ_RC по фазе несущей с вычисленной неопределенностью не зависит от любых ошибок, связанных с неопределенностью в первичных измерениях по фазе несущей. Соответственно, разность между двумя композитными измерениями по фазе, как это представлено уравнениями с (27) по (29), будучи разделенная на скорректированную на рефракцию длину волны λ_RC (последняя колонка в Таблице 3) и округленная до ближайшего целого, оценивает величину ошибки неопределенности фазы ΔN в первичных измерениях по фазе, т.е.

Добавление ошибки неопределенности фазы ΔN к начальной оценке трех первичных неопределенностей фазы N_a, N_b и N_c дает более точные значения этих трех первичных неопределенностей фазы,

Подставив эти точные величины неопределенностей обратно в уравнение (17), мы сможем выразить скорректированное композитное измерение Φ_AR по фазе несущей с минимальным шумом и вычисленной неопределенностью как

(34)

Композитное измерение Φ_AR в уравнении (34) сходно с композитным измерением Φ_s в уравнении (29). Однако поскольку первичная ошибка неопределенности кратна полному циклу, округление до ближайшего целого в уравнении (30) делает композитное измерение Φ_AR более точным, чем композитное измерение Φ_s.

Как показано в уравнениях (4)-(6), три масштабированных первичных измерения Φ_a, Φ_b, и Φ_c являются функциями геометрического расстояния ρ, эффекта ионосферной рефракции I и шума. В одном из вариантов осуществления три первичных измерения могут быть скомбинированы в одно выражение (например, уравнение (16)) для удаления эффекта I ионосферной рефракции, оставляя только геометрическое расстояние ρ и шум. В другом варианте осуществления три первичных измерения могут быть объединены в другое выражение для удаления эффекта I ионосферной рефракции, оставляя только геометрическое расстояние ρ и шум. Вставив эти два выражения в уравнения (4)-(6), мы удалим и геометрическое расстояние ρ, и эффект I ионосферной рефракции, получив масштабированную комбинацию шума в трех первичных измерениях.

Имеются другие способы генерации масштабированных комбинаций шума. В некоторых вариантах осуществления масштабированная комбинация шума получается генерацией двух представлений для эффекта I ионосферной рефракции, с помощью различных комбинаций первичных измерений и затем взятия разности двух представлений. В некоторых других вариантах осуществления масштабированная комбинация шума получается генерацией двух представлений для расстояния ρ, с помощью различных комбинаций первичных измерений и затем взятия разности двух представлений. В некоторых других вариантах осуществл