Способ пороговой генерации ключей для системы защиты информации на основе идентификационных данных

Способ пороговой генерации ключей для системы защиты информации на основе идентификационных данных

Иллюстрации

Показать все

Реферат

Изобретение относится к способам защиты информации, а более конкретно к алгоритмам управления ключами для систем с открытым ключом. Изобретение может найти применение в способах распределения ключей для узлов (т.е. компьютеров с сетевыми интерфейсами) вычислительной сети.

Отличительной чертой известной из уровня техники системы защиты информации на основе идентификационных данных (СЗИОИД) является возможность использования в качестве открытого ключа уникального идентификатора узла (любой строки, например, электронного адреса someone@somehost.com). В отличие от традиционных систем защиты информации с открытым ключом в СЗИОИД узлу-отправителю не нужно получать открытый ключ узла-получателя и его сертификат, так как данный ключ может быть получен из уникального идентификатора узла-получателя. Таким образом, в СЗИОИД не требуется наличия доверенного центра сертификации, хранящего открытые ключи всех узлов сети и их сертификаты. В то же время для данной схемы требуется другой доверенный центр, а именно - генератор секретных ключей (ГСК), который генерирует секретные ключи узлов на основе их идентификаторов и секретного мастер-ключа. Главным достоинством СЗИОИД является то, что узлу-отправителю не нужно запрашивать открытый ключ узла-получателя, а серьезным недостатком является то, что ГСК представляет собой наиболее уязвимую часть системы. Если ГСК будет компрометирован, и секретный мастер-ключ будет раскрыт, то все ранее выданные секретные ключи тоже будут раскрыты. Если ГСК будет недоступен, то новый узел не сможет присоединиться к сети, т.к. не сможет получить свой секретный ключ. Было предложено несколько реализаций СЗИОИД, которые используют разный математический аппарат (см., например, [4], [5], где используются эллиптические кривые, и [1], [2], где используются вычеты).

Из уровня техники известна также пороговая система защиты информации на основе идентификационных данных (ПСЗИОИД), которая была разработана для устранения вышеупомянутых недостатков СЗИОИД. В данной системе любая коалиция из определенного количества узлов сети может выступать в роли ГСК. Пусть в сети есть l узлов, которые могут принимать участие в организации ГСК, тогда любая коалиция из k (k≤1) этих узлов может совместно генерировать секретные ключи для других узлов. Однако, при этом ни один из ее участников не имеет полной информации ни о секретном мастер-ключе системы, ни о сгенерированных секретных ключах. Ключевой идеей ПСЗИОИД является разделение секретного мастер-ключа между всеми l узлами системы. Выдача секретного ключа новому узлу происходит следующим образом. Новый узел выбирает коалицию из k узлов ГСК и посылает им запрос. Все узлы ГСК по отдельности производят частичные вычисления со своей тенью секретного мастер-ключа и идентификатором узла, а затем отсылают узлу свои результаты (тени секретного ключа узла). Узел комбинирует присланные тени и получает собственный секретный ключ.

Таким образом, протокол работы ПСЗИОИД включает в себя следующий набор операционных этапов.

Этап 1 - Начальная инициализация (l, k, σ). Алгоритм, на вход которого поступает количество узлов l, которые могут использоваться как участники ГСК, порог k (1≤k≤l), и параметр криптостойкости σ. На выходе алгоритм выдает (РК, VK, SK), где РК - открытый ключ системы, VK - проверочный ключ, SK=(SK₁, …, SK_l) - набор теней секретного мастер-ключа системы. Узлу с номером i выдается тень (i, SK_i).

Этап 2 - Генерация теней секретного ключа и проверок к ним (РК, VK, i, SK_i, ID). Алгоритм, на вход которого поступает открытый ключ системы РК, проверочный ключ VK, идентификатор узла ID и тень секретного мастер-ключа (i, SK_i). На выходе алгоритм выдает тень секретного ключа узла (i, H_i), а также проверку для этой тени Р_i.

Этап 3 - Проверка теней секретного ключа и вычисление секретного ключа по теням (РК, VK, ID, (H₁, …, H_k), (P₁, …, P_k)). Алгоритм, на вход которого поступает открытый ключ системы РК, проверочный ключ VK, идентификатор ID, тени секретного ключа (H₁, …, H_k) и проверки для них (P₁, …, P_k). С помощью проверок узел может проверить правильность присланных ему теней, а затем, объединив тени, получить на выходе свой секретный ключ d_ID.

Этап 4 - Шифрование (РК, ID, М). Алгоритм, на вход которого поступает открытый ключ РК, идентификатор ID, сообщением. На выходе алгоритм выдает шифртекст С.

Этап 5 - Дешифрование (РК, ID, d_ID, С). Алгоритм, на вход которого поступает открытый ключ РК, идентификатор ID, секретный ключ d_ID, шифртекст С. На выходе алгоритм выдает сообщение М.

Все известные варианты реализации ПСЗИОИД используют аппарат эллиптических кривых (см. [6], [7]), который значительно превосходит по вычислительной сложности арифметику вычетов. То есть все известные к настоящему времени решения имеют существенный недостаток, заключающийся в чрезвычайно высокой вычислительной сложности, требующей применения дорогостоящей аппаратуры или занимающей много времени.

В технической литературе упоминаются системы ПСЗИОИД (см. [6], [7]), построенные с использованием аппарата эллиптических кривых для СЗИОИД (см. [4], [5]) того же типа. Однако известны также системы СЗИОИД (система Кокса [1] и система Бонэ [2]), построенные с использованием аппарата теории чисел (арифметика вычетов и квадратичных вычетов). По сравнению с системами на эллиптических кривых такие системы обладают меньшей сложностью шифрования и дешифрования. Система Кокса [1] выбрана в качестве прототипа заявляемого изобретения. Заметим, что ПСЗИОИД для системы Бонэ [2] может быть построена аналогичным образом.

Поскольку пороговой схемы для прототипа [1] не было разработано, то задача, на решение которой направлено заявляемое изобретение, состоит в создании пороговой схемы (ПСЗИОИД), обеспечивающей повышение отказоустойчивости и безопасности ГСК для СЗИОИД, использующей арифметику вычетов и обеспечивающей более низкую сложность операций шифрования и дешифрования по сравнению с известными из уровня техники решениями.

Таким образом, в заявляемом изобретении для создания ПСЗИОИД в прототип (СЗИОИД Кокса [1]) вносятся новые признаки (операции), заключающиеся в том, что в процессе начальной инициализации (Этап 1) вычисляют секретный (мастер-ключ), проверочный и открытый ключи системы, разбивают мастер-ключ на тени для каждого узла, который имеет возможность быть участником ГСК, затем в ответ на запрос нового узла на выдачу секретного ключа узлы, входящие в коалицию, образующую ГСК (Этап 2), вычисляют тени секретного ключа и проверки для них, которые посылаются узлу, запросившему секретный ключ (Этап 3), который проверяет тени с помощью проверок и объединяет эти тени, получая свой секретный ключ. Иными словами, в заявляемом изобретении предлагаются оригинальные алгоритмы для этапов 1, 2 и 3, приведенных на прилагаемых чертежах.

Задача изобретения решается за счет использования при построении ПСЗИОИД модификации распределенной подписи Шоупа (см. [3]). Оригинальная схема Шоупа предназначена для порогового разделения секретного ключа в схеме RSA с отрытым ключом и не предусматривает использования в СЗИОИД (RSA - это буквенная аббревиатура от фамилий Rivest, Shamir и Adieman, ассоциирующаяся с понятием "алгоритм с открытым ключом"). Ниже приводится краткое описание схемы Шоупа.

При начальной инициализации вычисляют модуль M=p·q, где р=2р'+1 и q=2q'+1 --- сильные простые. Пусть m=p'·q', тогда функция Эйлера ϕ(М)=4m. Затем генерируют открытый ключ е и вычисляют секретный ключ d: d·e≡1 mod m. Для разделения ключа d по схеме разделения секрета Шамира генерируют многочлен , коэффициенты f_i (1≤i≤k-1) выбирают случайным образом из диапазона {0, …, m-1}. Тени секретного ключа для i-го узла вычисляют по формуле SK_i=f(i) mod m.

При генерации теней подписи каждый узел-участник коалиции вычисляет тень где g=hash(Message) mod M и Δ=l!, и отсылает ее узлу, запросившему подпись.

При вычислении подписи по теням вычисляют где и i, j∈{0…l}, a S --- множество идентификаторов узлов, входящих в коалицию. Из ω подпись r вычисляют как где и b - решения уравнения

Предлагаемая модификация описанной выше подписи Шоупа заключается в следующих изменениях:

• при начальной инициализации:

- секретный мастер-ключ представляют в виде суммы d=4·d₁+d₂;

- генерируют тени для обоих компонентов суммы и выдают каждому узлу ГСК две тени и ;

- публикуют открытый ключ системы PK=(M, x, y), где x и y такие, что 4d₂x+y≡d₂ mod ϕ(М);

• при генерации теней секретного ключа для нового узла:

- от каждого узла из выбранной коалиции узлов, образующих ГСК, новому узлу посылают две тени его секретного ключа

• при вычислении секретного ключа по теням:

- вычисляют секретный ключ нового узла по теням следующим образом:

Далее существо заявляемого изобретения, а именно ПСЗИОИД, основанная на СЗИОИД Кокса [1] и алгоритме распределенной подписи Шоупа [3], поясняется в деталях с привлечением графических материалов, где

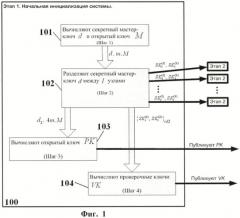
Фиг.1. Схема пошагового выполнения этапа начальной инициализации системы.

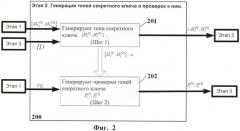
Фиг.2. Схема пошагового выполнения этапа генерации теней секретного ключа и проверок к ним.

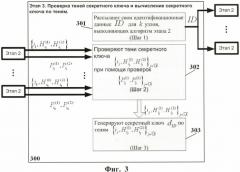
Фиг.3. Схема пошагового выполнения этапа проверки теней секретного ключа и вычисления секретного ключа по теням.

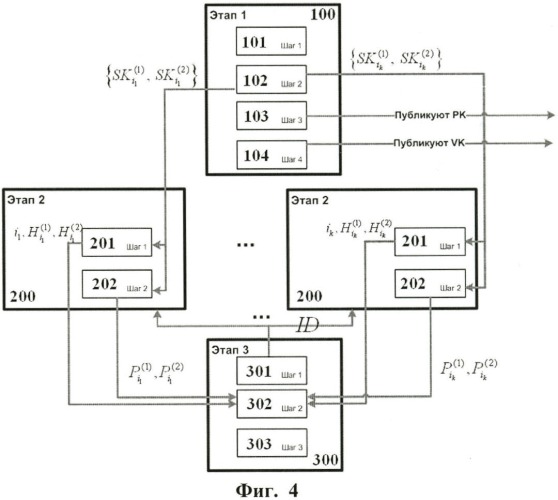
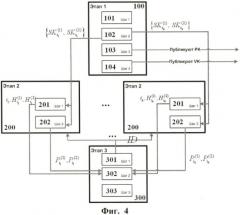
Фиг.4. Схема взаимодействия предложенных в изобретении этапов системы.

Рассмотрим основные этапы работы ПСЗИОИД.

Этап 1 (100 на Фиг.1). Начальная инициализация. Шаги алгоритма, выполняемого на данном этапе, показаны на Фиг.1. Администратор системы генерирует необходимые ключи и инициализирует ими узлы, которые могут быть участниками ГСК.

Шаг 1 (101 на Фиг.1). Вычисление секретного мастер-ключа d (данный шаг, в частности, описан в работе Кокса [1]). Выбирают два сильных простых числа р=2р'+1 и q=2q'+1 и вычисляют модуль криптосистемы М=pq. Пусть m=p'·q', тогда ϕ(М)=4·m, а секретный мастер-ключ равен .

Шаг 2 (102 на Фиг.1). Разделение секретного мастер-ключа d между l узлами (данный шаг является оригинальным). Секретный мастер-ключ представляют в виде суммы d=4·d₁+d₂ и, используя схему разделения секрета Шамира, разделяют d₁ и d₂ между l узлами-участниками. Для этого генерируют случайный полином f(x) по модулю m степени k-1 такой, что f(0)=d₁, и случайный полином g(x) по модулю m степени k-1 такой, что g(0)=d₂. Затем каждому узлу сообщают две тени и , где 1≤i≤l и Δ=l!.

Шаг 3 (103 на Фиг.1). Вычисление открытого ключа (данный шаг является оригинальным). Открытым ключом системы является модуль М и два числа x и y такие, что 4d₂x+y≡d₂ mod ϕ(М). Числа x и y вычисляют следующим образом: выбирают случайное x<m-1, затем у вычисляют по формуле y=d₂(1-4x) mod ϕ(М). Итак, открытый ключ системы состоит из 3 чисел: РК=(М, x, y). Этот ключ публикуют для общего доступа.

Шаг 4 (104 на Фиг.1). Вычисление проверочных ключей (данный шаг описан, в частности, в работе Шоупа [3]). Выбирают случайную величину v из подгруппы квадратичных вычетов в Z_M и для 1≤i≤l вычисляют проверочные ключи и . Проверочный ключ системы состоит из следующих чисел: Этот ключ публикуют для общего доступа.

Этап 2 (200 на Фиг.2). Генерация теней секретного ключа и проверок к ним. Шаги алгоритма, выполняемого на данном этапе, показаны на Фиг.2. Этот этап выполняется каждым узлом из коалиции узлов, образующих ГСК, в ответ на запрос нового узла о выдаче ключа. Запрос содержит идентификатор ID нового узла.

Шаг 1 (201 на Фиг.2). Генерация теней секретного ключа (данный шаг является оригинальным). Получив от нового узла (этап 3) запрос на выдачу секретного ключа, вычисляют две тени его секретного ключа, используя тени секретного мастер-ключа, следующим образом: Затем посылают новому узлу набор {i, , }.

Шаг 2 (202 на Фиг.2). Генерация проверок (данный шаг описан, в частности, в работе Шоупа [3]). Для проверки тени можно проверить, что дискретный логарифм по основанию равен дискретному логарифму ν_i по основанию ν. Для этого шага в системе используют следующий алгоритм. Вместе с тенью секретного ключа узлу посылают и проверку для нее, которую вычисляют по следующему алгоритму. Пусть L() --- функция, возвращающая длину в битах своего параметра. Пусть H' --- хэш-функция, выдающая на выходе L₁-битные целые числа, где L₁ --- параметр криптостойкости. При создании проверки для тени секретного ключа узла выбирают случайное число и вычисляют

Таким образом, проверкой для тени является пара .

Проверку для тени вычисляют аналогичным способом.

Этап 3 (300 на Фиг.3). Проверка теней секретного ключа и вычисление секретного ключа по теням. Шаги алгоритма, выполняемого на данном этапе, показаны на Фиг.3. В ответ на свой запрос о выдаче секретного ключа новый узел получает от узлов, входящих в состав ГСК, тени секретного ключа и проверки для них.

Шаг 1 (301 на Фиг.3). Запрос секретного ключа. Рассылают запросы о выдаче секретного ключа коалиции из узлов, входящих в состав ГСК, алгоритм работы которых представлен на Фиг 2.

Шаг 2 (302 на Фиг.3). Проверка теней секретного ключа (шаг предложен, в частности, в работе Шоупа [3]). Получив от узлов, входящих в состав ГСК (этап 2), тени и их проверки, проверяют для всех теней и проверок, что

Для проверяют аналогичное соотношение.

Шаг 3 (303 на Фиг.3). Вычисление секретного ключа по теням (данный шаг является оригинальным). Без потери общности будем считать, что узлы, входящие в состав ГСК и образующие коалицию S, имеют номера l, …, k, тогда λ_0,1, …, λ_0,k --- коэффициенты Лагранжа узлов из коалиции S, a λ'_0,1=Δ·λ_0,1, …, λ'_0,k=Δ·λ_0,k∈Z_m --- модифицированные коэффициенты Лагранжа, такие что . Тогда секретный ключ вычисляют следующим образом:

Этап 4. Шифрование (этап предложен, в частности, в работе Кокса [1]).

При шифровании одного бита x, где x∈{-1, 1} для передачи узлу с идентификатором ID, вычисляют открытый ключ этого узла как генерируют случайные числа t₁ и t₂, для которых выполняется , и вычисляют S₁ и S₂:

Тогда шифр-текстом будет являться С=<S₁, S₂>.

Этап 5. Дешифрование (этап предложен в работе Кокса [1]).

Дешифрование шифр-текста C=<S₁, S₂> осуществляют с помощью секретного ключа d_ID следующим образом:

Что касается взаимодействия алгоритмов, реализующих этапы (1) 100, (2) 200 и (3) 300 на Фиг.4, то подразумевается, что на шаге 101 этапа 100 генерируют секретный мастер-ключ, на шаге 102 генерируют его тени, которые посылают на вход алгоритму этапа 200. На шаге 103 генерируют открытый ключ, который публикуют для общего доступа. На шаге 104 генерируют проверочный ключ, который также публикуют для общего доступа. На этапе 200, получив от алгоритма, реализующего этап 300, запрос на выдачу секретного ключа, на шаге 201 генерируют тени секретного ключа и отправляют их алгоритму, реализующему этап 300. Затем на шаге 202 вычисляют проверки для теней и отправляют в адрес алгоритма, реализующего этап 300. На шаге 301 этапа 300 отсылают запрос на получение секретного ключа коалиции из узлов, выполняющих алгоритм, реализующий этап 200. Затем на шаге 302, приняв тени и проверки для них, проверяют тени. На шаге 303 вычисляют секретный ключ по теням.

Промышленная применимость

Заявляемое изобретение может применяться для повышения отказоустойчивости и безопасности генератора секретных ключей в системах защиты информации на основе идентификационных данных. Алгоритмы, реализующие этапы предлагаемого изобретения, могут быть реализованы как в виде программного обеспечения для универсального компьютера любой архитектуры, так и в виде аппаратного обеспечения для специализированного компьютера любой архитектуры.

Ссылки

1. C.Cocks, "An Identity Based Encryption Scheme based on Quadratic Residues", 2001, LNCS, vol.2260, pp.360-363.

2. D.Boneh, C.Gentry, M, Hamburg, "Space-Efficient Identity Based Encryption Without Pairings", In proceedings of FOCS'07, 2007, pp.647-657.

3. V.Shoup, "Practical threshold signatures", In proceedings EUROCRYPT'00, 2000, LNCS, vol.1807, pp.207-220.

4. D.Boneh, M.Franklin, "Systems and methods for identity-based encryption and related cryptographic techniques", US patent application 20030081785, Boneh, Dan (Palo Alto, CA, US), Franklin, Matthew (Davis, CA, US), 2003, May.

5. D.Boneh, X.Boyen, "Identity-based-encryption system", US patent 7590236, Boneh, Dan (Palo Alto, CA, US), Boyen, Xavier (Palo Alto, CA, US), 2009, September.

6. D.Boneh, X.Boyen, S.Halevi, "Chosen Cipher-text Secure Public Key Threshold Encryption Without Random Oracles", CTRSA'06, 2006, pp.226-243.

7. J.Li, Y.Wang, "Threshold Identity Based Encryption Scheme without Random Oracles", WCAN'06, 2006.

1. Способ пороговой генерации ключей для системы защиты информации на основе идентификационных данных с использованием модификации распределенной подписи для порогового разделения секретного ключа в схеме алгоритма с открытым ключом (RSA), отличающийся тем, чтопри начальной инициализации:секретный мастер-ключ представляют в виде суммы d=4·d₁+d₂;генерируют тени для обоих компонентов суммы и выдают каждому узлу, образующему генератор секретных ключей (ГСК), две тени и ;публикуют открытый ключ системы РК=(М,x,y), где x и y такие, что 4d₂x+y≡d₂ mod ϕ(М);при генерации теней секретного ключа нового узла:от каждого узла из выбранной коалиции узлов, образующих ГСК, новому узлу посылают две тени секретного ключа узла где при вычислении секретного ключа по теням:вычисляют секретный ключ узла по теням следующим образом:

2. Способ по п.1, отличающийся тем, что на этапе начальной инициализации секретный мастер-ключ d представляют в виде суммы d=4·d₁+d₂ и каждому i-му узлу, входящему в состав ГСК, сообщают две компоненты тени и , где 1≤i≤l и Δ=l! и f(x), g(x) - случайные полиномы по модулю m степени k-1 такие, что f(0)=d₁, g(0)=d₂, а открытым ключом системы становится М и два числа x и y, такие, что 4d₂x+y≡d₂ mod ϕ(М).

3. Способ по п.2, отличающийся тем, что на этапе генерации теней секретного ключа узла, входящего в состав ГСК, две тени секретного ключа узла определяют из соотношений где

4. Способ по п.1, отличающийся тем, что на этапе вычисления секретного ключа секретный ключ узла вычисляют по теням следующим образом: