Способ автономной навигации и ориентации космических аппаратов на основе виртуальных измерений зенитных расстояний звезд

Способ автономной навигации и ориентации космических аппаратов на основе виртуальных измерений зенитных расстояний звезд

Иллюстрации

Показать все

Реферат

Изобретение относится к бортовой системе управления космическими аппаратами для автономной (не зависящей от наземного комплекса управления - НКУ) оценки орбиты и ориентации корпуса КА.

Известны два способа автономной навигации, применяемые на беспилотных КА. Первый способ был реализован на аппаратах 11 Ф624. Он включал в себя измерение зенитных расстояний двух звезд с помощью двух астровизирующих устройств (АВУ) и радиотехнического построителя местной вертикали. Дополнительно для измерения высоты полета построитель местной вертикали снабжался еще одним приемопередающим устройством. Этот способ описан в книге "Математическое и программное обеспечение системы автономной навигации КА 11 Ф624", под редакцией Ю.Г.Антонова и С.И.Маркова, МО СССР, 1986 г.

Второй способ заключается в компьютерном расчете положения в трехмерном пространстве орта радиус-вектора опорной (расчетной, априори полагаемой) орбиты, жестком закреплении оптико-электронных приборов на корпусе КА и измерении в них координат и яркости звезд, попавших в поле зрения в моменты навигационных сеансов. Это позволило увеличить число и точность решаемых задач, расширить возможности среды применения способа для любых орбит, уменьшить количество измерительных приборов и массогабаритные характеристики бортовой системы управления КА. Этот способ описан в статье "Метод автономной астрономической навигации и ориентации ИСЗ", авторы: Кузнецов В.И., Смолицкий Х.Л.., Данилова Т.В. Известия вузов. Приборостроение, 2003. Т.46. N24. С.5-16 и патенте РФ на изобретение RU 2318188 С1 "Способ автономной навигации и ориентации космических аппаратов", приоритет изобретения 17 июля 2006 г., авторы: Кузнецов В.И и Данилова Т.В.

Наиболее близким по технической сущности к заявляемому изобретению следует считать второй способ, основанный на виртуальных измерениях зенитных расстояний звезд, который принят за прототип.

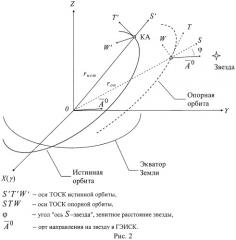
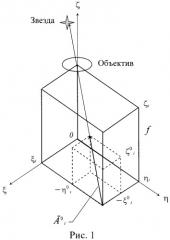
Суть этого способа заключается в том, что измерительная информация поступает только от жестко закрепленных на корпусе спутника ОЭП (их в этом случае достаточно 3). Тогда координаты звезд в фокальной плоскости прибора (см. рис.1) ξ_i и η_i, во-первых, косвенно содержат информацию о местонахождении КА (если с помощью их рассчитать угол между направлением на звезду и каким-либо направлением, связанным с орбитальным движением, например, направлением на центр Земли) и, во-вторых, в этих координатах содержится информация о расхождении трехгранников, связанных с одной стороны с корпусом спутника и с другой - с текущей орбитальной системой координат (ТОСК). Последняя, в свою очередь, связана с местонахождением КА (см. рис.2, где ТОСК представлена системой STW, S -по радиус-вектору орбиты, Т - по трансверсали, W - по бинормали). Поэтому при жестко закрепленных ОЭП возможно решить одновременно и задачу навигации, и задачу ориентации.

Основой ветви алгоритма, определяющей орбиту, является расчет угла φ между направлением на звезду и осью S в координатах ТОСК. По сути, этот угол есть зенитное расстояние звезды, а расчет его на основе измеренных ξ_i и η_i можно представить как виртуальные измерения зенитного расстояния и использовать в качестве измеряемого параметра для решения навигационной задачи в геоцентрической экваториальной инерциальной системе координат (ГЭИСК).

Задача ориентации решается, используя непосредственно значения ξ_i и η_i.

Для решения обеих задач требуется распознавание звезд, попавших в поле зрения ОЭП, прежде всего для идентификации самой яркой из них (рабочей звезды), а для повышения точности решения (поскольку оценка орбиты зависит от определения углов ориентации и наоборот) - разработки специальных программных мер.

Был разработан циклический режим расчетов, два способа мгновенной оценки углов ориентации в каждом навигационном сеансе (алгоритмы 1 и 2) и два способа распознавания звезд: по яркости, по яркости и угловым расстояниям между звездами. В результате распознавания определяется орт звезды в ГЭИСК, а затем решается навигационная задача как, если бы мы фактически измеряли зенитное расстояние звезды.

Отметим, однако, что достигаемая модельная точность такого алгоритма не может удовлетворить современным требованиям знания своей орбиты для некоторых КА, например, для аппаратов системы ГЛОНАСС.

Целью данного изобретения является дальнейшее повышение точности решения задач навигации и ориентации с использованием виртуальных измерений зенитных расстояний звезд без увеличения количества требуемых ОЭП.

Поэтому технический результат, отмеченный в патенте RU 2318188 С1, а именно: увеличение числа решаемых задач, расширение среды применения способа для любых орбит, уменьшение количества измерительных приборов и массогабаритных характеристик бортовой системы управления, сохраняется и в предполагаемом изобретении.

Предложенный способ разработан на основе различного крепления ОЭП по отношению к корпусу спутника. Он строится на информации от ОЭП в кардановом подвесе (минимум два) и минимум одного жестко закрепленного ОЭП. В этом случае ОЭП в кардановом подвесе, визирующие звезды, будут независимо от колебания корпуса КА точнее определять орбиту, на основании которой будут точнее определяться и углы ориентации. Но при этом возникает существенный вопрос: какие звезды выбрать для визирования?

Очевидно, что наибольшая точность определения орбиты получается при визировании наиболее ярких звезд небесной сферы (звездные величины которых меньше или приблизительно равны 1 и Полярная звезда). Их яркость и редкость в пространстве позволяют достичь высокой надежности и точности визирования. Одновременно они настолько удачно располагаются (всего двадцать звезд), что для любых орбит КА, рассмотренных нами, позволяют оптимизировать их выбор по критерию близости к осям ТОСК. Эти звезды нами названы навигационными.

Выбор с учетом положений Солнца и Луны одной навигационной звезды близко к полюсу опорной орбиты, другой близко к ее плоскости создает надежные условия повышения точности оценок орбиты.

Алгоритм решения навигационной задачи заключается в следующем.

В каждом навигационном сеансе на основе опорной орбиты осуществляется оптимизация выбора навигационных звезд из заданного поля. При визировании навигационной звезды определяется орт оси ОЭП в связанной системе координат по информации датчиков углов карданова подвеса.

В начале расчетов, когда неизвестны погрешности ориентации, их полагают нулевыми, поэтому орт звезды непосредственно переводят в орт звезды в ТОСК c учетом различного порядка наименования осей связанной и текущей систем координат:

После выработки углов ориентации формируют матрицу МП2. Тогда:

где МП2 - матрица перехода от связанной к ТОСК опорной орбиты. Одна из возможных приближенных форм этой матрицы, удобная для дифференцирования:

где υ - угол тангажа;

ψ - угол рыскания;

γ - угол крена.

Из рис.2 ясно, что, если искомый угол φ определять в ГЭИСК, то различное пространственное положение осей S' и S приведет к погрешности расчета измеряемой величины. Если же расчет φ осуществить в ТОСК, то очевидно: как в системе S'W'T', так и в системе STW орты соответствующих осей S⁰, T⁰, W⁰ будут состоять из единиц и нулей.

Например, орт запишется (1,0,0). Поэтому косинус угла между этой осью и направлением на звезду i (ее зенитное расстояние) будет в точности равен соответствующей координате орта например:

При этом, к какой орбите - опорной или истинной - отнести угол φ_i зависит от вектора и поскольку последний сформирован на основе фактических измерений в ОЭП, ясно, что это и есть значение виртуального измерения зенитного расстояния звезды на фактической (истинной) орбите.

Поскольку и ТОСК, и ГЭИСК - ортогональные системы, то величина угла при переходе между ними сохраняется. Это означает, что, рассчитав таким образом угол, мы обходим вопрос о фактическом рассогласовании осей ТОСК опорной орбиты в сравнении с ТОСК истинной орбиты.

Последнее обстоятельство является основой утверждения о практической реализуемости алгоритма решения навигационной задачи по виртуальным измерениям. Иными словами, несмотря на то, что все решение навигационной задачи идет в ГЭИСК (как и предусматривает классический подход), расчет угла осуществляют в ТОСК.

В свою очередь, исключение из расчета угла φ_i перехода между ТОСК и ГЭИСК приводит к значительному повышению точности этого расчета и, в конечном итоге, к росту точности навигации.

Расчет местных градиентов угла φ_i осуществляют в ГЭИСК с использованием опорной орбиты. Поскольку в ГЭИСК , где - радиус-вектор орбиты, r=(х²+у²+z²)^1/2, то градиенты рассчитываются таким образом:

,

где - орт опорной орбиты в ГЭИСК, q - элемент массива параметров опорного положения КА в ГЭИСК, q={х,у,z}.

После расчета угла и его градиентов собственно навигационную задачу решают традиционно, используя выбранный сглаживающий фильтр. Например, при применении метода наименьших квадратов поправки к начальной точке опорной орбиты определяют итеративно по формуле:

где j - номер навигационного сеанса,

n - число навигационных сеансов на мерном интервале,

G_0j=G_j·Ф_0j - начальные градиенты, то есть производные от текущей измеряемой функции φ_ij по начальным параметрам опорной орбиты q₀,

- текущие (местные) градиенты,

i - число измерений в навигационном сеансе,

- весовая матрица измерений на j-м навигационном сеансе,

- матрица вторых моментов погрешностей измерений,

- баллистические (изохронные) производные,

q₀, q_j - соответственно начальные и текущие параметры опорной орбиты,

Δq_0c - поправка к начальным параметрам опорной орбиты на с-й итерации,

Δφ_ij=φ_ijизм-φ_ijрасч - невязка измерений.

Отметим, что в отличие от решения навигационной задачи в прототипе (по информации жестко закрепленных ОЭП), где матрицу и невязки измерений необходимо рассчитывать с учетом влияния углов отклонения корпуса КА относительно оси S:

, Δφ=ΔS+Δ_оэп,

где σ_S, ΔS - средняя квадратическая и систематическая погрешности расчета орта радиус-вектора орбиты, σ_оэп, Δ_оэп - аналогичные погрешности в ОЭП, здесь и Δφ_ij рассчитываются только на основе погрешности визирования σ_φ=σ_оэп, Δφ=Δ_оэп, поэтому решение навигационной задачи становится намного точнее.

Алгоритм решения задачи ориентации при одном жестко закрепленном ОЭП построен на использовании (5) так же, как это делается при оценке орбиты.

Действительно, если использовать измеренные координаты звезд ξ_i η_i (см. рис.1) не в каждом навигационном сеансе, а на всем мерном интервале совокупно и рассчитать чувствительность их по отношению к углам ориентации, то можно получить сглаженные по МНК итеративные оценки ориентации (алгоритм 3).

Из рис.1 следует, что в приборной системе координат ξ, η, ζ из подобия параллелепипедов, построенных на координатах орта звезды и координатах изображения этой звезды (ξ_i, η_i, ζ_i), можно определить, с одной стороны, значение измеренных координат:

и с другой, значения координат орта звезды:

где , ƒ - фокусное расстояние.

При жестком креплении ОЭП под углами α и δ относительно строительных осей КА (X_свY_свZ_св; Х_св - по продольной оси; Y_св - по боковой оси) орт звезды в связанной системе определится:

где МП1 - матрица перехода от приборной к связанной системе координат:

Здесь α - угол между проекцией оптической оси на плоскость X_свY_св и осью Х_св, δ - угол между оптической осью и плоскостью X_свY_св.

Решение задачи ориентации согласно (5) позволяет учитывать не только постоянную составляющую погрешности стабилизации, но и наличие определенной динамики.

Согласно (5) в этом случае , а Ф_0j представляется как производная по времени от функции изменения погрешностей системы стабилизации на мерном интервале.

В моделирующей программе опробованы несколько таких функций: постоянные значения, линейная, квадратичная и синусоидальная функции (при условии не выхода их значений за пределы 7⁰).

Местные градиенты

,

где k=1, 2, 3 - номера каналов,

q={ϑ,ψ,γ},

определяются на основе использования упрощенной матрицы (МП2)^T, матрицы (МП1)^T и (7). Применяя правило дифференцирования полученной сложной функции и решая систему двух линейных уравнений с двумя неизвестными, получим

для тангажа, k=1

для рыскания, k=2

для крена, k=3

,

,

где .

На основе представленных алгоритмов разработана имитационная модель системы, которая строилась с учетом всех сил, действующих на КА в полете. Рассчитывалась космическая обстановка (положение Луны, Солнца, планет), оценивалась возможность измерений, контролировалась работа алгоритмов распознавания и оптимизации выбора навигационных звезд, распознавалась "картинка" поля звезд, попавших в ОЭП, строился годограф положения оси ОЭП на небесной сфере.

Эти и другие элементы визуализации процесса решения, примененные в модели, позволяли осуществлять контроль над процессом, глубже понять его и убедиться в реализуемости идеи.

Были исследованы десять типов орбит, от низких (высота 200-300 км), до геостационара, от околокруговых до сильновытянутых (эксцентриситет порядка 0,7-0,8), от полярных (наклонение порядка 85°-86°) до экваториальных.

Отметим, что программа модели позволяет осуществлять решения при любом количестве ОЭП (до пяти) и решать при этом либо только навигационную задачу, либо обе задачи: навигации и ориентации.

Решения осуществлялись на один мерный интервал (1-2 оборота) и на ряд последовательных мерных интервалов (до 35). Решение на один мерный интервал, называлось однократным, оно базировалось на 50-1000 навигационных сеансах и оценивалось максимальным отклонением между навигационной оценкой (оценкой ориентации) и истинной орбитой (фактическим отклонением осей) по всему мерному интервалу (апостериорная гарантированная оценка). На последовательных интервалах оценивалась статистическая оценка точности на основе гарантированных оценок однократных решений. Определялись максимум максиморум, математическое ожидание и среднее квадратическое отклонение.

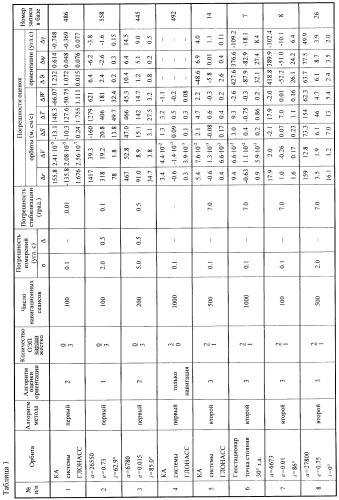
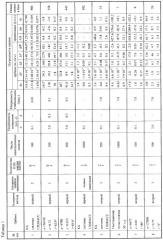
Статистические оценки заносились в базу данных решений. Каждая запись базы содержит результаты решений и исходные данные, позволяющие повторять решения. В табл.1 представлен ряд таких записей, где в графе «алгоритм метода» прототип обозначен как «первый».

Способ автономной навигации и ориентации космических аппаратов (КА), отличающийся различным креплением к корпусу КА оптико-электронных приборов (ОЭП), два из которых помещены в кардановы подвесы и визируют оптимально выбранные самые яркие звезды небесной сферы, один жестко крепится к корпусу; включающий для решения навигационной задачи компьютерный расчет виртуальных зенитных расстояний визируемых звезд на основе использования пространственного положения радиус-вектора опорной (априори полагаемой) орбиты без фактического построения местной вертикали, для решения задачи ориентации - распознавание компьютерным расчетом, с использованием звездного бортового каталога и опорной орбиты, звезд, попавших в поле зрения жестко закрепленного ОЭП, измерение приборных координат самой яркой звезды и расчет чувствительности измерений к углам ориентации; обе задачи решаются одновременно, и, благодаря различным способам крепления ОЭП, точность решения обеих задач существенно повышается по сравнению с точностью прототипа.