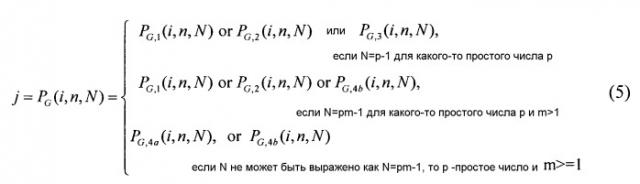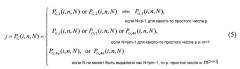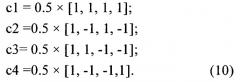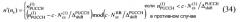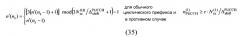Устройство и способ перераспределения ресурсов и перегруппировки в системе беспроводной связи

Устройство и способ перераспределения ресурсов и перегруппировки в системе беспроводной связи

Иллюстрации

Показать все

Реферат

УРОВЕНЬ ТЕХНИКИ

Область техники, к которой относится изобретение

Настоящее изобретение относится к способам и устройствам перераспределения и перегруппировки ресурсов для передачи в системе беспроводной связи.

Уровень техники

Средства связи позволяют осуществлять передачу данных на расстояние с целью осуществления связи между передатчиком и приемником. Данные обычно переносятся радиоволнами и передаются, используя ограниченные ресурсы передачи. То есть радиоволны передаются в течение некоторого периода времени, используя ограниченный частотный диапазон.

В системах по стандарту Long Term Evolution Проекта партнерства третьего (3-го) поколения (3GPP LTE) один из типов ресурса передачи, используемый в канале управления восходящей линии связи (PUCCH), известен как циклический сдвиг (CS) для каждого символа OFDM. Например, PUCCH занимает двенадцать поднесущих в одном ресурсном блоке (RB) и, следовательно, в одном RB имеются двенадцать ресурсов CS.

Кроме того, в соответствии с текущим рабочим допущением по передаче блока подтверждения для канала UL подтверждения (ACK) и опорного сигнала (RS), сигналы подтверждения и отсутствия подтверждения (ACK/NAK) и RS в восходящей линии связи (UL) для демодуляции ACK/NACK мультиплексируются по кодовым каналам, образованным как циклическим сдвигом (CS) базовой последовательности, так и ортогональным покрытием (OC). Одним из примеров базовой последовательности является последовательность Задова-Чу.

Одним из важных аспектов проекта системы является распределение ресурсов на уровне символов, интервалов или субкадров. Хотя в прошлом были предложены некоторые способы, такие как подход, основанный на таблице перераспределения, раскрытый в ссылке [5], подход, основанный на упомянутой таблице перераспределения, требует хранения таблицы перераспределения и поэтому нежелателен. В настоящем изобретении мы пытаемся найти эффективный, но все же общий способ перераспределения ресурсов.

РАСКРЫТИЕ ИЗОБРЕТЕНИЯ

Задача настоящего изобретения состоит в обеспечении улучшенных способов и устройства для беспроводной связи.

Другая задача настоящего изобретения заключается в обеспечении улучшенных способов и устройства для эффективного перераспределения и перегруппировки ресурсов передачи в системе беспроводной связи.

В соответствии с одним аспектом настоящего изобретения, глобальная схема распределения ресурсов организуется между N комбинациями ресурсов в первом временном интервале и N комбинациями ресурсов во втором временном интервале в зависимости от определенного параметра n. Схема распределения устанавливается следующим образом:

j=g(i,n),

где i означает индекс комбинации ресурсов в первом временном интервале и i=1,2,...N, j означает индекс комбинации ресурсов во втором временном интервале, и j=1,2,...,N, и g(a,b) является псевдослучайной функцией.

Псевдослучайная функция может быть функцией перестановок, основанной на поле Галуа, устанавливаемой следующим образом:

j=g(i,n)=P _G (i,n,N),

где n выбирается из набора целых чисел {l,2,...,N}. Альтернативно, псевдослучайная функция может быть усеченной битовой функцией обратного порядка (PBRO), описываемой следующим образом:

j=g(i,n)=PRBO(mod(i+n-l,N)+l,N).

Параметр n может быть одним и тем же для всех ячеек в сети связи.

Альтернативно, параметр n может быть назначен каждой ячейке в сети связи в зависимости от идентификации ячейки.

Каждая из комбинаций ресурсов содержит ортогональное покрытие, выбранное из множества ортогональных покрытий, и циклический сдвиг базовой последовательности, выбранный из множества циклических сдвигов. Схема скачкообразной перестройки циклического сдвига на уровне символов для конкретной ячейки может быть установлена для сдвига индекса циклического сдвига в пределах, по меньшей мере, одной комбинации ресурсов на символе модуляции в субкадре в ячейке на величину, указанную выражением h_sym(c_id,s_id,l_id). Индекс v _i ' циклического сдвига после сдвига, имевший индекс v до сдвига, в пределах i-й комбинации ресурсов описывается следующим образом:

v _i '=cyclic_shift(v _i ,h_sym(c_id, s_id, l_id), K),

где c_id означает идентификацию ячейки, s_id означает идентификацию субкадра, l_id означает идентификацию символа модуляции, K означает общее число многочисленных циклических сдвигов, и cyclic_shift(a,b,N)=mod(a+b-1,N)+l, когда множество циклических сдвигов индексируются как 1,2,...,N.

Функция h_sym(c_id,s_id,l_id) может быть одной из функций перестановок, основанной на поле Галуа, описываемой следующим образом:

h_sym(c_id,s_id,l_id)=P _G (x(l_id,K),r(c_id,n,K),K),

и усеченной битовой функцией обратного порядка (PBRO), описываемой следующим образом:

h_sym(c_id,s_id,l_id)=PBRO(mod(l_id+c_id+n-1,K)+1,K),

где x(l_id,K)=mod(l_id-1,K)+1 и r(c_id,n,K)=mod(c_id+n-l,K)+l.

Альтернативно, схема скачкообразной перестройки циклического сдвига на уровне символов для конкретной ячейки может быть установлена для сдвига индекса циклического сдвига в пределах по меньшей мере одной комбинации ресурсов во временном интервале в ячейке на величину, указанную выражением h_slot(c_id,sl_id). Индекс v _i ' циклического сдвига после сдвига, имеющего индекс v _i до сдвига, в пределах i-й комбинации ресурсов описывается следующим образом:

v _i '=cyclic_shift(v _i ,h_slot(c_id, sl_id),K),

где c_id означает идентификацию ячейки, sl_id означает идентификацию временного интервала, K означает общее количество многочисленных циклических сдвигов, и cyclic_shift(a,b,N)=mod(a+b-1,N)+1, когда многочисленные циклические сдвиги индексируются как 1,2,...,N. Функция h_slot(c_id,sl_id) может быть одной из функций перестановок, основанной на поле Галуа, описываемой следующим образом:

h_slot(c_id, sl_id)=P _G (sl_id,r(c_id,n,K),K),

и усеченной битовой функцией обратного порядка (PBRO), описываемой следующим образом:

h_slot(c_id,s_id,l_id)=PBRO(mod(sl_id+c_id+n-1,K)+1,K),

где r(c_id,n,K)=mod(c_id+n-l,K)+1.

В соответствии с другим аспектом настоящего изобретения, сначала N комбинаций ресурсов внутри каждого из множества временных интервалов делятся на K поднаборов, с k-м поднабором, содержащим N _k комбинаций ресурсов, где k=1,2,...,K. Схема распределения ресурсов внутри поднабора организуется между комбинациями ресурсов в поднаборах в первом временном интервале и комбинациями ресурсов в поднаборах во втором временном интервале в зависимости от определенного вектора параметров n=[n ₁ ,n ₂ ,...,n _k], где n _k соответствует k-му поднабору. Схема распределения описывается следующим образом:

i _k,d=g _k (i,n)=g _k(i _k,c ,n _k), для k=1, 2,...,K

где i=i _k,c, i _k,c означает индекс комбинации ресурсов внутри N комбинаций ресурсов в первом временном интервале, k означает индекс поднабора, в котором расположена i _k,c-ая комбинация ресурсов, c означает индекс i _k,c-й комбинации ресурсов внутри k-го поднабора, i _k,d означает индекс комбинации ресурсов внутри N комбинаций ресурсов во втором временном интервале, k означает индекс поднабора, в котором располагается i _k,d-ая комбинация ресурсов, d означает индекс i _k,d-й комбинации ресурсов внутри k-го поднабора, i _k,c=(k-l)xN _k+c, i _k,d=(k-1)xN _k+d, и g(a,b) является псевдослучайной функцией.

В соответствии с еще одним другим аспектом настоящего изобретения, первые N комбинаций ресурсов внутри каждого из множества временных интервалов делятся на K поднаборов с k-м поднабором, содержащим N _k комбинаций ресурсов, где k=1,2,..., K, и N ₁=N ₂=...=N_k. Схема перемежения между поднаборами организуется, по меньшей мере, в одном временном интервале в соответствии с параметром перемежения PG[s ₁,s ₂,...,s _k]. Схема перемежения между поднаборами организуется следующим образом:

j=w(i,PG[s ₁,s ₂,...,s _k]), для k=l,2,...,K,

где w(i,PG[s ₁,s ₂,...,s _k]) означает i-ую комбинацию ресурсов во временном интервале после перемежения в соответствии с параметром перемежения PG[s ₁,s ₂,...,s _k]) и параметр перемежения PG[s ₁, s ₂,..., s _k]) указывает, что поднабор, имеющий индекс s _k до перемежения, имеет индекс k после перемежения, и l≤s ₁,...,s _k≤K.

В соответствии с еще одним другим аспектом настоящего изобретения, схема распределения с циклическими сдвигами на уровне символов организуется между M циклических сдвигов в первом символе модуляции в канале передачи и M циклических сдвигов во втором символе модуляции в канале передачи в зависимости от определенного параметра n. Первый символ модуляции имеет идентификационный номер 1, а второй символ модуляции имеет идентификационный номер больше 1. Схема распределения с циклическими сдвигами на уровне символов описывается следующим образом:

m'=t(m,l_id, n), для l_id>1,

где m означает индекс циклического сдвига внутри первого символа модуляции и m=1,2,...,M, m' означает индекс циклического сдвига внутри второго символа модуляции и m'=l,2,...,M, l_id означает идентификационный номер второго символа модуляции, и t(a,b,c) является псевдослучайной функцией.

В соответствии с еще одним другим аспектом настоящего изобретения, схема распределения с циклическими сдвигами на уровне интервалов организуется между M циклических сдвигов в первом временном интервале в канале передачи и M циклических сдвигов во втором временном интервале в канале передачи в зависимости от определенного параметра n. Схема распределения с циклическими сдвигами на уровне интервалов описывается следующим образом:

m'=g(m,n),

где m означает индекс циклического сдвига внутри первого временного интервала и m=1,2,...,M, m' означает индекс циклического сдвига внутри второго временного интервала и m'=1,2,...,M, и g(a,b) является псевдослучайной функцией.

В соответствии с дополнительным аспектом настоящего изобретения, схема распределения базовых последовательностей на уровне субкадров организуется между Z базовых последовательностей в первом субкадре в канале передачи и Z базовых последовательностей во втором субкадре в канале передачи в зависимости от определенного параметра n. Первый субкадр имеет идентификационный номер 1, а второй субкадр имеет идентификационный номер больше 1. Схема распределения базовых последовательностей на уровне субкадров описывается следующим образом:

z'=s(z,s_id,n), для s_id>1,

где z означает индекс базовой последовательности внутри первого субкадра и z=1,2,...,Z, z' означает индекс базовой последовательности внутри второго субкадра и z'=l,2,...,Z, s_id означает идентификационный номер второго субкадра, и s(a,b,c) является псевдослучайной функцией.

В соответствии с еще одним аспектом настоящего изобретения, схема распределения базовых последовательностей на уровне интервалов организуется между Z базовых последовательностей в первом временном интервале и Z базовых последовательностей во втором временном интервале 1 в зависимости от определенного параметра n. Первый временной интервал имеет идентификационный номер 1, а второй временной интервал имеет идентификационный номер больше 1. Схема распределения базовых последовательностей сдвигов на уровне интервалов описывается следующим образом:

z'=s(z,sl_id,n), для sl_id>1,

где z означает индекс базовой последовательности внутри первого временного интервала и z=1,2,...,Z, z' означает индекс базовой последовательности внутри второго временного интервала и z'=l,2,...,Z, sl_id означает идентификационный номер второго временного интервала, и s(a,b,c) является псевдослучайной функцией.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Более полное понимание изобретения и многие присущие ему преимущества станут легко видны, а также будут более понятны при обращении к последующему подробному описанию при рассмотрении его в сочетании с сопровождающими чертежами, на которых одинаковые ссылочные позиции указывают на одни и те же или аналогичные компоненты, на которых:

фиг.1 - схема цепочки приемопередатчика системы мультиплексирования с ортогональным частотным разделением каналов (OFDM), пригодного для практического осуществления принципов настоящего изобретения;

фиг.2 - схематический пример мультиплексирования шести блоков оборудования пользователя (UE) внутри одного блока ресурсов (RB); и

фиг.3 - схематический показ текущего рабочего допущения для каналов подтверждения и опорного сигнала восходящей линии связи.

ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ

В настоящее изобретение путем ссылки включены следующие материалы:

[1] 3GPP RANl#50 Chairman's Notes, August 2007, Athens, Greece

[2] 3GPP RANl#50 Chairman's Notes, August 2007, Athens, Greece

[3] 3GPP RANl#50 Chairman's Notes, August 2007, Athens, Greece

[4] Rl-072225, "CCE to RE mapping", Samsung, RANl #49, Kobe, May 2007

[5] Rl-073412, "Randomization of intra-cell interference in PUCCH", ETRI, RANl#50, Athens, August 2007

[6] Rl-073413, "Sequence allocation and hopping for uplink ACK/NACK channels", ETRI, RANl#50, Athens, August 2007

[7] Rl-073661, "Signaling of implicit ACK/NACK resources", Nokia Siemens, Nokia, RANl#50, Athens, August 2007

[8] Rl-080983, "Way forward on the Cyclic Shift Hopping for PUCCH", Panasonic, Samsung, ETRI, RAN1#52, Sorrento, Italy, February, 2008

[9] 3GPP TS 36.211, version 8.3.0, May, 2008

На фиг.1 показана цепочка приемопередатчика системы мультиплексирования с ортогональным частотным разделением каналов (OFDM). В системе связи, использующей технологию OFDM, в цепочке 110 передатчика сигналы управления или данные 111 модулируются модулятором 112 в последовательность символов модуляции, которые последовательно преобразуются из последовательной формы в параллельную последовательно-параллельным (S/P) преобразователем 113. Блок 114 обратного быстрого преобразования Фурье (IFFT) используется для преобразования сигналов из частотной области во временную область во множество сигналов OFDM. Циклический префикс (CP) или нулевой префикс (ZP) добавляется к каждому символу OFDM блоком 116 вставки на CP, чтобы избежать или смягчить влияние многолучевого замирания. В результате сигнал передается внешним блоком 117 обработки передатчика (Тх), таким как антенна (не показана), или, альтернативно, с помощью стационарной проводной или кабельной сети. В приемной цепочке 120, полагая, что временная и частотная синхронизация полностью достигнута, сигнал, принятый внешним блоком 121 обработки приемника (Rx), обрабатывается блоком 122 удаления СР. Блок 124 быстрого преобразования Фурье (FFT) преобразует принятый сигнал из временной области в частотную область для дальнейшей обработки.

Общая ширина полосы пропускания системы OFDM делится на узкополосные частотные интервалы, называемые поднесущими. Количество поднесущих равно используемому в системе размеру N FFT/IFFT. В целом, количество поднесущих, используемых для данных, меньше, чем N, поскольку некоторые поднесущие на краю частотного спектра резервируются как защитные поднесущие. В целом, на защитных поднесущих никакая информация не передается.

На восходящих линиях связи (UL) по стандарту Long Term Evolution Проекта партнерства третьего (3-го) поколения (3GPP LTE) один из типов ресурса передачи, используемый в канале управления восходящей линии связи (PUCCH), известен как циклический сдвиг (CS) для каждого символа OFDM. Например, PUCCH занимает двенадцать поднесущих в одном блоке ресурсов (RB) и, следовательно, двенадцать ресурсов CS в одном RB. Пример мультиплексирования шести блоков оборудования пользователя (UE) в одном RB показан на фиг.2. Отметим, что в этом примере используются только шесть из двенадцати CS.

На фиг.3 показано текущее рабочее допущение для блока передачи каналов подтверждения (ACK) и опорного сигнала (RB). Сигналы ACK/NAK и UL RS для демодуляции ACK/NACK мультиплексируются на кодовых каналах, образуемых циклическим сдвигом (CS) базовой последовательности и ортогональным покрытием (OC). Одним из примеров базовой последовательности является последовательность Задова-Чу.

Одним из важных аспектов проекта системы является распределение ресурсов на уровне символов, интервалов или субкадров. Хотя в прошлом были предложены некоторые способы, такие как таблица перераспределения, основанная на подходе, раскрытом в ссылке [5], таблица перераспределения, основанная на упомянутом подходе, требует хранения таблицы перераспределения и поэтому нежелательна. В настоящем изобретении мы пытаемся найти эффективный, но все еще общий способ перераспределения ресурсов.

В настоящем изобретении мы впервые предлагаем набор новых алгоритмов перестановок, а также предлагаем применить эти алгоритмы и известный усеченный битовый алгоритм обратного порядка (PBRO) к нескольким различным проблемам перераспределения/перегруппировки, в том числе к перераспределению с циклическими сдвигами (CS)/ортогональным покрытием (OC) на уровне интервалов или символов, к созданию схем скачкообразной перестройки с помощью CS на уровне интервалов и символов для конкретных ячеек и к созданию схем скачкообразной перестройки базовых последовательностей на уровне субкадров и интервалов.

Кроме того, мы отмечаем, что усеченный битовый алгоритм обратного порядка (PBRO или иногда известный как алгоритм "PBRI", где "I" вставляется для перемежения) является известным способом и использовался во многих применениях, например, распределение элемента канала управления (CCE) в элементах ресурсов (RE), раскрытое в ссылке [4]. Способ PBRO создает перестановку y=PBRO(i, M) последовательности {1,2,..., M} размера M, где y является выходным значением, соответствующим входному значению i. PBRO устанавливается следующим образом:

Пусть i=i-1, так что i принадлежит к последовательности {0,1,...,M-1}. Определим параметр n PBRO, где n - наименьшее целое число, такое как M≤2ⁿ.

Установим счетчики i и j в исходное положение на 0.

Определим x как значение j с обратным порядком битов, используя n-битовое двоичное представление. Например, если n=4 и j=3, то x=12.

Если х<M, установим PBRO(i,M) на х и увеличим i на 1.

Дадим приращение счетчику j.

Если i<M переходим к этапу 3. В противном случае переходим к этапу 7.

Пусть j=j+1, так что j принадлежит к набору {0,1,...,M}.

Аспекты, признаки и преимущества изобретения явно видны из последующего подробного описания, просто путем показа нескольких конкретных вариантов осуществления, в том числе предпочтительного варианта, подразумеваемого для выполнения изобретения. Изобретение также пригодно для других или отличных вариантов осуществления и некоторые его подробности могут изменяться в различных очевидных отношениях, причем без какого-либо отступления от сущности и объема изобретения. Соответственно, чертежи и описание должны рассматриваться по своему характеру как примеры, но не как ограничения. Изобретение демонстрируется на примерах и не в качестве ограничения, на фигурах сопроводительных чертежей.

1. Предложенный алгоритм перестановок

В первом варианте осуществления, в соответствии с принципами настоящего изобретения, мы предлагаем функцию перестановки ресурсов, которая основывается на операциях поля Галуа. Пусть N является общим количеством переставляемых ресурсов, тогда операции функции перестановок описывается следующим образом:

j=P _G(i,n,N) (1)

где i=l,...,N является индексом входных ресурсов, j=l, ...,N является индексом выходных ресурсов, и n=l,...,N является индексом последовательности перестановок, поскольку другое значение n обеспечивает выход с другими перестановками.

Сначала мы рассматриваем случай, где N является целым числом, удовлетворяющим условию N=p ^m-1, где p является простым числом и m является положительным целым числом. В этом случае поле Галуа N+1 существует и мы отмечаем его как GF(N+1). Кроме того, мы можем найти примитивный элемент этого поля Галуа и назвать примитивный элемент α, который удовлетворяет условию α^N=α^pm-1=1, и α является целым числом. Кроме того, все N ненулевых элементов в GF(N+1) могут быть выражены как экспонент α или, другими словами, последовательность α⁰,α^l,...,α^N-1 содержит все N ненулевых элементов в GF(N+1). Следовательно, любой номер i входного ресурса может быть выражен как показатель степени примитивного элемента i=α^k для любого целого числа k, такого, что 0≤k≤N-1. С учетом этого замечания выход функции перестановки ресурсов P _G(i,n,N) описывается следующим образом:

j=P _G,1(i,n,N)=α^mod(k+n-1,N) для i=1,...,N, и n=l, ...,N, (2)

где mod(a,b) является операцией по модулю, применяемой к двум целым числам a и b. Другая подобная функция перестановок может быть найдена как:

j=P _G,2(i,n,N)=α^{mod(k-(n-1),N)} для i=1,...,N, и n=l, ...,N (3)

Заметим, что мы можем обратиться за помощью к вычислению окончательного поля, чтобы найти представление натурального числа j в приведенном выше уравнении.

С другой стороны, мы рассмотрим особый случай, где N является целым числом, удовлетворяющим условию N=p ^j-1, где p является простым числом. В этом случае, поле Галуа N+l, то есть GF(N+1), также существует и также является основным полем Галуа. В этом случае, мы предлагаем более простой подход к нахождению выходного перестановленного ресурса:

j=P _G,3(i,n,N)=mod(ixn,N+1) для i=1,...,N, и n=l, ...,N (4)

Дополнительно, если N не удовлетворяет условию N=p ^m-1, для некоторого простого числа p и положительного целого числа m, то мы предлагаем следующий подход на основе усеченного поля GF, который мы обозначаем как P _G,4α(i,n,N):

Этап 1: Найти наименьшее целое число M>N, такое что М удовлетворяет условию M=p ^m-1, где p - простое число и m - положительное целое число. Сформировать поле Галуа GF(M+1), найти примитивный элемент α для GF(M+1). Установить переменные u=l и v=l.

Этап 2: Найти w следующим способом: если M=p ^m-1, где p простое число и m>1, то w может быть создано либо как w=P _G,1(v,n,M), либо как w=P _G,2(v,n,M); если M=р-1, где р - простое число, то тогда w может быть создано с помощью одной из трех функций, перечисленных выше: w=P _G,1(v,n,M), w=P _G,2(v,n,M) и w=P _G,3(v,n,M).

Этап 3: если w>N, пусть v=v+1, перейти к этапу 2; в противном случае перейти к этапу 4.

Этап 4: если u=i, перейти к этапу 5; в противном случае, пусть u=u+1, v=v+1 и перейти к этапу 2.

Этап 5: Мы получили индекс выходного ресурса j=w=P _G,4α(i,n,N).

Мы также предложили подобный способ для случая, когда N не удовлетворяет условию N=p-1, для некоторого простого числа p, затем мы предложили следующий подход на основе основного усеченного поля GF, которое мы означаем через P _G,4b(i,n,N):

Этап 1: Найти наименьшее M>N, такое что М удовлетворяет условию M=p-1, где p - простое число. Установить переменные u=l и v=l.

Этап 2: Найти w как w=P _G,3(v,n,M).

Этап 3: если w>N, пусть v=v+1, перейти к этапу 2; в противном случае, перейти к этапу 4.

Этап 4: если u=i, перейти к этапу 5; в противном случае, пусть u=u+1, v=v+1 и перейти к этапу 2.

Этап 5: Мы получили индекс выходного ресурса j=w=P _G,4b(i,n,N).

Теперь обобщим предложенную функцию перестановок. Следовательно, для набора входных значений i,n,N, где l≤i≤N и l≤n≤N, результат перестановок описывается следующей функцией:

Примечательно то, что в описанных выше способах мы предполагали входные и выходные ресурсы индексированными как i=1,...,N, и j=l,...,N. Если входной индекс i' и выходной индекс j' индексированы как i'=0,...,N-1 и j'=0,...,N-l, то приведенное выше уравнение должно использоваться следующим образом:

j'=P _G(i'+1,n,N)-1; для i'=0,...,N-1, j'=0,...,N-1, и n=1,...,N (6)

2. Перераспределение ресурсов на уровне интервалов для комбинаций с ортогональным покрытием/циклическим сдвигом

Сначала рассмотрим случай, когда в каждом из двух интервалов канала управления восходящей линии связи доступны в общей сложности N ресурсов и каждый ресурс определяется как комбинация с ортогональным покрытием и циклическим сдвигом (объединенный ресурс OC/CS). Примером применения этого типа назначения объединенного ресурса является канал ACK/NACK восходящей линии связи. Заметим, что канал запроса предоставления обслуживания по восходящей линии связи может повторно использовать структуру канала ACK/NACK восходящей линии связи. Другим примером применения этого типа назначения объединенного ресурса является канал опорных символов демодуляции восходящей линии связи.

Одним из примеров ортогонального покрытия является код Уолша-Адамара.

С другой стороны, циклический сдвиг (CS) обычно применяется к базовой последовательности, к примерам базовой последовательности относятся код ZC (Задов-Чу) и компьютерно-генерируемые коды CAZAC (Constant Amplitude Zero Auto-Correlation (нулевой автокорреляции с постоянной амплитудой)). Для любой базовой последовательности длиной N существуют N циклических сдвигов или N ресурсов CS.

Обозначим здесь и далее объединенные ресурсы OC/CS как СВ. N объединенных ресурсов представляются следующим образом:

CB _a[i]={OC _a[u _i],CS _a[v _i]}, для i=l,...,N, и a=1, 2, (7)

где u _i и v _i указывают индексы OC и CS для i-го объединенного ресурса, соответственно. Кроме того, a=1,2 является индексом интервалов внутри субкадра для передач по восходящей линии связи согласно стандарту 3GPP LTE.

2.1. Глобальное перераспределение ресурсов

Во втором варианте осуществления, соответствующем принципам настоящего изобретения, пусть имеется N объединенных ресурсов OC/CS в обоих интервалах субкадра восходящей линии связи. Мы предлагаем связать объединенные ресурсы OC/CS таким образом, что если UE выбирает объединенный ресурс CB ₁[i] в первом интервале, то UE должно быть назначено CB ₂[g(i,n)] во втором интервале, где g(i,n) является псевдослучайной функцией перераспределения/перестановки ресурсов и n является параметром.

В первом подварианте осуществления второго варианта осуществления, соответствующего принципам настоящего изобретения, псевдослучайная функция перестановок описывается следующим образом:

g(i,n)=P _G(i,n,N)(8)

где n выбирается из набора {1,2,...,N} или n=l,...,N. Функция P_G(i,n,N) определяется в предыдущем разделе.

Во втором подварианте осуществления второго варианта осуществления, соответствующего принципам настоящего изобретения, псевдослучайная функция перестановок использует функцию PBRO следующим образом:

g(i,n)=PBRO(mod(i+n-1,N)+l,N)(9)

Функция PBRO(a,b) определяется заранее и n выбирается из набора {1, 2, ..., N}.

В третьем подварианте осуществления второго варианта осуществления, соответствующего принципам настоящего изобретения, параметр n в приведенных двух подвариантах осуществления является одним и тем же для всех ячеек. Параметр n может быть сообщен UE посредством сигнализации более высокого уровня.

В четвертом подварианте осуществления второго варианта осуществления, соответствующем принципам настоящего изобретения, параметр n является функцией идентификатора ячейки, CELL ID (c_id), обозначенной как n=f(c_id). Следовательно, для другого c_id мы будем иметь другой параметр n. Одним из примеров такой функции является n=mod(c_id-1,N)+1.

Прежде чем показать пример таких описанных выше вариантов осуществленеия, представим таблицу для четырех поднаборов OC S ₁, S ₂, S ₃ и S ₄, как она представлена в ссылке [3]. Три кода в каждом поднаборе означены как S _i(A), S _i(B) и S _i(C).

Таблица 1Эквивалентное распределение между всеми наборамитрех ОС
Четыре поднабора	А	В	С
S 1	c2	c3	c1
S 2	c1	c4	c2
S 3	c4	c1	c3
S 4	c3	c2	c4

где набор кодов ОС представляется кодами Уолша в соответствии со ссылкой [3]:

Теперь мы переходим к примеру применения вариантов осуществления. Сначала распределение/определение объединенных ресурсов OC/CS приводится в таблице 2 для N=18, как представлено в ссылке [3].

Таблица 2Комбинации ресурсов OC/CS, определенные в двух интервалах, N=18
	Объединенные ресурсы в интервале №1 - СВ 1[ ]	Объединенные ресурсы в интервале №2 - СВ 2[ ]
Значение циклического сдвига	OC 1[1]	OC 1[2]	OC 1[3]	OC 2[1]	OC 2[2]	OC 2[3]
0	СВ 1[1]		[13]	СВ 2[1]		[13]
1		[7]			[7]
2	[2]		[14]	[2]		[14]
3		[8]			[8]
4	[3]		[15]	[3]		[15]
5		[9]			[9]
6	[4]		[16]	[4]		[16]
7		[10]			[10]
8	[5]		[17]	[5]		[17]
9		[11]			[11]
10	[6]		[18]	[6]		[18]
11		[12]			[12]

Заметим здесь, что OC ₁[1], OC ₁[2], OC ₁[3] являются тремя кодами OC, используемыми в интервале 1, а OC ₂[1], OC ₂[2], OC ₂[3] являются тремя кодами OC, используемыми в интервале 2. В целом, коды OC в каждом интервале могут быть произвольным поднабором из четырех длиной-4 кодов Уолша {cl, c2, c3, c4}, определенных в таблице 1. Один из примеров выбора кодов OC состоит в том, что коды OC в первом интервале задаются как OC ₁[1]=S _i(A), OC ₁[2]=S _i(C), OC ₁[3]=S _i(B) и коды OC во втором интервале задаются как OC ₂[1]=S _j(A), OC ₂[2]=S _j(C), OC ₂[3]=S _j(B) для пары целых чисел (i,j) (ссылка [3]). Например, если i=j=2, то мы имеем OC ₁[1]=OC ₂[1]=S ₂(A)=c1, OC ₁[2]=OC ₂[2]=S ₂(C)=c2 и OC ₁[3]=OC ₂[3]=S ₂(B)=c4.

Теперь найдем в этом примере из 18 объединенных ресурсов OC/CS, приведенных в таблице 2, связь/перераспределение между объединенными ресурсами в интервале 1 и интервале 2. Заметим, что та же самая связь/перераспределение применяется в любом другом случае, где присутствуют N=18 комбинаций OC/CS, таком как альтернативная схема распределения, показанная в таблице 19 в Приложении. Поскольку N=18 и N+1=19 является простым числом и GF(19) является основным полем Галуа, мы можем использовать g(i,n)=P _G,3(i,n,18)=mod(ixn,19) как функцию перестановок g(i,n), которая связывает ресурс CB ₁[i] интервала 1 и ресурс CB ₂[g(i,n)] интервала 2. Эта функция перераспределения ресурсов показана ниже в таблице 3. Заметим, что показаны только n=l - n=4, другие значения параметров n=5 - n=18 также могут использоваться при создании функции g(i,n).

Таблица 3Функция g(i,n) перестановки/перераспределения ресурсов как функция параметра n. N=18
i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
g(i,n),n=1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
g(i,n),n=2	2	4	6	8	10	12	14	16	18	1	3	5	7	9	11	13	15	17
g(i,n),n=3	3	6	9	12	15	18	2	5	8	11	14	17	1	4	7	10	13	16
g(i,n),n=4	4	8	12	16	1	5	9	13	17	2	6	10	14	18	3	7	11	15

В другом примере мы имеем N=12 или 12 объединенных ресурсов OC/CS в каждом интервале, как показано в приведенной ниже таблице 4.

Таблица 4Комбинации ресурсов OC/CS, определенные в двух интервалах, представленные в ссылке [3]. N=12
	Объединенные ресурсы в интервале №1 - СВ 1[ ]	Объединенные ресурсы в интервале №2 - СВ 2[ ]
Значение цикличес-кого сдвига	OC 1[1]	OC 1[2]	OC 1[3]	OC 2[1]	OC 2[2]	OC 2[3]
0	СВ 1[1]			СВ 2[1]
1		[5]			[5]
2			[9]			[9]
3	[2]			[2]
4		[6]			[6]
5			[10]			[10]
6	[3]			[3]
7		[7]			[7]
8			[11]			[11]
9	[4]			[4]
10		[8]			[8]
11			[12]			[12]

Теперь найдем связь между объединенными ресурсами в интервале 1 и интервале 2 в этом примере, приведенном в таблице 4. Заметим, что эта же самая связь/перераспределение может применяться в любом другом случае, где существуют N=12 комбинаций OC/CS. Поскольку N=12 и N+l=13 является простым числом и GF(13) является основным полем Галуа, мы можем использовать g(i,n)=P _G,3(i,n,12)=mod(i×n,13) как функцию перестановок g(i,n), которая связывает ресурс CB ₁[i] интервала 1 и ресурс CB ₂[g(i,n)] интервала 2.

Эта функция перераспределения ресурсов показана ниже в таблице 5. Заметим, что показаны только n=l - n=3, другие значения параметров n=5 - n=12 также могут использоваться при создании функции g(i,n).

Таблица 5Функция g(i,n) перестановки/перераспределения ресурсов как функция параметра n. N=12
i	1	2	3	4	5	6	7	8	9	10	11	12
g(i,n),n=1	1	2	3	4	5	6	7	8	9	10	11	12
g(i,n),n=2	2	4	6	8	10	12	1	3	5	7	9	11
g(i,n),n=3	3	6	9	12	2	5	8	11	1	4	7	10

В третьем варианте осуществления в соответствии с принципами настоящего изобретения, мы предлагаем назначить поднабор S _i и S _j интервалу 1 и 2 в субкадре для всех UE внутри заданной ячейки. Кроме того, мы предлагаем связать индексы поднаборов i и j с CELL ID, обозначенным как c_id. Один из примеров такой связи:

i=mod(c_id-1,4)+1, и j=mod(i