Способ некогерентного накопления светолокационных сигналов

Способ некогерентного накопления светолокационных сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к лазерной технике, а именно к лазерной дальнометрии.

Известны способы лазерного зондирования удаленных объектов для получения информации об их дальности и других характеристиках. Известен способ определения дальности до цели, включающий посылку на цель лазерного импульса S₀(t,t₀), регистрацию момента посылки t₀, прием отраженного целью излучения S(t,t_D), регистрацию момента приема t_D и определение временного интервала τ=t_D-t₀, по которому судят о дальности D до цели [1] по формуле D=сτ/2, где с - скорость света. Недостатком этого способа является необходимость применения мощных излучателей и высокочувствительных приемников для обеспечения широкого диапазона измерений дальности.

Энергетический потенциал измерителя дальности может быть увеличен за счет многократного повторения измерений (накопления), в частности методом некогерентного накопления. При таком способе характеристики обнаружения (вероятности ошибочного измерения или пропуска сигнала) могут быть улучшены за счет статистической обработки результатов многократного зондирования по их совокупности [2].

Наиболее близким по технической сущности к предлагаемому способу является способ некогерентного накопления светолокационных сигналов, включающий серию из N циклов зондирования, в каждом цикле зондирования производят посылку зондирующего светового импульса S₀(t,t₀), где t - текущее время, t₀ - момент излучения зондирующего импульса, квантуют время на отдельные дискреты длительностью Т, образуя тем самым ячейки дальности, в каждой из дискрет времени осуществляют прием отраженного сигнала S(t, t_D), где t_D - момент приема отраженного импульса, определяют его значение S_jm, накапливают значения S_jm в каждой j-й ячейке дальности путем формирования их сумм и по массиву сумм {S_j} судят о задержке τ принятого сигнала относительно зондирующего импульса τ=t_R-t₀, по которой определяют дальность до цели D=сτ/2, где с - скорость света, j=1, 2,… J - порядковый номер ячейки дальности, начиная от момента t₀, J - количество ячеек дальности; m=1, 2,… N - порядковый номер зондирования [3].

При большой максимальной дальности до цели, то есть при слабом отраженном целью сигнале, этот способ требует значительного объема накопления N и, соответственно, большого времени измерения. Этот может быть нежелательным и даже недопустимым при высоких требованиях к оперативности проведения измерений, например, если цель движется или доступна для наблюдения на короткое время.

Задачей изобретения является повышение оперативности измерения дальности при максимальной дальности действия и минимальных энергетических затратах.

Указанная задача решается за счет того, что в известном способе некогерентного накопления светолокационных сигналов, включающем серию из N циклов зондирования, в каждом цикле зондирования производят посылку зондирующего светового импульса S₀(t,t₀), где t - текущее время, t₀ - момент излучения зондирующего импульса, квантуют время на отдельные дискреты длительностью Т, образуя тем самым ячейки дальности, в каждой из дискрет времени осуществляют прием отраженного сигнала S(t, t_D), где t_D - момент приема отраженного импульса, определяют его значение S_jm, накапливают значения S_jm в каждой j-й ячейке дальности путем формирования их сумм , и по массиву сумм {S_j} судят о задержке τ принятого сигнала относительно зондирующего импульса τ=t_R-t₀, по которой определяют дальность до цели R=сτ/2, где с - скорость света, j=1, 2,… J - порядковый номер ячейки дальности, начиная от момента t₀, J - количество ячеек дальности, m=1, 2,… N - порядковый номер зондирования, устанавливают длительность t_и зондирующего импульса в пределах от 2Т до ΔT_D, где ΔТ_D - заданная разрешающая способность по дальности, предварительно производят оцифровку зондирующего импульса путем определения его выборочных значений S_0j с периодом выборок, равным тактовому периоду Т, где j=1, 2,… К - порядковый номер выборки начиная от момента t₀, К=t_и/T - количество выборок, и регистрации массива {S_0j} этих выборочных значений, а по завершении накопления пошагово сдвигают массив {S_j} относительно {S_0j}, на каждом шаге р=1, 2,… Р_mах проверяя степень их совпадения по заранее установленному критерию, например, по коэффициенту корреляции , где Р_mах - максимальное число шагов, соответствующее диапазону измерения дальности, определяют порядковый номер шага Р, на котором степень совпадения массивов {S_j} и {S_0j} оптимально соответствует принятому критерию, и определяют дальность D до цели по формуле D=сРТ/2, причем в процессе накопления определяют оценки среднеквадратического отклонения σs выборочных значений S_jm и их среднего значения M_s, устанавливают порог накопления C_N=Qσ_S+M_S, где Q - коэффициент превышения порога над шумом, определяемый из условия обеспечения максимальной вероятности правильного обнаружения в каждой ячейке дальности при заданной вероятности ложной тревоги во всем диапазоне измеряемых дальностей, и прекращают процесс накопления при количестве зондирований N, когда хотя бы в одной из ячеек дальности накопленная сумма S_j превысит пороговую величину C_N.

Для оценки среднеквадратического отклонения σ_S выборочных значений S_jm и их среднего значения M_S можно в одном из массивов {S_jm}, например, в массиве {S_j1} выделить группу статистически независимых выборочных значений в количестве М, и затем определить оценки среднего значения M_S и среднеквадратического отклонения σ_S по формулам ; , причем количество выборочных значений в этой группе предварительно устанавливают из условия обеспечения заданной точности оценок, например, с помощью уравнения

где

q - допустимая погрешность оценки;

γ - надежность оценки;

- плотность распределения случайной величины %;

;

- оценка величины обусловленного шумом среднеквадратического разброса выборок в массиве {S_j};

σ>0 - непрерывный параметр, имеющий размерность σ_S.

Вероятность правильного обнаружения сигнала во всем диапазоне измеряемых дальностей может быть увеличена, если в начале измеряемого интервала дальностей коэффициент Q устанавливают с превышением относительно среднего значения, а по мере увеличения порядкового номера j уменьшают его таким образом, чтобы вероятность ложной тревоги во всем измеряемом диапазоне дальностей не превышала заданного предела, причем начальное превышение коэффициента Q и его значения, соответствующие текущей дальности, задают из условия соблюдения требуемой вероятности обнаружения сигнала в каждой из ячеек дальности.

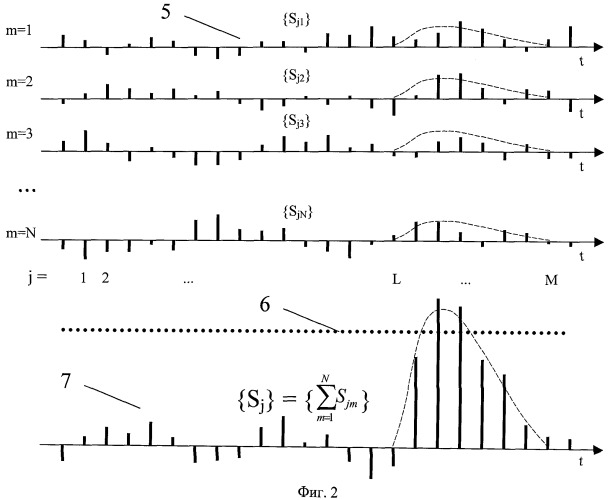
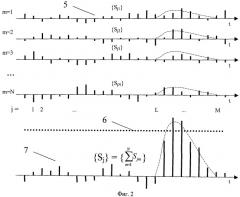
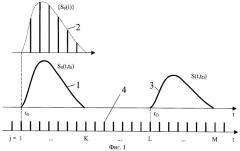
На Фиг.1 представлена временная диаграмма процесса зондирования и его привязка к тактовой частоте. Фиг.2 иллюстрирует формирование массива {S_j} путем накопления массивов {S_jm}. На Фиг.3 показано формирование функции корреляции R(p) массивов {S_j} и {S_0j}.

В момент времени t₀ в направлении цели посылают зондирующий импульс S₀(t,t₀) 1, соответствующий своим выборочным значениям, хранящимся в массиве {S_0j} 2, и затем принимают отраженный целью импульс S(t,t_D) 3. Момент излучения зондирующего импульса 1 привязан к тактовой последовательности 4 путем присвоения импульсу тактовой последовательности, совпадающему с моментом t₀, порядкового номера j=1. Тактовые импульсы генерируют с помощью высокостабильного источника с частотой F_T=1/Т, где Т - период следования тактовых импульсов. Массив 2 получают предварительно путем пробной посылки зондирующего импульса и его оцифровки с тактовой частотой F_T. Массив 2 сохраняют в памяти системы и обновляют его в процессе подготовки к измерениям каждый раз, когда это требуется по условиям метрологической калибровки. При каждом m-м зондировании принятый сигнал 3 оцифровывают путем определения его выборочных значений S_jm в моменты генерации каждого j-го тактового импульса; нумерация отсчетов S_jm ведется от тактового импульса с номером j=1. Полученные выборочные значения регистрируют в массивах {S_jm}, хранящихся в памяти системы (Фиг.2). По выборочным значениям S_j1 массива {S_j1} определяют статистические характеристики принимаемой смеси сигнала с шумом. Для этого выделяют часть массива {S_j1}, ограниченную номерами ячеек дальности J₁ и J₂, и определяют оценки среднего значения M_S и среднеквадратического отклонения σ_S1 по формулам ; , где J₁ и J₂ - границы части массива, выделенной для определения M_S и σ_S1, а затем определяют величину среднеквадратического разброса , причем количество выборочных значений в этой группе М=(J₂-J₁+1) предварительно устанавливают из условия обеспечения заданных доверительных интервалов разброса этих оценок. Например, если задана допустимая погрешность определения доверительного интервала q с надежностью оценки γ, то по известной методике [4, стр.221] можно определить необходимое для этого количество выборок М. Для этого необходимо решить уравнение

где

γ - надежность оценки;

- плотность распределения случайной величины %;

;

- оценка величины обусловленного шумом среднеквадратического разброса выборок в массиве {S_j};

σ - непрерывный параметр, имеющий размерность σ_S.

На практике для определения М предварительно задаются погрешностью q и надежностью оценки γ, после чего определяют М по заранее вычисленным зависимостям, например, по [4, стр.464, Приложение 4]. Так, при допустимой двадцатипроцентной ошибке (q=0,2) и надежности γ=0,95 величина массива выборки М=50. Если общее количество ячеек дальности в массиве {S_j1} существенно превышает эту величину, то, очевидно, нет необходимости использовать весь этот массив и достаточно ограничиться его группой из М выборок. Эту группу целесообразно выбирать из конечной части массива {S_j1}, где величина отраженного целью сигнала мала и не может исказить результаты оценки. После определения статистических характеристик M_S и σ_S определяют величину C_N порога 6 накопления C_N=Qσ_S+M_S, где Q - коэффициент превышения порога над шумом, определяемый заранее из условия допустимой вероятности ложного измерения. Например, если для каждого измерения задана вероятность ложной тревоги F=0,01, то при равномерном распределении этого параметра вдоль трассы в каждой ячейке дальности вероятность ложной тревоги не должна превышать F_j=F/J, где J - количество ячеек дальности. Так, при J=1000 вероятность F_j=10^-5. Коэффициент Q определяется из условия 0,5-Ф(Q)=F_j, где

Для определения Q по заданному значению F_j можно воспользоваться приближенным соотношением

, с высокой точностью справедливым для Q>2.

Для указанного значения F_j=10^-5 величина Q~4,4.

В соответствии с предложением коэффициент Q изменяют в зависимости от дальности (от номера ячейки дальности) таким образом, чтобы в дальней зоне он уменьшался, обеспечивая более высокую вероятность обнаружения сигнала. При этом суммарная вероятность ложной тревоги во всем диапазоне не ухудшается.

Пример.

Количество ячеек дальности J=1000. Эти ячейки разбиты на два поддиапазона - ближний (I) в количестве 800 ячеек и дальний (II) в количестве 200 ячеек. Вероятности ложной тревоги в поддиапазонах F_I=0,002, F_II=0,008. F_I+F_II=0,01, как и в ранее рассмотренном случае с равномерным распределением вероятности F по ячейкам дальности. В рассматриваемом примере в дальнем поддиапазоне II вероятность F_j(II)=F_II/200=0,008/200=4·10^-5. В поддиапазоне I, соответственно, F_j(II)=F_I/800=0,002/800=2,5·10^-6. Коэффициенты Q для этих вероятностей соответственно равны:

Q_(II)=4; Q_(I)=4,6.

Это означает, что в дальней части диапазона измеряемых дальностей чувствительность улучается в Q/Q_(II)=4,4/4=1,1 раза, что ведет к соответствующему увеличению дальности действия дальномера. В ближней части диапазона чувствительность ухудшается в Q_(I)/Q=4,6/4,4=1,05 раза, что не влияет на качество измерений, поскольку это ухудшение компенсируется более значительным увеличением принимаемого сигнала: известно [1], что для малоразмерных целей его амплитуда обратно пропорциональна четвертой степени дальности, поэтому отношение амплитуд сигнала, соответствующих 800-й и 1000-й ячейкам дальности, равно (1000/800)⁴~2,5 раза, что значительно превышает потери за счет увеличения Q в этой области.

По окончании процесса накопления и выделения массива {S_j} его сравнивают с массивом {S_0j} по заранее установленному правилу, например, путем определения коэффициентов корреляции R(p) массивов {S_j} и {S_0j} при пошаговом сдвиге второго массива относительно первого на р=1,2,…Р_max шагов [5]. В результате формируют корреляционную функцию . Затем определяют шаг р=Р, на котором функция R(p) максимальна, и вычисляют дальность D до цели по формуле D-сРТ/2, где с - скорость света.

Для сокращения времени измерения рекомендуется осуществлять поиск порядкового номера шага Р, при котором значение R(P) оптимально, путем поэтапного приближения по методу деления отрезка пополам, а именно на каждом этапе поиска определяют оценки R(р_н) и R(р_в) на нижней р_н и верхней р_в границах зоны поиска и на следующем этапе зону поиска устанавливают между р~(р_в+р_н)/2 и тем из крайних значений р зоны поиска, оценка которого r(р) на данном шаге приближения наиболее оптимальна, причем на первом этапе поиска р_н=p(S_C)-t_И/T, а р_в=р_н+2t_и/T, где p(S_С) - номер ячейки дальности, в которой накопленная сумма S_j=S_С превысила установленный порог C_N.

Предлагаемый способ некогерентного накопления светолокационных сигналов обеспечивает измерение дальности при минимальном объеме накопления, при минимальном объеме статистических данных, используемых для определения оптимального режима накопления, а также за минимальное количество шагов. Сокращению объема накопления N существенно способствует также увеличение энергетического потенциала прибора, обусловленное увеличением длительности зондирующего импульса в пределах, допускаемых заданной разрешающей способностью: при этом увеличивается энергия зондирующего сигнала и уменьшается шум в приемном канале благодаря соответствующему сужению его полосы пропускания. В результате достигается максимально возможная оперативность измерения дальности при максимальной дальности действия и минимальных энергетических затратах.

Источники информации

1. В.А.Волохатюк, В.М.Кочетков, P.P.Красовский "Вопросы оптической локации". М., Изд-во "Советское радио", 1971 г., с.176.

2. Я.Д.Ширман, В.Н.Манжос «Теория и техника обработки радиолокационной информации на фоне помех». М., Изд-во «Радио и связь», 1981 г., с.70, 81.

3. Патент РФ №2359226 по заявке 2007137271/28 от 10.10.2007. «Способ некогерентного накопления светолокационных сигналов». - Прототип.

4. В.Е.Гмурман «Теория вероятностей и математическая статистика», М., Изд-во «Высшая школа», 1977 г.

5. Patent US No 5805468.

1. Способ некогерентного накопления светолокационных сигналов, включающий серию из N циклов зондирования, в каждом цикле зондирования производят посылку зондирующего светового импульса S₀(t,t₀), где t - текущее время, t₀ - момент излучения зондирующего импульса, квантуют время на отдельные дискреты длительностью Т, образуя тем самым ячейки дальности, в каждой из дискрет времени осуществляют прием отраженного сигнала S(t,t_D), где t_D - момент приема отраженного импульса, определяют его значение S_jm, накапливают значения S_jm в каждой j-й ячейке дальности путем формирования их сумм , и по массиву сумм {S_j} судят о задержке τ принятого сигнала относительно зондирующего импульса τ=t_D-t₀, по которой определяют дальность до цели D=сτ/2, где с - скорость света, j=1, 2, … J - порядковый номер ячейки дальности, начиная от момента t₀; J - количество ячеек дальности; m=1, 2, … N - порядковый номер зондирования, отличающийся тем, что устанавливают длительность t_и зондирующего импульса в пределах от 2Т до ΔТ_D, где ΔТ_D - заданная разрешающая способность по дальности, предварительно производят оцифровку зондирующего импульса путем определения его выборочных значений S_0j с периодом выборок, равным тактовому периоду Т, где j=1, 2, … К - порядковый номер выборки, начиная от момента t₀; K=t_и/T - количество выборок, и регистрации массива {S_0j} этих выборочных значений, а по завершении накопления пошагово сдвигают массив {S_j} относительно {S_0j}, на каждом шаге р=1, 2, … Р_max, проверяя степень их совпадения по заранее установленному критерию, например по коэффициенту корреляции где Р_max - максимальное число шагов, соответствующее диапазону измерения дальности, определяют порядковый номер шага Р, на котором степень совпадения массивов {S_j} и {S_0j} оптимально соответствует принятому критерию, и определяют дальность D до цели по формуле D=cPT/2, причем в процессе накопления определяют оценки среднеквадратического отклонения σ_S выборочных значений S_jm и их среднего значения M_S, устанавливают порог накопления C_N=Qσ_S+M_S, где Q - коэффициент превышения порога над шумом, определяемый из условия обеспечения максимальной вероятности правильного обнаружения в каждой ячейке дальности при заданной вероятности ложной тревоги во всем диапазоне измеряемых дальностей, и прекращают процесс накопления при количестве зондирований N, когда хотя бы в одной из ячеек дальности накопленная сумма S_j превысит пороговую величину С_N.

2. Способ по п.1, отличающийся тем, что в одном из массивов {S_jm}, например в массиве {S_j1}, выделяют группу статистически независимых выборочных значений в количестве М, и затем определяют оценки среднего значения M_S и среднеквадратического отклонения σ_S по формулам ; причем количество М выборочных значений в этой группе предварительно устанавливают из условия обеспечения заданной точности оценок, например с помощью уравнения гдеq - допустимая погрешность оценки;γ - надежность оценки; - плотность распределения случайной величины χ. - оценка величины обусловленного шумом среднеквадратического разброса выборок в массиве {S_j};σ>0 - непрерывный параметр, имеющий размерность σ_S.

3. Способ по п.1, отличающийся тем, что в начале измеряемого интервала дальностей коэффициент Q устанавливают с превышением относительно среднего значения, а по мере увеличения порядкового номера j уменьшают его таким образом, чтобы вероятность ложной тревоги во всем измеряемом диапазоне дальностей не превышала заданного предела, причем начальное превышение коэффициента Q и его значения, соответствующие текущей дальности, задают из условия соблюдения требуемой вероятности обнаружения сигнала в каждой из ячеек дальности.