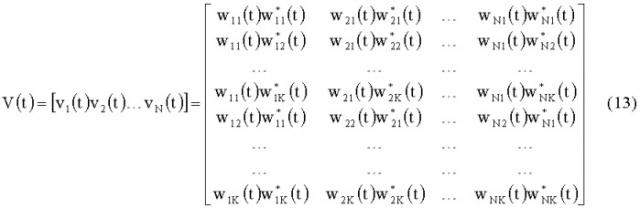Способ спектрального анализа электрического сигнала

Способ спектрального анализа электрического сигнала

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиоэлектроники, а именно - к спектральному анализу электрических сигналов.

Спектральный анализ относится к одной из важнейших задач обработки сигналов, причем особо актуально определение комплексного спектра, включающего амплитудный спектр и фазовый спектр, поскольку только комплексный спектр позволяет однозначно восстановить анализируемый сигнал. При этом наиболее просто получаемыми измерениями являются измерения мощности. Изобретение позволяет по измеренным мощностям на выходах гребенки фильтров определить комплексный спектр входного сигнала.

Известен способ спектрального анализа, позволяющий определять комплексный спектр сигнала [1]. Он основан на быстром преобразовании Фурье (БПФ). Способ состоит в том, что анализируемый сигнал s(t) дискретизируют с шагом дискретизации , где N - число дискретных выборок сигнала, Ω - точность спектрального анализа (т.е. шаг между дискретными значениями оценок спектральных составляющих), дискретные значения оцифровывают, после чего обрабатывают полученную выборку, основываясь на дискретном преобразовании Фурье и получают дискретизированный спектр сигнала

где k - номер спектральной дискреты, n - номер временной дискреты сигнала.

Этот способ позволяет достигать высоких точности и разрешения спектрального анализа при использовании достаточно длинной выборки сигнала.

Недостатком его является необходимость получения в цифровой форме достаточно длинной выборки (для приемлемой точности спектрального анализа) со стабильным шагом дискретизации. При этом шаг дискретизации T должен отвечать теореме Котельникова, т.е. быть по крайней мере в 2 раза меньше , где F_max - максимальная частота в спектре сигнала. То есть для высокочастотного сигнала частота выборок может потребоваться настолько высокой, что оцифровка их окажется нереализуемой.

Еще одним недостатком является то, что для увеличения точности спектрального анализа с помощью БПФ необходимо пропорционально увеличивать длину временной выборки. Действительно, т.к. и T увеличивать нельзя из соображений теоремы Котельникова, то для уменьшения шага дискретизации спектра Ω (увеличения точности спектрального анализа) необходимо увеличивать N, т.е. длину временной выборки сигнала, что приводит к увеличению времени спектрального анализа.

От указанных недостатков свободен способ спектрального анализа [2], основанный на пропускании анализируемого сигнала через гребенку селективных фильтров - прототип заявляемого способа. Способ-прототип состоит в том, что сигнал подают на гребенку селективных фильтров, настроенных на разные частоты в диапазоне контролируемых частот и проводят измерения мощностей сигналов на выходах фильтров гребенки.

Измерения мощностей вместо измерения комплексных сигналов проводят по следующей причине. В выходной сигнал любого фильтра-резонатора гребенки с разными весами входят все спектральные составляющие анализируемого сигнала, попавшие в полосу пропускания фильтра. Поэтому измерение комплексного сигнала на его выходе не позволяет сделать вывод о фазовой составляющей какой-либо гармоники, входящей в спектр анализируемого сигнала. В то же время, измерив мощности на выходах всех фильтров, получают информацию об амплитудном спектре анализируемого сигнала на частотах настройки фильтров. И при этом измерения мощности гораздо проще реализуются, чем измерения комплексного сигнала.

Основными преимуществами прототипа являются отсутствие проблем, связанных с дискретизацией анализируемого сигнала, а также отсутствие ограничений по частоте анализируемого сигнала, связанных с необходимостью применения аналого-цифрового преобразования с высокой и стабильной частотой выборок сигнала. Прототип может быть применен в более высокочастотном диапазоне, чем аналог на основе БПФ.

Главным недостатком прототипа является то, что он позволяет оценить только амплитудный спектр анализируемого сигнала, в то время как фазовый спектр остается неизвестным.

Другим недостатком является необходимость использования для высокоточного спектрального анализа большого числа фильтров, а для повышения разрешения частот - еще и обеспечения их высокой добротности. При высоких частотах анализируемого сигнала столь частую гребенку высокодобротных фильтров построить затруднительно.

Технической задачей данного изобретения является создание способа высокоточного определения комплексного спектра электрического сигнала по измеренным мощностям сигналов на выходах фильтров гребенки, причем гребенки, составленной из относительно малого числа низкодобротных фильтров-резонаторов.

Поставленная задача достигается тем, что в способе спектрального анализа, заключающемся в том, что анализируемый сигнал подают на гребенку селективных фильтров, настроенных на разные частоты в диапазоне контролируемых частот и измеряют мощности сигналов на выходах фильтров, согласно изобретению, до проведения измерений диапазон контролируемых частот разбивают на элементы разрешения, размер которых Ω определяется требуемыми точностью и разрешением спектрального анализа, определяют значения комплексных коэффициентов передачи каждого фильтра гребенки во всех элементах разрешения H_ik, i=1, 2, …N, k=1, 2, …, K где i - номер фильтра гребенки, k - номер элемента разрешения, N - число фильтров в гребенке, K - число элементов разрешения в диапазоне контролируемых частот, определяют весовые коэффициенты , где j - комплексная единица, ω_k - частота из k-го элемента разрешения, формируют из них весовую матрицу

размером K²×N, где ^* обозначает комплексное сопряжение, в некоторый момент времени t измеряют мощности на выходах всех фильтров гребенки и объединяют их в вектор измерений , где p_i(t) - измеренная мощность сигнала на выходе i-го фильтра, индекс T обозначает транспонирование, определяют вспомогательный вектор z размером K² из уравнения измерений или, при необходимости учитывать ошибки измерений, из уравнения , где n(t) - вектор ошибок измерений мощностей на выходах фильтров гребенки, из компонент полученного вектора , где ^ обозначает оценку соответствующей величины, формируют матрицу

, где ,

по компонентам первого столбца матрицы Q определяют комплексный спектр сигнала с точностью элемента разрешения в форме вектора

,

k-я компонента которого является оценкой комплексной спектральной составляющей анализируемого сигнала, приходящейся на k-й элемент разрешения.

Положительный эффект достигается за счет нового принципа спектрального анализа, основанного на использовании определенных априори значений комплексных коэффициентов передачи фильтров гребенки во всех элементах разрешения, на которые разбивается диапазон контролируемых частот, и размер которых выбирается тоже априори из соображений обеспечения требуемых точности и разрешения.

Заявляемый способ обладает двумя принципиальными особенностями. Во-первых, он позволяет по измеренным мощностям на выходах фильтров гребенки восстанавливать комплексный спектр анализируемого сигнала. Во-вторых, точность и разрешение спектрального анализа определяются размером элементов разрешения, на которые разбивается диапазон анализируемых частот, а не частотой гребенки фильтров и не их добротностью. То есть заявляемый способ позволяет при ограниченном числе низкодобротных фильтров достигать высоких точностей спектрального анализа и сверхразрешения частот.

Обоснование способа.

Пусть анализируемый сигнал описывается функцией времени s(t). Требуется определить его комплексный спектр S(ω), где ω - круговая частота.

Определим сигнал на выходе некоторого фильтра гребенки. Пусть свойства фильтра описываются комплексной передаточной функцией H(ω). Тогда спектр сигнала на выходе фильтра определится известным соотношением

G(ω)=H(ω)S(ω).

Выходной сигнал фильтра g(t) найдем, используя обратное преобразование Фурье:

Полагая, что спектр сигнала лежит в диапазоне контролируемых частот (ω_н,ω_k), изменим в (1) пределы интегрирования:

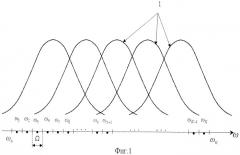
Разобьем диапазон контролируемых частот (ω_н,ω_k) на элементы разрешения, размер которых Ω определяется требуемыми точностью и разрешением спектрального анализа. Качественно соотношение полос пропускания фильтров гребенки и элементов разрешения в диапазоне контролируемых частот показано на фиг.1, где цифрой 1 отмечены зависимости от частоты модулей передаточных характеристик фильтров - амплитудно-частотные характеристики фильтров гребенки.

Определим значения комплексных коэффициентов передачи каждого фильтра гребенки во всех элементах разрешения H_ik, i=1, 2, …, N, k=1, 2, …, K, где i - номер фильтра гребенки, k - номер элемента разрешения, N - число фильтров в гребенке, K - число элементов разрешения в диапазоне контролируемых частот. Для этого каждому элементу разрешения поставим в соответствие некоторую частоту разрешения из этого элемента разрешения, например частоту, равную середине элемента разрешения ω₁, ω₂, …, ω_К, как показано на фиг.1. Значения комплексной передаточной функции рассматриваемого фильтра на всех частотах разрешения H_k=H(ω_k), k=1, 2, …, K и будут искомыми коэффициентами передачи.

Иными словами, проведем дискретизацию комплексной передаточной функции фильтра с шагом дискретизации Ω. С учетом сделанной дискретизации и разбиения диапазона контролируемых частот на элементы разрешения, заменим интеграл (2) суммой дискретных значений:

где dω заменено размером элемента разрешения Ω, а искомый спектр S(ω) заменен дискретными значениями спектральных составляющих, приходящихся на каждый элемент разрешения. При этом как H_k, так и S(ω_k) являются комплексными величинами.

Обозначим спектральную составляющую, приходящуюся на k-й элемент разрешения, как

а соответствующий k-му элементу разрешения весовой коэффициент как

С учетом (4a) и (4б) перепишем сумму (3) в виде

где

весовой вектор,

спектральный вектор.

Спектральный вектор (7) представляет искомый комплексный спектр сигнала, представленный в дискретизированном виде с шагом дискретизации Ω. Определив спектральный вектор (7), мы тем самым определим искомый спектр с точностью элемента разрешения Ω. Задача заключается в определении этого вектора по измеренным мощностям на выходах гребенки фильтров.

Перейдем к выражению, описывающему мощность выходного сигнала фильтра. В момент времени t эту мощность можно представить следующим выражением:

где , z_µ=s_i,s_l, , то есть

весовой вектор,

вспомогательный вектор, который необходимо определить для решения задачи.

Заметим, что вектор известен: он сформирован из K весовых коэффициентов (4б). Вспомогательный вектор z, хотя и не является искомым вектором s, однако однозначно определяется его компонентами.

Проведем в некоторый момент времени t измерения мощностей сигналов на выходах всех фильтров гребенки. Согласно (8) измерения эти можно представить следующим образом:

где N - число фильтров в гребенке a v_i(t) - весовой вектор i-го фильтра.

Объединим измеренные мощности в вектор измерений

а из весовых векторов фильтров гребенки сформируем весовую матрицу

размером K²×N, где w_nk(t) - комплексный коэффициент передачи n-го фильтра в k-м элементе разрешения.

С учетом (12) и (13), перепишем систему уравнений (11) в векторно-матричной форме:

При необходимости учитывать ошибки измерений уравнение (14) принимает вид

где n(t) - вектор ошибок измерений мощностей на выходах фильтров гребенки.

Определим вспомогательный вектор z.

При известных статистических характеристиках искомого вектора z и вектора ошибок оценка может быть найдена из уравнения (15) методом винеровского оценивания. При неизвестных статистических характеристиках решение может быть получено из уравнения (14) методом псевдообращения, как это изложено в [3].

Оценка методом псевдообращения определяется формулой

где индекс + обозначает псевдообратную матрицу.

Далее найдем искомый спектральный вектор s по компонентам полученного вектора . Согласно (10) структура вектора имеет вид

Сформируем из компонент вектора матрицу Q размером K×K:

где .

Определим теперь комплексный спектр сигнала с точностью элемента разрешения в форме спектрального вектора s. Этот вектор определим по компонентам матрицы Q. Согласно структуре вектора (17) перепишем (18) в детализованном виде:

Для определения спектрального вектора s используем первый столбец матрицы (19). Будем полагать, что спектральная составляющая в первом элементе разрешения имеет нулевую фазу. Тогда

,

где || обозначает модуль соответствующей величины, что в случае гармонического анализа равнозначно амплитуде.

При этом, получаем: из чего следует возможность определить первую компоненту вектора s:

Будем полагать, что оценка первой компоненты (20) - точная: . Тогда

и, следовательно,

Аналогично (21) найдем все K компонент искомого спектрального вектора. В итоге определим комплексный спектральный вектор, объединив полученные оценки (20), (21), и т.д.:

Каждая компонента вектора является оценкой комплексной спектральной составляющей анализируемого сигнала, приходящейся на соответствующий элемент разрешения. Оценка (22) является представлением комплексного спектра анализируемого сигнала, дискретизированного по элементам разрешения, т.е. это есть оценка комплексного спектра анализируемого сигнала с точностью элемента разрешения. Таким образом, точность спектрального анализа определяется размером выбранного априори элемента разрешения, а не количеством фильтров в гребенке и их добротностью.

Заявленный способ спектрального анализа позволяет достигать как высокой точности, так и сверхразрешения частот, которое определяется размером элемента разрешения и может быть гораздо меньше полосы пропускания фильтров, которой обусловлено разрешение в прототипе.

Преимущества предлагаемого способа по сравнению с прототипом следующие.

1. Способ позволяет по измеренным мощностям сигналов на выходах фильтров гребенки определять комплексный спектр сигнала, т.е. не только амплитудный, но и фазовый спектр, что в прототипе невозможно.

2. Способ позволяет осуществлять высокоточный спектральный анализ и достигать сверхразрешения частот, используя гребенку относительно малого числа низкодобротных фильтров, что упрощает техническую реализацию спектрального анализа.

3. Способ обеспечивает сокращение времени спектрального анализа, поскольку позволяет использовать небольшое число низкодобротных фильтров-резонаторов вместо большого числа высокодобротных в прототипе при одинаковых точности и разрешении, а, как известно, понижение добротность сопровождается уменьшением времени затухания собственных колебаний фильтра.

4. Способ ориентирован на цифровую обработку и позволяет получать оценку комплексного спектра анализируемого сигнала сразу в цифровой форме, что удобно для дальнейшей обработки.

Источники информации

1. Голд Б., Рэйдер Ч. Цифровая обработка сигналов. Пер. с англ., под ред. A.M.Трахтмана. - М., «Сов. радио», 1973, стр.190-192, 203-227.

2. Харкевич А.А. Спектры и анализ. - М., Государственное изд-во технико-теоретической литературы, 1952, стр.93-96 (прототип).

3. Самойленко М.В. Математические аспекты применения томографического подхода в обработке многоканальных сигналов. // Вестник Московского авиационного института, т.17, №3, 2010, стр.207-210.

Способ спектрального анализа электрического сигнала, заключающийся в том, что анализируемый электрический сигнал подают на гребенку селективных фильтров, настроенных на разные частоты в диапазоне контролируемых частот и измеряют мощности сигналов на выходах фильтров, отличающийся тем, что до проведения измерений диапазон контролируемых частот разбивают на элементы разрешения, размер которых Ω определяется требуемыми точностью и разрешением спектрального анализа, определяют значения комплексных коэффициентов передачи каждого фильтра гребенки во всех элементах разрешения H_ik, i=1, 2, …, N, k=1, 2, …, K, где i - номер фильтра гребенки, k - номер элемента разрешения, N - число фильтров в гребенке, K - число элементов разрешения в диапазоне контролируемых частот, определяют весовые коэффициенты , где j - комплексная единица, ω_k - частота из k-го элемента разрешения, формируют из них весовую матрицу размером К²×N, где * обозначает комплексное сопряжение, в некоторый момент времени t измеряют мощности на выходах всех фильтров гребенки и объединяют их в вектор измерений , где p_i(t) - измеренная мощность сигнала на выходе i-го фильтра, индекс T обозначает транспонирование, определяют вспомогательный вектор z размером К² из уравнения измерений p(t)=V^T(t)z или, при необходимости учитывать ошибки измерений, из уравнения p(t)=V^T(t)z+n(t), где n(t) - вектор ошибок измерений мощностей на выходах фильтров гребенки, из компонент полученного вектора , где ^ обозначает оценку соответствующей величины, формируют матрицу , где ,по компонентам первого столбца матрицы Q определяют комплексный спектр сигнала с точностью элемента разрешения в форме вектора ,k-я компонента которого является оценкой комплексной спектральной составляющей анализируемого сигнала, приходящейся на k-й элемент разрешения.