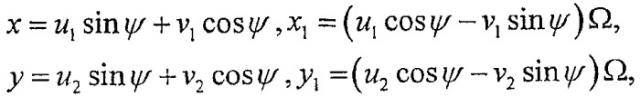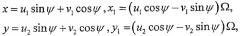Подавление поперечных вибраций электроцентробежного насоса посредством модулирования скорости вращения двигателя

Подавление поперечных вибраций электроцентробежного насоса посредством модулирования скорости вращения двигателя

Иллюстрации

Показать все

Реферат

Область применения

Настоящее изобретение относится к способу подавления поперечных вибраций в погружных электроцентробежных насосах, которые обычно применяются в нефтегазовой промышленности. В частности, изобретение относится к способу управления скоростью двигателя для подавления указанных вибраций.

Уровень техники

Погружные электроцентробежные насосы широко используются в нефтяной промышленности для механизированной добычи в нефтяных скважинах, которые не имеют достаточно давления для притока нефти на поверхность. Такие насосы обычно имеют двигательную секцию и насосную секцию, часто разделенные защитной секцией, включающей переходник и впуск насоса. В связи с типичными размерами нефтяных скважин двигатель и насос должны иметь сравнительно длинные и тонкие конструкции. Вал (или совокупность валов) проходит через двигатель, так что он поддерживает ротор изнутри как статорная секция, и далее проходит через насосную секцию, где на нем крепится последовательность рабочих колес, которые вместе с диффузорами закреплены на корпусе и образуют центробежный насос. Такие насосы обычно работают со скоростью вращения до 3000 об/мин, хотя предлагаются насосы и с большими скоростями.

Хотя насосы предназначены работать при по существу постоянной скорости вращения, при включении насоса существует период времени, когда насос работает на других скоростях. Поэтому обычно стараются уравновесить вращающиеся конструкции погружного электроцентробежного насоса при заданной скорости для предотвращения нежелательных поперечных вибраций.

Из практики известно, что поперечные вибрации погружного электроцентробежного насоса могут достичь нежелательного уровня. Значительные вибрации могут создаваться, например, на этапах включения или выключения насоса, когда он проходит через ряд резонансных частот, или во время типичных отклонений в рабочей скорости, когда спектр насоса содержит резонансные частоты, близкие к рабочей скорости. Увеличение уровня вибраций происходит из-за отклонения параметров насоса во время его работы. Типичными причинами увеличения вибраций насоса являются следующие.

Появление твердых отложений на вращающихся компонентах, что приводит к увеличению общей массы насоса и к сдвигу спектра критических частот в сторону низких частот (первоначально рабочие скорости находятся вне резонансных зон, но со временем они могут сместиться в указанные частотные зоны). Дисбаланс насоса также увеличивается в связи с неравномерностью осаждения твердых отложений на компонентах насоса.

Износ подшипников из-за изменений в характеристиках смазки, жесткости, относительного демпфирования, изменения в вязкости смазки, при этом в результате износа может также меняться геометрия подшипников, и т.д.

Неоднородность добываемой текучей среды (появление пузырьков газа, твердых частиц и т.д.).

Применение обычных гасителей вибраций для погружного электроцентробежного насоса считается нецелесообразным, поскольку отсутствует возможность настройки рабочей полосы частот гасителя вибраций, так как смещение критических частот в общем случае неизвестно.

Настоящее изобретение создает альтернативный способ подавления вибраций, который построен на управлении погружным электроцентробежным насосом.

Сущность изобретения

Согласно первому аспекту настоящего изобретения создан способ управления работой погружного электроцентробежного насоса, содержащий определение по меньшей мере одной рабочей скорости, при которой указанный насос испытывает поперечные вибрации неприемлемого уровня, и применение периодической модуляции рабочей скорости насоса для подавления его поперечных вибраций при работе насоса на определенной скорости.

Предпочтительно периодическая модуляция включает гармоническую добавку определенной рабочей скорости насоса, и способ содержит определение значений амплитуды и сдвига по фазе гармонической добавки, при которых подавляются поперечные вибрации насоса. Применяемая периодическая модуляция может определяться согласно формуле:

,

где - частота вращений, и - амплитуда и сдвиг по фазе гармонической добавки, - время, - число.

Предпочтительно периодическая модуляция выбирается для минимизации подавления крутильных колебаний в насосе.

Обычно периодическая модуляция вызывает изменение рабочей скорости, составляющее менее 5%.

Рабочая скорость, при которой насос испытывает поперечные вибрации неприемлемого уровня, может определяться математическим моделированием или экспериментально.

Способ может содержать мониторинг работы насоса для обнаружения поперечных вибраций неприемлемого уровня и применение модуляции рабочей скорости при обнаружении указанных вибраций.

Согласно второму аспекту настоящего изобретения создан погружной электроцентробежный насос, содержащий систему управления, работающую в соответствии со способом согласно первому аспекту изобретения.

Дальнейшие аспекты данного изобретения будут понятны из нижеследующего описания.

Краткое описание чертежей

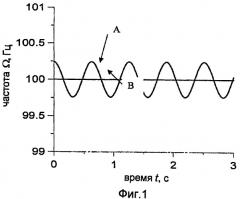
На фиг.1 показана кривая зависимости скорости вращения насоса от времени для примера применения в данном изобретении.

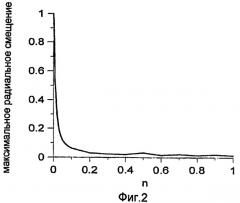
На фиг.2 показано максимальное радиальное смещение как функция параметра .

На фиг.3 показано максимальное радиальное смещение как функция параметра .

На фиг.4 показан график скорости вращения от времени для второго примера применения в данном изобретении.

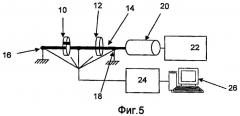
На фиг.5 показана схема установки для лабораторного тестирования.

На фиг.6 показан вал с несбалансированным диском, отклонение вала и плоскость диска (вид сверху), где показана плоскость координат и эксцентриситет диска.

На фиг.7 проиллюстрирована функция Бесселя первого рода.

На фиг.8 показана кривая зависимости амплитуды от времени для случая первой резонансной частоты (система без демпфирования).

На фиг.9 показан переходный процесс подавления вибраций для случая n=3, A=2,4.

На фиг.10 показана кривая зависимости амплитуды подавляемых вибраций от времени для первой резонансной частоты для случая n=3, A=2,4.

На фиг.11 показан переходный процесс подавления вибраций для случая n=0,6, A=2,4.

На фиг.12 показана кривая зависимости амплитуды подавляемых вибраций от времени для первой резонансной частоты для случая n=0,6, A=2,4.

На фиг.13 показан переходный процесс подавления вибраций для случая n=1, A=2,4.

На фиг.14 показана кривая зависимости амплитуды подавляемых вибраций от времени для первой резонансной частоты для случая n=1, A=2,4.

На фиг.15 показан переходный процесс подавления вибраций для случая n=2, A=2,7.

На фиг.16 показана кривая зависимости амплитуды подавляемых вибраций для первой резонансной частоты для случая n=2, A=2,7.

Варианты осуществления изобретения

Согласно способу настоящего изобретения при достижении поперечными вибрациями погружного электроцентробежного насоса критической величины генерируются дополнительные гармоники к постоянной частоте вращения насоса (например, просто используя генератор частот), и обеспечивают резкое сокращение таких нежелательных вибраций. Таким образом, вместо вращения с частотой , частота вращений насоса имеет зависимость согласно следующей формуле: ,

где - частота вращения, и - амплитуда и сдвиг по фазе дополнительной гармоники, - время, - число. Выбирая параметры и , можно получить различную степень гашения вибраций. Обычно - любое число, которое может быть простым, дробным или иррациональным. Пара параметров должна выбираться так, чтобы гармоника находилась между дозволенными пределами, поскольку определенные изменения в скорости вращения могут вызвать усиление крутильных вибраций. Эти параметры определяются по результатам математического моделирования и экспериментально.

Для определения момента активации системы подавления вибраций (ее отключения) желательно иметь обратную связь от насоса относительно уровня вибраций. Это достигается, например, прямым или косвенным измерением вибраций.

Примером гармоники для случая =100 Гц (то есть 100 об/с), с параметрами =0,1, =2,4, =0, будет функция показанная на фиг.1, которая показывает эволюцию скорости вращения от времени. Линия A соответствует рабочей скорости/частоте (100 Гц/100 об/мин), а линия B описывает рабочую скорость после использования периодической модуляции. В этом случае максимальные изменения в скорости вращения составляют 0,5%.

Для иллюстрации эффективности подавления вибраций на фиг.2 показано максимальное радиальное смещение как функция параметра для случая A=2,4, а на фиг.3 - как функция параметра A для случая n=0,2. В этом случае система вращения моделируется в виде вала с одним несбалансированным диском, помещенным в центре системы (см. фиг.6). Максимальное радиальное смещение на фиг.2 и фиг.3 разделено на максимальное радиальное смещение для первой характерной частоты вибраций, определяемой как , где - жесткость при изгибе, а - масса диска. Вал с одним диском является довольно простой моделью; для предсказания уровней вибраций в насосе потребуется более сложная модель, поскольку насос имеет десятки масс (рабочие колеса) и несколько радиальных подшипников. Радиальное смещение для этой модели оказывается выше, чем для реального погружного электроцентробежного насоса, поскольку все массы рабочих колес уменьшены до одной большой массы. Получение аналитических решений для модели многих масс является математически сложной задачей и поэтому не применятся в рамках настоящего технического решения. Вместе с тем, упрощенная модель обеспечивает хорошую количественную оценку возможности снижения радиальных вибраций по сравнению с самыми большими амплитудами, которые имеют место для первой характерной частоты .

В пределах изменений величин и для случаев, отображенных на фиг.2-3, вариации в скорости вращения системы не превышают 5%, как видно из таблицы 1.

Таблица 1 Изменение скорости вращения как функция параметров A и n
	2,4	2,4	0,1	6,0
	0,1	1	0,2	0,2
Изменение скорости вращения	0,5%	5%	0,04%	1,5%

Анализ кривых на фиг.2 и фиг.3 приводит к следующим заключениям.

Чем больше параметр , тем лучше подавление вибраций (см. фиг.2). Поэтому разумно выбирать высокие значения для . Но это значение прямо связано с частотой добавочной гармоники. Например, для случая A=2,4 и n=1 мы имеем . Частота в 10 раз выше, чем для случая n=0,1 (см. фиг.4). Такого высокочастотного изменения трудно добиться из-за инерции насоса. Таким образом, должно выбираться таким, чтобы полученная вариация частоты была достижима на конкретном насосе. Другая величина, которую следует контролировать, - это уровень крутильных вибраций. Добавлением гармоники для подавления радиальных вибраций следует избегать генерации крутильных вибраций, или, при их возникновении, их уровень должен быть низким и не создавать проблемы.

Существует ряд величин параметра A, для которых эффективность подавления вибраций является оптимальной (см. два минимума функции, изображенной на фиг.3). Это связано со свойствами функции Бесселя (фиг.7), которая дает решение математической модели. Подавление вибраций будет максимальным, когда величины A совпадают с нулями функции Бесселя. Список нулей функций Бесселя можно найти в многочисленных справочниках по математическим функциям (например, Abramovitz M., Stegun I.A., Handbook of Mathematical Functions. New York: Dover; 1972), и их можно использовать для определения величин A. Как обычно, при выборе величины A следует учитывать проблему с крутильными вибрациями.

Представленные выше вычисления основаны на линейной модели в приближении первого («основного») вида резонанса. Динамика реальных погружных электроцентробежных насосов описывается большим количеством нелинейных уравнений, которые учитывают не только первый вид резонанса, но и более высокие виды. В качестве альтернативы сложной математике можно выполнить лабораторные тесты, чтобы выяснить следующее:

проверить эффект подавления вибраций не только для первого вида резонанса, но и для более высоких гармоник;

изучить эффект добавочных гармоник на уровни крутильных вибраций;

оптимизировать выбор параметров A и n;

изучить изменения сил, действующих на подшипники, расположенные на валу;

изучить влияние небольших вариаций массы и дисбаланса на выбранную пару параметров A и n (моделирование осаждения твердых отложений может привести к увеличению общей массы вращающихся деталей насоса и увеличить дисбаланс рабочих колес);

утвердить процедуру подавления вибраций для различных углов наклона вала (моделирование наклонных скважин).

Перед испытанием такой сложной структуры, как погружной электроцентробежный насос, следует провести лабораторные испытания. На фиг.5 показана лабораторная установка для тестирования, состоящая из несколько несбалансированных дисков 10, 12, помещенных на валу 14, размещенном на подшипниках 16, 18 и приводимом во вращение электрическим двигателем 20. Электрический двигатель 20 подсоединен к генератору 22 переменной частоты, который может генерировать необходимую гармоническую добавку к постоянной или переменной частоте вращения. Несколько видов датчиков 24 (бесконтактные датчики приближения, датчики скорости, динамометрические датчики) регистрируют и передают данные (смещение оси вала, амплитуды радиальных и крутильных вибраций, нагрузку на подшипники) на компьютер 26 для анализа.

Таким образом, изобретение характеризуется следующими признаками и имеет следующие преимущества:

два управляющих параметра A и n могут быть получены через математическое моделирование и/или эксперимент;

ожидаемая вариация в скорости вращения насоса составляет менее 5%;

гармоническая добавка должна быть минимальной для предотвращения крутильных вибраций;

отсутствует необходимость изменения конструкции насоса;

требуется мониторинг или оценка вибраций;

настоящее изобретение может быть частью активной системы управления.

Математическое моделирование подавления вибраций насоса в случае непостоянной скорости вращения может основываться на рассмотрении динамической системы, которая управляет изгибающими вибрациями ротора, состоящего из вала с несбалансированным диском, приводимого во вращение источником мощности. Диск имеет эксцентриситет (центр масс удален от геометрического цента диска). Вал закреплен на концах с помощью подшипников. Точка означает геометрический центр диска, точка означает центр масс, а точка означает ось для неискаженного вала.

Когда ротор проходит через область резонанса, к постоянному моменту вращения добавляется гармоническая компонента. Такая гармоническая добавка допустима также и в нормальном рабочем режиме, если управляющая система показывает нежелательное увеличение вибраций. В обоих случаях постоянная частота вращения подвергается гармонической модуляции, и основные уравнения имеют следующий вид:

Здесь и - внешнее и внутреннее подавление вибраций, соответственно, - жесткость на изгиб для вала, - угол вращения, - характерная частота ротора, - частота вращения, и - амплитуда и сдвиг по фазе для гармонической добавки, - число. Для удобства в приведенной системе используются безразмерные переменные и параметры; , и производная берется по безразмерному времени

Предположим, что коэффициенты внешнего и внутреннего подавления вибраций и эксцентриситет ротора малы:

,

где µ<<1 - малый параметр. В таком случае система уравнений принимает следующий вид:

Здесь .

Целью является следующий вопрос: можно ли и как выбрать параметры модулирования такими, чтобы амплитуда изгибных вибраций была минимизирована?

Получена система из двух неавтономных линейных осцилляторов. Каждый из осцилляторов можно представить как резонансный фильтр с частотой , которая соответствует первой резонансной гармонике ,.

Эти функции можно разложить в ряды Фурье с коэффициентами , представляющими функции Бесселя первого рода для целочисленного аргумента. Естественно, поскольку модель считается линейной, то и решения тоже можно представить в виде рядов Фурье. Если первая гармоника, имеющая самую высокую амплитуду, будет подавлена благодаря правильному выбору параметров модуляции, тогда амплитуды остающихся гармоник будут иметь величины порядка ~µ<<1. Это объясняется фильтрующими свойствами осцилляторов. Это означает, что максимальные радиальные смещения будут иметь тот же порядок: ~µ (заметим, что являются функциями многих частот). Итак, целью является подавление первой гармоники.

Прямое решение этой задачи следующее: поиск решения начальной системы в виде рядов Фурье с неопределенными коэффициентами, определение этих коэффициентов и минимизация амплитуды первой гармоники. Вместе с тем, должна быть обеспечена стабильность решения. Обе части задачи достаточно стандартны, хотя и математически сложны. Для объединения двух задач в одну следует применить метод усреднения.

Можно представить изменения переменных в следующем виде:

и получить систему в следующем виде:

Величины всех переменных

строго зависят от параметра . Правые части уравнений для усредненной системы должны быть различны для различных .

По этой причине необходимо рассмотреть три качественно различных случая.

Случай 1. является целым числом в интервале , или дробным числом в интервале , или иррациональным числом.

Усредняя систему по быстро изменяющейся фазе и подставляя новую переменную времени: , мы получаем уравнения в первом приближении по параметру малости в следующем виде:

Здесь - функция Бесселя первого рода (см. фиг.7). В этом случае уравнения независимы от сдвига по фазе .

Величина , где являются координатами равновесия для этой линейной системы, есть амплитуда первой гармоники. Нашей целью является минимизация этой величины.

Полученная система имеет следующее свойство: в фазовом пространстве этой системы существует стабильное инвариантное множество . В самом деле, эта система уравнений, переписанная для переменных , имеет вид

Производная для функции Ляпунова , вычисленная для этой системы, выглядит как . В равновесии мы имеем ; таким образом, целочисленное множество является устойчивым.

Указанное свойство позволяет рассмотреть систему на множестве , что дает уравнения:

Величины для равновесных координат системы пропорциональны . Амплитуда первой гармоники является минимальной для минимальных величин из интервала для допустимых величин амплитуды модуляции . Амплитуда первой гармоники равна нулю (полное подавление вибраций) для всех , для которых . Функция Бесселя имеет бесконечное количество нулей. В частности, первый ноль соответствует случаю А=2,4 (минимальная величина). Подставляя в полученную систему А=2,4, получаем решение с устойчивым равновесием.

Таким образом, выбрав амплитуду А=2,4, при любом целом числе или иррациональном числе и при любом сдвиге по фазе (например, ) получается ситуация полного подавления первой гармоники для изгибных вибраций ротора. В этом случае амплитуда изгибных вибраций становится порядка ~µ<<1.

Далее применяются следующие безразмерные параметры:

.

На фиг.8 отложена амплитуда для первой резонансной частоты в случае недемпфированной системы (т.е. ) как функция времени.

На фиг.9-12 показаны переходные процессы для процесса подавления вибраций (слева) и изменения амплитуды подавляемых вибраций как функции времени (справа) в случае А=2,4 и n=0,6, А=2,4, соответственно. На этих диаграммах можно увидеть, что отношение между максимальными амплитудами вибраций (то есть максимальное радиальное смешение ротора от вертикальной оси) по сравнению с ситуацией без подавления вибраций составляет 2500 и 50, соответственно.

Случай 2. (модуляция на частоте ротора). В этом случае система усреднения записывается в следующем виде:

Равновесие такой системы является устойчивым (соответствующая однородная система имеет устойчивое целое множество для устойчивой системы, помещенной в это множество, см. выше). Равновесие имеет нулевые координаты независимо от фазы , если . Однако такая система является нестабильной. В отличие от предыдущего случая, для случая нет таких величин , чтобы обеспечить полное подавление первой гармоники.

На фиг.13-14 показан переходный процесс подавления вибраций (фиг.13) и изменения амплитуды подавляемых вибраций в зависимости от времени для первой резонансной частоты (фиг.14) для случая А=2,4. Для обоих случаев отношение исходной максимальной амплитуды к подавленной амплитуде составляет 6,67.

Случай 3. (модуляция с двойной частотой вращения ротора). В этом случае система после усреднения записывается в следующем виде:

На фиг.15-16 показан переходный процесс подавления вибраций (фиг.15) и изменения амплитуды подавляемых вибраций как функции времени для первой резонансной частоты (фиг.16) для случая параметров А=2,7. Отношение подавления амплитуд в обоих случаях составляет 16,67.

Заметим, что в случае целых n=1, 2 подавляемые вибрации являются квазигармоническими, а в случае дробного или подавляемые вибрации являются периодическими, но не гармоническими.

Очевидны также другие варианты осуществления настоящего изобретения.

1. Способ управления работой погружного электроцентробежного насоса, содержащий определение, по меньшей мере, одной рабочей скорости, при которой насос испытывает поперечные вибрации неприемлемого уровня, и применение периодической модуляции посредством генератора переменной частоты для изменения рабочей скорости насоса для подавления его поперечных вибраций при работе насоса на определенной скорости.

2. Способ по п.1, в котором периодическая модуляция включает гармоническую добавку определенной рабочей скорости насоса.

3. Способ по п.2, содержащий определение значений амплитуды и сдвига по фазе гармонической добавки, при которых подавляются поперечные вибрации насоса.

4. Способ по п.3, в котором применяемая периодическая модуляция определяется согласно формуле: ,где Ω - частота вращений; и ψ₀ - амплитуда и сдвиг по фазе гармонической добавки;t - время;n - число.

5. Способ по любому из предыдущих пунктов, в котором периодическая модуляция выбирается для минимизации подавления крутильных вибраций насоса.

6. Способ по п.1, в котором периодическая модуляция вызывает изменение рабочей скорости насоса, составляющее менее 5%.

7. Способ по п.1, в котором рабочая скорость, при которой насос испытывает поперечные вибрации неприемлемого уровня, определяется из математического моделирования.

8. Способ по п.1, в котором рабочая скорость, при которой насос испытывает поперечные вибрации неприемлемого уровня, определяется экспериментально.

9. Способ по п.1, содержащий мониторинг работы насоса для обнаружения поперечных вибраций неприемлемого уровня и применение периодической модуляции для изменения рабочей скорости насоса при обнаружении указанных вибраций.

10. Погружной электроцентробежный насос, содержащий систему управления, работающую в соответствии со способом по любому из пп.1-9.