Способ прогнозирования движения объекта швартовки

Способ прогнозирования движения объекта швартовки

Иллюстрации

Показать все

Реферат

Изобретение относится к водному транспорту и может быть использовано для безопасной швартовки швартующегося судна к объекту швартовки, а также для слежения и контроля за движением плавучих объектов и их идентификации в районе плавания.

Одним их важнейших условий безопасного выполнения швартовных операций к объекту швартовки, находящемуся в постоянном движении (плавучее гидротехническое сооружение, судно, стоящее на якоре, дрейфующее судно и т.п.), является наличие у швартующегося судна возможности непрерывно прогнозировать характер движения объекта швартовки вне зависимости от погодных условий и времени суток в районе выполнения швартовной операции [10], [11], [12]. При этом необходимо учитывать факторы, влияющие на особенности движения объекта швартовки. К указанным факторам, прежде всего, следует отнести: текущие гидро- и аэродинамические характеристики объекта швартовки, ветер, волнение, течение и др.

Для выполнения указанного выше условия безопасного осуществления швартовной операции швартующегося судна к объекту швартовки, находящемуся в постоянном движении, швартующемуся судну необходимо иметь базовую математическую модель объекта швартовки и в непрерывном режиме получать информацию об измеренных на объекте швартовки текущих значениях динамических параметров, отражающих характер его движения.

При этом за базовую математическую модель объекта швартовки принимают математическую модель, описывающую динамические свойства объекта швартовки без учета текущих значений параметров, характеризующих его посадку в воде, а также параметров, характеризующих состояние внешней среды в районе выполнения швартовной операции. Получение базовой математической модели, практически, любого плавучего объекта не является сложной технической и математической задачей [2], [3], [9], более того, в качестве базовой модели неизученного объекта швартовки может быть использована математическая модель аналогичного изученного объекта швартовки.

Динамическими параметрами, отражающими характер движения объекта швартовки, являются его линейное продольное и линейное поперечное ускорения, а также угловое ε_k ускорение. Текущие значения динамических параметров, отражающих характер движения объекта швартовки, могут быть измерены с использованием одного (универсального) акселерометра, одновременно измеряющего все указанные ускорения или нескольких акселерометров, каждый из которых измеряет только одно ускорение.

Наличие на швартующемся судне базовой математической модели объекта швартовки и его текущих значений линейных и углового ускорений позволяет непрерывно идентифицировать математическую модель объекта швартовки и прогнозировать характер его движения в данных условиях выполнения швартовной операции.

Технический результат, на достижение которого направлено заявляемое изобретение, состоит в повышении точности и безопасности выполнения швартовной операции к плавучему объекту, находящемуся в движении.

Технический результат достигается за счет того, что швартующееся судно использует идентифицированную математическую модель плавучего объекта швартовки для прогнозирования характера его движения на расстоянии.

Сущность способа заключается в следующем.

При выполнении швартующимся судном швартовной операции к борту плавучего подвижного объекта (объект швартовки, например, гидротехническое сооружение, дрейфующее судно, судно, стоящее на якоре, и др.), используют базовую математическую модель объекта швартовки для компьютерного моделирования при прогнозировании его движения в ходе швартовной операции. Эта модель представляет собой систему дифференциальных уравнений, общий вид которых в соответствии с данными, представленными в работах [1], [2], [3], [8], [9], следующий:

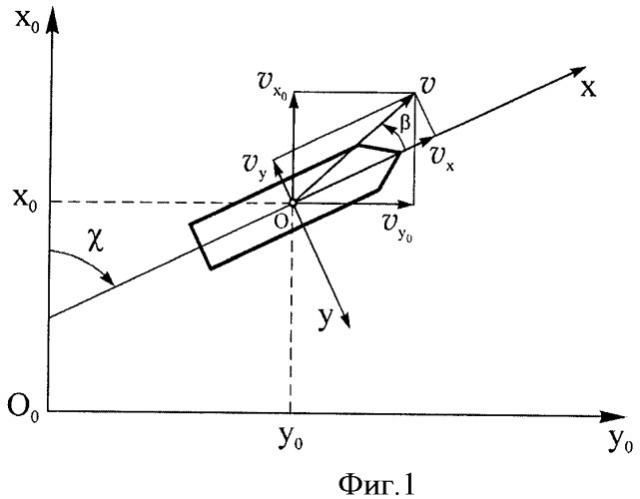
где υ_х, υ_y - проекции вектора линейной скорости в центре тяжести (ЦТ) объекта швартовки на продольную 0Х и поперечную 0Y оси, соответственно (см. Фиг.1);

ω - угловая скорость объекта швартовки;

C₁, С₂, С₃, С_m - параметры математической модели [1], [2], [3], [8], [9].

В процессе движения объекта швартовки с помощью акселерометров в реальном масштабе времени измеряют линейные продольное , поперечное и угловое ε_k ускорения объекта швартовки N раз за цикл обработки продолжительностью Т и шагом Δt, так что

Измеренные на объекте швартовки значения ускорений с использованием компьютерной системы Wi-Fi [4], [6], [7] передают на швартующееся судно.

По измеренным значениям ускорений находят соответствующие значения линейных и угловой скоростей:

Рассчитывают невязки Δ_k, т.е. разности между левой и правой частями дифференциальных уравнений движения судна (1) в момент k-го измерения:

Как следует из уравнений (1), (4), количество идентифицируемых параметров равно m.

Для определения значений параметров математической модели объекта швартовки С₁, С₂, С₃, С_m строится взвешенная сумма квадратов невязок:

здесь ρ - вес уравнения в системе (1) (0≤ρ≤1,0), ρ устанавливается по приоритету оператором в соответствии со степенью важности уравнения при прогнозировании движения объекта швартовки. В случае равнозначности уравнений в системе (1) ρ₁, ρ₂, ρ₃ можно принимать равными 1,0.

Сумму квадратов невязок минимизируют. Для этого сумму дифференцируют по идентифицируемым параметрам C_q (q=1, …, m) и частные производные приравнивают к нулю, тем самым образуется система нормальных уравнений, состоящая из m уравнений по количеству идентифицируемых параметров:

Систему уравнений (6) решают методом последовательных приближений или Зейделя [5], если она линейная. Результатом решения системы уравнений (6) будут текущие значения параметров математической модели объекта швартовки (1), т.е. идентифицированные параметры.

Далее цикл измерений и идентификацию параметров базовой математической модели объекта швартовки повторяют, что обеспечивает их постоянное обновление. Постоянно обновляющиеся параметры математической модели объекта швартовки делают математическую модель адекватной текущим условиям выполнения швартовной операции, что позволяет использовать идентифицированную математическую модель объекта швартовки для прогнозирования его движения в процессе выполнения швартовной операции швартующимся судном.

Литература

1. Басин A.M. Ходкость и управляемость судов / A.M. Басин. - М.: Транспорт, 1967. - 255 с.

2. Васильев А.В. Управляемость судов: учеб. пособие / А.В.Васильев. - Л.: Судостроение, 1989. - 328 с.

3. Гофман А.Д. Движительно-рулевой комплекс и маневрирование судна: справочник / А.Д. Гофман. - Л.: Судостроение, 1988. - 360 с.

4. Григорьев В.А. Сети и системы радиодоступа / В.А. Григорьев, О.И. Лагуненко, Ю.А. Распаев. - М.: Эко-Тренз, 2005. - 384 с.

5. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). М.: Наука. 1974. 831 с.

6. Олифер В.Г. Компьютерные сети, принципы, технологии, протоколы: Учебник для вузов. 3-е изд. / В.Г. Олифер, Н.А. Олифер. - Спб.: Питер, 2006. - 958 с.

7. Педжман Л. Основы построения беспроводных локальных сетей стандарта 802.11.: Пер. с англ. / Л.Педжман. - М.: Издательский дом «Вильямс», 2004. - 304 с.

8. Соболев Г.В. Управляемость корабля и автоматизация судовождения / Г.В. Соболев. - Л.: Судостроение, 1976. - 478 с.

9. Справочник по теории корабля. В 3 т. Т.3: Управляемость водоизмещающих судов. Гидродинамика судов с динамическими принципами поддержания / под ред. Я.И. Войткунского. - Л.: Судостроение, 1985. - 544 с.

10. Тихомиров В.П. Управление маневрами корабля / В.П. Тихомиров. - М.: Воениздат, 1963. - 339 с.

11. Цурбан А.И. Швартовные операции морских судов / А.И. Цурбан, A.M. Оганов. - М.: Транспорт, 1987. - 176 с.

12. Юдин Ю.И. Совершенствование управления судном при выполнении швартовых операций на ходу в открытом море: автореф. дис.…канд. техн. наук / Ю.И.Юдин; Мурман. высш. инж. мор. уч-ще. - Мурманск, 1987. - 24 с.

1. Способ прогнозирования движения объекта швартовки, заключающийся в том, что на объекте швартовки с помощью акселерометров в реальном масштабе времени измеряют его линейное продольное, линейное поперечное и угловое ускорения, затем эти данные передают на швартующееся судно, используя значения ускорений объекта швартовки и его базовую математическую модель, на швартующемся судне идентифицируют текущие значения параметров математической модели объекта швартовки, далее цикл измерений и идентификацию параметров базовой математической модели объекта швартовки повторяют.

2. Способ по п.1, отличающийся тем, что передачу измеренных на объекте швартовки значений ускорений осуществляют с использованием компьютерной системы Wi-Fi.