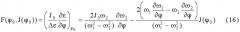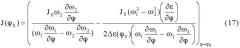Способ определения приведенного момента инерции механизма

Способ определения приведенного момента инерции механизма

Иллюстрации

Показать все

Реферат

Изобретение относится к измерению физических величин и может быть использовано в машиностроении, где применяются механизмы с переменным приведенным моментом инерции звеньев. Это металлорежущие и деревообрабатывающие станки, робототехника, горное и нефтедобывающее оборудование.

Технический результат изобретения - определение приведенного к заданной оси переменного момента инерции механизма как функции угла поворота звена приведения.

Известен способ определения момента инерции механизма, где исходным источником информации является время (Патент №2019797, БИ №17 за 1994 год).

Недостаток способа в том, что он применяется только для механизмов с постоянным моментом инерции.

Наиболее близкий по технической сущности способ определения приведенного момента инерции механизма заключается в изменении инерционных свойств механизма путем присоединения дополнительного маховика с известным моментом инерции и измерении угловой скорости звена приведения (Патент №2025679, БИ №24 за 1994 год).

Недостаток способа в том, что он не позволяет определить приведенный переменный момент инерции механизма как функцию угла поворота звена приведения. Дело в том, что приведенный переменный момент инерции является периодической функцией угла поворота φ звена приведения [1]. Закон сохранения момента количества движения в форме

J(φ)ω₁=J(φ)ω₂+J₂ω₂,

может быть применен только при равенстве в выражениях J(φ)ω₁ и J(φ)ω₂ моментов инерции J(φ) в обоих случаях. Но для этого необходимо контролировать угловую координату φ и только при одном и том же значении φ=φ₀ можно говорить о применении закона сохранения количества движения.

Однако в описании способа контроль φ вообще не предполагается. Более того, ω₁ и ω₂ - это тоже переменные функции угловой координаты φ, например, из-за переменного момента инерции, имеющие в своем составе колебательную компоненту [1]

ω₁=ω₁(φ), ω₂=ω₂(φ)

В выражениях J(φ)ω₂(φ)и J₂ω₂(φ) угловые скорости в каждом из этих выражений могут совпасть между собой при некотором φ₁ случайно. Но это φ₁ должно быть равно еще и φ₀, чтобы можно было применять указанный выше закон.

Следовательно, согласование условий измерения необходимо проводить одновременно по скорости ω₂(φ) и углу поворота φ звена приведения. Только в этом случае верно равенство для моментов количества движения. Таким образом, предлагаемый способ реализуем, если J(φ) величина постоянная и не зависит от φ. В этом случае угловые скорости не зависят от φ (от влияния переменного момента инерции) и можно говорить о монотонном режиме движения механизма и монотонно убывающем характере изменения скоростей ω₁ и ω₂, на чем и построен предложенный выше способ.

Заявленный технический результат достигается тем, что дополнительно измеряют в дискретной форме угол φ_i поворота звена приведения (i=0, 1, 2, …N, i - порядковый номер отверстия на диске фотоэлектрического датчика), а также измеряют изменение углового ускорения Δε(φ_i) звена приведения, например кривошипа, вызванное присоединением пробного груза, а величину приведенного момента инерции J(φ) определяют как функцию угла поворота звена приведения из решения численным методом дифференциального уравнения

с начальным условием

где угол φ₀ выбирается таким, при котором измеренные угловые скорости ω₁(φ₀) и ω₂(φ₀) максимально совпадут между собой, т.е.

.

Величина J₀ - момент инерции пробного груза, закрепляемого на кривошипе; ω₁(φ_i) и ω₂(φ_i) - измеряемые одновременно с φ_i угловые скорости.

Для измерения углов, скоростей и ускорений применяется прецизионный фотоэлектрический способ, описанный в работе [2]. Значения угловых скоростей ω₁(φ_i) и ω₂(φ_i), как функций угла φ_i, получаются данным методом сразу в дискретной форме в виде таблицы соответствия, что удобно для операций численного дифференцирования и интегрирования.

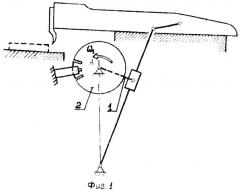
Соотношение между двумя последующими значениями φ₁ и φ_i+1 равно φ_i+1=φ_i+Δφ, а - угол между двумя соседними отверстиями на диске 2 фотоэлектрического датчика (Фиг.1); N=200-500 - количество отверстий на диске 2, модулирующих световой поток.

Заявленный способ состоит в следующем.

Исследуемый механизм, например металлорежущий строгальный станок, показанный на фиг.1, работает на холостом ходу в установившемся режиме. Угловая скорость ω₁ кривошипа 1 - звена приведения, меняется около среднего значения. Колебания скорости имеют установившийся характер.

Дифференциальное уравнение движения механизма, учитывающее зависимость приведенного момента инерции механизма J(φ) от угла поворота кривошипа φ имеет вид [1]

Поскольку ω₁=ω₁(φ(t)) - сложная функция от t, то

Окончательно, уравнение принимает вид

Функция J(φ) периодическая по φ (например, с периодом 2π). В течение периода изменения J(φ) измеряется угловая скорость кривошипа ω₁=ω_i как функция угла φ_i в виде дискретных значений, которые заносятся в память ЭВМ. Здесь же находятся производные известным численным методом [3].

В итоге, измеренные и рассчитанные значения в памяти образуют таблицу соответствия:

в которой N строк.

Таким образом, в уравнении (3) известны функции и .

По завершении периода изменения функции J(φ), измерения заканчиваются и механизм останавливается.

К звену приведения, в данном случае - кривошипу, жестко крепится маховик - инертная масса с известным моментом инерции J₀ и уравновешенная относительно оси вращения кривошипа. Уравновешивание необходимо для сохранения неизменными гравитационных сил веса звеньев исследуемого механизма, которые также приводятся к оси кривошипа в виде момента М(φ_i) и которые влияют на неравномерность угловой скорости ω₁(φ_i). Момент М(φ_i) входит в состав правой части уравнения (3).

Станок включается в работу на холостом ходу в установившемся режиме. Средняя скорость кривошипа максимально должна совпадать со средней скоростью в первом эксперименте, т.е. ω_1cp=ω_2ср. Этим обеспечивается постоянство характеристики двигателя в окрестности ω_ср.

Необходимо отметить, что установка маховика изменила только инерционные свойства механизма на постоянную величину J₀. Все остальные силовые факторы остались без изменения.

Дифференциальное уравнение для этого механизма имеет вид

Установившиеся колебания скорости ω₂(φ) около среднего значения стали меньше по амплитуде и частоте.

В правой части (5) стоит характеристика двигателя, а также приведенный момент сил веса звеньев механизма.

Движение механизма в окрестности скорости ω_2сp=ω_1cp позволяет рассматривать правую часть в уравнении (5) совпадающей с правой частью уравнения (3). Тогда с учетом равенства: , получим

После преобразований получаем дифференциальное уравнение первого порядка

Приводим выражение (7) к стандартному виду, удобному для численного интегрирования

Уравнение (8) решается любым известным численным методом, например, по формуле Эйлера:

где Δφ - шаг численного интегрирования, равный углу между двумя соседними отверстиями на диске фотоэлектрического датчика.

Для решения (8) или (9) необходимо задать начальные условия, т.е. при некотором φ₀ необходимо знать начальное значение момента инерции J(φ₀). Для определения J(φ₀) рассмотрим следующую производную: , где ε(φ) - угловое ускорение кривошипа, т.е. (см.формулу 2). Величина производной может быть найдена при любом конкретном значении φ₀ из следующих значений для приращений Δε и ΔJ:

Но ΔJ - это приращение (увеличение) инерционных свойств механизма на дополнительный известный момент инерции J₀, т.е. ΔJ=J₀.

Величина Δε - это изменение углового ускорения кривошипа, вызванное изменением инерционных масс, которое определяется как разность угловых ускорений: ε₁(φ₀) - измеренное ускорение кривошипа до установки маховика,; ε₂(φ₀) - после установки

Значения ε₁(φ) и ε₂(φ) выбираются для одного и того же положения кривошипа φ₀. Этим обеспечивается совпадение приведенных моментов от сил веса звеньев механизма. Кроме того, φ₀ выбирается так, чтобы угловые скорости φ₁(φ₀) и ω₂(φ₀) максимально совпадали между собой. В итоге:

С другой стороны, частная производная - равна отношению производных:

Частная производная углового ускорения ε(φ) по φ равна

Функции и - находятся численным методом и производная может быть найдена для любого φ, в том числе для заданного φ₀.

Из (13) находим

Определив , одновременно находится из (8) функция F(φ₀, J(φ₀)

Равенство (16) рассматриваем как уравнение относительно J(φ₀), поскольку значения всех остальных функций для φ=φ₀ известны

Это значение J(φ₀) совместно с дифференциальным уравнением (8) однозначно определяют функцию изменения приведенного к оси кривошипа момента инерции J(φ).

В качестве примера, алгоритм последовательного вычисления величины J(φ) методом Эйлера следующий.

1. Определяется по экспериментальным данным для ω₁(φ_i) и ω₂(φ_i) в таблице (4) угол φ₀, при котором |ω₁(φ₀)-ω₂(φ₀)|→min.

2. Для этого φ₀ определяем

по данным таблицы (4), (где использовались формулы (2), (11) и (14)). Номер итерации i полагается равным нулю (i=0).

3. По формуле (17) определяется J(φ₀).

4. Это значение подставляется в правую часть итерационной формулы (9) вместо J(φ_i), где все остальные переменные уже известны (определены для φ₀) как результаты измерения или расчетов и хранятся в таблице (4). По формуле (9) определяется величина J(φ₁). Получено первое значение приведенного момента инерции.

5. Найденное значение J(φ₁) подставляется в правую часть выражения (9), а все остальные значения переменных в правой части берутся из таблицы (4) экспериментальных данных теперь для φ=φ₁ Вычисляется значение J(φ₂) и т.д.

На Фиг.2 приведена рассчитанная таким образом функция переменного момента инерции механизма, показанного на Фиг.1. В данном случае N=240. Для наглядности на график выведены значения J(φ) для 24 равноотстоящих положений кривошипа и, следовательно, цена одного деления по оси φ составляет 360°/24=15°.

Источники информации

1. Артоболевский И.И. Теория механизмов и машин. М.: Наука, 1988, 639 с.

2. Киселев М.И., Козлов А.П., Морозов А.Н., Назолин А.А., Пронякин В.И., Соловьев А.В. Измерение периода вращения валопровода турбоагрегата фотоэлектрическим методом // Измерит. Техника. 1996. №12. С.28-29.

3. Гельфонд А.О. Исчисление конечных разностей. М.: Гостехиздат, 1959.

Способ определения приведенного момента инерции механизма, заключающийся в изменении инерционных свойств механизма путем присоединения дополнительного маховика с известным моментом инерции J₀ и измерении угловой скорости звена приведения, отличающийся тем, что дополнительно измеряют угол поворота φ звена приведения и определяют изменение углового ускорения Δε звена приведения, вызванное присоединением пробной массы, а приведенный момент инерции определяют как функцию угла поворота звена приведения из решения численным методом дифференциального уравнения с начальным условием где ω₁ и ω₂ - измеренные угловые скорости,Δε - изменение углового ускорения кривошипа,а угол φ₀ выбирается таким, при котором измеренные угловые скорости ω₁(φ₀) и ω₂(φ₀) максимально совпадают между собой, т.е.