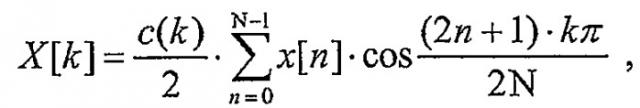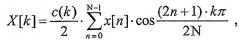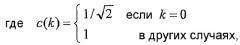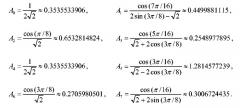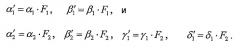Структура преобразования с масштабированными и немасштабированными интерфейсами

Структура преобразования с масштабированными и немасштабированными интерфейсами

Иллюстрации

Показать все

Реферат

Настоящая заявка притязает на приоритет Предварительной заявки (США) серийный номер 60/787562, озаглавленной "CONVERGENCE OF SCALED AND NON-SCALED IDCT ARCHITECTURES", зарегистрированной 29 марта 2006 года, назначенной правопреемнику этой заявки и содержащейся в данном документе по ссылке.

Уровень техники

Область техники, к которой относится изобретение

Настоящее изобретение, в общем, относится к обработке, а более конкретно, к методикам выполнения преобразования данных.

Уровень техники

Преобразования, в общем, используются для того, чтобы преобразовывать данные из одной области в другую область. Например, дискретное косинусное преобразование (DCT), в общем, используется для того, чтобы преобразовывать данные из пространственной области в частотную область, а обратное дискретное косинусное преобразование (IDCT), в общем, используется для того, чтобы преобразовывать данные из частотной области в пространственную область. DCT широко используется для сжатия изображений/видео, чтобы пространственно декоррелировать блоки элементов изображений (пикселов) в изображениях или видеокадрах. Результирующие коэффициенты преобразования в типичном варианте гораздо меньше зависят друг от друга, что делает эти коэффициенты более подходящими для квантования и кодирования. DCT также использует свойство энергетического сжатия, которое является способностью сопоставлять большую часть энергии блока пикселов только с несколькими (в типичном варианте младшего порядка) коэффициентами преобразования. Это свойство энергетического сжатия позволяет упростить проектирование алгоритмов кодирования.

Преобразования, такие как DCT и IDCT, могут быть использованы для различных вариантов применения, которые могут поддерживать различные стандарты кодирования изображений и видео. Следовательно, желательно предоставить интерфейсы, которые могут принимать и предоставлять данные в форматах, подходящих для этих вариантов применения. Более того, поскольку преобразования могут выполняться с большим объемом данных, желательно выполнять преобразования максимально эффективно.

Сущность изобретения

Методики эффективного выполнения полных и масштабированных преобразований с данными, принимаемыми посредством полных и масштабированных интерфейсов, соответственно, описываются в данном документе. Полное преобразование - это преобразование, которое реализует полное математическое описание преобразования. Полное преобразование оперирует с или предоставляет коэффициенты полного преобразования (или просто коэффициенты преобразования). Полное преобразование также может упоминаться как немасштабированное преобразование, законченное преобразование и т.д. Масштабированное преобразование - это преобразование, которое оперирует с или предоставляет коэффициенты масштабированного преобразования, которые являются масштабированными версиями коэффициентов полного преобразования. Масштабированное преобразование может иметь меньшую вычислительную сложность и может быть использовано вариантами применения, которые могут принимать коэффициенты масштабированного преобразования. Полное преобразование может быть использовано вариантами применения, которые хотят обмениваться полными коэффициентами преобразования. Полные и масштабированные преобразования могут быть для двумерного (2D) IDCT, которое может быть реализовано разделимым способом с одномерными (1D) IDCT. Полные и масштабированные преобразования могут также быть для 2D DCT, которое может быть реализовано разделимым способом с преобразованиями 1D DCT. Преобразования 1D IDCT и преобразования 1D DCT могут быть реализованы вычислительно эффективным способом, как описано ниже.

Далее более подробно описаны различные аспекты и признаки изобретения.

Краткое описание чертежей

Фиг.1A иллюстрирует разделимое полное 2D IDCT с 2D масштабированием.

Фиг.1B иллюстрирует разделимое полное 2D IDCT со строково-столбцовым масштабированием.

Фиг.1B иллюстрирует разделимое полное 2D IDCT с 1D масштабированием.

Фиг.1D иллюстрирует разделимое масштабированное 2D IDCT.

Фиг.2 иллюстрирует блок-схему факторизации 8-точечного 1D IDCT.

Фиг.3A иллюстрирует разделимое полное 2D DCT с 2D масштабированием.

Фиг.3B иллюстрирует разделимое полное 2D DCT со строково-столбцовым масштабированием.

Фиг.3B иллюстрирует разделимое полное 2D DCT с 1D масштабированием.

Фиг.3D иллюстрирует разделимое масштабированное 2D DCT.

Фиг.4 иллюстрирует блок-схему факторизации 8-точечного 1D DCT.

Фиг.5 иллюстрирует IDCT-процессор, поддерживающий полный и масштабированный интерфейсы.

Фиг.6 иллюстрирует DCT-процессор, поддерживающий полный и масштабированный интерфейсы.

Фиг.7 иллюстрирует процесс выполнения преобразования.

Фиг.8 иллюстрирует систему кодирования и систему декодирования.

Фиг.9 иллюстрирует блок-схему системы кодирования.

Фиг.10 иллюстрирует блок-схему системы декодирования.

Подробное описание изобретения

Методики, описанные в данном документе, могут быть использованы для различных типов преобразования, таких как DCT, IDCT, дискретное преобразование Фурье (DFT), обратное DFT (IDFT), модулированное перекрывающееся преобразование (MLT), обратное MLT, модулированное комплексное перекрывающееся преобразование (MCLT), обратное MCLT и т.д. Методики также могут быть использованы для различных вариантов применения, таких как обработка изображений, видео и аудио, связь, сети данных, хранение данных, графики и т.д. В общем, методики могут быть использованы для любого варианта применения, который использует преобразование. Для понятности, методики описаны ниже для DCT и IDCT, которые, как правило, используются в обработке изображений и видео.

N-точечное 1D DCT и N-точечное 1D IDCT типа II может быть задано следующим образом:

уравнение (1)

уравнение (2)

x[n] - это функция 1D пространственной области, а X[k] - это функция 1D частотной области.

1D DCT в уравнении (1) оперирует с N входными выборками или значениями пространственной области от x[0] до x[N-1] и формирует N коэффициентов преобразования от X[0] до X[N-1]. 1D IDCT в уравнении (2) оперирует с N коэффициентами преобразования и формирует N выходных выборок. DCT типа II - это один тип преобразования, и он, в общем, считается одним из наиболее эффективных преобразований из различных преобразований с энергетическим сжатием, часто предлагаемых для сжатия изображений/видео.

1D DCT и 1D IDCT могут быть реализованы в своих исходных формах, показанных в уравнениях (1) и (2), соответственно. Тем не менее, существенное снижение вычислительной сложности может быть реализовано посредством нахождения факторизаций, которые приводят к наименьшему возможному числу умножений и сложений, как описано ниже.

1D DCT в уравнении (1) может быть выражено в матричной форме следующим образом:

x = T y , уравнение (3)

где y - это вектор Nx1 входных выборок,

T - это матрица NxN полного 1D DCT, и

x - это вектор Nx1 коэффициентов преобразования.

y содержит входные выборки от x[0] до x[N-1], а x содержит коэффициенты преобразования от X[0] до X[N-1]. Элементы T могут быть получены на основе уравнения (1).

1D DCT может быть факторизовано в произведение матриц следующим образом:

T = S T _S, уравнение (4)

где S = diag (A ₀ ,..., A _N-1 ) - это диагональная матрица множителей масштабирования, а T _S - это матрица NxN масштабированного 1D DCT.

Уравнения (3) и (4) указывают то, что полное 1D DCT может выполняться для y посредством выполнения сначала масштабированного 1D DCT для y и последующего масштабирования результатов с помощью S .

Преимущество декомпозиции полного преобразования в масштабированное преобразование и операцию масштабирования, к примеру, как показано в уравнении (4), заключается в том, что посредством надлежащего выбора множителей масштабирования мультипликативная сложность масштабированного преобразования может быть уменьшена. Например, хорошо известное разложение Arai, Agui и Nakajima (AAN) в "A Fast DCT-SQ Scheme for Images", Transactions of the IEICE, November 1988, формирует масштабированное 8-точечное DCT, которое может быть реализовано только с помощью пяти умножений на иррациональные множители. В отличие от этого, наилучшее известное полное 8-точечное DCT требует 11 таких умножений.

NxN 2D DCT может быть задано следующим образом:

T T = ( S T _S) ( S T _S) = ( S S )( T _S T _S), уравнение (5)

где T T - это кронекеровское произведение T с собой и является матрицей полного 2D DCT, - это матрица масштабированного 2D DCT, а - это матрица множителей масштабирования для масштабированного 2D DCT.

Результат операции в уравнении (5) - это матрица NxN 2D DCT.

2D DCT может выполняться для матрицы N×N входных выборок Y разделимым способом, для одной размерности за раз. Например, 1D DCT может выполняться для каждой строки Y , чтобы получить промежуточную матрицу, и 1D DCT затем может быть выполнено для каждого столбца промежуточной матрицы. Альтернативно, 1D DCT может выполняться для каждого столбца Y , после чего выполняется 1D DCT для каждой строки промежуточной матрицы.

Уравнение (5) указывает то, что 2D DCT может выполняться для Y посредством выполнения сначала 2D DCT для Y , а затем масштабирования результатов. Уравнение (5) также указывает то, что масштабирование для строковых и столбцовых 1D DCT может объединяться в один этап (который является матричным произведением S S ), применяемым к результатам масштабированного 2D DCT.

1D IDCT в уравнении (2) может быть выражено в матричной форме следующим образом:

T ^-1 = T ^t = T ^t _S S , уравнение (6)

где T ^t - это матрица N×N полного 1D IDCT, и "^t" означает транспонирование.

2D IDCT может выражаться следующим образом:

( T T )^-1 = T ^-1 T ^-1 = ( T ^t _S S )( T ^t _S S ) = ( T ^t _S T ^t _S)( S S ) уравнение (7)

Уравнение (7) указывает то, что 2D IDCT может выполняться для матрицы N×N коэффициентов преобразования X посредством масштабирования сначала коэффициентов преобразования и последующего выполнения масштабированного 2D IDCT по масштабированным коэффициентам преобразования. Уравнение (7) также указывает то, что масштабирование для строковых и столбцовых 1D IDCT может объединяться в один этап, предшествующий масштабированному 2D IDCT.

Масштабированная архитектура - это структура, которая использует масштабированное преобразование, а полная архитектура - это структура, которая использует полное преобразование. Масштабированная архитектура может иметь меньшую мультипликативную сложность, чем полная архитектура. Например, масштабированная архитектура может выполнять масштабированное 2D IDCT ( T ^t _S T ^t _S) разделимым строково-столбцовым способом и может использовать 8-точечное масштабированное ID IDCT T _S из разложения AAN для каждой строки и каждого столбца. Мультипликативная сложность этой масштабированной архитектуры может быть 8·8+16·5=64+80=144, или 64 умножения для масштабирования и 5 умножений для каждой из 8 строк и 8 столбцов. В определенных ситуациях масштабирование может быть комбинировано с квантованием, и при этом мультипликативная сложность масштабированной архитектуры может быть уменьшена до примерно 80 умножений. Полная архитектура может выполнять 2D IDCT ( T T ) строково-столбцовым способом и может использовать наилучшее известное полное 8-точечное ID IDCT T для каждой строки и каждого столбца. Мультипликативная сложность этой полной архитектуры может составлять 16·11=176, или 11 для каждой из 8 строк и 8 столбцов. Для разделимой реализации масштабированная архитектура может иметь меньшую мультипликативную сложность, чем полная архитектура.

Масштабированная архитектура может использоваться в структурах, которые предпочитают низкую сложность. Масштабированная архитектура может быть преимущественной, когда имеется только несколько коэффициентов преобразования, чтобы масштабировать, что часто может иметь место для 2D IDCT в декодере изображений/видео. Масштабированная архитектура также может быть преимущественной в структурах, которые предоставляют возможность масштабирования коэффициентов преобразования, которые должны быть комбинированы с квантованием и/или обратным квантованием в кодере/декодере (кодеке) изображений/видео, к примеру, как показано на фиг.8.

Полная архитектура может быть желательной в структурах, которые предпочитают простоту использования. Например, многие вычислительные окружения и приложения могут поддерживать несколько стандартов кодирования изображений и видео. В этих случаях может быть более удобным иметь механизм преобразования, который реализует полное преобразование, и предоставлять гибкий интерфейс ввода/вывода, чтобы дать возможность использования механизма преобразования с различными квантователями и кодеками. Полная архитектура может предоставлять простой интерфейс и может быть более подходящей в таких окружениях.

Структура преобразования, которая может гибко поддерживать различные варианты применения посредством масштабированного и полного интерфейса, описана в данном документе. Структура преобразования может принимать полные входные значения посредством полного интерфейса, выполнять полное преобразование для этих входных значений и предоставлять полные выходные значения, аналогично полной архитектуре. Структура преобразования также может принимать масштабированные входные значения через масштабированный интерфейс, выполнять масштабированное преобразование для этих входных значений и предоставлять масштабированные выходные значения, аналогично масштабированной архитектуре. Структура преобразования внутренне может реализовывать разделимое масштабированное преобразование, чтобы потенциально достигать меньшей сложности и/или повышенной точности. Структура преобразования тем самым может достигать меньшей сложности для определенных вариантов применения, предоставлять простоту применения для других вариантов применения или предоставлять и меньшую сложность, и простоту применения в определенных случаях. Структура преобразования может быть использована как для прямых преобразований (к примеру, DCT), так и для обратных преобразований (к примеру, IDCT). Для простоты структура преобразования конкретно описана ниже для IDCT.

Архитектуры масштабированного и немасштабированного/полного 2D IDCT могут быть выражены следующим образом:

масштабированное 2D IDCT: T ^-1 T ^-1 = ( T ^t _S T ^t _S)( S S ), уравнение (8)

немасштабированное 2D IDCT: T ^-1 T ^-1 = ( T ^t _S S )( T ^t _S S ) уравнение (9)

Полный/немасштабированный интерфейс может принимать коэффициенты преобразования. Полное 2D IDCT может выполняться для этих коэффициентов преобразования следующим образом:

Y = Θ( X )≈ T ^t X T , уравнение (10)

где X - это матрица коэффициентов преобразования,

Θ (.) - это аппроксимация полного 2D IDCT, а

Y - это матрица выходных выборок.

Операторная запись (.) в уравнении (10) используется для того, чтобы указывать то, что аппроксимации с фиксированной запятой могут не основываться исключительно на линейных операциях.

Полное 2D IDCT может осуществляться посредством выполнения полного 1D IDCT для каждой строки и каждого столбца X следующим образом:

θ( x _i) ≈ T ^t x _i, уравнение (11)

где x _i - это i-я строка или столбец X , и

θ (.) - это аппроксимация полного 1D IDCT.

θ (.) может быть использована для строково-столбцовой реализации 2D оператора Θ(.).

Масштабированный интерфейс может принимать коэффициенты масштабированного преобразования, которые могут получаться следующим образом:

X _S = Σ ( X ) ≈ S ^t X S , уравнение (12)

где Σ(.) - это аппроксимация операции 2D масштабирования, а X _S - это матрица коэффициентов масштабированного преобразования.

Масштабированное 2D IDCT может выполняться для коэффициентов масштабированного преобразования следующим образом:

уравнение (13)

где Ξ(.) - это аппроксимация масштабированного 2D IDCT.

Масштабированное 2D IDCT может осуществляться посредством выполнения масштабированного 1D IDCT для каждой строки и каждого столбца X _s следующим образом:

уравнение (14)

где x _S,i - это i-я строка или столбец X _s, и

ξ (.) - это аппроксимация масштабированного 1D IDCT.

ξ(.) может быть использована для строково-столбцовой реализации 2D оператора Ξ(.).

Как показано в уравнении (13), масштабированный интерфейс может быть реализован посредством реализации 2D оператора Ξ(.). Как показано в уравнениях (12) и (13), полный интерфейс может быть реализован посредством реализации оператора 2D масштабирования Σ(.) помимо 2D оператора Ξ(.). Полное 2D IDCT затем может выполняться следующим образом:

уравнение (15)

Уравнение (15) указывает то, что полное 2D IDCT может выполняться для коэффициентов полного преобразования X посредством сначала масштабирования этих коэффициентов преобразования с помощью оператора 2D масштабирования Σ(.) и последующего выполнения 2D IDCT для масштабированных преобразованных коэффициентов с помощью 2D оператора Ξ(.). 2D оператор Ξ(.), в свою очередь, может быть реализован посредством строково-столбцового каскада 1D операторов ξ(.).

2D оператор Θ(.) для разделимого полного 2D IDCT тем самым может быть реализован с помощью 2D оператора Ξ(.) для разделимого масштабированного 2D IDCT и оператора 2D масштабирования Σ(.). 2D масштабирование может быть реализовано различными способами, как описано ниже. Результирующая сложность и производительность разделимого полного 2D IDCT, реализованного с помощью разделимого масштабированного 2D IDCT и 2D масштабирования может быть сравнима с собственным реализованным 2D IDCT.

Фиг.1A иллюстрирует структуру разделимого полного 2D IDCT 100 с 2D масштабированием. 2D IDCT 100 содержит стадию 112 2D масштабирования, за которой следует стадия 114 1D IDCT для строк (или столбцов), за которой дополнительно следует стадия 116 масштабированного 1D IDCT для столбцов (или строк), и завершается стадией 118 выходного форматирования. Стадия 112 2D масштабирования принимает блок NxN коэффициентов преобразования X и может умножать каждый коэффициент преобразования X _ij на множитель масштабирования A _ij и дополнительно сдвигать каждый коэффициент масштабированного преобразования на P битов влево, где P обозначает число зарезервированных битов "мантиссы". После масштабирования величина C=2 ^P-1 может быть добавлена в коэффициент DC-преобразования, чтобы добиться надлежащего округления выходных выборок. Чтобы повысить точность масштабирования, S=P+R битов могут быть использованы при преобразовании множителей масштабирования в целые числа, и надлежащие сдвиги на R битов могут быть выполнены после умножения. S может быть любым надлежащим значением, которое может упрощать реализации на аппаратных платформах, к примеру, S может быть равно 15 или 16 для платформ с 16-битовых множителей без знака.

Стадия 114 IDCT выполняет N-точечное масштабированное 1D IDCT для каждой строки блока коэффициентов масштабированного преобразования из стадии 112 2D масштабирования. Стадия 112 IDCT выполняет N-точечное масштабированное 1D IDCT для каждого столбца промежуточного блока, сформированного посредством стадии 114 IDCT. Масштабированные 1D IDCT для стадий 114 и 116 могут оперировать непосредственно со своими входными данными без выполнения какого-либо внутреннего пре- или пост-масштабирования. После того как все строки и столбцы масштабированы, стадия 118 выходного форматирования может сдвигать результирующие величины из стадии 116 IDCT на P битов вправо, чтобы сформировать блок NxN выходных выборок Y для полного 2D IDCT. Множители масштабирования и константа точности P могут выбираться таким образом, что полное 2D IDCT может быть реализовано с помощью регистров требуемой ширины.

2D масштабирование на стадии 112 может быть выражено следующим образом:

уравнение (16)

где X _ij - это коэффициент преобразования в i-й строке и j-том столбце X , A _i и A _j - это i-й и j-й диагональные элементы, соответственно, S , X _S,ij - это коэффициент масштабированного преобразования в i-й строке и j-м столбце X _s, а ">>R" обозначает операцию сдвига вправо со знаком на R битов. R - это константа, обеспечивающая P битов добавленной точности с фиксированной запятой в коэффициентах масштабированного преобразования X _S,ij.

Таблица может сохранять множители масштабирования A _ij =A _i A _j , для i = 0,..., N-1 и j = 0,..., N-1. Каждый элемент X может быть умножен на соответствующий множитель масштабирования в таблице. До N·N умножений может быть выполнено для N·N элементов X .

Фиг.1B иллюстрирует структуру разделимого полного 2D IDCT 102 с разделимым строково-столбцовым масштабированием. 2D IDCT 102 содержит стадию 122 разделимого строкового-столбцового масштабирования, за которой следует стадия 124 масштабированного 1D IDCT для строк (или столбцов), за которой дополнительно следует стадия 126 масштабированного 1D IDCT для столбцов (или строк), и завершается стадией 128 выходного форматирования. Стадия 122 принимает блок NxN коэффициентов преобразования X и может умножать каждый коэффициент преобразования X_ij в каждой строке i на множитель масштабирования A_i, и затем умножать каждый результирующий коэффициент в каждом столбце j на множитель масштабирования A_j, чтобы получить коэффициенты масштабированного преобразования, следующим образом:

уравнение (17)

Стадия 122 масштабирования тем самым может выполнять 2D масштабирование разделимым способом для строк, за которыми следуют столбцы (или столбцов, за которыми следуют строки). Разделимое строково-столбцовое масштабирование может давать возможность одному и тому же оборудованию быть использованным для масштабирования строк и масштабирования столбцов, что позволяет уменьшать сложность реализации. До 2-N-N умножений может быть выполнено для N·N элементов X . Тем не менее, фактическое число умножений может быть гораздо меньше 2-N-N, поскольку некоторые из множителей масштабирования от A ₀ до A _N-1 могут иметь тривиальные значения (к примеру, 256), и умножение на эти тривиальные множители масштабирования может быть реализовано с помощью простых операций сдвига. Стадии 124, 126 и 128 могут работать таким же образом, что и стадии 114, 116 и 118, соответственно, на фиг.1A.

Фиг.1C иллюстрирует структуру разделимого полного 2D IDCT 104 с масштабированием перед каждым масштабированным 1D IDCT. 2D IDCT 104 содержит масштабированное 1D IDCT со стадией 134 масштабирования для строк (или столбцов), за которой следует масштабированное 1D IDCT со стадией 136 масштабирования для столбцов (или строк), и завершается стадией 138. Стадия 134 IDCT выполняет масштабирование до N-точечного масштабированного 1D IDCT для каждой строки блока коэффициентов преобразования. Стадия 136 IDCT выполняет масштабирование до N-точечного масштабированного 1D IDCT для каждого столбца промежуточного блока, сформированного посредством стадии 134 DCT. Стадии 134 и 136, по сути, выполняют полные 1D IDCT с помощью масштабированных 1D IDCT. Множители масштабирования от A ₀ до A _N-1 и постоянные множители в масштабированном 1D IDCT могут выбираться так, чтобы снижать сложность и/или повышать точность полного 1D IDCT, как описано ниже. Стадия 138 может работать таким же образом, что и стадия 118 на фиг.1A.

Фиг.1D иллюстрирует структуру разделимого масштабированного 2D IDCT 106. 2D IDCT 106 содержит стадию 144 масштабированного 1D IDCT для строк (или столбцов), за которой следует стадия 146 масштабированного 1D IDCT для столбцов (или строк), и завершается стадией 148 выходного масштабирования. Стадия 144 IDCT выполняет N-точечное масштабированное 1D IDCT для каждой строки блока NxN коэффициентов масштабированного преобразования X _s. Стадия 146 IDCT выполняет N-точечное масштабированное 1D IDCT для каждого столбца промежуточного блока, сформированного посредством стадии 144 IDCT. Стадия 148 может работать таким же образом, что и стадия 118 на фиг.1A.

Как проиллюстрировано на фиг.1A-1C, масштабирование для полного 2D IDCT может осуществляться различными способами, например, с помощью 2D масштабирования перед строково-столбцовыми 1D IDCT на фиг. 1A, с помощью строкового-столбцового масштабирования перед строково-столбцовыми 1D IDCT на фиг.1B или с помощью масштабирования перед каждым 1D IDCT на фиг.1C. Масштабирование также может осуществляться другими способами. Как показано на фиг.1D, масштабированное 2D IDCT может выполняться посредством простого пропуска масштабирования и выполнения преобразований 1D IDCT для строк и столбцов.

Различные типы масштабированного 1D IDCT могут быть использованы для строково-столбцовых 1D IDCT на фиг.1A-1D. Например, масштабированное 1D IDCT на основе разложения AAN может быть использовано. Другое масштабированное IDCT с возможно меньшей сложностью описано ниже.

Фиг.2 иллюстрирует блок-схему 200 примерной факторизации 8-точечного 1D IDCT. На блок-схеме 200 каждое сложение представляется символом "", а каждое умножение представляется прямоугольником. Каждое сложение суммирует или вычитает два входных значения и предоставляет выходное значение. Каждое умножение умножает входное значение на постоянный множитель в прямоугольнике и предоставляет выходное значение. Факторизация на фиг.2 имеет умножения на следующие постоянные множители:

α ₁ = α ₂ = 1,Уравнение (18)

β ₁ = β ₂ = C _π/4 = cos(π/4) ≈ 0,707106781,

γ ₁ = C _3π/8 = cos(3π/8) ≈ 0,382683432 и

δ ₁ = S _3π/8 = sin(3π/8) ≈ 0,923879533.

Блок-схема 200 может принимать восемь коэффициентов преобразования от X[0] до X[7] и масштабировать эти коэффициенты преобразования с помощью множителей масштабирования от A ₀ до A ₇, чтобы получить восемь масштабированных коэффициентов преобразования от A ₀ X[0] до A ₇ X[7]. Альтернативно, блок-схема 200 может напрямую принимать восемь коэффициентов масштабированного преобразования. В любом случае, блок-схема 200 выполняет 8-точечное 1D IDCT для восьми коэффициентов масштабированного преобразования и формирует восемь выходных выборок от x[0] до x[7]. Множители масштабирования от A ₀ до A ₇ следующие:

Блок-схема 200 включает в себя ряд операций бабочки. Операция бабочки принимает два входных значения и формирует два выходных значения, где одно выходное значение - это сумма двух входных значений, а другое выходное значение - это разность двух входных значений. Например, операция бабочки для входных значений A ₀ X[0] и A ₄ X[4] формирует выходное значение A ₀ X[0] + A ₄ X[4] для верхней ветви и выходное значение A ₀ X[0] - A ₄ X[4] для нижней ветви.

Факторизация, показанная на фиг.2, приводит всего к 6 умножениям и 28 сложениям, что значительно меньше числа умножений и сложений, требуемых для прямых расчетов по уравнению (2). Умножения выполняются с иррациональными константами, представляющими синус и косинус различных углов, которые являются кратными π/8 для 8-точечного ID IDCT. Иррациональная константа - это константа, которая не является соотношением двух целых чисел. Умножения на иррациональные константы могут эффективно выполняться в целочисленной арифметике с фиксированной запятой, когда иррациональная константа аппроксимируется посредством двоично-рациональной константы. Двоично-рациональная константа - это константа с двоичным знаменателем, и она имеет форму c/2 ^b, где b и c - это целые числа, и b>0.

Умножение целочисленной переменной x на иррациональную константу μ в целочисленной арифметике с фиксированной запятой может выполняться посредством аппроксимации иррациональной константы с помощью двоично-рациональной константы следующим образом:

μ ≈ c / 2^b , уравнение (19)

где μ - это иррациональная константа, которая должна быть аппроксимирована, а c/2 ^b - это двоично-рациональная константа.

При условии целочисленной переменной x и двоично-рациональной константы u = c/2 ^b целочисленное произведение

y = (x · c) / 2^b , уравнение (20)

может быть аппроксимировано с помощью последовательности промежуточных значений

x ₀, x ₁, x ₂, …, x _t, уравнение (21)

где x₀=0, x ₁ =x, и для всех 2 ≤ i ≤ t значений x _i получается следующим образом:

x _i = ±x _j ± x _k · 2^Si, с j, k<i, уравнение (22)

где x _k 2 ^Si подразумевает сдвиг влево или вправо (в зависимости от знака константы s _i ) промежуточного значения x _k на |s _i| битов.

В уравнении (22) x _i может быть равно x _j + x _k · 2 ^Si, x _j - x _k · 2 ^Si или - x _j + x _k · 2 ^Si. Каждое промежуточное значение x _i в последовательности может быть извлечено на основе двух предыдущих промежуточных значений x _j и x _k в последовательности, где x _j или x _k может быть равно нулю. Каждое промежуточное значение x _i может быть получено с одним сдвигом и/или одним сложением. Сдвиг не требуется, если s _i равно нулю. Сложение не требуется, если x _j=x ₀ =0.

Общее число сложений и сдвигов для умножения определяется посредством числа промежуточных значений в последовательности, которое равно t, а также выражения, используемого для каждого промежуточного значения. Умножение на двоично-рациональную константу u, по сути, разворачивается в последовательность операций сдвига и сложения. Последовательности задаются таким образом, что конечное значение в последовательности становится требуемым целочисленным произведением, или:

x _t ≈ y, уравнение (23)

Умножение целочисленной переменной x на две иррациональные константы μ и η в целочисленной арифметике с фиксированной запятой может выполняться посредством аппроксимации иррациональных констант с помощью двоично-рациональной константы следующим образом:

μ ≈ c / 2^b и η ≈ e / 2^d , уравнение (24)

где c/2 ^b и e/2 ^d - это две двоично-рациональные константы, а b, c, d и e - это целые числа, при b>0 и d>0.

При условии целочисленной переменной x и двоично-рациональных констант u = c/2 ^b и v = e/2 ^d целочисленные произведения

y = (x · c) / 2^b и z = (x · e) / 2^d, уравнение (25)

могут быть аппроксимированы с помощью последовательности промежуточных значений

x ₀, x ₁, x ₂, …, x _t, уравнение (26)

где x₀=0, x ₁ =x, и для всех 2 ≤ i ≤ t значений x _i получается следующим образом:

x _i = ±x _j ± x _k · 2^Si, с j, k<i, уравнение (27)

Последовательность задается таким образом, чтобы требуемые целочисленные произведения получались на этапах m и n следующим образом:

x _m ≈ y и x _n ≈ z, уравнение (28)

где m, n≤ t и либо m, либо n не равно t.

Как показано в уравнениях (24)-(28), умножение целочисленной переменной на x на иррациональные константы μ и η может быть аппроксимировано с помощью общей последовательности промежуточных значений, сформированных посредством операций сдвига и сложения и с помощью промежуточных результатов, чтобы уменьшить общее число операций.

В описанных выше вычислениях тривиальные операции, такие как сложения и вычитания нулей и сдвиги на нуль битов, могут быть опущены. Могут быть сделаны следующие упрощения:

x _i = ±x ₀ ± x _k · 2^Si => x _i = ± x _k · 2^Si, уравнение (29)

x _i = ±x _i ± x _k · 2⁰ => x _i = ±x _i ± x _k. уравнение (30)

В уравнении (29) выражение слева от "=>" влечет за собой сложение или вычитание нуля (обозначенного как x₀) и может выполняться с помощью одного сдвига, как показано посредством выражения справа от "=>". В уравнении (30) выражение слева от "=>" влечет за собой сдвиг на нуль битов (обозначенный как 2⁰) и может выполняться с помощью одного сложения, как показано посредством выражения справа от "=>". Уравнения (29) и (30) могут быть применены к уравнениям (22) и (27) при вычислении x _i.

Чтобы уменьшить вычисления, первый общий множитель F₁ может быть применен к постоянным множителям α₁ и β₁ на блок-схеме 200, а второй общий множитель F₂ может быть применен к постоянным множителям α₂, β₂, β₁ и γ₁ следующим образом:

уравнение (31)

Множители масштабирования A ₀ и A ₇ также могут быть масштабированы так, чтобы учитывать общие множители F ₁ и F ₂ следующим образом:

уравнение (32)

Различные комбинации значений для общих множителей F ₁ и F ₂ могут быть оценены. Для каждой комбинации значений F ₁ и F ₂ общее число логических и арифметических операций для 1D IDCT и точность выходных выборок может быть оценена.

Таблица 1 показывает примерную аппроксимацию с фиксированной запятой для 1D IDCT на фиг.2 при F ₁ =2523/2048 и F ₂ =2607/2048. В таблице 1 множители масштабирования от A' ₀ до A' ₇ и масштабированные общие множители приведены в первом столбце. Каждый множитель может быть аппроксимирован с помощью двоично-рациональной константы, приведенной во втором столбце. Последовательность промежуточных значений для умножения переменой x на одну или две двоично-рациональные константы приведена в третьем столбце. Число операций сло