Способ и устройство для декодирования кода с генераторной матрицей низкой плотности

Способ и устройство для декодирования кода с генераторной матрицей низкой плотности

Иллюстрации

Показать все

Реферат

Область техники

Изобретение касается кодирования и декодирования данных и, в частности, способа и устройства для декодирования кода с генераторной матрицей низкой плотности.

Уровень техники

В процессе передачи данных, если принятый пакет данных в результате проверки в приемнике оказывается ошибочным, то ошибочный сегмент данных отбрасывают, что эквивалентно его стиранию. Эту модель канала называют каналом со стиранием, и она является важной моделью канала. При передаче по Интернету файл передают на основе пакетов данных. Обычно каждый пакет данных будет или безошибочно принят приемником, или не будет принят приемником вообще. В протоколе TCP (Transmission Control Protocol, протокол управления передачей) способом борьбы с потерей пакетов в сети является обнаружение ошибок и механизм повторной передачи, то есть канал обратной связи от передатчика к приемнику используется для того, чтобы управлять пакетами данных, которые должны передаваться повторно. Когда приемник обнаруживает потерю пакетных данных, он генерирует управляющий сигнал повторной передачи до корректного получения целого пакета данных; а когда приемник получает пакет данных, он также генерирует сигнал подтверждения приема. Передатчик может также отслеживать каждый пакет данных до получения сигнала подтверждения приема по обратной связи, а иначе он передает его повторно.

Широковещательная служба передачи данных, основанная на потоковой модели и модели загрузки файла, является службой типа "точка - много точек", в которой не разрешена обратная связь, так что традиционный механизм повторной передачи при обнаружении ошибок неприменим, и используется прямое исправление ошибок (FEC, Forward Error Correction), чтобы обеспечить достоверную передачу данных. Классическое прямое исправление ошибок прикладного уровня включает коды Рида-Соломона (RS), цифровые фонтанные коды и так далее. Поскольку кодирование и декодирование для кода Рида-Соломона имеют более высокую сложность, код Рида-Соломона обычно пригоден для ситуаций, в которых длина кода мала. Код с преобразованием Лаби (LT, Luby Transform) и код Raptor являются двумя практическими применимыми цифровыми фонтанными кодами. Коду LT присуще линейное время кодирования и декодирования, что представляет собой существенное улучшение по сравнению с кодом Рида-Соломона, в то время как у кода Raptor более высока эффективность декодирования, поскольку код Raptor использует технику предварительного кодирования. И служба мультимедийной широковещательной/многоадресной передачи (MBMS, Multimedia Broadcast/Multicast Service), и цифровое телевидение (DVB, Digital Video Broadcasting) проекта партнерства 3-го поколения (3GPP, 3rd Generation Partnership Project) принимают код Raptor компании Digital Fountain как схему кодирования для обеспечения FEC.

Если первые K битов кодированного кодового слова совпадают с битами информации, то такой код называют систематическим кодом. Процесс кодирования является процессом формирования N битов длины кода в соответствии с K битами информации и добавлением N-K битов четности, чтобы обеспечить обнаружение ошибок и исправление ошибок. Код LT не поддерживает подход кодирования с использованием систематического кода и, таким образом, код LT не может удовлетворить некоторым практическим требованиям к кодированию с FEC. Код Raptor поддерживает систематический код; однако код Raptor нуждается в отдельном процессе предварительного кодирования, то есть нуждается в одной матрице предварительного кодирования, и, таким образом, сложность кодирования будет более высокая.

Из-за недостатков вышеупомянутых способов кодирования был предложен код с генераторной матрицей низкой плотности (LDGC, Low Density Generator matrix Code). Код LDGC относится к типу линейных блочных кодов, а ненулевые элементы в его генераторной матрице (матрице кодирования) обычно разреженные. Кроме того, код LDGC является также систематическим кодом.

При кодировании кодом LDGC формируется промежуточная переменная согласно соответствующей связи между битами информации (то есть, данными, которые будут переданы) систематического кода и этой промежуточной переменной, и затем генераторную матрицу умножают на промежуточную переменную, чтобы получить кодированное кодовое слово. В частности, в процессе кодирования необходимо, во-первых, добавить d=L-K известных битов заполнения к K битам информационной последовательности m, чтобы сформировать последовательность s из L битов и затем, согласно уравнениям I×G_ldgc(0:L-1, 0:L-1)=s решить уравнения, чтобы сформировать последовательность I промежуточной переменной из L битов, затем умножить генераторную матрицу на промежуточную переменную, то есть I×G_ldgc(0:L-1, 0:N+d-1), сформировать N+d битов (включая α битов заполнения) последовательности кодовых слов , при этом d битов заполнения в не требуется передавать, таким образом действительно передают последовательность кодовых слов из N битов. После того как проходит через канал (где возможно происходит стирание), принятой последовательностью кодовых слов в приемнике является последовательность R. При этом s является вектором размером 1×L, I является вектором размером 1×L, R является вектором размером 1×N и G_ldgc (0:L-1, 0:L-1) является квадратной матрицей размером L×L, которая обычно является нижней треугольной матрицей или верхней треугольной матрицей, а G_ldgc (0:L-1, 0:N+d-1) является матрицей размером L×(N+d). Детально процесс кодирования описан в патенте "Способ и устройство для кодирования кодом с генераторной матрицей низкой плотности, а также способ и устройство для декодирования".

Процесс декодирования кода LDGC должен, во-первых, использовать принятую последовательность кодовых слов R (включая биты заполнения; также все следующие указанные принятые последовательности кодовых слов включают биты заполнения), генераторную матрицу G_ldgc кода LDGC и уравнения соотношения I×G_ldgc(0:L-1, 0:N+d-1)=R для промежуточной переменной I, чтобы решить уравнения, вывести промежуточную переменную I и затем вывести биты информации s согласно отношению I×G_ldgc(L-1, 0:L-1)=s между битами информации s (включая биты заполнения) и промежуточной переменной I и избавиться от битов заполнения, чтобы получить исходную информационную последовательность m.

При этом самым важным шагом является получение промежуточной переменной, что обычно требует решения множества линейных уравнений. В инженерной практике для решения линейных уравнений можно использовать способ гауссова исключения или итеративный способ и т.п. В соответствии с особенностями LDGC способ гауссова исключения более пригоден для декодирования LDGC. Таким образом, скорость процесса гауссова исключения прямо влияет на скорость декодирования LDGC.

В соответствии с необходимостью описания способа гауссова исключения любой "вектор" или "матрица" с нижним индексом t в нижнем регистре в следующем описании относится к транспонированию исходного вектора или матрицы. Если содержимое вектора или матрицы полностью совпадает с его транспонированным содержимым, иногда они могут относиться к тому же самому объекту. Например, G_ldgct является результатом транспонирования G_ldgc, I_t является результатом транспонирования I и R_t является результатом транспонирования R. Поскольку I и R являются векторами-строками, I_t и R_t являются векторами-столбцами.

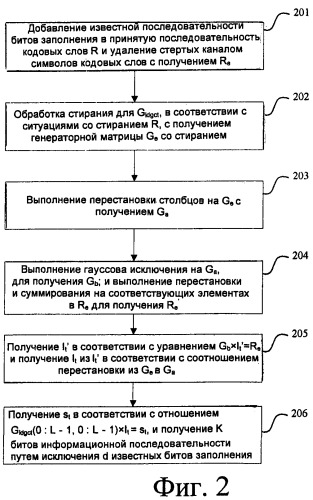
Фиг.1 является схемой транспонированной генераторной матрицы G_ldgct кода LDGC. Как показано на фиг.1, квадратная матрица, соответствующая первым L строкам в G_ldgct, обычно является верхней треугольной матрицей или нижней треугольной матрицей. При этом элементы x и y на фиг.1 могут быть равны 0.

В процессе определения промежуточной переменной I_t в соответствии с линейными уравнениями G_ldgct(0:N+d-1, 0:L-1)×I_t=R_t, при выполнении гауссова исключения требуется выполнить три вида элементарных преобразований "перестановка строк, суммирование строк и перестановка столбцов" в отношении матрицы G_ldgct. Согласно теории линейной алгебры, чтобы гарантировать правильность уравнений, одновременно с обработкой матрицы G_ldgct посредством элементарных преобразований, I_t и R_t должны быть соответственно обработаны следующим образом:

1) перестановка строк, если i-я строка и j-я строка в G_ldgct переставлены местами, то i-й бит и j-й бит в R_t должны быть переставлены местами;

2) суммирование строк, если i-я строка и j-я строка в G_ldgct сложены вместе, то i-й бит и j-й бит в R_t должны быть сложены вместе (сложение по модулю 2);

3) перестановка столбцов, если i-й столбец и j-й столбец в G_ldgct переставлены местами, то i-й бит и j-й бит в I_t должны быть переставлены местами.

Окончательный результат состоит в том, чтобы получить I_t, однако элементы в I_t были соответственно переставлены при выполнении перестановки столбцов в G_ldgct, и, таким образом, перестановки в I_t должны быть записаны для выполнения последующего обратного процесса перестановки. В инженерной практике для того, чтобы записать перестановки, сделанные в I_t, может использоваться матрица. Поскольку вектор R_t не представляет собой конечные необходимые данные, он может быть обработан непосредственно, без необходимости записи ситуации с его обработкой.

Поскольку эти соотношения преобразования строго соответствуют друг другу, и сложность гауссова исключения, главным образом, заключается в обработке G_ldgct, для удобства описания все элементарные преобразования для G_ldgct и соответствующая обработка для I_t и R_t выполняются строго в соответствии с вышеупомянутыми тремя преобразованиями. С целью выделения важных моментов последующее описание обработки для I_t и R_t может быть таким образом упрощено.

Согласно известному уровню техники декодирование LDGC с использованием обычного способа гауссова исключения имеет два недостатка: первое, обычный способ не лучшим образом использует ту особенность, что генераторная матрица LDGC является строго верхней треугольной или нижней треугольной (как показано на фиг.1) для упрощения операции исключения; второе, обычный способ не может использовать особенность структуры генераторной матрицы LDGC, чтобы прямо формировать индексы ненулевых элементов матрицы, и требует хранения целой генераторной матрицы, что увеличивает сложность хранения и вычисления. Таким образом, эффективность декодирования с использованием обычного способа гауссова исключения довольно низкая.

Сущность изобретения

Техническая проблема, решаемая данным изобретением, состоит в том, чтобы создать высокоэффективный способ декодирования LDGC, преодолевающий недостатки предшествующего уровня техники.

Чтобы решить вышеупомянутую проблему, данное изобретение предлагает способ декодирования кодов с генераторной матрицей низкой плотности (LDGC) для декодирования принятой битовой информационной последовательности, переданной после ее кодирования кодом LDGC, включающий:

S1: добавление L-K известных битов заполнения в принятую последовательность R кодовых слов, удаление стертых в канале символов кодовых слов из последовательности R, чтобы получить R_e; и удаление строк, соответствующих стертым в канале символам кодовых слов, из матрицы G_ldgct, полученной транспонированием генераторной матрицы LDGC, чтобы получить матрицу G_e;

S2: выполнение перестановки столбцов матрицы G_e так, чтобы сформировать матрицу , где А - нижняя треугольная квадратная матрица порядка М, и запись перестановки столбцов, соответствующей отношению между G_e и G_a;

S3: выполнение гауссова исключения на матрице G_a, чтобы сформировать матрицу G_b, в которой первые L строк составляют единичную матрицу; и одновременно выполнение операций перестановки и суммирования на соответствующих элементах матрицы R_e в соответствии с операциями перестановки строк и суммирования строк в гауссовом исключении, чтобы сформировать ;

S4: получение согласно соотношению и выполнение обратной перестановки на матрице в соответствии с соответствующим соотношением перестановки столбцов, чтобы получить I_t; и

S5: получение s_t согласно отношению G_ldgct(0:L-1, 0:L-1)×I_t=s_t и удаление L-K известных битов заполнения из s_t, чтобы получить K битов информационной последовательности;

где G_ldgct является матрицей из N+L-K строк и L столбцов.

Кроме того, М=L-X_L, a X_L является числом стертых в канале битов в первых L символах кодовых слов последовательности R.

Кроме того, Xset_L сконфигурирован так, чтобы быть набором индексов стертых символов кодовых слов в первых L символах кодовых слов последовательности R с d известными битами заполнения, и число индексов набора равно X_L, и

на шаге S2 столбцы матрицы G_e, индексы которых принадлежат Xset_L, перемещают в наиболее правую сторону G_e, а последовательными столбцами, индексы которых не принадлежат Xset_L, заполняют освобожденные позиции соответствующих столбцов, чтобы получить матрицу G_a.

Кроме того, на шаге S3 выполнение гауссова исключения на матрице G_a включает следующие подшаги:

S31: выполнение гауссова исключения на А и D в матрице G_a, чтобы преобразовать А в единичную матрицу E_M порядка М, и одновременно преобразовать D в матрицу, все элементы которой являются нулями, имеющую (N-K-(X_T-X_L)) строк и М столбцов, то есть

;

S32: выполнение гауссова исключения на B-DA^-1C в , чтобы сделать единичной матрицей квадратную матрицу, соответствующую первым L-M строкам, и выполнение исключения, чтобы сделать А^-1С матрицей, все элементы которой являются нулями, имеющей М строк и L-M столбцов, то есть

.

Кроме того, на шаге S31 применяют следующий способ определения, является ли элемент Н[x, y] в строке x и столбце y в А и D ненулевым элементом или нет, и гауссово исключение выполняют на А и D в соответствии с позициями ненулевых элементов:

S311: позиции строки и столбца x' и y' указанного элемента Н[x,y] в G_ldgct получают в соответствии с набором Xset индексов удаленных символов кодовых слов в последовательности R, которая заполнена d известными битами заполнения;

S312: если , то Н[x,y] является нулевым элементом, и эта последовательность операций заканчивается, а иначе выполняют следующий шаг;

S313: если ix_z=mod (iy_z+offset, z), то H[x,y] является ненулевым элементом, а иначе Н[x,y] является нулевым элементом;

где z является коэффициентом расширения, z_max является максимальным коэффициентом расширения;

x_z=floor(x'/z), y_z=floor(y'/z);

ix_z=mod(x',z), iy_z=mod(y',z); и

.

Данное изобретение также предлагает устройство для декодирования кодов с генераторной матрицей низкой плотности (LDGC) для декодирования принятой битовой информационной последовательности, переданной после кодирования кодом LDGC, при этом устройство включает: блок заполнения и обработки стирания, блок перестановки столбцов, блок гауссова исключения и блок генератора информационной последовательности, причем

блок заполнения и обработки стирания используется для добавления d известных битов заполнения в принятую последовательность R кодовых слов и удаления стертых каналом символов кодовых слов для формирования и вывода R_e; а также удаления строк, соответствующих стертым каналом символам кодовых слов, из матрицы G_ldgct, полученной транспонированием генераторной матрицы LDGC, для формирования и вывода G_e;

блок перестановки столбцов используется для выполнения перестановки столбцов в матрице G_e, выведенной из блока заполнения и обработки стирания, с получением матрицы и для вывода матрицы G_a, где А - нижняя треугольная матрица порядка М, а также для вывода информации о перестановке столбцов, соответствующей информации об отношении G_e и G_a;

блок гауссова исключения используется для выполнения гауссова исключения на матрице G_a, выведенной из блока перестановки столбцов, для формирования и вывода матрицы G_b, первые L строк которой образуют единичную матрицу; и одновременно для выполнения операций перестановки и суммирования на соответствующих элементах R_e с выхода блока заполнения и обработки стирания, в соответствии с операциями перестановки строк и суммирования строк в процессе гауссова исключения, для формирования и вывода ;

блок генератора информационной последовательности используется для формирования в соответствии с выражением ; выполнения обратной перестановки на с формированием I_t в соответствии с соответствующим соотношением перестановки столбцов, выведенным из блока перестановки столбцов; формирования s_t в соответствии с выражением G_ldgct(0:L-1, 0:L-1)×I_t=s_t и вывода К битов информационной последовательности после удаления d известных битов из s_t;

где G_ldgct является матрицей из N+L-K строк и L столбцов.

Кроме того, указанная матрица А, сформированная перестановкой столбцов, выполняемой блоком перестановки столбцов, является треугольной квадратной матрицей порядка М, M=L-X_L, a X_L является числом стертых в канале битов в первых L символах кодовых слов последовательности R.

Кроме того, полагая, что Xset_L является набором индексов стертых символов кодовых слов в первых L символах кодовых слов последовательности R, заполненной упомянутыми d известными битами, и число индексов набора является упомянутым X_L,

блок перестановки столбцов перемещает в матрице G_e столбцы, индексы которых принадлежат Xset_L, в наиболее правую сторону матрицы G_e, и поочередно заполняет последовательными столбцами, индексы которых не принадлежат Xset_L, освобожденные позиции соответствующих столбцов, чтобы получить матрицу G_a.

Кроме того, блок гауссова исключения использует следующие подшаги, чтобы выполнить гауссово исключение:

S31: выполнение гауссова исключения на А и D в матрице G_a, чтобы преобразовать А в единичную матрицу E_M порядка М, и одновременно преобразовать D в матрицу, все элементы которой являются нулями, имеющую (N-K-(X_T-X_L)) строк и М столбцов, то есть

;

S32: выполнение гауссова исключения на B-DA^-1C в , чтобы сделать первые L-M строк единичной матрицей, и выполнение исключения, чтобы сделать А^-1С матрицей, все элементы которой являются нулями, имеющей М строк и L-M столбцов, то есть

.

Кроме того, блок гауссова исключения использует следующий способ определения, является ли элемент Н[x,y] в строке x и столбце y в А и D ненулевым элементом, и выполняет гауссово исключение на А и D в соответствии с позициями ненулевых элементов:

S311: позиции строки и столбца x' и y' указанного элемента Н[x,y] в G_ldgct получают в соответствии с набором Xset индексов удаленных символов кодовых слов в последовательности R, которая заполнена d известными битами;

S312: если , то Н[x,y] является нулевым элементом, и эта последовательность операций заканчивается, а иначе выполняется следующий шаг;

S313: если ix_z=mod(iy_z+offset, z), то Н[x,y] является ненулевым элементом, а иначе Н[x,y] является нулевым элементом;

где z является коэффициентом расширения, z_max является максимальным коэффициентом расширения;

x_z=floor(x'/z), y_z=floor(y'/z);

ix_z=mod(x',z), iy_z=mod(y',z); и

.

Использование способа декодирования согласно данному изобретению позволяет лучше использовать свойство диагонализации структурной матрицы кодирования LDGC. По сравнению со способом декодирования, в котором прямо применяется способ гауссова исключения, способ декодирования согласно данному изобретению может значительно уменьшить сложность декодирования и значительно увеличить скорость декодирования, что позволяет использовать LDGC в высокоскоростных системах связи.

Краткое описание чертежей

Фиг.1 является схемой транспонированной генераторной матрицы G_ldgct кода LDGC.

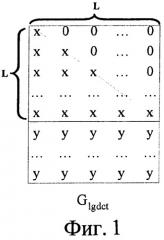
Фиг.2 является блок-схемой способа декодирования кода с генераторной матрицей низкой плотности согласно варианту осуществления данного изобретения.

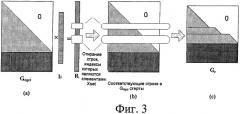
Фиг.3 является схемой обработки стирания для генераторной матрицы согласно ситуациям стирания для принятой последовательности кодовых слов R.

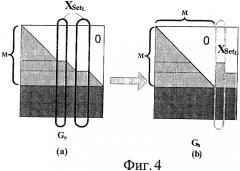
Фиг.4 является схемой перестановки столбцов для генераторной матрицы стирания G_e согласно варианту осуществления данного изобретения.

Фиг.5 является схемой выполнения гауссова исключения на G_a согласно варианту осуществления данного изобретения.

Фиг.6 является блок-схемой способа оценки нулевых элементов согласно варианту осуществления данного изобретения.

Фиг.7 является схемой устройства для декодирования кода с генераторной матрицей низкой плотности согласно варианту осуществления данного изобретения.

Предпочтительные варианты осуществления изобретения

С целью удобства описания, предположим, что X_T символов кодовых слов в принятой последовательности R кодовых слов (включающей биты заполнения) длиной N+d все вместе стерты каналом. Набором индексов позиций этих X_T стертых символов кодовых слов является Xset. В частности, все элементы, индексы позиций которых в Xset меньше чем L, образуют набор Xset_L. Число элементов набора Xset_L равно X_L, то есть Xset_L означает, что X_L символов кодовых слов стерты каналом в первых L символах в последовательности R кодовых слов. Положим также, что М=L-X_L.

Поскольку основные элементы во всех объектах при декодировании LDGC принадлежат конечному полю Галуа GF(2), то все вычисления между объектами являются вычислениями, определенными конечным полем GF(2).

Основная идея данного изобретения состоит в том, чтобы использовать особенность диагонализации структурной генераторной матрицы LDGC, во-первых, чтобы выполнить перестановку столбцов в генераторной матрице LDGC со стиранием, что делает генераторную матрицу LDGC имеющей форму , где матрица А является квадратной матрицей порядка М и является строго нижней треугольной матрицей, а затем выполнить упрощенное декодирование, используя то, что А является строго нижней треугольной матрицей, и А и D имеют структурную особенность.

Данное изобретение ниже будет описано подробно вместе с чертежами и вариантами его осуществления.

Фиг.2 является блок-схемой способа декодирования кода с генераторной матрицей низкой плотности согласно варианту осуществления данного изобретения. Как показано на фиг.2, этот способ включает следующие шаги:

201: заполнение известной последовательностью битов длиной d=L-K соответствующих позиций в принятой последовательности кодовых слов R, например: 1, 1, …, 1, и, тем временем, удаление стертых каналом символов кодовых слов и получение матрицы R_e.

Здесь K является длиной исходных битов информации, а L является длиной кода после того, как исходные биты информации дополнены заполнением.

202: в соответствии с ситуациями со стиранием принятой последовательности R кодовых слов выполняют стирание (удаление) строк в генераторной матрице LDGC G_ldgct и получают генераторную матрицу G_e со стиранием.

Фиг.3 является схемой обработки стирания для генераторной матрицы в соответствии с ситуациями стирания для принятой последовательности кодовых слов R. Как показано на фиг.3, первые L строк генераторной матрицы G_e со стиранием больше не являются нижней треугольной квадратной матрицей.

Предположим, что X_T символов {r_i, r_j, …, r_p…r_x} в R (r₀,r₁, …r_N+d-1), заполненной известной битовой последовательностью, стерты каналом, где X_L символов {r_i, r_j,…, r_p} в первых L символах стерты каналом; тогда Xset={i, j, …, p, …, x}; Xset_L={i, j, …p}. Соответственно строки с номерами {i, j, …, p, …, x} в G_ldgct стерты, чтобы получить G_e. В это время, поскольку несколько строк в верхней матрице G_e стерты, G_e больше не строго диагональная матрица, как это показано на фиг.3(с).

203: выполнение на генераторной матрице G_e со стиранием такой перестановки столбцов, которая делает квадратную матрицу порядка М с вершиной в (0, 0) нижней треугольной матрицей. После перестановки матрица G_e обозначена как генераторная матрица G_a с перестановкой. Одновременно выполняется запись соответствующего отношения перестановки столбцов G_e и G_a, которая используется для последующей операции перестановки на матрице I_t, чтобы сформировать матрицу .

Фиг.4 является схемой перестановки столбцов для генераторной матрицы G_e со стиранием.

В частности, чтобы получить нижнюю треугольную матрицу, переместим в матрице G_e столбцы, номера которых принадлежат набору Xset_L в самое правое положение в G_e, а освобожденные позиции в соответствующих столбцах заполним последовательными столбцами, номера которых не принадлежат Xset_L, и получим генераторную матрицу с перестановкой:

.

При этом матрица А является квадратной матрицей порядка М и является строго нижней треугольной матрицей; матрица С является матрицей размера M×(L-М); матрица D является матрицей размера (N-K-(X_T-X_L))×M; и матрица В является матрицей размера (N-K-(X_T-X_L)×(L-М).

В соответствии с ситуациями с перестановкой столбцов в G_ldgct одновременно соответственно делают перестановку в I_t. Предположим, что I_t после перестановки будет , и отношение перестановки между I_t и может быть записано в виде матрицы, которая используется для последующей обработки в виде обратной перестановки.

204: выполнение гауссова исключения на генераторной матрице G_a с перестановкой, что делает квадратную матрицу порядка L, составленную из первых L строк G_a, единичной матрицей порядка L (если G_a имеет полный ранг). Матрица, подвергнутая исключению, обозначена как G_b, то есть ; одновременно выполняют перестановку и суммирование на соответствующих элементах в R_e и полагают, что R_e преобразована в .

Вышеуказанное обозначение E_L относится к единичной матрице порядка L.

Поскольку у G_a есть следующие особенности:

1) все диагональные строки А имеют ненулевые элементы, и А - строго нижняя треугольная матрица;

2) ненулевые элементы в А и D могут быть непосредственно вычислены с использованием уравнения, заданного при построении генераторной матрицы при кодировании. Таким образом, А и D фактически не требуется сохранять.

Таким образом, процесс гауссова исключения для G_a может быть рассмотрен как включающий следующие три подпроцесса:

204а) гауссово исключение выполняют, используя свойства А: А преобразуют в единичную матрицу Е_м порядка М;

Когда гауссово исключение выполняют на А, позиция каждого ненулевого элемента в А может быть вычислена непосредственно, и операция суммирования на А выполняется в соответствии с позициями ненулевых элементов. Таким образом, матрицу А фактически не требуется сохранять.

Конкретный способ вычисления позиции каждого ненулевого элемента в А (или способ определения, является ли каждый элемент в А нулем или нет) подробно описан ниже.

Посредством выполнения гауссова исключения (операция суммирования строк) на матрице А, А преобразуется в единичную матрицу Е_м порядка М. Вышеупомянутая операция суммирования строк будет одновременно выполняться на матрице С. Окончательный результат эквивалентен тому, что А и С одновременно умножены на А^-1 слева, то есть:

204b) гауссово исключение выполняют на матрице D с использованием единичной матрицы Е_м и D преобразуют в матрицу со всеми нулевыми элементами. Соответственно из В следует вычесть результат умножения А^-1С слева на D, здесь вычитание элементов между матрицами эквивалентно сложению элементов между матрицами по модулю 2. Окончательный результат эквивалентен следующему:

Точно так же, когда гауссово исключение выполняют на D, позиция каждого ненулевого элемента в D может быть вычислена непосредственно, и операция суммирования выполняется на D в соответствии с позицией каждого ненулевого элемента. Таким образом, матрицу D не требуется сохранять фактически. Определенный способ вычисления позиции каждого ненулевого элемента в D (или способ определения, является ли каждый элемент в D нулем или нет) описан подробно ниже.

Вышеупомянутый процесс показан на фиг.5(а) и фиг.5(b).

Чтобы упростить описание, предположим, что S=B-DA^-1С.

204с) выполняют гауссово исключение на S.

Если G_a имеет полный ранг, матрица S может быть преобразована гауссовым исключением в матрицу, включающую единичную матрицу порядка (L-М) (то есть матрица, соответствующая первым L-M строкам, является единичной матрицей), и верхний А^-1С может быть устранен полностью. То есть матрица G_a может быть окончательно преобразована гауссовым исключением к следующей форме:

Первые L-M строк вышеупомянутой матрицы составляют единичную матрицу порядка (L-M), а все последние строки являются нулевыми строками, как это показано на фиг.5(с).

Если у G_a нет полного ранга, то декодирование завершается неудачей, и этот способ заканчивается.

Точно так же, в соответствии с операциями перестановки строк и суммирования строк в гауссовом исключении на матрице G_a, выполняются операции перестановки и суммирования на соответствующих элементах R_e, и полагается, что R_e преобразуется в .

205: в соответствии с уравнениями может быть получено уравнение . Согласно этому уравнению может быть получено непосредственно, и затем I_t может быть получено из путем выполнения обратной перестановки в соответствии с соотношением перестановки между I_t и (то есть соотношением перестановки столбцов при преобразовании из G_e в G_a).

206: в соответствии с соотношением G_ldgct(0:L-1, 0:L-1)×I_t=s_t между битами информации s (включая биты заполнения) и промежуточной переменной I, получение битов информации s_t и получение информационной последовательности длиной K битов путем исключения d известных битов заполнения.

Ниже в качестве примера возьмем А, чтобы описать способ определения, является ли каждый элемент в А и D ненулевым элементом или нет. Это определение для элементов в D является таким же, как и для А.

Фиг.6 является блок-схемой способа определения нулевых элементов согласно варианту осуществления данного изобретения.

Прежде всего опишем каждое обозначение, используемое в способе определения:

- основная матрица LDGC, определенная в стандарте СММВ; размер составляет k_b×n_b=12×40, а размер транспонированной основной матрицы составляет n_b×k_b=40×12.

Коэффициент расширения составляет z=ceil(L/k_b); где функция ceil(•) означает округление до ближайшего большего целого значения.

Максимальный коэффициент расширения составляет z_max=683.

Как показано на фиг.6, этот способ использует следующие шаги, чтобы определить, является ли А[x,y] нулем или нет:

601: в соответствии с индексами удаленных строк Xset, получение позиций строк и столбцов x' и y' элемента А[x,y] в матрице G_ldgct перед процессом стирания; то есть А[x, y] является элементом в строке x и в столбце y в матрице G_ldgct;

602: вычисление x_z=floor(x'/z) и y_z=floor(y'/z);

Функция floor(•) означает округление до ближайшего целого в меньшую сторону.

603: определение, является ли элемент А[x,y] нулем или нет, в соответствии с тем, является ли нулем элемент в строке x_z и столбце y_z в , то есть :

если , то А[x,y]=0;

если , то А[x,y]=0 может быть ненулевым, и должна быть выполнена следующая операция определения.

604: вычисление ix_z=mod(x',z) и iy_z=mod(y',z);

605: вычисление смещения "offset" согласно модифицированной формуле, определенной по стандарту СММВ.

Модифицированная формула является следующей: , где равно , или ;

и смещение равно .

606: в соответствии с тем, равно ли ix_z величине mod(iy_z+offset, z) или нет, судят, является ли А[x,y] нулем или нет:

если ix_z=mod(iy_z+offset, z), то А[x,y] - это ненулевой элемент;

иначе А[x,y] - нулевой элемент.

Способ определения, является ли элемент D[x,y] в D нулевым элементом или нет, совпадает с вышеописанными шагами.

Фиг.7 является схемой устройства для декодирования кода с генераторной матрицей низкой плотности согласно варианту осуществления данного изобретения. Как показано на фиг.7, это устройство включает блок заполнения и обработки стирания, блок перестановки столбцов, блок гауссова исключения и блок генератора информационной последовательности. При этом,

блок заполнения и обработки стирания используется для добавления d известных битов заполнения в принятую последовательность кодовых слов R и для удаления стертых каналом символов кодовых слов для формирования и вывода R_e; а также для удаления строк, соответствующих вышеупомянутым стертым каналом символам кодовых слов, в транспонированной матрице G_ldgct генераторной матрицы LDGC для формирования и вывода матрицы G_e;

блок перестановки столбцов используется для того, чтобы выполнить перестановку столбцов в матрице G_e, выведенной из блока заполнения и обработки стирания, с получением квадратной матрицы А порядка М, вершиной которой является элемент в строке 0 и столбце 0 в G_e, которая является нижней треугольной матрицей, а также используется для формирования и вывода , и вывода информации о перестановке столбцов, соответствующей информации о соотношении G_e и G_a;

M=L-X_L, где X_L - число битов, стертых