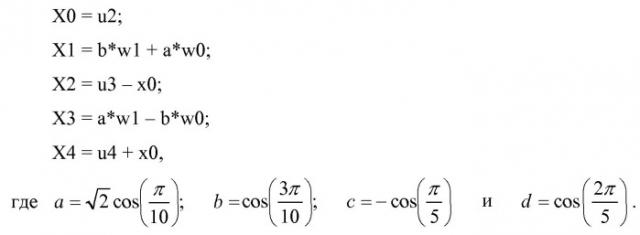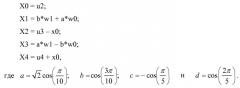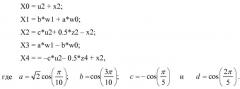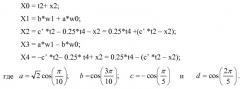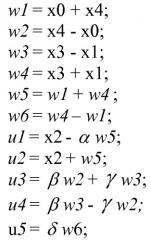Быстрые алгоритмы для вычисления 5-точечного dct-ii, dct-iv и dst-iv, и архитектуры

Быстрые алгоритмы для вычисления 5-точечного dct-ii, dct-iv и dst-iv, и архитектуры

Иллюстрации

Показать все

Реферат

Уровень техники

Испрашивание приоритета по §119 раздела 35 Кодекса законов США

Настоящая заявка на патент испрашивает приоритет предварительной заявки США № 61/013579, озаглавленной «Fast Algorithms for Computation of 5-Point DCT-II, DCT-IV, and DST-V, and Architecture for Design of Transforms of Size N=5*2^K», поданной 13 декабря 2007 г., предварительной заявки США № 61/016106, озаглавленной «Fast Algorithms for Computation of 5-point DCT-II, DCT-IV, and DST-IV, and Architecture for Design of Transforms of sizes N=5*2k», поданной 21 декабря 2007 г., и предварительной заявки США № 61/039194, озаглавленной «G.EV-VBR MDCT Module», поданной 25 марта 2008 г., обе переданы правопреемнику настоящей заявки и таким образом в явной форме включены в настоящий документ по ссылке.

Область техники, к которой относится изобретение

Нижеследующее описание, в основном, относится к кодерам и декодерам и, в частности, к эффективной реализации MDCT/IMDCT для речевых и аудиокодеков.

Уровень техники

Одной целью аудиокодирования является сжатие аудиосигнала до требуемого ограниченного количества информации, в то же время сохраняя насколько возможно исходное качество звука. В процессе кодирования аудиосигнал во временной области преобразуется в частотную область, и соответствующий процесс декодирования осуществляет такую обратную операцию.

В качестве части такого процесса кодирования сигнал может обрабатываться модифицированным дискретным косинусным преобразованием (MDCT). Модифицированное дискретное косинусное преобразование (MDCT) представляет собой преобразование, относящееся к анализу Фурье, основанное на дискретном косинусном преобразовании типа IV (DCT-IV), с дополнительным свойством, что блоки перекрываются, так что окончание одного блока совпадает с началом следующего блока. Это перекрытие способствует тому, чтобы избегать паразитных артефактов, и, в дополнение к свойствам уплотнения энергии дискретного косинусного преобразования (DCT), делает MDCT особенно привлекательным для применений сжатия сигнала.

Вокодеры работают с частотами дискретизации входного сигнала или 8 кГц, или 16 кГц, и с кадрами 10 или 20 миллисекунд. Следовательно, их банки фильтров MDCT представляют собой или 160-, или 320-точечные преобразования.

Однако, если будущие речевые кодеры будут поддерживать функциональную возможность переключения блоков, также может потребоваться поддержка прореженных размеров (например, 160, 80, 40 точек). Следовательно, эффективные реализации преобразований малых размеров желательны для реализации большего преобразования, использующего базовое преобразование малого размера.

Сущность изобретения

Нижеследующее представляет упрощенное изложение сущности одного или нескольких вариантов осуществления, чтобы обеспечить базовое понимание некоторых вариантов осуществления. Это изложение сущности не является исчерпывающим обзором всех рассматриваемых вариантов осуществления и не предназначено, чтобы определять ключевые или критические элементы всех вариантов осуществления, или определять объем любого или всех вариантов осуществления. Его единственной целью является представление некоторых принципов одного или нескольких вариантов осуществления в упрощенном виде в качестве вводной части к более подробному описанию, которое представлено ниже.

Способ и/или устройство кодирования обеспечиваются для вычисления значений преобразования. Принимаются входные значения временной области, представляющие аудиосигнал. Входные значения преобразуются в спектральные коэффициенты, используя модифицированное дискретное косинусное преобразование (MDCT), которое рекурсивно прореживается в множество 5-точечных преобразований. Могут быть реализованы многочисленные разложения для эффективной обработки 5-точечного преобразования.

В одном примере (фиг.5) по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа II (DCT-II) (502), раскладываемое на двенадцать (12) операций сложения, восемь (8) операций умножения, и длину наибольшего пути в три (3) операции. Например, по меньшей мере одно из множества 5-точечных преобразований включает в себя по меньшей мере одно дискретное косинусное преобразование типа II (DCT-II) (502), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается по меньшей мере множеством промежуточных результатов:

так что

В другом примере (фиг.6) по меньшей мере одно из множества 5-точечных преобразований включает в себя по меньшей мере одно дискретное косинусное преобразование типа II (DCT-II) (602), раскладываемое на двенадцать (12) операций сложения, пять (5) операций умножения, две (2) операции сдвига, и длину наибольшего пути в четыре (4) операции. Например, по меньшей мере одно из множества 5-точечных преобразований включает в себя по меньшей мере одно дискретное косинусное преобразование типа II (DCT-II) (602), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается по меньшей мере множеством промежуточных результатов:

так что

В другом примере (фиг.7) по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа II (DCT-II) (702), раскладываемое на двенадцать (12) операций сложения, пять (5) операций умножения, одну (1) операцию сдвига, и длину наибольшего пути в четыре (4) операции. Например, по меньшей мере одно из множества 5-точечных преобразований включает в себя по меньшей мере одно дискретное косинусное преобразование типа II (DCT-II) (702), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается тем, что имеет промежуточные результаты:

так что

В другом примере (фиг.8) по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа II (DCT-II) (802), раскладываемое на двенадцать (12) операций сложения, четыре (4) операции умножения, две (2) операции сдвига, и длину наибольшего пути в четыре (4) операции. Например, по меньшей мере одно из множества 5-точечных преобразований включает в себя по меньшей мере одно дискретное косинусное преобразование типа II (DCT-II) (802), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается по меньшей мере множеством промежуточных результатов:

так что

Альтернативно, по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно преобразование (802), раскладываемое на двенадцать (12) операций сложения, пять (5) операций умножения, одну (1) операцию сдвига, и длину наибольшего пути в четыре (4) операции.

В другом примере (фиг.9) по меньшей мере одно из множества 5-точечных преобразований может включать в себя дискретное косинусное преобразование типа IV (DCT-IV) (902), раскладываемое на двадцать (20) операций сложения, шестнадцать (16) операций умножения, и длину наибольшего пути в три (3) операции. Например, по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа IV (DCT-IV) (902), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается по меньшей мере множеством промежуточных результатов:

так что

где

В другом примере (фиг.10) по меньшей мере одно из множества 5-точечных преобразований может включать в себя дискретное косинусное преобразование типа IV (DCT-IV) (1002), раскладываемое на двадцать (20) операций сложения, двенадцать (12) операций умножения, и длину наибольшего пути в четыре (4) операции. Например, по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа IV (DCT-IV) (1002), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается по меньшей мере множеством промежуточных результатов:

так что

где

В другом примере (фиг.14) по меньшей мере одно из множества 5-точечных преобразований может включать в себя дискретное косинусное преобразование типа IV (DCT-IV) (1402), раскладываемое на шестнадцать (16) операций сложения, девять (9) операций умножения, и длину наибольшего пути в пять (5) операций. Например, по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа IV (DCT-IV) (1402), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается по меньшей мере множеством промежуточных результатов:

так что

В другом примере (фиг.15), в котором по меньшей мере одно из множества 5-точечных преобразований может включать в себя дискретное косинусное преобразование типа IV (DCT-IV) (1502), раскладываемое на пятнадцать (15) операций сложения, десять (10) операций умножения, две (2) операции сдвига, и длину наибольшего пути в пять (5) операции. Например, по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа IV (DCT-IV) (1502), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается по меньшей мере множеством промежуточных результатов:

так что

В другом примере (фиг.16) по меньшей мере одно из множества 5-точечных преобразований может включать в себя дискретное косинусное преобразование типа IV (DCT-IV) (1602/1702), раскладываемое на пятнадцать (15) операций сложения, одиннадцать (11) операций умножения, две (2) операции сдвига, и длину наибольшего пути в пять (5) операций. Например, по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа IV (DCT-IV) (1602), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается по меньшей мере множеством промежуточных результатов:

так что

В другом примере (фиг.17) по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа IV (DCT-IV) (1702), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается по меньшей мере множеством промежуточных результатов:

так что

В другом примере (фиг.18) по меньшей мере одно из множества 5-точечных преобразований может включать в себя дискретное косинусное преобразование типа IV (DCT-IV) (1802), раскладываемое на пятнадцать (15) операций сложения, двенадцать (12) операций умножения, две (2) операции сдвига, и длину наибольшего пути в пять (5) операций. Например, по меньшей мере одно из множества 5-точечных преобразований может включать в себя по меньшей мере одно дискретное косинусное преобразование типа IV (DCT-IV) (1802), которое принимает входной вектор [x0, x1, x2, x3, x4] для получения выходного вектора [X0, X1, X2, X3, X4], и отличается промежуточными результатами:

так что

Кроме того, способ и/или устройство преобразования могут выполнять операцию создания окна над входными значениями перед выполнением преобразования, причем операция создания окна реализует функцию асимметричного окна.

В некоторых реализациях MDCT может реализовывать по меньшей мере одно из 640-, 320-, 160-, 80-, 40-точечного преобразования, используя 5-точечное дискретное косинусное преобразование типа II.

В других реализациях MDCT может реализовывать по меньшей мере одно из 640-, 320-, 160-, 80-, 40-точечного преобразования, используя 5-точечное дискретное косинусное преобразование типа IV.

В еще других реализациях MDCT может реализовывать по меньшей мере одно из 640-, 320-, 160-, 80-, 40-точечного преобразования, используя 5-точечное дискретное косинусное преобразование типа II и 5-точечное дискретное косинусное преобразование типа IV.

В еще других реализациях MDCT реализует по меньшей мере одно из 640-, 320-, 160-, 80-, 40-точечного преобразования, используя 5-точечное дискретное синусное преобразование типа IV.

Способ и/или устройство декодирования обеспечиваются для вычисления значений обратного преобразования. Принимаются входные значения спектральных коэффициентов, представляющие аудиосигнал. Входные значения спектральных коэффициентов затем преобразуются в выходные значения временной области, используя обратное модифицированное дискретное косинусное преобразование (IMDCT), которое рекурсивно прореживается на множество 5-точечных обратных преобразований.

В одном примере (фиг.32) по меньшей мере одно из множества 5-точечных обратных преобразований может включать в себя по меньшей мере одно обратное дискретное косинусное преобразование типа II (DCT-II) (3202), раскладываемое на двенадцать (12) операций сложения, четыре (4) операции умножения, две (2) операции сдвига и длину наибольшего пути в четыре (4) операции. Например, по меньшей мере одно из множества 5-точечных обратных преобразований может включать в себя по меньшей мере одно обратное дискретное косинусное преобразование типа II (IDCT-II) (3202), которое принимает входной вектор [X0, X1, X2, X3, X4] для получения выходного вектора [x0, x1, x2, x3, x4], и отличается по меньшей мере множеством промежуточных результатов:

так что

Кроме того, способ и/или устройство преобразования могут выполнять операцию создания окна над входными значениями после выполнения обратного преобразования, причем операция создания окна реализует функцию асимметричного окна.

В одной реализации IMDCT может реализовывать по меньшей мере одно из 640-, 320-, 160-, 80-, 40-точечного преобразования, используя 5-точечное обратное дискретное косинусное преобразование типа II.

В другой реализации IMDCT может реализовывать по меньшей мере одно из 640-, 320-, 160-, 80-, 40-точечного преобразования, используя 5-точечное обратное дискретное косинусное преобразование типа IV.

В еще другой реализации IMDCT может реализовывать по меньшей мере одно из 640-, 320-, 160-, 80-, 40-точечного преобразования, используя 5-точечное обратное дискретное косинусное преобразование типа II и 5-точечное обратное дискретное косинусное преобразование типа IV.

В одной реализации IMDCT может реализовывать по меньшей мере одно из 640-, 320-, 160-, 80-, 40-точечного преобразования, используя 5-точечное обратное дискретное синусное преобразование типа IV.

Краткое описание чертежей

Различные признаки, особенности и преимущества могут стать очевидными из подробного описания, изложенного ниже, при рассмотрении вместе с чертежами, на которых подобные позиции идентифицируют соответствующие элементы по всем чертежам.

Фиг.1 представляет собой блок-схему, иллюстрирующую пример кодера, который может включать в себя банк фильтров анализа MDCT.

Фиг.2 представляет собой блок-схему, иллюстрирующую пример того, как преобразование может быть реализовано меньшими преобразованиями.

Фиг.3 представляет собой блок-схему, иллюстрирующую пример декодера, который может включать в себя банк фильтров синтеза IMDCT.

Фиг.4 представляет собой блок-схему, иллюстрирующую пример того, как обратное преобразование может быть реализовано меньшими обратными преобразованиями.

Фиг.5 представляет собой блок-схему последовательности операций, иллюстрирующую первый пример разложения 5-точечного DCT-II преобразования.

Фиг.6 представляет собой блок-схему последовательности операций, иллюстрирующую второй пример разложения 5-точечного DCT-II преобразования.

Фиг.7 представляет собой блок-схему последовательности операций, иллюстрирующую третий пример разложения 5-точечного DCT-II преобразования.

Фиг.8 представляет собой блок-схему последовательности операций, иллюстрирующую альтернативный пример разложения 5-точечного DCT-II преобразования.

Фиг.9 представляет собой блок-схему последовательности операций, иллюстрирующую первый пример разложения 5-точечного DCT-IV преобразования.

Фиг.10 представляет собой блок-схему последовательности операций, иллюстрирующую второй пример того, как может быть реализовано 5-точечное DCT-IV преобразование.

Фиг.11 представляет собой блок-схему, иллюстрирующую то, как DCT-IV преобразование может отображаться на DCT-II преобразование для преобразования входных коэффициентов в выходные коэффициенты.

Фиг.12 представляет собой блок-схему, иллюстрирующую 5-точечное DCT-IV преобразование, которое может быть реализовано с использованием 5-точечного DCT-II преобразования для преобразования входных коэффициентов в выходные коэффициенты.

Фиг.13 представляет собой блок-схему, иллюстрирующую пример разложения 5-точечного DCT-IV преобразования по фиг.12, которое может быть реализовано с использованием 5-точечного DCT-II преобразования.

Фиг.14 представляет собой блок-схему, иллюстрирующую то, как отображение DCT-IV преобразования на фиг.13 может быть объединено с DCT-II преобразованием по фиг.6.

Фиг.15 представляет собой блок-схему, иллюстрирующую то, как DCT-IV преобразование по фиг.14 может быть дополнительно модифицировано в эквивалентное преобразование.

Фиг.16 представляет собой блок-схему, иллюстрирующую то, как DCT-IV преобразование по фиг.15 может быть дополнительно модифицировано в эквивалентное преобразование.

Фиг.17 представляет собой блок-схему, иллюстрирующую то, как DCT-IV преобразование по фиг.16 может быть дополнительно модифицировано в эквивалентное преобразование.

Фиг.18 представляет собой блок-схему, иллюстрирующую то, как DCT-IV преобразование по фиг.17 может быть дополнительно модифицировано в эквивалентное преобразование.

Фиг.19 представляет собой блок-схему, иллюстрирующую то, как преобразование размера N может рекурсивно разбиваться на меньшие преобразования размера N/2 до тех пор, пока оно не будет представлено множеством 5-точечных преобразований.

Фиг.20 представляет собой блок-схему, иллюстрирующую пример прореживания и разбиения преобразования, при котором 10-точечное DCT-IV преобразование рекурсивно разбивается на множество меньших 5-точечных DCT-II преобразований.

Фиг.21 представляет собой блок-схему, иллюстрирующую то, как обратное преобразование размера N может рекурсивно разбиваться на меньшие обратные преобразования размера N/2 до тех пор, пока оно не будет представляться множеством 5-точечных обратных преобразований.

Фиг.22 представляет собой блок-схему, иллюстрирующую пример прореживания и разбиения обратного преобразования, при котором обратное 10-точечное IDCT-IV преобразование рекурсивно разбивается на множество меньших обратных преобразований 5-точечного IDCT-II.

Фиг.23 иллюстрирует форму асимметричного окна, которая может использоваться для снижения задержки, ассоциированной с этапом преобразования, до 10 мс, в то же время сохраняя такое же количество частотных коэффициентов.

Фиг.24 представляет собой блок-схему, иллюстрирующую устройство для вычисления значений преобразования.

Фиг.25 иллюстрирует пример способа кодирования сигнала, использующего MDCT преобразование, основанное на 5-точечном базовом преобразовании.

Фиг.26 представляет собой блок-схему, иллюстрирующую устройство для вычисления значений преобразования.

Фиг.27 иллюстрирует пример способа декодирования сигнала, использующего IMDCT преобразование, основанное на базовом IDCT-II преобразовании.

Фиг.28 иллюстрирует альтернативный пример прореживания и разбиения преобразования, при котором 10-точечное DCT-IV преобразование рекурсивно разбивается на множество меньших 5-точечных DCT-II преобразований.

Фиг.29 иллюстрирует 10-точечное IDCT-IV преобразование, которое представляет собой преобразование, обратное преобразованию по фиг.28.

Фиг.30 представляет собой блок-схему, иллюстрирующую пример прореживания и разбиения преобразования, при котором обратное 10-точечное DCT-IV преобразование рекурсивно разбивается на множество меньших 5-точечных DCT-II преобразований и 5-точечных DCT-IV.

Фиг.31 представляет собой блок-схему, иллюстрирующую пример обратного преобразования для прямого преобразования по фиг.30.

Фиг.32 иллюстрирует обратное преобразование, соответствующее прямому преобразованию по фиг.8.

Подробное описание

Ниже описываются различные варианты осуществления с ссылкой на чертежи, на которых идентичные позиционные обозначения используются для ссылки на идентичные элементы по всем чертежам. В нижеследующем описании, для целей объяснения, различные специфические детали излагаются для того, чтобы обеспечить полное понимание одного или нескольких вариантов осуществления. Может быть очевидным, однако, что такой вариант(ы) осуществления может быть осуществлен на практике без этих специфических деталей. В других случаях общеизвестные конструкции и устройства показаны в виде блок-схемы, чтобы способствовать описанию одного или нескольких вариантов осуществления.

Обзор

Один признак предусмотрен для осуществления N-точечного MDCT преобразования (где N=5*2∧K, для некоторого целого числа K>=1) посредством отображения его на N/2-точечных DCT-IV, DST-IV и/или DCT-II преобразований меньшего размера. В одном примере MDCT может систематически прореживаться с коэффициентом 2 и использовать масштабированную 5-точечную базовую функцию на последнем этапе. Один признак обеспечивает несколько быстрых алгоритмов для вычисления базовых DCT-II, DCT-IV и DST-IV преобразований с размером пять (5). Общая архитектура преобразования, которая заявляется здесь, представляет собой обобщенный процесс прореживания, рекурсивно разбивающий преобразования размера N на два преобразования размера N/2, где N=5*2∧K, и где окончательные (наименьшие) 5-точечные преобразования реализуются с использованием быстрых методов, описанных в данном документе. Преобразования такого размера возникают в структуре банков фильтров MDCT для применений речевого и аудиокодирования, таких как недавние и новые стандарты G.729.1, G.718 и EVRC-WB (широкополосный усовершенствованный кодек с переменной скоростью).

Другой признак предусмотрен для использования этапа модифицированного создания окна MDCT, который объединяет вышеописанную архитектуру для вычисления MDCT с асимметричным окном для снижения задержки, ассоциированной с этапом преобразования, в то же время сохраняя такое же количество частотных коэффициентов.

Структура кодека

Фиг.1 представляет собой блок-схему, иллюстрирующую пример кодера, который может включать в себя банк фильтров анализа MDCT. Кодер 102 может принимать входной аудиосигнал 104. Банк 106 фильтров анализа MDCT (т.е. модифицированное дискретное косинусное преобразование, основанное на дискретном косинусном преобразовании типа IV) работает для разложения входного аудиосигнала 104 временной области на множество субполосных сигналов и преобразования сигналов в частотную область, где каждый субполосный сигнал преобразуется в коэффициент преобразования на субполосу на блок. Результирующий сигнал затем квантуется квантователем 108 и кодируется статистическим кодером 110 для получения битового потока 112 оцифрованного аудиосигнала. Согласно одному примеру банк 106 фильтров анализа MDCT может быть реализован функцией 114 создания окна, преобразованием 116 (например, временной области в частотную область) и/или функцией 118 масштабирования. Банк 106 фильтров анализа MDCT, включающий в себя функцию 114 создания окна, преобразование 116 и/или функцию 116 масштабирования, может быть реализован аппаратными средствами (например, в виде процессора, схемы, программируемого логического устройства и т.д.), программными средствами (например, инструкциями, исполняемыми процессором) и/или их комбинацией.

Фиг.2 представляет собой блок-схему, иллюстрирующую пример того, как преобразование может быть реализовано посредством меньших преобразований. В данном примере преобразование 116 по фиг.1 может принимать множество входных сигналов 202 и создавать множество выходных сигналов 204. Для выполнения этого преобразование 116 может быть представлено одним или несколькими преобразованиями этого же или меньшего размера. Например, преобразование 116 может быть реализовано множеством k-точечных DCT-IV преобразований 206а и 206b. В свою очередь, каждое k-точечное DCT-IV преобразование 206а и 206b может быть реализовано одним или несколькими n-точечными DCT-II преобразованиями 208а, 208b или 210а, 210b. Отметьте, что в некоторых реализациях могут использоваться дискретные синусные преобразования (DST)-IV вместо DCT-IV преобразований. Посредством рекурсивного разбиения большего преобразования 116 на множество меньших преобразований 208 упрощается реализация большего преобразования 116. Однако желательна реализация эффективного алгоритма меньших преобразований для достижения быстрой производительности преобразования, которая минимизирует операции. В одном примере преобразование 116 может принимать входные значения x(0) … x(m) 202 временной области, представляющие аудиосигнал, и преобразовывать их в спектральные коэффициенты X(0) … X(m) 204 частотной области. Ниже описываются различные реализации этих меньших преобразований.

Фиг.3 представляет собой блок-схему, иллюстрирующую пример декодера, который может включать в себя банк фильтров синтеза IMDCT. Декодер 302 может принимать битовый поток 304. Статистический декодер 306 декодирует битовый поток 304, который затем деквантуется устройством 308 деквантования для получения сигнала частотной области. Банк 310 фильтров синтеза IMDCT (т.е. обратное модифицированное дискретное косинусное преобразование, основанное на дискретном косинусном преобразовании типа IV) работает для преобразования сигнала 304 частотной области обратно в аудиосигнал 312 временной области. Банк 310 фильтров синтеза IMDCT может изменять на обратные операции банка 106 фильтров анализа MDCT. Согласно одному примеру банк 310 фильтров синтеза IMDCT может быть реализован посредством функции 314 масштабирования, обратного преобразования 316 (например, частотной области во временную область) и функции 318 создания окна плюс перекрытия и сложения. Банк 310 фильтров синтеза IMDCT, включающий в себя функцию 314 масштабирования, обратное преобразование 316 и/или функцию 318 создания окна, может быть реализован аппаратными средствами (например, процессором, схемой, программируемым логическим устройством и т.д.), программными средствами (например, инструкциями, исполняемыми процессором) и/или их комбинацией.

Фиг.4 представляет собой блок-схему, иллюстрирующую пример того, как обратное преобразование может быть реализовано меньшими обратными преобразованиями. В данном примере обратное преобразование 316 по фиг.3 может принимать множество входных сигналов 402 и создавать множество выходных сигналов 404. Для выполнения этого обратное преобразование 316 может быть представлено одним или несколькими преобразованиями этого же или меньшего размера. Например, обратное преобразование 316 может быть реализовано множеством обратных k-точечных IDCT-IV преобразований 406а и 406b. В свою очередь, каждое обратное k-точечное IDCT-IV преобразование 406а и 406b может быть реализовано одним или несколькими n-точечными IDCT-II преобразованиями 408а, 408b или 410а, 410b. Отметьте, что в некоторых реализациях могут использоваться обратные дискретные синусные преобразования (IDST)-IV вместо IDCT-IV преобразований. В одном примере преобразование 316 может принимать спектральные коэффициенты X(0) … X(m) 402 частотной области, представляющие аудиосигнал, и преобразовывать их в восстановленные выходные значения x(0) … x(m) 404 временной области. Однако желательна эффективная реализация алгоритма меньших обратных преобразований для достижения быстрых рабочих характеристик преобразования, которые минимизируют операции.

Отметьте, что входные сигналы для преобразований MDCT 102 и IMDCT 302 могут обрабатываться в качестве кадров или блоков, имеющих множество точек данных. Следовательно, чтобы основанный на MDCT вокодер (такой как, например, G.722.1 или G.722.1C) поддерживал блоки данных, имеющие длину кадра, меньшую 320, необходимы преобразования прореженных размеров. Для блоков, имеющих длину кадра 160, 80, 40 и т.д., наблюдается, что эти размеры все являются кратными 5. Поэтому последний неуменьшаемый (посредством методов прореживания) размер блока может использовать преобразование с размером 5. Обращается внимание, что с точки зрения сложности вычислений является более эффективным разработать 5-точечное DCT-II преобразование, чем или DCT-IV преобразование, или быстрое преобразование Фурье (FFT).

Определение преобразований MDCT

Используя матричное представление, MDCT преобразование может быть представлено матрицей М:

Следовательно, и , где x представляет матрицу входных отсчетов , X представляет матрицу результирующих коэффициентов MDCT , и представляет матрицу восстановленных выходных результатов .

Чтобы реализовать преобразование MDCT, оно может отображаться на функцию N/2-точечного базового преобразования. Например, преобразование 116 на фиг.1 может быть реализовано как одно или несколько N/2-точечных DCT-IV преобразований.

DCT-IV преобразование может быть определено как:

В то же время IDCT-IV преобразование может быть определено как:

MDCT преобразование может отображаться на N/2-точечное DCT-IV преобразование как:

и IMDCT преобразование может отображаться на N/2-точечное IDCT-IV преобразование как

где

где I _N/4 представляет собой единичную матрицу размера N/4×N/4, и J _N/4 представляет собой инверсную матрицу порядка размера N/4×N/4, и матрица S определяется как

и представляет собой матрицу DCT-IV размера N/2×N/2, которая может быть определена как

Посредством использования свойств симметрии и инволютивности матрицы DCT-IV, она может отображаться на DCT-II преобразование. DCT-II преобразование может определяться как:

Аналогично, IDCT-II преобразование может определяться как:

где , если k=0, иначе 1.

Определение преобразований DCT-IV, DST-IV и DCT-II

Согласно признаку преобразование 116 (фиг.1) и обратное преобразование 316 (фиг.3) могут прореживаться и реализоваться при помощи одного или нескольких DCT-IV преобразований или DST-IV преобразований (и IDCT-IV или DST-IV), которые могут быть реализованы в виде одного или нескольких DCT-II преобразований (и IDCT-II), соответственно.

DCT-IV и IDCT-IV могут быть определены, соответственно, как:

DST-IV и IDST-IV могут быть определены, соответственно, как:

Аналогично, DCT-II и его обратные преобразования могут быть определены, соответственно, как:

где , если k=0, иначе 1

В уравнениях 1-6 {x(n)}, для n=0,1,…N-1, представляет входную последовательность отсчетов, N обозначает длину кадра, X(k) представляет собой результирующие коэффициенты MDCT.

В случае, когда N=5, матрицы C_IV для DCT-IV преобразования, S_IV для DST-IV преобразования и C_II для DCT-II преобразования могут быть представлены, соответственно, как:

(Матрица А)

(Матрица В)

(Матрица С)

Для упрощения представления DCT-II множители могут игнорироваться, и все коэффициенты могут умножаться на , при использовании следующей системы обозначений:

таким образом получая:

В данном случае отметьте, что a ²+b ²=1,25, и что c ²+d ²=0,75. Кроме того, также отметьте, что c-d=0,5. Это следует из алгебраических выражений для участвующих значений косинуса:

Аналогично, в случае DCT-IV все коэффициенты умножаются на и используют систему обозначений:

получая:

Отметьте, что f²+i ²=2, и аналогично g ²+h ²=2. Кроме того, отметьте, что f+i=×c, и что h+g=×a. Это следует из алгебраических выражений для участвующих значений косинуса:

Наконец, в случае DST-IV все коэффициенты могут умножаться на и используют систему обозначений:

для получения:

Аналогично для случая DCT-IV, отметьте, что в данном случае f²+i ²=2, и аналогично g ²+h ²=2.

Вывод быстрых алгоритмов для вычисления 5-точечного DCT-II

Чтобы достичь эффективности обработки, преобразования самых меньших размеров, используемые большими преобразованиями, должны быть быстрыми и эффективными. Это достигается посредством минимизации операций (например, умножения, сложения и сдвига), выполняемых этими преобразованиями малого размера. Следовательно, для достижения этого могут реализовываться различные разложения для преобразований самого малого размера. Выбор того, какое разложение преобразования реализуется, может зависеть от различных факторов, включая возможности испол