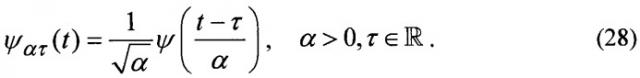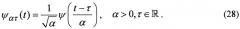Устройство обнаружения шумовых гидроакустических сигналов в виде звукоряда на основе вычисления интегрального вейвлет-спектра

Устройство обнаружения шумовых гидроакустических сигналов в виде звукоряда на основе вычисления интегрального вейвлет-спектра

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области гидроакустики, а именно к устройствам обнаружения шумовых сигналов со спектральной плотностью мощности (СПМ) в виде звукорядов (ЗР) (состоящих из дискретных составляющих (ДС) с кратными центральными частотами) на фоне аддитивной помехи.

Известно, что реализация оптимального приема при решении задачи обнаружения сигналов на фоне помех во многом определяется уровнем знаний о принимаемом сигнале.

Основными источниками шумового сигнала, излучаемого движущимися в воде гидроакустическими объектами (надводными судами или подводными лодками), являются [1-6]:

- энергетическая установка, которая включает машину, редукторы, вал, подшипники и т.д.;

- гребные винты, которые хотя и являются частью энергетической установки, но должны рассматриваться отдельно вследствие существенно отличного способа, которым они создают акустические шумы;

- вспомогательные механизмы, в состав которых входят механические и электрические системы, не относящиеся к энергетической установке (такие как вентиляторы, генераторы, насосы и т.п.);

- гидродинамические эффекты, состоящие в первую очередь из шумов обтекания корпуса корабля или ПЛ, а также шумов различных частей оборудования и конструкций, которые создаются за счет протекания различных жидкостей.

При этом суммарный шум движущегося гидроакустического объекта содержит в своем составе два основных типа шумов, отличающихся по своей сути. Эти отличия проявляются в виде их спектральных характеристик.

Одним из них является широкополосный шум с непрерывным спектром. Под непрерывным подразумевается спектр, уровень которого представляет собой непрерывную функцию СПМ шума в зависимости от частоты G(f). В технической литературе эту составляющую СПМ шума называют «сплошной частью спектра».

Другим типом шума является узкополосный (или тональный) шум, имеющий прерывистый спектр. Этот тип шума состоит из отдельных «тональных» (синусоидальных) составляющих, и его спектр содержит «линейчатые» компоненты, появляющиеся на дискретных частотах. В технической литературе эти синусоидальные компоненты шума называют «дискретными составляющими» (ДС) спектра шума G_ДC(f).

Таким образом, шум, излучаемый движущимся в воде объектом, обычно является смесью шумов двух указанных типов и может рассматриваться как шум с непрерывным спектром, содержащим отдельные наложенные дискретные составляющие [1-6].

Возникновение узкополосных компонент шума обусловлено работой системы движения корабля, винтов и вспомогательных механизмов. В зависимости от своего происхождения различные ДС могут зависеть (либо не зависеть) от скорости хода, глубины погружения шумящего объекта и ряда других факторов.

Характеристики ДС, обусловленных работой вспомогательных механизмов, обычно стабильны и не зависят от скорости движения корабля. Частоты и амплитуды ДС, вызванных энергетической установкой и гребными винтами, изменяются вместе со скоростью движения корабля. Спектральные функции таких ДС испытывают мультипликативные преобразования, пропорциональные изменению скорости вращения линии вала.

В некоторых случаях ДС, возбуждаемые от одного и того же источника, бывают синхронизированы между собой и образуют т.н. звукоряды (ЗР), т.е. наборы ДС, частоты которых кратны между собой. Такие ДС в литературе часто называют гармониками.

Так, например, вальный ЗР может содержать ДС на частотах, кратных частоте вращения линии вала:

где k=1, 2, 3, …, K - номера гармоник;

v - скорость вращения вала (об/мин);

f_в1 - частота вращения вала (Гц).

Лопастной ЗР может содержать ДС на частотах, кратных произведению частоты вращения линии вала и числа лопастей винта:

где z - число лопастей на винте.

Тональные компоненты ЗР являются высокостабильными и имеют очень узкие полосы частот [1-6]. Уместно заметить, что в отличие от отдельных ДС шум в виде ЗР, несмотря на то, что содержит узкополосные составляющие, в целом представляет собой широкополосный шумовой процесс.

Узкополосный гидроакустический шум (т.е. ДС общего суммарного шума) движущегося в воде объекта является полезным сигналом, обнаруживаемым на фоне помех, для узкополосных систем шумопеленгования.

Основной характеристикой, используемой для описания моделей ДС шума гидроакустических целей, является их спектральная плотность мощности. При этом в известных способах и устройствах обнаружения узкополосных шумовых сигналов (при синтезе алгоритмов обработки) традиционно используются идеализированные модели СПМ ДС. Эти же способы и реализующие их устройства приема используются в настоящее время и для обнаружения широкополосных шумов в виде звукорядов из кратных гармоник (1-2).

Наиболее часто СПМ отдельной ДС упрощенно представляется в виде абсолютно узкой δ-функции, сдвинутой от начала координат («нулевой частоты») на значение центральной частоты ДС f₁ [1-4]:

Соответственно, СПМ звукоряда из К ДС представляется в виде ряда δ-функций, сдвинутых на кратные частотные интервалы kf₁ [1-4]:

В случае более реалистичного подхода (с заданием конкретного значения ширины эффективной полосы ДС Δf) СПМ данной ДС может быть описана в виде локальной спектральной функции G₀(f), сдвинутой от начала координат («нулевой частоты») на значение центральной частоты ДС f₁ и, соответственно, локализованной в районе ее центральной частоты f₁

В большинстве случаев для упрощения моделей ДС предполагается, что форма спектральной функции G₀(f) представляет собой узкополосную прямоугольную функцию вида [1]:

где - стандартная прямоугольная функция [1, с.143].

СПМ звукоряда из К ДС в этом случае представляется в виде ряда сдвинутых узкополосных спектральных функций G₀(f) (отличных от δ-функций) с постоянной шириной полосы ДС Δf=const:

где G₀(f) - узкополосная спектральная функция, заданная в области нулевой частоты;

f₁ - центральная частота первой гармоники звукоряда;

G_k (f)=G₀(f-kf₁) - СПМ k-й гармоники;

А_k - амплитуда k-й гармоники;

К - количество ДС в звукоряде.

Для модели G₀(f) в виде прямоугольной функции, соответственно, можно записать

где

В качестве модели G₀(f) могут рассматриваться и другие, более сложные, локализованные спектральные функции, в виде различных «спектральных окон», соответствующих известным «временным (корреляционным) окнам» (прямоугольному, Бартлетта, Парзена, Хеннинга, Хемминга и т.д. [8,22]), но также с постоянной шириной полосы ДС: Δf_k=Δf=const.

При данном традиционном подходе, т.е. при использовании моделей ДС и ЗР вида (3-8), преобразования спектральных функций отдельных ДС и их звукорядов (вызванных системой движения корабля) при изменении скорости хода (частоты вращения вала) могут быть описаны только приближенно - с помощью обычного сдвига по частоте.

В соответствии с принятыми моделями (3, 4) или (5-8), в известных способах обнаружения узкополосных шумовых гидроакустических сигналов (соответствующих ДС спектра шумоизлучения пеленгуемых объектов) и в реализующих их устройствах (т.е. в узкополосных гидроакустических системах шумопеленгования) применяются различные способы спектрального анализа (методы оценки СПМ шума), основанные на преобразовании Фурье [7, 8]. Как уже говорилось выше, эти же способы и реализующие их устройства приема используются и для обнаружения широкополосных шумов в виде звукорядов, состоящих из кратных гармоник (1-2).

Известный способ обнаружения узкополосного шума с дискретными компонентами СПМ и реализующее его устройство, по сути, являются многоканальным энергетическим приемником (аналог) [1, с.351-352]. Данный способ представляет собой последовательное выполнение операций: широкополосной полосовой фильтрации (для формирования общего частотного диапазона), многоканальной узкополосной полосовой фильтрации (для формирования отдельных частотных каналов), квадратичного детектирования, интегрирования и сравнения с порогом (в каждом частотном канале).

Данный способ может быть непосредственно применен в устройствах-обнаружителях с аналоговым исполнением, в которых легко реализуется один из классических методов спектрального анализа - «метод фильтрации».

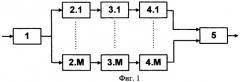
Устройство (аналог) [1, с.351-352], реализующее указанный способ обнаружения узкополосного шума, приведено на фиг.1, где

блок 1 - широкополосный полосовой фильтр;

блоки 2.1-1.М - набор («гребенка») узкополосных полосовых фильтров (УПФ), с одинаковой шириной полосы пропускания и различными центральными частотами (с равномерным шагом по частоте, равным ширине полосы пропускания одного фильтра);

блоки 3.1-3.М - квадратичные детекторы;

блоки 4.1-4.М - интеграторы;

блок 5 - М-канальное пороговое устройство.

Принцип действия данного устройства заключается в следующем. На вход устройства поступает реализация входного процесса

где s(t) - обнаруживаемый узкополосный шумовой сигнал,

n(t) - аддитивная помеха в виде нормального белого шума,

которая поступает на вход широкополосного полосового фильтра (ШПФ) (блок 1), формирующего общий частотный диапазон анализируемого шумового сигнала.

С выхода ШПФ (блок 1) полосовой шумовой процесс поступает на входы М-канальной гребенки УПФ (блоки 2.1-2.М), где формируется М отдельных частотных каналов.

Сформированные (расфильтрованные) узкополосные шумовые процессы у_m(t) поступают на входы квадратичных детекторов (блоки 3.1-3.М), с выходов которых продетектированные и возведенные в квадрат узкополосные сигналы |y_m(t)|² поступают на входы интеграторов (блоки 4.1-4.М). Время интегрирования (или накопления) узкополосных сигналов обычно выбирается равным величине, обратно-пропорциональной ширине полосы пропускания УПФ [1], и обеспечивающим потенциальную разрешающую способность по частоте для данного способа спектрального анализа (метода фильтрации).

С выходов интеграторов выделенные отклики z_m(t) поступают на вход М-канального порогового устройства (блок 5), выход которого является выходом устройства.

Способы обнаружения узкополосных шумовых сигналов, реализуемые в современных цифровых узкополосных шумопеленгаторных системах, основаны на т.н. «алгоритмах оценивания СПМ» [7, 8] (в основе которых также лежит преобразование Фурье). Т.е. в современных узкополосных приемниках (с цифровой реализацией) «гребенка узкополосных фильтров» формируется за счет вычисления дискретного преобразования Фурье (обычно реализуемого с помощью алгоритмов быстрого преобразования Фурье (БПФ)) входного сигнала или его корреляционной функции.

Форма АЧХ «узкополосных фильтров цифровой гребенки» определяется спектральной функцией временного окна, используемого при обработке входных данных.

Способ обнаружения узкополосных шумовых сигналов на основе «косвенного алгоритма» спектрального оценивания (аналог) [7, с.453-454] представляет собой последовательное выполнение операций: отбеливания, вычисления автокорреляционной функции, умножения на функцию «временного окна», вычисления преобразования Фурье и сравнения с порогом (в каждом частотном канале).

Способ обнаружения узкополосных шумовых сигналов, основанный на т.н. «прямом алгоритме» оценки СПМ анализируемого сигнала [7, с.454-455], представляет собой последовательное выполнение операций: секционирования входных данных, «взвешивания» (умножения на функцию «временного окна»), вычисления преобразования Фурье (по секциям), вычисления квадрата модулей комплексных коэффициентов Фурье, осреднения (по секциям) и сравнения с порогом (в каждом частотном канале).

Первые три перечисленные операции, в целом, представляют собой одну более общую операцию, называемую в технической литературе различными синонимами: «оконное преобразование Фурье», «кратковременное преобразование Фурье» («short-time Fourier transform» (STFT)), вычисление «периодограммы» или «спектрограммы» [7-9]. Причем промежуточная операция «взвешивания» выборки (секции) данных (т.е. умножения на функцию окна с целью уменьшения значений временных отсчетов по краям выборки и, соответственно, снижения уровня боковых лепестков узкополосных спектральных составляющих) может быть исключена. В этом случае используется самое простое - прямоугольное окно, образуемое автоматически при выполнении операции секционирования исходных данных.

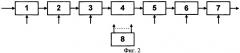
Устройство (аналог) [7, с.456-457], реализующее вышеописанный способ обнаружения узкополосных шумовых сигналов, приведено на фиг.2, где

блок 1 - аналого-цифровой преобразователь (АЦП);

блок 2 - рециркулятор;

блок 3 - вычислитель быстрого преобразования Фурье (БПФ);

блок 4 - вычислитель квадрата модуля;

блок 5 - оперативное запоминающее устройство (ОЗУ);

блок 6 - устройство осреднения;

блок 7 - пороговое устройство;

блок 8 - управляющее устройство.

Принцип действия данного устройства заключается в следующем. На вход устройства поступает реализация входного процесса x(t), которая поступает на вход АЦП (блок 1) с частотой дискретизации, удовлетворяющей требованиям теоремы Котельникова:

С выхода АЦП (блок 1) дискретные отсчеты поступают на вход рециркулятора (блок 2), где формируется и с каждым новым отсчетом обновляется текущая дискретная выборка (секция) x(n) длиной N отсчетов. Длина выборки N (и, соответственно, время анализа Т=NΔt_Д) определяется требуемой разрешающей способностью по частоте Δf (и, соответственно, шириной полосы элементарного частотного канала) обнаружителя ДС:

Сформированная текущая дискретная выборка входного процесса x(n) поступает на вход вычислителя БПФ (блок 3), с выхода которого комплексный спектр X(n) текущей выборки поступает на вход вычислителя квадрата модуля (блок 4), с выхода которого вычисленные квадраты модуля спектра текущей выборки |X(n)|² поступают на вход буферного ОЗУ (блок 5). В ОЗУ накапливается М последовательно вычисленных текущих массивов |X_m(n)|². После накопления М вычисленных реализаций квадратов модуля спектра, с выходов ОЗУ (блок 5) считывается М одномерных массивов длиной N отсчетов и поступает на устройство осреднения (блок 6), где вычисляется текущая осредненная оценка СПМ входного процесса:

С выхода устройства осреднения (блок 6) текущая осредненная оценка СПМ поступает на вход порогового устройства (блок 7), выход которого является выходом устройства.

Устройство управления (блок 8) осуществляет синхронизацию работы: аналого-цифрового преобразователя (блок 1), рециркулятора (блок 2), вычислителя преобразования Фурье (блок 3), оперативного запоминающего устройства (блок 5), устройства осреднения (блок 6) и порогового устройства (блок 7).

Недостатком вышеописанных способов обнаружения узкополосных сигналов и соответствующих устройств (аналогов) является их низкая реальная помехоустойчивость, несоответствующая теоретическому (потенциальному) выходному отношению сигнал/помеха (ОСП), вычисляемому на основе гипотезы идеально узкой ДС (3-4) или же ДС с постоянной шириной полосы частот, не зависящей от частоты (5-8).

Разрешающая способность методов спектрального анализа, используемых в данных способах обнаружения узкополосных сигналов и в соответствующих устройствах (аналогах), является фиксированной для всего рассматриваемого частотного диапазона и, в целом, равна величине, обратной длительности анализируемого временного процесса (времени наблюдения, определяемого т.н. «временным окном»).

Недостаточная помехоустойчивость данных способов обнаружения узкополосных сигналов является следствием использования идеализированной модели СПМ узкополосного шума в виде ДС, которая не учитывает всю известную информацию об обнаруживаемом сигнале.

В то же время известно, что при решении задачи обнаружения шумовых сигналов на фоне помехи, в случае известных зависимостей СПМ сигнала G_c(f) и помехи G_П(f), оптимальным является энергетический приемник (квадратичный детектор и интегратор), с предварительным (преддетекторным) фильтром Эккарта [1, с.348-351; 13, с.284-285].

Максимум обобщенного отношения сигнал/помеха (ОСП) на выходе энергетического приемника с предварительной додетекторной фильтрацией (определяемого как отношение приращения математического ожидания выходного процесса z₁(t), обусловленного наличием полезного сигнала во входном процессе, к дисперсии выходного процесса в случае отсутствия сигнала Z₀(t)) [1, с.351]:

имеет место, если квадрат модуля передаточной характеристики преддетекторного фильтра имеет вид:

Выражение (14) определяет вид АЧХ (форму квадрата модуля передаточной характеристики) оптимального преддетекторного фильтра, называемого в технической литературе фильтром Эккарта [1, с.348-351; 13, с.284-285].

Если помеха не является белым шумом, характеристика оптимального фильтра должна иметь спад в тех областях спектра, где мощность помехи велика. В присутствии белого шума (т.е. при равномерном спектре помехи) форма квадрата модуля передаточной характеристики оптимального преддетекторного фильтра Эккарта должна совпадать со спектральной плотностью мощности обнаруживаемого шумового сигнала |H(f)|²=G_c(f).

В узкополосном случае (т.е. при обнаружении ДС шума) помеху (в пределах ширины полосы частот СПМ ДС) можно с большой достоверностью считать белым шумом с равномерной СПМ G_П(f)=const. Следовательно, АЧХ узкополосного преддетекторного фильтра в каждом частотном канале, в идеале, должна повторять форму СПМ ДС узкополосного шума. В противном случае будут иметь место потери помехоустойчивости по сравнению с оптимальным приемником - многоканальным энергетическим приемником с преддетекторными фильтрами Эккарта [1, 13] в каждом частотном канале.

Таким образом, применение более точной модели обнаруживаемого узкополосного шума в виде отдельной ДС (с неизвестной центральной частотой) или широкополосного шума в виде звукоряда ДС (с кратными частотами) позволит реализовать обнаружение ДС или образуемых ими ЗР с более высокой помехоустойчивостью.

В действительности, входной процесс x(t) обнаружителя узкополосных шумовых гидроакустических сигналов обладает более сложной структурой СПМ, чем в общепринятых моделях (3-8).

Как отмечают авторы работ [1 (с.322), 21 (с.46)], эффективная ширина полосы СПМ ДС Δf зависит от значения частоты, на которой она образуется. Причем она прямо пропорциональна центральной частоте ДС f=f₁ и составляет 0,03…0,3% от значения f₁.

Случайные искажения, вносимые гидроакустическим каналом при распространении сигнала, а также доплеровские преобразования, вызванные кинематикой шумящего объекта и носителя ГАС шумопеленгования, приводят к дополнительному уширению полосы Δf до ≈0,5% от значения f₁. Но при этом сохраняются масштабно-частотные свойства СПМ отдельных ДС или общей СПМ всего звукоряда. Т.е. относительная полоса СПМ каждой отдельной ДС (или ДС, входящих в состав звукоряда, образованного одним общим источником) всегда является постоянной величиной и имеет порядок:

Другими словами, эффективная полоса ДС является линейной функцией ее центральной частоты:

Соответственно, эффективная полоса каждой k-й гармоники в звукоряде также является линейной функцией частоты:

а общая СПМ всего звукоряда из К ДС обладает масштабными (мультипликативными) свойствами в области частоты.

Данные соотношения могут быть положены в основу более точной (масштабно-частотной) модели СПМ узкополосного шума в виде отдельной ДС или широкополосного шума в виде ЗР ДС, учитывающей масштабные свойства ДС [20].

Спектральная функция отдельной ДС с центральной частотой f₁ может быть представлена в виде:

где G₀(f) - моделирующая спектральная функция, локализованная в области нулевой частоты (задающая общую форму СПМ ДС);

α₀ - масштабный коэффициент, соответствующий мультипликативному преобразованию (сжатию) исходной спектральной функции G₀(f);

f₁ - сдвиг частоты, соответствующий конкретному значению центральной частоты ДС.

Выбранные значения α₀ и f₁ однозначно определяют требуемую относительную полосу ДС β (15).

Для широкополосного шума в виде звукоряда из К ДС масштабно-частотную модель СПМ можно описать путем представления общей спектральной функции ЗР в виде суммы расширяющихся в кратное число раз спектральных функций первой гармоники, где в качестве масштабного коэффициента выступает номер гармоники k:

Уместно заметить, что при рассмотрении спектральной плотности давления (СПД) G_P(f), измеряемой в (вместо спектральной плотности мощности G(f), измеряемой будет справедлива запись амплитудных масштабных коэффициентов под знаком радикала:

- для СПД отдельной ДС

- для СПД ЗР из N ДС

При моделировании случайную временную реализацию узкополосного шума s(t), соответствующего модели СПД в виде отдельной ДС (20) или в виде звукоряда (21), можно получить путем пропуска реализации нормального белого шума w(t) через фильтр с передаточной характеристикой вида (20) или (21) соответственно:

где F^-1 { } - оператор обратного преобразования Фурье.

В качестве модели спектральной плотности давления отдельной ДС или первой ДС (первой гармоники) общего звукоряда может быть принята спектральная функция в виде сжатой в α₀ раз и сдвинутой на величину f₁ (Гц) функции Гаусса:

Данная функция, при своей простоте, достаточно хорошо описывает конечный вид СПМ ДС на входе приемника-обнаружителя с учетом:

- влияния нестабильности вращения различных корабельных механизмов со средней частотой f₁;

- влияния зависимости АЧХ механических контуров (корабельных конструкций) на формируемый спектр излучаемого узкополосного шума;

- влияния доплеровских мультипликативных (масштабных) преобразований за счет движения излучающего объекта и носителя ГАС шумопеленгования;

- случайных амплитудно-частотно-фазовых искажений за счет влияния канала распространения, описываемых с помощью свертки СПМ сигнала с функцией рассеяния канала и приводящих к дополнительному уширению СПМ ДС.

Уместно заметить, что спектральная функция вида (24) является отмасштабированным спектром Фурье известного комплексного аналитического вейвлета Морле [14-17]:

Спектр Фурье данного типа вейвлетов имеет вид:

где 1₊(f) - функция Хевисайда.

Частотный сдвиг f₁(Гц) в модели СПД (20) задает центральную частоту ДС, а подбор значения масштабного коэффициента α₀ позволяет получить требуемую величину относительной полосы ДС .

Несмотря на наличие описанных выше мультипликативных свойств ДС и ЗР, в традиционных методах спектрального анализа, применяемых в известных способах и устройствах обнаружения узкополосных сигналов (аналогах), разрешающая способность (по частоте) является постоянной (фиксированной) величиной для всего частотного диапазона. При ее настройке (за счет выбора размера и формы временного окна) на ширину спектра самой узкой (низкочастотной) ДС (в анализируемом диапазоне частот) полоса анализа будет слишком узкой для более высокочастотных ДС звукоряда. При ее настройке на ширину спектра более высокочастотных ДС полоса анализа будет избыточна (слишком широка) для более низкочастотных ДС.

Таким образом, в классических обнаружителях шумового сигнала в виде отдельных ДС или в виде звукорядов ДС с кратными частотами, использующих различные методы аналогового или цифрового спектрального анализа (на основе преобразования Фурье), принципиально невозможно обеспечить переменную разрешающую способность по частоте (во всем анализируемом диапазоне частот), соответствующую масштабно-частотной модели СПМ ДС (18-19). Т.е. в рамках классического спектрального анализа невозможно реализовать передаточные характеристики преддетекторных фильтров, адаптированные для различных частотных каналов всего диапазона и, таким образом, невозможно достичь максимума ОСП (13), соответствующего фильтру Эккарта.

Устройство обнаружения узкополосных шумовых гидроакустических сигналов на основе вычисления интегрального вейвлет-спектра [20] (прототип), позволяет более точно учесть масштабные свойства СПМ ДС гидроакустических шумящих объектов и повысить помехоустойчивость соответствующих приемников-обнаружителей. Это достигается за счет применения к входному процессу вместо общепринятого кратковременного преобразования Фурье (с «грубой» (равномерной) разрешающей способностью во всем частотном диапазоне) нового вида преобразования, а именно непрерывного вейвлет-преобразования (с адаптированной разрешающей способностью (полосой анализа) в соответствии с масштабными свойствами обнаруживаемого узкополосного сигнала), с последующим осреднением по времени квадрата модуля полученного результата вейвлет-преобразования. В научной литературе совокупность указанных операций называется вычислением «интегрального вейвлет-спектра» [18] или «скалограммой» (scalogram) [15] входного анализируемого процесса.

Непрерывное вейвлет-преобразование (НВП) может быть определено в виде скалярного произведения исследуемого процесса x(t) и специальных базисных вейвлет-функций ψ_ατ(t) [14-17]:

где черта сверху обозначает операцию комплексного сопряжения.

Общий принцип построения базиса вейвлет-преобразования состоит в использовании мультипликативных преобразований с параметром масштаба α и смещений с параметром сдвига τ исходной вейвлет-функций ψ(t) (т.н. материнского вейвлета):

Чтобы быть вейвлетом, базисные функции должны обладать рядом необходимых свойств [14-17]. Они должны быть: квадратично-интегрируемыми, знакопеременными (обладать нулевым средним), а также должны стремиться к нулю на ±∞, и для практических целей - чем быстрее, тем лучше (причем вейвлет должен быть хорошо локализован и во времени, и по частоте). Для того чтобы было возможно обратное вейвлет-преобразование, спектральная функция вейвлета ψ(f) должна удовлетворять еще одному условию:

Формула непрерывного обратного вейвлет-преобразования имеет вид:

С целью более эффективного вычисления (при цифровой реализации) оператор НВП (24) может быть определен в частотной области [19] (аналог) в виде:

где Ψ(f)=F{ψ(t)} - образ Фурье выбранного исходного вейвлета ψ(t);

X(f)=F{x(t)} - образ Фурье анализируемого процесса x(t).

При этом достигается значительное повышение быстродействия цифровых устройств, реализующих НВП, за счет вычисления сверток с помощью эффективных процедур БПФ.

Единственным ограничением для данной формы записи оператора НВП (31), по сравнению с (27), является требование аналитичности для исследуемого сигнала и применяемого вейвлета:

supp Х_A(f)⊂[0,∞); supp Ψ_A(f)⊂[0,∞),

т.е. X_A(f)=0 и Ψ_A(f)=0 при f≤0.

В случае вейвлет-анализа действительных сигналов (что имеет место при обработке гидроакустических сигналов) их легко представить в аналитическом виде, без потери информации, путем обнуления отрицательных частот их комплексных спектров Фурье. То же самое касается и используемых вейвлетов. Причем часть широко применяемых комплексных вейвлетов (например, вейвлет Морле [14-17]) уже по определению сами являются аналитическими сигналами.

В принципе, для реализации оператора (31) достаточно, чтобы аналитическим был только вейвлет, т.к. свертка анализируемого сигнала с аналитическим вейвлетом (что соответствует перемножению их спектров Фурье) в итоге также дает результирующий аналитический сигнал.

В настоящее время применяется большое количество различных семейств вейвлетов: Хаара, Добеши, Морле, FHAT, МНАТ и т.д. [14-17]. Выбор типа анализирующего вейвлета, как правило, определяется тем, какую информацию необходимо извлечь из сигнала и степенью схожести вейвлета и анализируемого сигнала. Каждый вейвлет имеет свои характерные особенности во временной и частотной области. С помощью различных типов вейвлетов можно полнее выявить и подчеркнуть те или иные свойства анализируемого сигнала в масштабно-временной области. Как уже говорилось выше, для реализации способа обнаружения узкополосных шумовых сигналов [20] (прототип) достаточно эффективно может быть использован комплексный аналитический вейвлет Морле (25).

Вейвлет-спектр W_x(α,τ) одномерного процесса x(t), полученный в результате применения оператора НВП (27) или (31), является двумерной функцией и представляет собой поверхность в трехмерном пространстве.

Отметим, что при анализе комплексного сигнала или при использовании комплексного вейвлета, в результате вейвлет-преобразования получается комплексный вейвлет-спектр, и соответственно - двумерные массивы значений модуля и фазы (или реальной и мнимой части) вейвлет-коэффициентов:

.

Результат интегрального осреднения квадрата модуля НВП сигнала |W_x(α,τ)|² за время наблюдения для всех масштабов α является одномерной функцией масштаба и называется интегральным вейвлет-спектром сигнала [18] или скалограммой [15]:

Интегральный вейвлет-спектр сигнала x(t) по своей физической сущности очень близок к оценке его СПМ , получаемой на основе осреднения результатов оконного (кратковременного) преобразования Фурье. При этом масштабы α вейвлет-преобразования (при известном (заданном) базовом материнском вейвлете ψ(t)) однозначно соответствуют частотам f спектра Фурье.

Интерес для цифровой обработки сигналов представляет дискретный вариант НВП [14-19]. Необходимая дискретизация значений α и τ, при сохранении возможности восстановления сигнала из его преобразования, должна осуществляться следующим образом:

Вместо экспоненциальной формы дискретизации масштабных коэффициентов α возможна и линейная дискретизация вида:

Вариант базиса вейвлетов (28) с дискретизацией параметров α и τ (33) записывается в виде:

и в математической литературе называется «фреймами» [14].

Шкала масштабов вейвлет-спектра однозначно соответствует частотам Фурье исследуемого сигнала. Поэтому вейвлет-преобразование можно трактовать как особый вид «частотно-временного представления» сигналов [9]. Хотя точнее его следует называть «масштабно-временным представлением».

Причем линейная шкала масштабов (31), хотя и более избыточна по сравнению с логарифмической (30), но более удобна для сравнения результатов вейвлет-преобразования (т.е. масштабно-временного представления сигналов) с различными видами частотно-временных представлений сигналов [9].

Сущность математического метода, положенного в основу устройства обнаружения узкополосных шумовых гидроакустических сигналов на основе вычисления интегрального вейвлет-спектра [20] (прототипа) заключается в проведении следующих операций:

1. Вычисление вейвлет-преобразования W_x(α,τ) входного процесса x(t) (наиболее эффективно эта процедура реализуется в частотной области с использованием аналитического вейвлета, в соответствии с оператором (31)):

1.1. Выбор исходного вейвлета Ψ(t), вычисление его спектра Фурье ψ(f), комплексное сопряжение и обнуление отрицательных частот (приведение к аналитическому виду): , при f>0 и , при f≤0 (в случае выбора комплексного аналитического вейвлета, последняя процедура - обнуления отрицательных частот, необязательна).

1.2. Вычисление базиса спектров аналитических вейвлетов путем масштабирования исходного спектра материнского вейвлета: .

1.3. Вычисление спектра Фурье входного процесса X(f).

1.4. Перемножение спектра Фурье входного процесса X(f) с сопряженным базисом отмасштабированных спектров аналитических вейвлетов .

1.5. Вычисление обратного преобразования Фурье от результата последнего перемножения:

2. Вычисление квадрата модуля результата вейвлет-преобразования входного процесса x(t).

3. Осреднение по времени квадрата модуля результата вейвлет-преобразования входного процесса x(t):

4. Сравнение полученного интегрального вейвлет-спектра с порогом (выбираемым в зависимости от требуемой вероятности ложной тревоги) и принятие решения об обнаружении сигнала в случае превышения порога в одном или нескольких каналах (гипотеза Н₁), либо о не обнаружении - в случае не превышения порога (гипотеза H₀) ни в одном из каналов.

Операции 1.1 и 1.2 производятся только с вейвлетом ψ(t), а не с исследуемым входным процессом x(t), и таким образом, данные операции могут быть проведены заранее, а результаты их расчетов - храниться в ПЗУ.

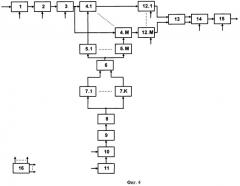
Устройство обнаружения узкополосных шумовых гидроакустических сигналов на основе вычисления интегрального вейвлет-спектра [20] (прототип), приведено на фиг.3, где

блок 1 - аналого-цифровой преобразователь (АЦП);

блок 2 - рециркулятор;

блок 3 - первый вычислитель БПФ;

блоки 4.1-4.М - комплексные перемножители;

блоки 5.1-5.M - масштабирующие устройства с коэффициентами сжатия

блок 6 - устройство комплексного сопряжения;

блок 7 - устройство обнуления отрицательных частот;

блок 8 - второй вычислитель БПФ;

блок 9 - постоянное запоминающее устройство (ПЗУ);

блоки 10.1-10.М - вычислители обратного БПФ;

блок 11 - вычислитель квадрата модуля;