Устройство идентификации параметров динамических систем на основе вариационных принципов

Устройство идентификации параметров динамических систем на основе вариационных принципов

Иллюстрации

Показать все

Реферат

Изобретение относится к цифровой вычислительной технике и предназначено для идентификации параметров динамических систем.

Цель изобретения - повышение точности идентификации параметров динамических систем и увеличение скорости сходимости оценок к истинным параметрам.

Одним из способов повышения эффективности алгоритмов идентификации является использование естественных, природных свойств объекта в виде вариационных принципов, которые справедливы для всех форм существования материи и являются выражением фундаментальных законов сохранения, выступающих инвариантами в тех предметных областях, к которым относится исследуемый объект [1].

В данном устройстве в качестве такого принципа выступает соотношение, справедливое для голономных систем и аналогичное принципу Гамильтона - Остроградского при наличии непотенциальных сил [2], из которого вытекают уравнения динамики объекта в форме дифференциальных уравнений Лагранжа второго рода. Использование такого соотношения в совокупности с аппаратом асинхронной вариации дает эффективный в плане точности оценок, скорости сходимости и снижения вычислительных затрат алгоритм идентификации. Это весьма важно на всех этапах создания, экспериментальной обработки и эксплуатации цифровой вычислительной техники, автоматических и автоматизированных систем и др. техники.

Рассмотрим общую постановку задач данного типа.

Пусть уравнение состояния динамической системы известно и имеет следующий вид:

, , ,

где z∈R^m - вектор неизвестных постоянных параметров,

- вектор-функция, непрерывная вместе со своими частными производными,

m - натуральное число.

Динамика идентифицируемых параметров z описывается уравнением

, z(0)=z₀,

где η∈R^m - вектор неизвестных неслучайных возмущений, удовлетворяющий требованиям физической реализуемости .

Уравнение наблюдения имеет вид

y=H(х,t)+n(t),

где y∈R^k - вектор наблюдения,

H(x,t) - непрерывная вместе с частными производными вектор-функция,

k - натуральное число,

n(t) - вектор белого гауссовского шума.

Поставим задачу определения оценки вектора z из условия минимума функционала невязки

.

Согласно [3] для рассмотренной постановки задачи получены рекуррентные уравнения последовательной идентификации, которые имеют вид

где N - матрица односторонней спектральной плотности шума наблюдения,

α - параметр регуляризации,

µ - неопределенный множитель Лагранжа,

G - матрица чувствительности системы по вектору параметров z,

P - некоторая матрица размера m×m,

n - натуральное число.

Эффективность разрабатываемого устройства подтверждается следующими вычислительными экспериментами.

Пример 1. Рассмотрим задачу идентификации двух линейных параметров динамической системы, которая описывается дифференциальным уравнением второго порядка

где x(t), - эквивалент координаты и скорости динамической системы;

z₀ и z₁ - определяемые параметры.

Уравнение наблюдения имеет вид

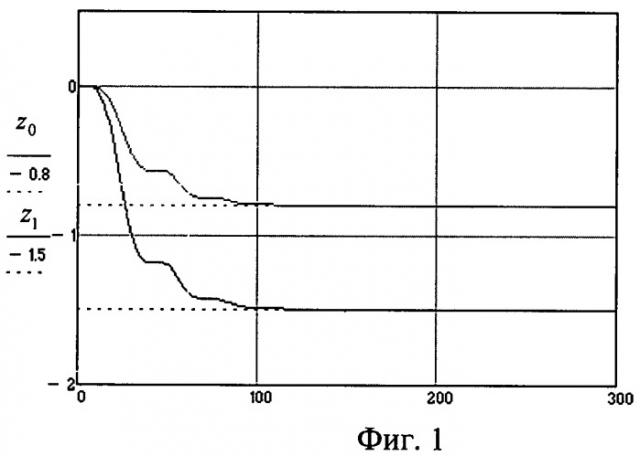
Требуется идентифицировать параметры z₀ и z₁, истинные значения которых z₀=-0.8, z₁=-1.5 из условия минимума целевого функционала

Алгоритм идентификации (1) для данной системы (2) определяется как

Результаты численного моделирования представлены на фигурах 1, 2, 3. Для сравнения на фигурах продемонстрирована идентификация параметров z₀, z₁ с помощью расширенного фильтра Калмана.

В установившемся режиме определяется относительная погрешность идентификации первого и второго параметров 0.1%, 0.4% соответственно для разработанного метода и 0.6%, 0.5% для расширенного фильтра Калмана.

Анализ результатов численного моделирования показывает, что решение задачи идентификации на основе вариационных принципов позволяет получить увеличение в сравнении с Калманом скорости сходимости и точности получаемых оценок параметров.

Пример 2. Рассмотрим задачу идентификации параметра z₁=0.1 в системе второго порядка

гдe a(t)=2e^-0.1t.

Уравнение наблюдения (3) идентично предыдущему примеру.

Предполагается, что форма a(t) известна, но неизвестно начальное значение и масштаб отсчета времени, т.е.

.

Требуется идентифицировать параметр z₁ динамической системы из условия минимума (4).

Алгоритм идентификации (1) для данной системы (6) определяется следующим образом

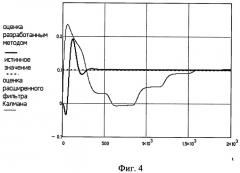
Результаты вычислительного эксперимента представлены на фигуре 4. На фигуре 4 приведены графики сравнения динамики оценки z₁, полученные с помощью расширенного фильтра Калмана и разработанного алгоритма.

Анализ результатов численного моделирования показывает, что решение задачи идентификации на основе вариационных принципов имеет высокую точность и скорость сходимости в сравнении с фильтром Калмана.

Также подтверждает эффективность разработанного устройства еще один вычислительный эксперимент [5], проведенный с использованием зарегистрированных в ФГУ ФИПС [6, 7] программ для ЭВМ.

Приведенные результаты позволяют утверждать, что идентификация параметров на основе вариационных принципов обеспечивает увеличение точности и скорости сходимости оценок в сравнении с известным фильтром Калмана.

Сущность изобретения, полученного на основе уравнений (1), поясняется на фиг.5 и фиг.6, где представлены структурные схемы устройства идентификации и первого блока интегрирования.

На фиг.5 представлена структурная схема устройства идентификации на основе вариационных принципов. Устройство содержит блок хранения констант 1.1; первый блок 2.1, второй блок 2.2 формирования функции; первый блок 3.1, второй блок 3.2, третий блок 3.3, четвертый блок 3.4, пятый блок 3.5 формирования производной; первый блок 4.1, второй блок 4.2, третий блок 4.3, четвертый блок 4.4, пятый блок 4.5, шестой блок 4.6, седьмой блок 4.7, восьмой блок 4.8, девятый блок 4.9, десятый блок 4.10, одиннадцатый блок 4.11 формирования умножения; первый блок 5.1, второй блок 5.2, третий блок 5.3 формирования разности; первый блок 6.1, второй блок 6.2 формирования суммы; первый блок 7.1, второй блок 7.2 транспонирования; первый блок 8.1, второй блок 8.2, третий блок 8.3, четвертый блок 8.4, пятый блок 8.5, шестой блок 8.6 интегрирования.

На фиг.6 представлена структурная схема первого блока интегрирования, которая содержит блок 8.1.1 формирования умножения, блок 8.1.2 формирования суммы, линию задержки 8.1.3.

На первый информационный вход блока 1.1 хранения констант (фиг.5) поступает значение наблюдаемой величины; первый информационный выход блока 1.1 хранения констант соединен с первым информационным входом первого блока 4.1 формирования умножения; второй, третий и четвертый информационные выходы блока 1.1 хранения констант соединены соответственно с первым, вторым и третьим информационными входами первого блока 2.1 формирования функции; второй и четвертый информационные выходы блока 1.1 хранения констант соединены соответственно со вторым и первым информационными входами второго блока 2.2 формирования функции; пятый информационный выход блока 1.1 хранения констант соединен со вторыми информационными входами первого 8.1, второго 8.2, третьего 8.3, четвертого 8.4, пятого 8.5 и шестого 8.6 блоков интегрирования; шестой информационный выход блока 1.1 хранения констант соединен с первым информационным входом второго блока 5.2 формирования разности; седьмой информационный выход блока 1.1 хранения констант соединен с первым информационным входом второго блока 4.2 формирования умножения; восьмой информационный выход блока 1.1 хранения констант соединен с первым и вторым информационными входами соответственно пятого блока 4.5 и восьмого блока 4.8 формирования умножения; девятый информационный выход блока 1.1 хранения констант соединен с первым информационным входом второго блока 7.2 транспонирования, а также с первым и вторым информационными входами соответственно восьмого блока 4.8 и седьмого блока 4.7 формирования умножения; десятый информационный выход блока 1.1 хранения констант соединен со вторым информационным входом шестого блока 4.6 формирования умножения; одиннадцатый и двенадцатый информационные выходы блока 1.1 хранения констант соединены соответственно со вторым и первым информационными входами одиннадцатого блока 4.11 формирования умножения, информационный выход которого соединен с первым информационным входом третьего блока 5.3 формирования разности; информационный выход первого блока 2.1 формирования функции соединен соответственно с первыми информационными входами первого блока 5.1 формирования разности, второго блока 3.2, третьего блока 3.3 и четвертого блока 3.4 формирования производной; информационный выход второго блока 2.2 формирования функции соединен с первым и вторым информационными входами соответственно первого блока 7.1 транспонирования и второго блока 5.2 формирования разности, информационный выход которого соединен со вторым информационным входом второго блока 4.2 формирования умножения, информационный выход которого соединен со вторым информационным входом третьего блока 4.3 формирования умножения; информационный выход первого блока 7.1 транспонирования соединен с первым информационным входом первого блока 3.1 формирования производной, информационный выход которого соединен с первым информационным входом третьего блока 4.3 формирования умножения, информационный выход которого соединен соответственно со вторыми информационными входами первого блока 4.1 и четвертого блока 4.4 формирования умножения и первым информационным входом пятого блока 3.5 формирования производной, информационный выход которого соединен со вторым информационным входом девятого блока 4.9 формирования умножения; информационный выход второго блока 7.2 транспонирования соединен со вторым информационным входом пятого блока 4.5 формирования умножения, информационный выход которого соединен соответственно с первыми информационными входами четвертого блока 4.4 и девятого блока 4.9 формирования умножения, информационный выход которого соединен с первым информационным входом десятого блока 4.10 формирования умножения; информационный выход восьмого блока 4.8 формирования умножения соединен со вторым информационным входом десятого блока 4.10 формирования умножения, информационный выход которого соединен со вторым информационным входом третьего блока 5.3 формирования разности, информационный выход которого соединен с первым информационным входом шестого блока 8.6 интегрирования, информационный выход которого соединен с первым и вторым информационными входами соответственно пятого блока 4.5 и восьмого блока 4.8 формирования умножения; информационный выход первого блока 4.1 формирования умножения соединен со вторым информационным входом первого блока 5.1 формирования разности, информационный выход которого соединен с первым информационным входом первого блока 8.1 интегрирования, информационный выход которого соединен со вторым информационным входом первого блока 2.1 формирования функции и первым информационным входом второго блока 8.2 интегрирования, информационный выход которого соединен с первым и вторым информационными входами соответственно первого блока 2.1 и второго блока 2.2 формирования функции; информационный выход четвертого блока 4.4 формирования умножения соединен с первым информационным входом третьего блока 8.3 интегрирования, с информационного выхода которого снимается значение искомого вектора идентификации параметров z и подается на первый и третий информационные входы соответственно второго блока 2.2 и первого блока 2.1 формирования функции; информационный выход второго блока 3.2 формирования производной соединен с первым информационным входом шестого блока 4.6 формирования умножения, информационный выход которого соединен с первым информационным входом первого блока 6.1 формирования суммы; информационный выход третьего блока 3.3 формирования производной соединен с первым информационным входом седьмого блока 4.7 формирования умножения, информационный выход которого соединен со вторым информационным входом первого блока 6.1 формирования суммы, информационный выход которого соединен с первым информационным входом второго блока 6.2 формирования суммы; информационный выход четвертого блока 3.4 формирования производной соединен со вторым информационным входом второго блока 6.2 формирования суммы, информационный выход которого соединен с первым информационным входом пятого блока 8.5 интегрирования, информационный выход которого соединен со вторым информационным входом шестого блока 4.6 формирования умножения и первым информационным входом четвертого блока 8.4 интегрирования, информационный выход которого соединен с первым информационным входом второго блока 7.2 транспонирования, а также с первым и вторым информационными входами соответственно восьмого блока 4.8 и седьмого блока 4.7 формирования умножения.

Информационный выход первого блока 5.1 формирования разности соединен с первым информационным входом блока 8.1.1 формирования умножения (фиг.6); пятый информационный выход блока 1.1 хранения констант соединен со вторым информационным входом первого 8.1 блока интегрирования, информационный выход которого соединен с первым информационным входом блока 8.1.2 формирования суммы; информационный выход линии задержки 8.1.3 соединен со вторым информационным входом блока 8.1.2 формирования суммы, с информационного выхода которого снимается значение первообразной и подается на первый вход линии задержки 8.1.3 и на второй информационный вход первого блока 2.1 формирования функции и первый информационный вход второго блока 8.2 интегрирования.

Блоки 8.2, 8.3, 8.4, 8.5, 8.6 интегрирования (фиг.5) имеют структуру и связи, аналогичные блоку 8.1, рассмотренному выше.

Устройство работает следующим образом. В исходном состоянии на вход устройства поступает y. В блоке 1.1 хранения констант записаны значения µ^-1, , , , Δt, N^-1, P, G, , α^-1, I. Значение µ^-1 с первого информационного выхода блока 1.1 хранения констант поступает на первый информационный вход первого блока 4.1 формирования умножения. Значение со второго информационного выхода блока 1.1 хранения констант поступает на первый информационный вход первого блока 2.1 формирования функции и на второй информационный вход второго блока 2.2 формирования функции. Значение с третьего информационного выхода блока 1.1 хранения констант поступает на второй информационный вход первого блока 2.1 формирования функции. Значение с четвертого информационного выхода блока 1.1 хранения констант поступает на третий информационный вход первого блока 2.1 формирования функции и на первый информационный вход второго блока 2.2 формирования функции. Значение Δt с пятого информационного выхода блока 1.1 хранения констант поступает на второй информационный вход первого 8.1, второго 8.2, третьего 8.3, четвертого 8.4, пятого 8.5 и шестого 8.6 блоков интегрирования. Значение y с шестого информационного выхода блока 1.1 хранения констант поступает на первый информационный вход второго блока 5.2 формирования разности. Значение N^-1 с седьмого информационного выхода блока 1.1 хранения констант поступает на первый информационный вход второго блока 4.2 формирования умножения. Значение P с восьмого информационного выхода блока 1.1 хранения констант поступает на первый информационный вход пятого блока 4.5 формирования умножения и второй информационный вход восьмого блока 4.8 формирования умножения. Значение G с девятого информационного выхода блока 1.1 хранения констант поступает на первый информационный вход второго блока 7.2 транспонирования, на первый информационный вход восьмого блока 4.8 формирования умножения и второй информационный вход седьмого блока 4.8 формирования умножения. Значение с десятого информационного выхода блока 1.1 хранения констант поступает на второй информационный вход шестого блока 4.6 формирования умножения. Значение α^-1 с одиннадцатого информационного выхода блока 1.1 хранения констант поступает на второй информационный вход одиннадцатого блока 4.11 формирования умножения. Значение I с двенадцатого информационного выхода блока 1.1 хранения констант поступает на первый информационный вход одиннадцатого блока 4.11 формирования умножения, с информационного выхода которого значение α^-1·I поступает на первый информационный вход третьего блока 5.3 формирования разности. Значение с информационного выхода первого блока 2.1 формирования функции поступает соответственно на первые информационные входы первого блока 5.1 формирования разности, второго блока 3.2, третьего блока 3.3 и четвертого блока 3.4 формирования производной. Значение с информационного выхода второго блока 2.2 формирования функции поступает соответственно на первый информационный вход первого блока 7.1 транспонирования и второй информационный вход второго блока 5.2 формирования разности, с информационного выхода которого значение поступает на второй информационный вход второго блока 4.2 формирования умножения, с информационного выхода которого значение поступает на второй информационный вход третьего блока 4.3 формирования умножения. Значение H^T с информационного выхода первого блока 7.1 транспонирования поступает на первый информационный вход первого блока 3.1 формирования производной, с информационного выхода которого значение поступает на первый информационный вход третьего блока 4.3 формирования умножения, с информационного выхода которого значение поступает на вторые информационные входы первого блока 4.1 и четвертого блока 4.4 формирования умножения и на первый информационный вход пятого блока 3.5 формирования производной, с информационного выхода которого значение поступает на второй информационный вход девятого блока 4.9 формирования умножения. Значение G^T с информационного выхода второго блока 7.2 транспонирования поступает на второй информационный вход пятого блока 4.5 формирования умножения, с информационного выхода которого значение PG^T поступает на первые информационные входы четвертого блока 4.4 и девятого блока 4.9 формирования умножения, с информационного выхода которого значение поступает на первый информационный вход десятого блока 4.10 формирования умножения. Значение GP с информационного выхода восьмого блока 4.8 формирования умножения поступает на второй информационный вход десятого блока 4.10 формирования умножения, с информационного выхода которого значение поступает на второй информационный вход третьего блока 5.3 формирования разности, с информационного выхода которого значение поступает на первый информационный вход шестого блока 8.6 интегрирования, с информационного выхода которого значение P поступает на первый и второй информационные входы соответственно пятого блока 4.5 и восьмого блока 4.8 формирования умножения. Значение с информационного выхода первого блока 4.1 формирования умножения поступает на второй информационный вход первого блока 5.1 формирования разности, с информационного выхода которого значение поступает на первый информационный вход первого блока 8.1 интегрирования, с информационного выхода которого значение поступает на второй информационный вход первого блока 2.1 формирования функции и на первый информационный вход второго блока 8.2 интегрирования, с информационного выхода которого значение поступает на первый и второй информационные входы соответственно первого блока 2.1 и второго блока 2.2 формирования функции. Значение с информационного выхода четвертого блока 4.4 формирования умножения поступает на первый информационный вход третьего блока 8.3 интегрирования, с информационного выхода которого снимается значение искомого вектора идентификации параметров z и подается на первый и третий информационные входы соответственно второго блока 2.2 и первого блока 2.1 формирования функции. Значение с информационного выхода второго блока 3.2 формирования производной поступает на первый информационный вход шестого блока 4.6 формирования умножения, с информационного выхода которого значение поступает на первый информационный вход первого блока 6.1 формирования суммы. Значение с информационного выхода третьего блока 3.3 формирования производной поступает на первый информационный вход седьмого блока 4.7 формирования умножения, с информационного выхода которого значение поступает на второй информационный вход первого блока 6.1 формирования суммы, с информационного выхода которого значение поступает на первый информационный вход второго блока 6.2 формирования суммы. Значение с информационного выхода четвертого блока 3.4 формирования производной поступает на второй информационный вход второго блока 6.2 формирования суммы, с информационного выхода которого значение поступает на первый информационный вход пятого блока 8.5 интегрирования, с информационного выхода которого значение поступает на второй информационный вход шестого блока 4.6 формирования умножения и на первый информационный вход четвертого блока 8.4 интегрирования, с информационного выхода которого значение G поступает на первый информационный вход второго блока 7.2 транспонирования, а также на первый и второй информационные входы соответственно восьмого блока 4.8 и седьмого блока 4.7 формирования умножения.

Первый блок интегрирования 8.1 (фиг.6) работает следующим образом. С информационного выхода первого блока 5.1 формирования разности значение поступает на первый информационный вход блока 8.1.1 формирования умножения. Значение Δt с пятого информационного выхода блока 1.1 хранения констант поступает на второй информационный вход первого 8.1 блока интегрирования, с информационного выхода которого значение поступает на первый информационный вход блока 8.1.2 формирования суммы. Значение с информационного выхода линии задержки 8.1.3 поступает на второй информационный вход блока 8.1.2 формирования суммы, с информационного выхода которого снимается значение первообразной и подается на первый вход линии задержки 8.1.3 и на второй информационный вход первого блока 2.1 формирования функции и первый информационный вход второго блока 8.2 интегрирования. Остальные блоки интегрирования работают аналогично.

Литература

1. Колесников А.А. Синергетическая теория управления. Таганрог: ТРТУ, М.: Энергоатомиздат, 1994.

2. Лурье А.И. Аналитическая механика. М.: Гос. изд-во физ.-мат. лит-ры, 1961.

3. Костоглотов А.А. Метод идентификации параметров голономных систем на основе аппарата асинхронного варьирования / Известия РАН. Теория и системы управления, 2003 г., №2. - С.86-92.

4. Датчики теплофизических и механических параметров: Справочник в 3 томах. Т.1. Под общ. ред. Ю.Н.Коптева. - М.: ИПРЖР, 1998, 458 с.

5. Андрашитов Д.С., Костоглотов А.А., Кузнецов А.А., Лазаренко С.В. Многопараметрическая идентификация конструктивных параметров методом объединенного принципа максимума // Информационный вестник Дона, 2011, http://www. ivdon.ru/magazine/latest/n1y2011/page/2/.

6. Андрашитов Д.С., Дмитренко Г.Н., Костоглотов А.А., Костоглотов А.И., Лазаренко С.В. Алгоритм идентификации параметров динамических систем. Свидетельство регистрации программ для ЭВМ. №2010616571, заявл. 05.08.10, зарегистрировано в реестре 01.10.10.

7. Андрашитов Д.С., Безуглов Д.А., Костоглотов А.А., Кузнецов А.А., Лазаренко С.В. Алгоритм многопараметрической идентификации моделей экономических систем. Свидетельство регистрации программ для ЭВМ. №2011613981, заявл. 29.03.11, зарегистрировано в реестре 23.05.11.

Устройство идентификации параметров на основе вариационных принципов содержит следующие блоки: блок хранения констант; первый, второй блоки формирования функции; первый, второй, третий, четвертый, пятый блоки формирования производной; первый, второй, третий, четвертый, пятый, шестой, седьмой, восьмой, девятый, десятый, одиннадцатый блоки формирования умножения; первый, второй, третий блоки формирования разности; первый, второй блоки формирования суммы; первый, второй блоки транспонирования; первый, второй, третий, четвертый, пятый, шестой блоки интегрирования; при этом на первый информационный вход блока хранения констант, который является входом устройства, поступает значение наблюдаемой величины; первый информационный выход блока хранения констант соединен с первым информационным входом первого блока формирования умножения; второй, третий и четвертый информационные выходы блока хранения констант соединены соответственно с первым, вторым и третьим информационными входами первого блока формирования функции; второй и четвертый информационные выходы блока хранения констант соединены соответственно со вторым и первым информационными входами второго блока формирования функции; пятый информационный выход блока хранения констант соединен со вторыми информационными входами первого, второго, третьего, четвертого, пятого и шестого блоков интегрирования; шестой информационный выход блока хранения констант соединен с первым информационным входом второго блока формирования разности; седьмой информационный выход блока хранения констант соединен с первым информационным входом второго блока формирования умножения; восьмой информационный выход блока хранения констант соединен с первым и вторым информационными входами соответственно пятого и восьмого блоков формирования умножения; девятый информационный выход блока хранения констант соединен с первым информационным входом второго блока транспонирования, а также с первым и вторым информационными входами соответственно восьмого и седьмого блоков формирования умножения; десятый информационный выход блока хранения констант соединен со вторым информационным входом шестого блока формирования умножения; одиннадцатый и двенадцатый информационные выходы блока хранения констант соединены соответственно со вторым и первым информационными входами одиннадцатого блока формирования умножения, информационный выход которого соединен с первым информационным входом третьего блока формирования разности; информационный выход первого блока формирования функции соединен соответственно с первыми информационными входами первого блока формирования разности, второго, третьего и четвертого блоков формирования производной; информационный выход второго блока формирования функции соединен с первым и вторым информационными входами соответственно первого блока транспонирования и второго блока формирования разности, информационный выход которого соединен со вторым информационным входом второго блока формирования умножения, информационный выход которого соединен со вторым информационным входом третьего блока формирования умножения; информационный выход первого блока транспонирования соединен с первым информационным входом первого блока формирования производной, информационный выход которого соединен с первым информационным входом третьего блока формирования умножения, информационный выход которого соединен соответственно со вторыми информационными входами первого и четвертого блоков формирования умножения и первым информационным входом пятого блока формирования производной, информационный выход которого соединен со вторым информационным входом девятого блока формирования умножения; информационный выход второго блока транспонирования соединен со вторым информационным входом пятого блока формирования умножения, информационный выход которого соединен соответственно с первыми информационными входами четвертого и девятого блоков формирования умножения, информационный выход которого соединен с первым информационным входом десятого блока формирования умножения; информационный выход восьмого блока формирования умножения соединен со вторым информационным входом десятого блока формирования умножения, информационный выход которого соединен со вторым информационным входом третьего блока формирования разности, информационный выход которого соединен с первым информационным входом шестого блока интегрирования, информационный выход которого соединен с первым и вторым информационными входами соответственно пятого и восьмого блоков формирования умножения; информационный выход первого блока формирования умножения соединен со вторым информационным входом первого блока формирования разности, информационный выход которого соединен с первым информационным входом первого блока интегрирования, информационный выход которого соединен со вторым информационным входом первого блока формирования функции и первым информационным входом второго блока интегрирования, информационный выход которого соединен с первым и вторым информационными входами соответственно первого и второго блоков формирования функции; информационный выход четвертого блока формирования умножения соединен с первым информационным входом третьего блока интегрирования, информационный выход которого является выходом устройства, с него же снимается значение искомого вектора идентификации параметров z и подается на первый и третий информационные входы соответственно второго и первого блоков формирования функции; информационный выход второго блока формирования производной соединен с первым информационным входом шестого блока формирования умножения, информационный выход которого соединен с первым информационным входом первого блока формирования суммы; информационный выход третьего блока формирования производной соединен с первым информационным входом седьмого блока формирования умножения, информационный выход которого соединен со вторым информационным входом первого блока формирования суммы, информационный выход которого соединен с первым информационным входом второго блока формирования суммы; информационный выход четвертого блока формирования производной соединен со вторым информационным входом второго блока формирования суммы, информационный выход которого соединен с первым информационным входом пятого блока интегрирования, информационный выход которого соединен со вторым информационным входом шестого блока формирования умножения и первым информационным входом четвертого блока интегрирования, информационный выход которого соединен с первым информационным входом второго блока транспонирования, а также с первым и вторым информационными входами соответственно восьмого и седьмого блоков формирования умножения.