Способ обработки звукового сигнала

Способ обработки звукового сигнала

Иллюстрации

Показать все

Реферат

Изобретение относится к способам обработки цифровых сигналов, в частности к сжатию сигнала и передаче огибающей спектра. Огибающая используется для квантования спектральных коэффициентов, а также участвует в распределении бит между кодируемыми полосами. Обычно огибающая спектра рассматривается как дополнительная информация при кодировании, которая должна иметь малые битовые затраты и в то же время должна передаваться с как можно меньшими потерями.

В настоящее время коммерческие системы обработки цифровых сигналов используют множество различных цифровых технологий сжатия аудиосигнала в области спектра МДКП (модифицированного дискретного косинусного преобразования). В общем случае спектр квантуется по полосам, а коэффициент усиления полосы передается как дополнительная информация. Обычно коэффициент усиления вычисляется как средняя энергия полосы, с неравномерным квантованием. Квантователь такого коэффициента, в основном, разрабатывается как квантователь по логарифмической шкале. Различные схемы кодирования используются для передачи квантованных данных, и их выбор зависит от целевой битовой скорости. Например, используется различное количество полос и различные шаги квантования. Однако для рассматриваемого кодека есть несколько ограничений на эти параметры. А именно сложность вычислений должна быть достаточно мала. Другая проблема заключается в передаче коэффициента квантования или огибающей спектра при низкой скорости кодирования. Сокращение числа полос спектра не может быть хорошим решением, хотя это и позволяет сократить битовые расходы, но неприменимо из-за ухудшения эффективности кодирования спектральных коэффициентов.

Прототипом предлагаемого изобретения является стандарт кодирования аудио G.722.1 описанный в патенте США №5924064 [1]. Данный стандарт предусматривает обработку звукового сигнала, включающую в себя преобразование временного сигнала в частотный, разбиение его на полосы, неравномерное квантование полос спектра в соответствии с квантованной энергией полос и кодирование квантов энергий и полос кодами с переменной длиной. Недостатком решения [1] является низкая эффективность кодирования квантов энергии полос.

Основная задача изобретения заключается в разработке усовершенствованного способа обработки звукового сигнала, причем такой способ должен обеспечить минимизацию битовых расходов и повышение качества квантования огибающей спектра с сохранением разрешающей способности по частоте.

Технический результат достигается за счет использования модификации границ квантов в модуле квантования значений огибающей спектра (энергий полос) и их последующего контекстного кодирования, что позволяет повысить эффективность кодирования квантов энергии полос, а также улучшает квантование энергий полос, обеспечивая, таким образом, заметное улучшение качества декодированного звука и уменьшение битовых затрат на его хранение или передачу.

Заявляемый способ обработки звукового сигнала включает в себя выполнение следующих операций:

- преобразуют временной цифровой сигнал в спектральные коэффициенты;

- извлекают огибающую спектра цифрового сигнала в виде средней энергии спектра по полосам;

- выполняют квантование огибающей и кодирование ее без потерь;

- осуществляют нормализацию спектра в соответствии с огибающей спектра по полосам и передачу нормализованного спектра;

- декодируют нормализованный спектр.

Следует отметить, что стадия кодирования в заявляемом изобретении предусматривает использование кодера и декодера. Кодирование в кодере включает в себя МДКП-преобразование, извлечение огибающей спектра, основанное на вычислении средней энергии спектральных коэффициентов в полосе, неравномерном квантовании огибающей, контекстного кодирования огибающей, нормализацию спектра и передачу нормализованного спектра. Декодирование в декодере включает в себя декодирование огибающей спектра и ее извлечение, декодирование спектральных коэффициентов и обратную нормализацию спектра соответственно огибающей, а также обратное МДКП-преобразование.

Основное преимущество заявляемого изобретения по сравнению с известными из уровня техники решениями заключается в пониженной вычислительной сложности. В частности, это объясняется тем, что, в случае, когда кодек интегрирован, он может работать одновременно с другими кодеками.

Для лучшего понимания заявляемого изобретения далее приводится его подробное описание с соответствующими чертежами.

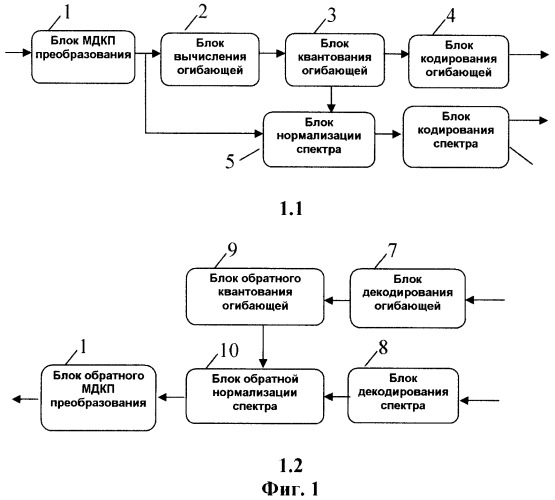
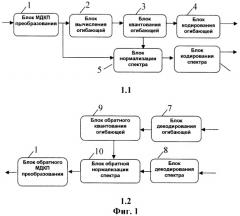
Фиг.1 - вид 1.1 - кодирование гипотетическим кодером, передающим огибающую спектра и нормированные спектральные коэффициенты;

вид 1.2 - декодирование гипотетическим кодером, использующим огибающую спектра и нормированные спектральные коэффициенты.

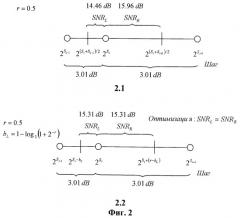
Фиг.2 - вид 2.1 - квантование логарифмической шкалой по основанию 2 и шагом 3,01 дБ (разрешение квантования 0,5);

вид 2.2 - квантование предлагаемой оптимизированной логарифмической шкалой по основанию 2 и шагом 3,01 дБ (разрешение квантования 0,5).

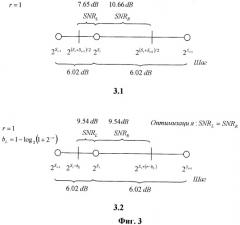
Фиг.3 - вид 3.1 - квантование логарифмической шкалой по основанию 2 и шагом 6,02 дБ (разрешение квантования 1);

вид 3.2 - квантование предлагаемой оптимизированной логарифмической шкалой по основанию 2 и шагом 6,02 дБ (разрешение квантования 1).

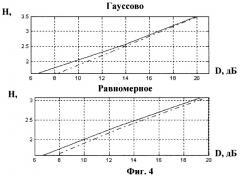
Фиг.4 - сравнительный анализ эффективности кодирования оптимизированной и не оптимизированной логарифмической шкалой квантования (по основанию 2, разрешением 0,5, 1 и 2).

Фиг.5 - типичное распределение дельт квантов огибающей, разбитых на 3 группы.

Фиг.6 - контекстное кодирование без потерь для дельт квантов огибающей, с группировкой.

Фиг.7 - распределение разности количества бит на кадр для предлагаемого алгоритма, в сравнении с оригинальным алгоритмом coding.

Фиг.8 - контекстное декодирование без потерь для дельт квантов огибающей, с группировкой.

Представленная на Фиг.1 стадия кодирования предусматривает использование кодирующего устройства и декодирующего устройства. Кодирующее устройство (вид 1.1) включает в себя блок 1 МДКП-преобразования, блок 2 вычисления огибающей, блок 3 квантования огибающей, блок 4 кодирования огибающей, блок 5 нормализации спектра, блок 6 кодирования спектра. Декодирующее устройство (вид 1.2) включает в себя блок 7 декодирования огибающей, блок 8 декодирования спектра, блок 9 обратного квантования огибающей, блок 10 обратной нормализации спектра, блок 11 обратного МДКП-преобразования.

Процесс кодирования звукового сигнала осуществляют следующим образом. Сначала выполняется прямое МДКП-преобразование временного сигнала в спектральные коэффициенты в блоке 1 МДКП-преобразования. Прямое МДКП-преобразование временного сигнала s взвешенного с окном h в спектральные коэффициенты:

где N - количество отчетов в спектре, h - окно, выбранное на основе критерия точного восстановления сигнала и степени локализации энергии, s - временной сигнал, x - спектральные коэффициенты, i и j - индексы преобразования. В частности, используют синусное окно h_j=sin[π(j+1/2)/2/N]. Коэффициенты x_i МДКП-преобразования используют в блоке 2 вычисления огибающей для расчета огибающей спектра по полосам:

где w - длина полосы спектра, x - спектральные коэффициенты, n - значение огибающей в полосе. Таким образом, огибающей n спектра МДКП-преобразования является средняя амплитуда каждой полосы. Каждое значение огибающей n спектра квантуется логарифмической шкалой в кванты n_q в блоке 3 квантования огибающей

,

где r, c, b - параметры квантования, n - значение огибающей в полосе, n_q - квант значения огибающей в полосе. Восстановленные (обратное квантование) значения применяются для нормализации спектральных коэффициентов в соответствии с огибающей спектра по полосам в блоке 5 нормализации спектра, таким образом, что средние энергии полос равняются единице. Нормализованный спектр y_i квантуется и кодируется в блоке 6 кодирования спектра с последующей передачей в битовый поток. Кодирование спектральных коэффициентов основано на методе факториального импульсного кодирования FPC (Factorial Pulse Coding), который определяет оптимальное представление полосы спектральных коэффициентов при условии минимума среднеквадратической ошибки и ограничении . Задача поиска оптимального решения решается нахождением условного экстремума при заданных ограничениях методом Лагранжа:

где L - функция Лагранжа, m - общее количество пульсов в полосе, λ - множитель Лагранжа, y_i - нормализованные коэффициенты спектра, - искомое оптимальное количество пульсов в позиции i.

Совокупность вычисленных компонентов передается в поток данных методами комбинаторного кодирования, а именно передается индекс комбинации среди всех возможных для заданной полосы. Также в поток передается информация об оптимальном множителе для минимизации ошибки квантования и выравнивания средней энергии в полосе:

где D - ошибка квантования, G - оптимальный множитель, минимизирующий ошибку квантования и выравнивающий среднюю энергию в полосе, y_i - нормализованные коэффициенты спектра, - оптимальное количество пульсов в позиции i.

Данные n_q кодируются на основе разностного кодирования (дельта кодирования) с применением контекстных моделей в блоке 4 кодирования огибающей.

Декодирование осуществляют следующим образом. Квантованная n_q огибающая спектра декодируется в блоке 7 декодирования огибающей. Спектральные коэффициенты декодируются в блоке 8 декодирования спектра, а именно по индексу вычисляется набор спектральных коэффициентов . Далее выполняется выравнивание энергии полосы спектра с помощью оптимального множителя:

где G - оптимальный множитель, минимизирующий ошибку квантования и выравнивающий среднюю энергию в полосе, - оптимальное количество пульсов в позиции i.

Обратное квантование огибающей спектра выполняется в блоке 9 обратного квантования огибающей в соответствии с формулой . Далее применяется обратная нормализация декодированных спектральных коэффициентов в блоке 10 обратной нормализации спектра, тем самым восстанавливается оригинальная энергия спектра в полосах. Далее выполняется обратное МДКП преобразование над спектральными коэффициентами в блоке 11 обратного МДКП-преобразования:

где N - количество отчетов в спектре, h - окно, выбранное на основе критерия точного восстановления сигнала и степени локализации энергии, s - временной сигнал, x - спектральные коэффициенты, i и j - индексы преобразования.

Пусть средняя амплитуда оценивается для каждой спектральной полосы. Группа средних амплитуд называется огибающей. Вычисление спектральной огибающей осуществляют по формуле:

где n - значение огибающей, w - длина полосы в отчетах, x - спектр в полосе.

Рассмотрим квантование логарифмической шкалой по основанию c. Границы квантов обозначаются аппроксимирующие точки , разрешение квантования r=S_i-S_i-1. Шаг квантования 20lg A_i-20lg A_i-1=20r lgc. Таким образом, квантование в общем случае описывается параметрически:

где b - округляющий коэффициент и в случае неоптимизированной шкалы равен r/2, с - основание логарифмической шкалы, r - разрешение квантования, n - значение огибающей в полосе, n_q - квант значения огибающей в полосе.

Обратное квантование огибающей выполняется согласно формуле:

,

где c - основание логарифмической шкалы, r - разрешение квантования,

n_q - значение кванта, - восстановленное значение огибающей.

В случае неоптимизированной шкалы левая и правая границы кванта отстоят от аппроксимирующей точки на разные расстояния. Данная разница приводит к разным значениям максимально возможной ошибки квантования данных SNR, как показано на Фиг.2, вид 2.1 (шаг квантования 3,01 дБ), и Фиг.3, вид 3.1 (шаг квантования 6,02 дБ), при квантуемых значениях, лежащих на границах кванта.

Главная идея предлагаемой шкалы квантования состоит в изменении границ квантов таким образом, чтобы максимальная возможная ошибка (SNR) внутри каждого кванта была наименьшей. Максимальная ошибка (SNR) внутри кванта будет наименьшей в том случае, если ошибки квантования значений, попавших на левую и правую границы кванта, будут идентичны. Изменение границ квантов может быть выражено через изменение округляющего коэффициента b.

Характеристика SNR для левой и правой границ кванта вычисляется как:

где c - основание логарифмической шкалы, s_i - показатель степени на границе кванта i, SNR_L и SNR_R - SNR-характеристика для левой и правой границы кванта соответственно.

Пусть смещение показателей степени аппроксимирующей точки от левой и правой границы кванта обозначается через параметры b_L и b_r:

где S_i - показатель степени на границе кванта i, b_L и b_R - смещения показателей степени аппроксимирующей точки от левой и правой границы кванта соответственно.

Очевидно, что сумма смещений показателей степени для левой b_L и правой границы b_r равна разрешению квантования:

где r - разрешение квантования, b_L и b_R - смещения показателей степени аппроксимирующей точки от левой и правой границы кванта соответственно.

Также, исходя из общих свойств квантования, округляющий коэффициент в точности равен смещению показателя степени для левой границы кванта. Таким образом, подстановка выражения (5) в выражение (4) позволяет вычислить SNR для левой и правой границы через параметр b_L:

где c - основание логарифмической шкалы, S_i - показатель степени на границе кванта i, SNR_L и SNR_R - SNR-характеристика для левой и правой границы кванта соответственно, b_L и b_R - смещения показателей степени аппроксимирующей точки от левой и правой границы кванта; соответственно, r - разрешение квантования.

Приравнивание SNR для левой и правой границы кванта позволяет определить параметр b_L:

.

где c - основание логарифмической шкалы, b_L - смещение показателя степени аппроксимирующей точки от левой границы кванта и численно равное оптимальному округляющему коэффициенту b, r - разрешение квантования.

Таким образом, округляющий коэффициент равен:

где r - разрешение квантования, с - основание логарифмической шкалы, b_L - оптимальный округляющий коэффициент.

Предложенная логарифмическая шкала квантования с шагом квантования 3,01 дБ (основание логарифма 2) и разрешением квантования 0,5 приведена на Фиг.2, вид 2.2. Разница ошибки квантования SNR между левой и правой границей идентична и равна 15,31 дБ. Предложенная логарифмическая шкала квантования с шагом квантования 6,02 дБ (основание логарифма 2) и разрешением квантования 1,0 приведена на Фиг.3, вид 3.2. Разница ошибки квантования SNR между левой и правой границей идентична и равна 9,54 дБ. Округляющий коэффициент b=b_L определяет расстояние в показатели степени между аппроксимирующей точкой и левой и правой границами квантов. Таким образом, квантование выполняется по следующей формуле:

где r - разрешение квантования, c - основание логарифмической шкалы, n - значение огибающей в полосе, n_q - квант значения огибающей в полосе, b_L - оптимальный округляющий коэффициент, определенный по формуле (7).

Экспериментальные результаты для квантования логарифмической шкалой с основанием 2 приведены на Фиг.4. Из теории информации известно, что критерием для сравнительного анализа различных способов квантования является функция скорость-искажение H(D). За скорость кодирования принята энтропия набора квантов и имеет размерность бит/отчет, в качестве меры искажения принята среднеквадратическая ошибка (SNR). Сплошная линия на Фиг.4 соответствует функции скорость-искажение для неоптимизированной логарифмической шкалы квантования, пунктирная линия - функции скорость-искажение для предложенной оптимизированной логарифмической шкалы квантования. Отчеты гауссова и равномерного распределения сгенерированы датчиком случайных чисел с соответствующим законом распределения, нулевым математическим ожиданием и единичной дисперсией. Функция скорость-искажение H(D) вычисляется при последовательном изменении разрешения квантования. На Фиг.4 видно, что пунктирная линия располагается ниже сплошной линии, что означает: предложенная оптимизированная логарифмическая шкала квантования лучше неоптимизированной логарифмической шкалы квантования в терминах критерия H(D).

Иными словами, для одной и той же скорости кодирования предложенная шкала позволяет квантовать с меньшей ошибкой или при одной и той же ошибке квантования предложенная шкала позволяет передавать информацию меньшим количеством бит. Экспериментальные результаты приведены в Таблице 1 для неоптимизированной логарифмической шкалы квантования и Таблице 2 для предложенной оптимизированной логарифмической шкалы квантования.

Таблица 1
Разрешение квантования r	2,0	1,0	0,5
Округляющий коэффициент b/r	0,5	0,5	0,5
Гауссово распределение
Скорость H, b/s	1,6179	2,5440	3,5059
Ошибка D, дБ	6,6442	13,8439	19,9534
Равномерное распределение
Скорость H, b/s	1,6080	2,3227	3,0830
Ошибка D, дБ	6,6470	12,5018	19,3640

Таблица 2
Разрешение квантования r	2,0	1,0	0,5
Округляющий коэффициент b/r	0,3390	0,4150	0,4569
Гауссово распределение
Скорость H, b/s	1,6069	2,5446	3,5059
Ошибка D, дБ	8,2404	14,2284	20,0495
Равномерное распределение
Скорость H, b/s	1,6345	2,3016	3,0449
Ошибка D, дБ	7,9208	12,8954	19,4922

Данные таблицы 1 и 2 показывают, что для разрешения квантования 0,5 характеристика SNR улучшена на 0,1 дБ, для разрешения квантования 1,0 характеристика SNR улучшена на 0,45 дБ, а для разрешения квантования 2,0 характеристика SNR улучшена на 1,5 дБ.

Предложенный способ квантования не увеличивает сложность, так как меняется только таблица поиска квантованного значения, которая зависит от округляющего коэффициента (7).

Контекстное кодирование огибающей основано на дельта-кодировании. Изначально вычисляется разность между следующим и текущим значением огибающей:

где d(i) - это дельта для значения i+1, n_q(i) - значение огибающей в полосе i, n_q(i+1) - это значение огибающей в полосе i+1.

Полученные разности d(i) ограничиваются диапазоном [-15, 16].

Это обеспечивается путем регулирования сначала отрицательных индексов, а затем положительных, как описано ниже:

- вычисляют разность согласно выражению (9), начиная от высокочастотных полос и заканчивая низкочастотными;

- если d(i)<-15, то n_q(i)=n_q(i+1)+15, i=42, …,0;

- пересчитывают разность, начиная от низкочастотных полос и заканчивая высокочастотными;

- если d(i)>16, d(i)=16 и n_q(i+1)=n_q(i)+16, i=0, …,42;

- для перевода разностных индексов в диапазон [0, 31], добавляют ко всем значениям d(i) смещение 15.

Первое значение обычно кодируется «как есть», так как оно используется в качестве базового для дельта-кодирования. Однако для получения лучшего сжатия можно использовать дельта-кодирование, где в качестве опорного значения используется некоторая константа, например среднее по большой выборке значение огибающей в первой полосе. Дельты d(i) кодируются с использованием контекстной модели. Используется модификация с несколькими кодами Хаффмана, код выбирается в зависимости от контекста. Из-за ограничения на алгоритм кодирования, которое не позволяет использовать любые данные из предыдущего кадра, в качестве контекста может выступать только значение предыдущей дельты на текущем кадре.

В результате анализа распределения вероятностей дельт квантов было определено, что можно выделить несколько различных моделей распределения, поэтому была выполнена группировка квантов, имеющих сходные модели распределения. Параметры групп и их количество были определены при помощи симулирования на языке Matlab, для получения наилучшего сжатия, но с учетом ограничения, что битовые потери относительно неограниченного количества групп не превысят 0,5%.

Параметры групп приведены в Таблице 3.

Таблица 3
Номер группы	Нижняя граница дельты	Верхняя граница дельты
#1	0	12
#2	13	17
#3	18	31

Распределение вероятностей в группах показано на Фиг 5. Легко видеть, что распределения для групп #1 и #3 похожи, но инвертированы по оси x. Это означает, что всего один код может быть использован для обеих групп без каких бы то ни было существенных потерь в эффективности кодирования. Для этого индекс кодового слова должен отсчитываться в обратном порядке для группы #3.

Схема кодера с тремя группами с контекстом в виде предыдущего значения дельты и двумя различными кодами Хаффмана предложена на Фиг.6. Анализ разности битовых затрат по кадрам приведен в Таблице 4. Эффективность кодирования увеличилась в среднем на 9% по сравнению с оригинальным алгоритмом.

Таблица 4
Алгоритм	Битовая скорость, kbps	Выигрыш, %
Кодирование Хаффмана	6,25	-
Контекст + Хаффман	5,7	9%

Алгоритм декодирования работает аналогично кодеру, в качестве контекста используется предыдущее значение декодированной дельты 3.01 dB, как показано на Фиг.8.

Заявленный способ может найти применение в современных системах обработки цифровых сигналов, обеспечивая повышенную эффективность кодирования квантов энергии полос, а также улучшение квантования энергий полос, что дает заметное улучшение качества декодированного звука и уменьшение битовых затрат на его хранение или передачу.

1. Способ обработки звукового сигнала, включающий: преобразование временного сигнала в спектральные коэффициенты, извлечение огибающей спектра сигнала в виде средней энергии спектра по полосам, квантование огибающей и кодирование ее без потерь, нормализацию спектра в соответствии с огибающей спектра по полосам и передачу нормализованного спектра с последующим декодированием.

2. Способ по п.1, отличающийся тем, что извлечение огибающей спектра сигнала выполняют на основе вычисления средней энергии спектральных коэффициентов в полосе.

3. Способ по п.1, отличающийся тем, что в процессе нормализации спектра в соответствии с огибающей спектра выполняют приведение средней энергии полос спектра к единице.

4. Способ по п.1, отличающийся тем, что нормализованный спектр квантуют и кодируют с последующей передачей в битовый поток.

5. Способ по п.1, отличающийся тем, что для преобразования временного сигнала в спектральные коэффициенты используют МДКП-преобразование.

6. Способ по п.1, отличающийся тем, что квантование производят с использованием скалярного квантования с минимизацией искажений.

7. Способ по п.1, отличающийся тем, что границы квантов огибающей равноудалены от точки приближения, с точки зрения искажения.

8. Способ по п.1, отличающийся тем, что квантование огибающей осуществляют на основе логарифмической функции.

9. Способ по п.1, отличающийся тем, что при квантовании огибающей используют оптимальный округляющий коэффициент, с точки зрения искажения.

10. Способ по п.1, отличающийся тем, что при кодировании огибающей без потерь используют контекстное кодирование, где ранее закодированные значения используют в качестве контекста.

11. Способ по п.10, отличающийся тем, что ранее закодированные значения группируют и номер группы используют в качестве контекста.

12. Способ по п.1, отличающийся тем, что в процессе декодирования выполняют следующие операции: декодируют огибающую спектра без потерь, деквантуют огибающую, декодируют спектр, проводят обратную нормализацию спектра при помощи огибающей и преобразования спектральных коэффициентов во временной сигнал.

13. Способ по п.12, отличающийся тем, что в процессе обратной нормализации применяют восстановление энергии полос спектра, равной значениям огибающей в соответствующих полосах.

14. Способ по п.12, отличающийся тем, что для преобразования спектральных коэффициентов во временной сигнал используют обратное МДКП-преобразование.

15. Способ по п.12, отличающийся тем, что деквантование выполняют с помощью скалярного деквантователя с минимизацией искажений.

16. Способ по п.12, отличающийся тем, что в деквантователе огибающей границы квантов равноудалены от точки приближения, с точки зрения искажения.

17. Способ по п.12, отличающийся тем, что деквантование огибающей реализуют на основе логарифмической функции.

18. Способ по п.12, отличающийся тем, что при деквантовании огибающей используют оптимальный округляющий коэффициент, с позиции искажений.

19. Способ по п.12, отличающийся тем, что при декодировании огибающей без потерь используют контекстное декодирование, где ранее декодированные значения используют в качестве контекста.

20. Способ по п.19, отличающийся тем, что ранее декодированные значения группируют и группу используют в качестве контекста.