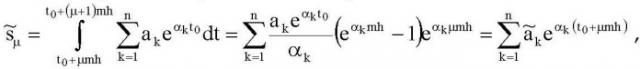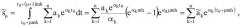Способ и устройство для аппроксимации сигналов

Способ и устройство для аппроксимации сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к области цифровой обработки сигналов и информационно-измерительной техники и может быть использовано для линеаризации функции преобразования блоков и систем, интерполяции и экстраполяции результатов измерений, сжатия и восстановления сигналов, а также для измерения параметров сигналов сложной формы, а именно параметров колебательных компонент сигнала.

Известны и широко применяются способы и реализующие их устройства для полиноминальной, сплайновой и Фурье-аппроксимации сигналов [1, 2, 3]. Их основным недостатком является низкая точность аппроксимации знакопеременных сигналов и значительное влияние случайных шумов, неизбежно наложенных на сигнал, и шумов квантования (оцифровки) на получаемые результаты. Известен также способ аппроксимации линейными комбинациями экспонент, основанный на применении метода наименьших квадратов [3], и устройство для его реализации [4]. Недостатком этого способа является трудоемкость расчетов параметров аппроксимирующего агрегата, затрудняющая его реализацию на микроконтроллерах, и использование в составе мобильных систем в реальном времени.

Из известных способов аппроксимации наиболее близким по технической сущности является способ интерполяции экспоненциальными суммами, основанный на алгоритме частных и разностей (Рутисхаузер Г. Алгоритм частных и разностей. - М.: Изд-во иностр. литер. 1960. - 93 с. [5], стр.54-60).

В этом способе задают число n экспонент, используемых для аппроксимации, непрерывную функцию дискретизируют с постоянным шагом дискретизации h, равным длине промежутка аппроксимации, деленной на 2n-1, и вычисляют на основе алгоритма частных и разностей по полученным дискретным значениям параметры экспонент.

В способе-прототипе для аппроксимации непрерывной функции F(t) используется сумма экспонент (конечная сумма Дирихле) вида

совпадающая с функцией F(t) в 2n точках t_ν=t₀+νh, ν=0, 1,…, 2n-1, заданных с постоянным шагом дискретизации h. Задача сводится к представлению в виде суммы простейших дробей рациональной функции f(z), представляющей z-преобразование исходной функции F(t), для которой

ν=0, 1,…, 2n-1.

Тогда [5, с.54]

где , .

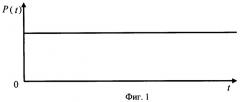
На фиг.1, 2, 3 и 4 представлены формы отдельных компонент аппроксимирующей функции F(t_ν) при различных видах α_k. Так как исходные данные для аппроксимации - значения функции F(t) являются действительными числами, то a _k и α_k могут быть как действительными числами, так и встречаться комплексно-сопряженными парами a _k, и α_k, . Если α_k=0, то компонента представляет собой постоянное напряжение, изображенное на фиг.1. Если α_k - действительное число, то компонента представляет собой экспоненту, изображенную на фиг.2. Если действительные части комплексно-сопряженной пары α_k, равны нулю, то компонента представляет собой гармоническое колебание, изображенное на фиг.3. Если действительные части комплексно-сопряженной пары α_k, не равны нулю, то соответствующая им компонента сигнала представляет собой затухающее гармоническое колебание, изображенное на фиг.4. Вид a _k влияет только на фазу гармонического колебания.

Известный способ реализует следующую последовательность действий.

1. Исходя из априори известных характера функции и требуемой точности аппроксимации, задают порядок аппроксимирующей модели, то есть число n экспонент, используемых для аппроксимации.

2. Непрерывную функцию F(t) дискретизируют с постоянным шагом дискретизации h, то есть представляют ее последовательностью , содержащей 2n дискретных цифровых значений F(t_ν)=s_ν.

3. Применяют алгоритм частных и разностей для определения параметров экспонент следующим образом.

3.1. По значениям s_ν вычисляют частные и разности , σ=1, 2,…, c помощью правил ромба [5, с.13]

при условии, что , ν=0, 1,…,2n, а все числа равны нулю.

3.2. Находят последовательности и , а все полагают равными нулю.

3.3.Определяют полюсы функции f(z) по найденным в п.3.2 последовательностям с помощью прогрессивной формы алгоритма частных и разностей [5, стр.37-41,43-53], считая все равными нулю,

3.4. Находят по результатам п.п.3.2 и 3.3 коэффициенты в разложении функции f(z) на простейшие дроби с помощью модификаций алгоритма частных и разностей [5, стр.28-31, стр.57-60].

4. Вычисляют по полученным значениям и искомые параметры аппроксимирующего агрегата α_k=h^-1ln(λ_k) и , k=1,…, n.

В результате аппроксимирующая функция, описываемая линейной комбинацией экспонент, в 2n точках совпадает с исходной непрерывной функцией F(t).

Недостатком способа-прототипа при его практической реализации является низкая точность аппроксимации сигналов, обусловленная тем, что количество отсчетов аппроксимируемого сигнала фиксировано априори. При малом числе отсчетов погрешность аппроксимации в промежуточных точках исходной функции F(t), описывающей сигнал, велика, а при большом числе отсчетов возникает неоправданное усложнение вычислений и проявляется неустойчивость алгоритма частных и разностей. Кроме того, реальные сигналы неизбежно сопровождаются наложенными на них шумами и при оцифровке сигналов возникают шумы квантования. Это также приводит к снижению точности аппроксимации, так как аппроксимирующая функция совпадает в точках аппроксимации с сигналом с наложенными на него шумами, а в ряде случаев к неустойчивости алгоритма и невозможности аппроксимации.

Целью предлагаемого изобретения является повышение точности аппроксимации при практической реализации способа для реальных сигналов.

Указанная цель достигается тем, что в способе аппроксимации непрерывных сигналов конечной линейной комбинацией экспонент, включающем дискретизацию, оцифровку сигнала и вычисление по полученным значениям параметров экспонент на основе алгоритма частных и разностей, предварительно производят разбиение дискретных отсчетов сигнала на М блоков равной длительности, проводят численное интегрирование сигнала в каждом блоке, вычисляют параметры экспонент, аппроксимирующих интегрированный сигнал, по ним рассчитывают параметры экспонент, аппроксимирующих сигнал, число блоков М выбирают равным или большим удвоенного числа экспонент, используемых для аппроксимации, а необходимое число экспонент определяют априори и уточняют в процессе выполнения алгоритма частных и разностей.

В заявляемом способе для аппроксимации непрерывного сигнала F(t) также используется сумма экспонент (конечная сумма Дирихле) вида

совпадающая с исходным сигналом F(t) в 2n точках t_ν=t₀+νh, ν=0, 1,…, 2n-1, заданных с постоянным шагом дискретизации h. Для этого сигнал F(t) дискретизируют и оцифровывают, представляя его N отсчетами сигнала , сигнала F(t) в моменты времени t₀, t₁,…, t_N-1, t_ν=t₀+νh, ν=0, 1,…, N-1, причем N>>2n. Отсчеты сигнала разбивают на М одинаковых блоков , , число которых не меньше удвоенного числа экспонент, а N-1=Mm. Интегрирование P(t) по интервалу [t₀+µmh, t₀+(µ+1)mh], где µ=0,…, M-1, дает

µ=0,…, M-1.

То есть исходный интервал дискретизации h заменяется большим интервалом дискретизации mh.

По найденным отсчетам интегрированного сигнала находим z-преобразование этого сигнала

где , .

Применение алгоритма частных и разностей к последовательности позволяет вычислить полюсы и коэффициенты разложения на простейшие дроби, по которым определяют параметры аппроксимирующего агрегата

и , k=1,…, r.

Число r экспонент, используемых для аппроксимации, не превышает целой части числа М/2 и определяется в процессе выполнения алгоритма частных и разностей из условия: меньше наперед заданной погрешности.

Предлагаемый способ реализует следующую последовательность действий.

1. Непрерывный сигнал F(t) дискретизируют и оцифровывают с постоянным шагом дискретизации h, то есть представляют его N отсчетами в моменты времени t₀, t₁,…, t_N-1, t_ν=t₀+νh, ν=0, 1,…, N-1, причем число отсчетов N много больше удвоенного числа требуемых для аппроксимации экспонент.

2. Исходя из априори известных характера сигнала, требуемой точности аппроксимации и числа отсчетов N, выбирают число М, которое не меньше удвоенного числа экспонент, требуемых для аппроксимации.

3. Отсчеты сигнала разбивают на М одинаковых блоков, длительностью m

, , а N-1=Mm.

4. Проводят численное интегрирование дискретизированного сигнала в каждом из М блоков и получают новую последовательность интегрированных значений .

5. Применяют алгоритм частных и разностей для определения параметров экспонент следующим образом.

5.1. По значениям вычисляют частные и разности , k=1, 2,…, с помощью правил ромба

при условии, что , µ=0, 1…, M-1, а все числа равны нулю.

5.2. Находят последовательности и , где r не превышает целой части числа М/2 и определяется в процессе выполнения алгоритма частных и разностей из условия: меньше наперед заданной погрешности. Число r ограничивает количество экспонент, необходимых для аппроксимации сигнала с заданной погрешностью.

5.3. Полагают равным нулю и по найденным в п.5.2 последовательностям и определяют полюсы функции .

5.4. Находят по результатам п.п.5.2 и 5.3 коэффициенты в разложении функции на простейшие дроби.

6. Вычисляют по полученным значениям и искомые параметры аппроксимирующего агрегата и k=1,…, r.

6.1. При измерении параметры колебательных компонент сигнала - частоты f_k [Гц], коэффициенты затухания β_k [с^-1], амплитуды A_k [В] и начальные фазы θ_k [рад] - вычисляют по полученным значениям α_k и a _k, соответственно:

f_k=(2π)^-1Im(α_k), β_k=Re(α_k),

,

или непосредственно по значениям и :

Технический результат - повышение точности аппроксимации сигналов достигается за счет интегрирования дискретных отсчетов сигнала в пределах М блоков, при этом случайные шумы усредняются, а также за счет выбора числа экспонент, используемых для аппроксимации, непосредственно в процессе реализации способа, исходя из допустимой погрешности.

Технический результат достигается также за счет применения нового устройства для реализации заявленного способа аппроксимации сигналов, содержащего аналого-цифровой преобразователь, интегратор, блок вычисления последовательностей частных и разностей и блок вычисления параметров аппроксимирующего агрегата, соединенные последовательно, а также блок задания интервалов интегрирования, выход которого подключен к управляющему входу интегратора, и пороговую схему, вход которой соединен с выходом блока вычисления последовательностей частных и разностей, а выход подключен к управляющему входу блока вычисления последовательностей частных и разностей.

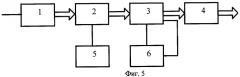
На фиг.5 приведена функциональная схема устройства, реализующего заявляемый способ аппроксимации сигналов.

Устройство для аппроксимации сигналов содержит аналого-цифровой преобразователь 1, интегратор 2, блок 3 вычисления последовательностей частных и разностей, блок 4 вычисления параметров α_k и a _k аппроксимирующего агрегата, блок 5 задания интервалов интегрирования и пороговую схему 6. Аналого-цифровой преобразователь 1, интегратор 2, блок 3 вычисления последовательностей частных и разностей и блок 4 вычисления параметров α_k и a _k аппроксимирующего агрегата соединены последовательно. Выход блока 5 задания интервалов интегрирования соединен с управляющим входом интегратора 2. Вход пороговой схемы 6 подключен к выходу блока 3 вычисления последовательностей частных и разностей, а его выход - к управляющему входу блока 3 вычисления последовательностей частных и разностей.

Все элементы, входящие в состав устройства, могут быть реализованы в виде отдельных функциональных узлов, например блоки 2-6 на программируемых логических интегральных схемах (ПЛИС) или программным способом при использовании микроконтроллера, оснащенного аналого-цифровым преобразователем.

Работает устройство для аппроксимации сигналов следующим образом. Аналого-цифровой преобразователь 1 осуществляет дискретизацию и оцифровку аппроксимируемого непрерывного сигнала F(t), преобразуя его в последовательность N цифровых отсчетов в моменты времени t₀, t₁,…, t_N-1, t_ν=t₀+νh, ν=0, 1,…, N-1. Частота дискретизации высокая и определяется возможностями аналого-цифрового преобразователя 1. В интеграторе 2 выполняется численное интегрирование дискретизированного сигнала на интервалах времени М, задаваемых блоком 5 задания интервалов интегрирования. Число интервалов М устанавливается до начала работы не меньшим, чем удвоенное число экспонент, требуемых для аппроксимации сигнала с заданной точностью, и зависит от ожидаемого характера сигнала F(t). Последовательность интегрированных значений сигнала , где µ=0,…, М-1, поступает в блок 3 вычисления последовательностей частных и разностей, где с использованием алгоритма частных и разностей вычисляют частные и разности , k=1, 2,…, по которым находят последовательности и . В процессе вычисления этих последовательностей каждое очередное значение сравнивается пороговой схемой 6 с наперед заданной погрешностью ε. Если очередное значение становится меньше ε, вычисление прекращается. Если это условие не достигается, то вычисление прекращается, когда число членов последовательности становится равным целой части M/2. В блоке 4 вычисления параметров аппроксимирующего агрегата по значениям , определяют полюсы функции , находят коэффициенты в разложении функции на простейшие дроби и вычисляют искомые параметры аппроксимирующего агрегата по следующим формулам

и , k=1,…, r.

Моделирование известного и предлагаемого способов аппроксимации в среде «MAPLE» показало, что при использовании точных значений сигнала среднее квадратичное отклонение аппроксимирующей функции от сигнала для обоих способов не превышает сотых долей процента. При использовании квантованных значений сигнала с четырьмя десятичными разрядами в качестве исходных данных для аппроксимации в известном способе проявляется неустойчивость алгоритма и в ряде случаев аппроксимации не возможна, в то время как в предлагаемом способе среднее квадратичное отклонение аппроксимирующей функции от сигнала не превышает десятых долей процента. При наложении на аппроксимируемый сигнал нормального шума с отношением сигнал/шум до 500 и использовании оцифрованных значений сигнала с четырьмя десятичными разрядами в качестве исходных данных для аппроксимации известный способ практически перестает работать, в то время как предлагаемый способ сохраняет то же значение среднего квадратичного отклонения аппроксимирующей функции от сигнала. Известный способ аппроксимации не работает, если число отсчетов сигнала превышает число точек аппроксимации.

Предлагаемое изобретение может быть применено для решения различных задач информационно-измерительной техники. Параметры аппроксимирующего агрегата α_k и a _k могут быть применены для расчетов поправочных коэффициентов при линеаризации функций преобразования. В задачах сжатия-восстановления сигналов по каналам телеметрии целесообразно передавать или последовательности частных и разностей , или параметры аппроксимирующего агрегата α_k и a _k. Объем передаваемой информации при этом не изменяется. Восстановление сигнала может проводиться как по параметрам аппроксимирующего агрегата α_k и a _k, рассчитанным на приемной стороне, так и по параметрам (частотам, амплитудам, начальным фазам и коэффициентам затухания) колебательных компонент сигнала.

Использованные источники

1. Попов Б.А., Теслер Г.С. Вычисление функций на ЭВМ. Справочник. - Киев: Наукова думка, 1984. - 600 с.

2. Патент RU 2010324, G06F 15/31. Устройство для аппроксимации функций. Опубл. 30.03.1994 г.

3. Марпл.-мл. С.Л. Цифровой спектральный анализ и его приложения: Пер. с англ. - М.: Мир, 1990. - 584 с.

4. Ионов С.В., Мясникова М.Г., Цыпин Б.В., Шаповал И.О. Модульная система для измерения параметров и спектрального анализа слабых сигналов // Измерительная техника. - 2011. - №4.

5. Рутисхаузер Г. Алгоритм частных и разностей. - М.: Изд-во иностр. литер., 1960. - 93 с.

1. Способ аппроксимации непрерывных сигналов конечной линейной комбинацией экспонент, включающий дискретизацию, оцифровку сигнала и вычисление по полученным значениям параметров экспонент на основе алгоритма частных и разностей, отличающийся тем, что предварительно производят разбиение дискретных отсчетов сигнала на М блоков равной длительности, проводят численное интегрирование сигнала в каждом блоке, вычисляют параметры экспонент, аппроксимирующих интегрированный сигнал, а по ним рассчитывают параметры экспонент, аппроксимирующих сигнал.

2. Способ по п.1, отличающийся тем, что число блоков М выбирают равным или большим необходимого для аппроксимации удвоенного числа экспонент, а необходимое число экспонент определяют в процессе выполнения алгоритма частных и разностей.

3. Устройство для аппроксимации сигналов, содержащее аналого-цифровой преобразователь, интегратор, блок вычисления последовательностей частных и разностей и блок вычисления параметров аппроксимирующего агрегата, соединенные последовательно, а также блок задания интервалов интегрирования, выход которого подключен к управляющему входу интегратора, и пороговую схему, вход которой соединен с выходом блока вычисления последовательностей частных и разностей, а выход подключен к управляющему входу блока вычисления последовательностей частных и разностей.