Способ линеаризации градуировочной характеристики измерительного преобразователя

Способ линеаризации градуировочной характеристики измерительного преобразователя

Иллюстрации

Показать все

Реферат

Изобретение относится к измерительной технике и может быть использовано для линеаризации градуировочных характеристик любых измерительных преобразователей, у которых градуировочная характеристика аппроксимируется полиномом второго порядка.

Градуировочная характеристика (ГХ) - это зависимость между значениями величин на входе и выходе измерительного преобразователя (ИП), полученная экспериментально. У многих ИП полученные ГХ могут быть аппроксимированы полиномом второго порядка с достаточно большой точностью. Необходимо линеаризовать такие ГХ, т.е. аппроксимировать (приблизить) ГХ прямой.

Известен способ линеаризации градуировочной характеристики пьезорезонансного ИП с переменным межэлектродным зазором (патент RU №2127496, МПК H04R 17/00, заявл. 18.01.1996, опубл. 10.03.1999), заключающийся в следующем. Сигнал первичного преобразователя пьезорезонансного частотного измерительного преобразователя гетеродинируют. Получают линеаризованную градуировочную характеристику последнего. Определяют номинальную частоту с первичного преобразователя, равную резонансной частоте пьезорезонатора с двумя электродами, находящимися непосредственно на обеих поверхностях пьезоэлемента, определяют частотную градуировочную характеристику и, аппроксимируя ее дробно-линейной функцией вида, устанавливают частоту гетеродина. Для определения частотной градуировочной характеристики используют функцию преобразования первичного измерительного преобразователя, снятую предварительно. Технический результат - повышение линейности градуировочной характеристики частотного измерительного преобразователя. Недостатком данного способа является специфичность используемых операций для повышения линейности градуировочной характеристики пьезорезонансного ИП и соответственно невозможность применения данного способа для других типов ИП.

Наиболее распространенным способом приближения полинома второго порядка прямой (линеаризации) с определенной погрешностью приближения является метод наименьших квадратов (МНК) (МИ 2175-91. ГСИ. Градуировочные характеристики средств измерений. Методы построения, оценивание погрешностей, или Кочетков, Е.С. Метод наименьших квадратов: Учеб. пособие / Е.С.Кочетков. - М.: Изд-во МАИ, 1993. - 43 с.). Данный метод основан на формировании ряда эталонных сигналов, значения которых равноудалены по диапазону изменения измеряемого сигнала. По выходным сигналам ИП, полученным от преобразования эталонных сигналов, определяют прямую, имеющую минимальное среднеквадратичное отклонение от этих выходных сигналов. Недостатком этого метода является интегральность критерия оптимальности, т.е. данный метод оптимален при минимальности средней погрешности линеаризации на диапазоне измерения, но не оптимален к минимуму максимальной погрешности линеаризации. А ведь практически все ИП имеют нормируемые характеристики в виде предельных значений, а не средних.

Наиболее близким по технической сущности к заявляемому способу является способ, основанный на наилучшем равномерном приближении (Бахвалов, Н.С. Численные методы / Н.С.Бахвалов, Н.П.Жидков, Г.М.Кобельков. - 4-е изд. - М.: БИНОМ. Лаборатория знаний, 2006. - 636 с.). Способ основан на использовании функции Чебышева второго порядка:

T₂(x)=2x²-1,

где x∈[-1,1]. Максимальные отклонения этой функции от нуля отличаются по знаку и равны по величине. Значения x₁, x₂, при которых функция T₂(x) равна нулю, (нули функции) равны:

;

.

При x∈[а,b], где а и b - нижняя и верхняя границы диапазона изменения измеряемой величины:

Способ заключается в формировании двух эталонных сигналов, значения которых не зависят от задаваемого предела погрешности линеаризации и равны (1), (2). Эталонные сигналы последовательно подаются на ИП, и выходные сигналы ИП, полученные от преобразования эталонных сигналов, регистрируются. По двум зарегистрированным выходным сигналам ИП и значениям эталонных сигналов определяют прямую. Получившиеся максимальные отклонения ГХ ИП от прямой будут разными по знаку и равными по значению, т.е. получается минимально возможная максимальная погрешность линеаризации.

Недостатком данного метода является необходимость задания предела погрешности линеаризации ГХ ИП в виде постоянного значения, а ведь многие ИП имеют предел абсолютной погрешности измерения и, соответственно, предел абсолютной погрешности аппроксимации Δ_a в виде значения, пропорционального измеряемой величине x:

Δ_a=d+cx,

где d и с - некоторые постоянные. Применение оптимального равномерного приближения в этом случае приведет к необходимости выполнять более жесткие требования:

Δ_a=d,

так как равномерное приближение обеспечивает максимальную погрешность линеаризации, одинаковую на всем диапазоне изменения измеряемой величины. Это может привести к невозможности линеаризовать ГХ с заданной погрешностью.

В основу предлагаемого изобретения положена техническая задача, заключающаяся в оптимальном распределении погрешности линеаризации градуировочных характеристик измерительных преобразователей по диапазону изменения измеряемой величины при задании предела погрешности линеаризации в виде значения, пропорционального измеряемой величине.

Указанная задача решается тем, что способ линеаризации градуировочной характеристики измерительного преобразователя, аппроксимируемой полиномом второго порядка, включающий формирование двух эталонных сигналов, последовательную подачу эталонных сигналов на вход измерительного преобразователя (ИП), регистрацию выходных сигналов ИП, определение прямой по двум зарегистрированным выходным сигналам ИП и значениям эталонных сигналов, задание предела абсолютной погрешности линеаризации в виде значения, пропорционального измеряемой величине:

Δ_a=d+cx,

где Δ_a - предел абсолютной погрешности линеаризации; d и с - постоянные; x - измеряемая величина, характеризуется тем, что формируют значения двух эталонных сигналов зависящими от предела погрешности линеаризации и равными:

где x₁, x₂ - значения эталонных сигналов; а и b - нижняя и верхняя границы диапазона изменения измеряемой величины;

;

.

Введение в предлагаемый способ линеаризации ГХ ИП операции по формированию значений эталонных сигналов, зависящих от задаваемого предела погрешности линеаризации ГХ, позволяет оптимально распределить погрешность линеаризации ГХ ИП по диапазону изменения измеряемой величины при задании предела абсолютной погрешности линеаризации в виде значения, пропорционального измеряемой величине.

Изобретение основано на введении функции второго порядка L₂(x), x∈[-1,1], для оптимального пропорционального приближения:

L₂(x)=a₀+a₁х+a₂х².

Если задать предел абсолютной погрешности линеаризации в следующем виде:

,

где k=c/d, то условия для определения коэффициентов а₀, а₁, а₂:

где x_min - значение переменной x, при которой L₂(x) имеет минимальное значение. Значение x_min находится из условия равенства нулю :

.

Решая систему из трех уравнений (6), получаем:

;

;

.

Для проверки при k=0:

L₂(x)=2x²-1=T₂(x),

где Т₂(x) - функция Чебышева второго порядка. При x∈[а,b] нулями функции L₂(x) будут значения (3), (4).

Работа способа линеаризации ГХ ИП рассмотрена на примере ИП, предназначенного для измерения напряжения в диапазоне от 0 до 100 мВ с пределом абсолютной погрешности аппроксимации Δ_а, мВ:

где x - измеряемое напряжение, мВ. ГХ данного ИП аппроксимируется полиномом Р₂(x), мВ:

P₂(x)=1,4x-4·10^-3x².

Изобретение иллюстрируется фиг.1-5, где представлены:

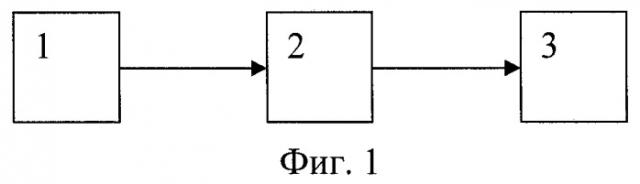
на фиг.1 - функциональная схема устройства для линеаризации ГХ ИП;

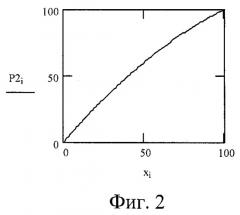
на фиг.2 - график ГХ ИП P₂(x), мВ;

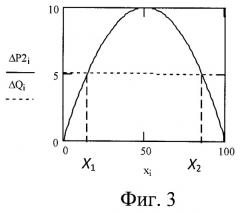
на фиг.3 - графики погрешности линейности ГХ ΔP₂(x), мВ, и прямой ΔQ(x), мВ, полученной от линеаризации ГХ по способу-прототипу;

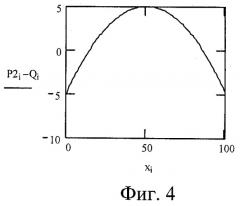
на фиг.4 - график погрешности линеаризации ГХ Р₂(x)-Q(x), мВ, по способу-прототипу;

на фиг.5 - графики погрешности линейности ГХ ΔР₂(x), мВ, и прямой ΔQL(x), мВ, полученной от линеаризации ГХ по заявляемому способу;

на фиг.6 - график погрешности линеаризации ГХ Р₂(x)-QL(x), мВ, по заявляемому способу.

Устройство состоит из источника эталонных напряжений (ИЭН) 1, измерительного преобразователя (ИП) 2, компьютера 3.

Изобретение осуществляют следующим образом.

В соответствии с заданным пределом погрешности аппроксимации (7) определяют коэффициент k=0,5 по формуле (5), где а=0 мВ, b=100 мВ, с=0,06, d=3 мВ. А по формулам (3), (4) определяют значения: x₁=8,377 мВ, x₂=78,474 мВ. Данные напряжения формируют в ИЭН 1. С выхода ИЭН 1 эталонные напряжения по очереди подаются на вход ИП 2. После преобразования в ИП 2 сигналы Р₂(x₁)=11,447 и Р₂(x₂)=85,231 поступают в компьютер 3, где регистрируются. По двум зарегистрированным сигналам Р₂(x₁), P₂(x₂) и значениям эталонных сигналов x₁, x₂, вычисленным в компьютере 3, в компьютере 3 определяется прямая QL(x):

линеаризующая ГХ с погрешностью P₂(x)-QL(x), мВ, представленной на фиг.6 и входящей в заданный предел погрешности аппроксимации.

Так как величина нелинейности ГХ современных ИП мала (фиг.2), то для оценки вида нелинейности лучше использовать характеристику погрешности линейности, вычисляемую как разность между ГХ Р₂(x) и прямой Р₁(x)=x, проходящей через края ГХ. Пример такой погрешности линейности ГХ ΔР₂(x)=P₂(x)-P₁(x), мВ, приведен на фиг.3. На данном чертеже представлена также прямая ΔQ(x)=Q(x)-Р₁(x)=5, мВ, где Q(x) - прямая, получаемая по способу-прототипу и делящая погрешность линейности ровно пополам (фиг.4). Максимальная погрешность линеаризации Р₂(x)-Q(x) в данном примере равна 5.

На фиг.5 показан график погрешности линейности ГХ ΔP₂(x), мВ, и график прямой ΔQL(x)=QL(x)-Р₁(x), мВ, где QL(x) - прямая (8), полученная от линеаризации ГХ по заявляемому способу.

Таким образом, формирование эталонных сигналов, значения которых зависят от задаваемого предела погрешности линеаризации и равны (3), (4), позволяет оптимально распределить погрешность линеаризации ГХ ИП по диапазону изменения измеряемой величины и тем самым обеспечить выполнение заданного требования по погрешности линеаризации ГХ. Например, использование способа-прототипа не позволило бы линеаризовать ГХ в виде полинома Р₂(x) с пределом абсолютной погрешности линеаризации (7): при х=0 в способе-прототипе погрешность линеаризации равна 5, а должна быть не более 3.

Способ линеаризации градуировочной характеристики измерительного преобразователя, аппроксимируемой полиномом второго порядка, заключающийся в формировании двух эталонных сигналов, последовательной подачи эталонных сигналов на вход измерительного преобразователя, регистрации выходных сигналов измерительного преобразователя, определении прямой по двум зарегистрированным выходным сигналам измерительных преобразователей и значениям эталонных сигналов, задании предела абсолютной погрешности линеаризации в виде значения, пропорционального измеряемой величине:Δ_a=d+cx,где Δ_а - предел абсолютной погрешности линеаризации, d и с - постоянные, х - измеряемая величина, отличающийся тем, что формируют значения эталонных сигналов зависящими от предела абсолютной погрешности линеаризации и равными: где x₁, x₂ - значения эталонных сигналов; а и b - нижняя и верхняя границы диапазона изменения измеряемой величины;